组合预测模型在股指期货定价上的运用

张 霞， 刘芃岍

1.安徽财经大学工商管理学院，蚌埠,2330030； 2.安徽财经大学数量经济研究所，蚌埠,2330030

组合预测模型在股指期货定价上的运用

张 霞1， 刘芃岍2

1.安徽财经大学工商管理学院，蚌埠,2330030； 2.安徽财经大学数量经济研究所，蚌埠,2330030

通过把不同类型的预测模型引进金融资产定价领域，从而使股指期货的定价更为精准，首先根据股指期货合约的市场价格与标的资产在股票市场的现货价格推算出隐含在市场价格中的除去资产收益率的无风险利率列，再对所选序列进行预测分析和拟合，运用三种单项预测模型方法，构建基于IGOWLA算子组合预测模型，用得出的结果进行股指期货的定价，然后通过所建立的评价指标来进行预测分析，研究表明在对金融资产定价时，运用组合预测模型比运用单项预测模型精准度更高。

对数灰色关联度；隐含除息无风险利率；IGOWLA算子；股指期货定价

1 相关理论与问题提出

当组合预测理念被Bates.J.M和Granger.C.W.J提出后，这个概念和方法就被很多学者应用于各个领域，并用具体实例来说明组合预测的结果比单项预测的结果更加合理和有效[1]。为了分析滑坡灾害，姚为利用组合预测模型来研究预测回声状态网络[2]；为了研究日本入华游客数量，章节宽利用组合预测方法进行预测分析[3]；为了预测铜的价格，王书平等构建多尺度组合预测模型进行预测[4]；为了分析2012-2015年商品房均价，杨桂元运用诱导有序加权调和平均(IOWHA)算子组合预测模型进行预测分析[5]。

同时，组合预测理论也在进一步的完善和发展，主要体现在对算子理论和误差理论的拓展上：Yager提出有序加权平均算子(OWA)[6]，陈华友建立了诱导有序加权平均算子(IOWA)的组合预测模型[7]，伍之前把从OWA算子推广的广义有序加权平均算子(GOWA)用于解决直觉模糊环境下的多属性决策问题[8]，刘兮用引入诱导值的IGOWA算子来解决二元语义多属性决策问题[9]，袁宏俊把取对数后的单项预测值再进行IGOWA算子运算，再将得到的IGOWLA算子进行区间组合预测模型的研究[10]。相比于其他学者对组合预测模型的算子与误差理论的探索，本文强调组合预测的实际运用，即根据期望的预测效果来选择算子和预测模型。

不管是开市时间还是闭市时间股票市场都比金融市场晚15分钟。对股指期货定价，要根据股票市场的收盘价格，同时为了提高定价的精准度，把组合预测模型和金融期货理论相结合。因为股票指数难以预测，所以本文对金融资产的定价主要依据对除息无风险利率的预测，观察预测值和实际值的终值，并计算两者之差，差距越小精准度越高。因此本文构建了新的组合预测模型——引入IGOWLA算子加权终值平均组合预测模型，从而使最终结果更加准确。

2 研究方法

2.1 股指期货定价[11]

定价需要用到的主要符号：

T表示股指期货合约的到期时刻，t表示股指期货合约到期前的某一时刻，S表示股指期货标的资产在t时期的价格，F表示t时刻股指期货合约的理论价格，r*表示T时刻到期以连续复利计算的t时刻的无风险年利率，Y表示每一笔交易的费率，rl与rb表示借入利率与借出利率，X表示卖空限制导致的成本比例，q表示标的资产在T-t时刻以连续复利计算的收益率。

股指期货理论价格F应满足：

1-XS1-Ye(rl-q)(T-t)

≤F≤S1+Ye(rb-q)(T-t)

X=0，Y=0，rl=rb=r*是完美市场时的理论价格。

2.2 隐含除息无风险利率

设期货价格满足公式F=Se(r*-q)(T-t)，则：

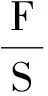
2.3 加权终值平均的组合预测模型

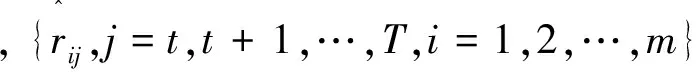
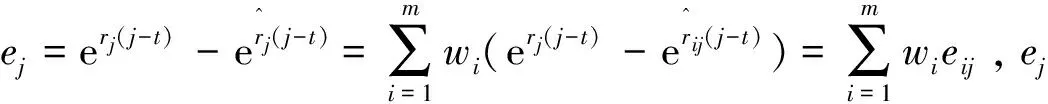
终值误差的组合预测模型可表示如下：

其中，W=(w1,w2,…,wm)是各种预测方法的加权系数向量，满足方程的W向量即终值误差组合预测模型的最优解。

2.4 IGOWLA算子[12]

fW(〈v1,a1〉,〈v2,a2〉,…,〈vm,am〉)

称fw函数是由v1,v2,…,vm所产生的的m维广义诱导有序加权对数平均算子，记为IGOWLA算子，vi是ai的诱导值。λ∈-，0∪0，+，v-index(i)是v1,v2,…,vm中按从大到小的顺序排列的第i个大的数的下标。

2.5 基于对数灰色关联度的IGOWLA组合预测模型

令：

其中，i=1,2,…,m；j=1,2,…,t,t+1,…,T，则ait表示第i种预测方法第j时的预测精度，这样m种单项预测方法第j时刻预测精度和其对应的在样本区间的预测值就构成了m个二维数组：

设W=(w1,w2,…,wn)T为各种预测方法在组合预测中的OWA的加权系数向量，将m种单项预测的方法第j时刻预测精度序列a1j,a2j,…,amj从大到小的顺序排列，设a-index(ij)是第i个大的预测精度的下标，则由精度预测序列a1j,a2j,…,amj所产生的IGOWLA组合预测值为：

令：

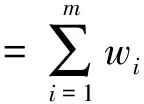
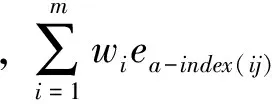
则基于灰色关联度的IGOWLA算子预测模型的数学表达式为：

3 实证分析

3.1 假 设

卖空成本等于交易费率等于零，借入资金利率等于借出资金利率。

3.2 数据来源

本文数据来源于WIND数据库。收集了数据库中2016年1月1日至2017年1月1日时间区间内沪深300指数的日收盘价数据以及IF股指期货的当月连续、下月连续、下季连续以及隔季连续的期货合约剔除到期日的日收盘价的数据。

3.3 实证分析

3.3.1 隐含除息无风险利率r的提取

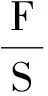
3.3.2 单位根检验联合F统计量[13]

运用单位根检验方法对这4种隐含除息无风险利率进行检验，非平稳的时间序列可以分为3种：不含时间项和漂移项的单位根非平稳序列、不含时间项带漂移项的单位根非平稳序列和既包含时间项又包含漂移项的单位根非平稳序列。

3.3.3 构建预测模型

根据隐含除息无风险收率的特征，选用自回归模型AR(p)、移动平均模型MA(q)以及ARIMA(p,i,q)模型，对4种隐含除息无风险利率序列进行拟合，依据偏自相关函数(PACF)识别AR(p)模型的阶数和Akaike信息准则来明确AR(p)的阶数，接着用Ljung-Box统计量来验证在5%的水平下，拟合模型的残差是否服从正态分布。通过自相关函数(ACF)来识别MA(q)模型的的阶数和Akaike信息准则来明确MA(q)的阶数，然后用Ljung-Box统计量来验证在5%的水平下，拟合模型的残差是否服从正态分布。按照推广的自相关函数(EACF)来识别ARIMA(p,i,q)模型的阶数和Akaike信息准则来明确ARIMA(p,i,q)阶数，然后用Ljung-Box统计量来验证在5%的水平下，拟合模型的残差是否服从正态分布。

表1 实际值与各单项预测方法预测值

根据表1的预测结果与实际结果的对比计算各个序列在各个时点处的预测精度，自回归模型AR(p)、移动平均模型MA(q)以及ARIMA(p,i,q)模型对4种隐含除息无风险利率序列进行预测的精度结果记为a1j、a2j和a3j所得精度序列结果见表2。

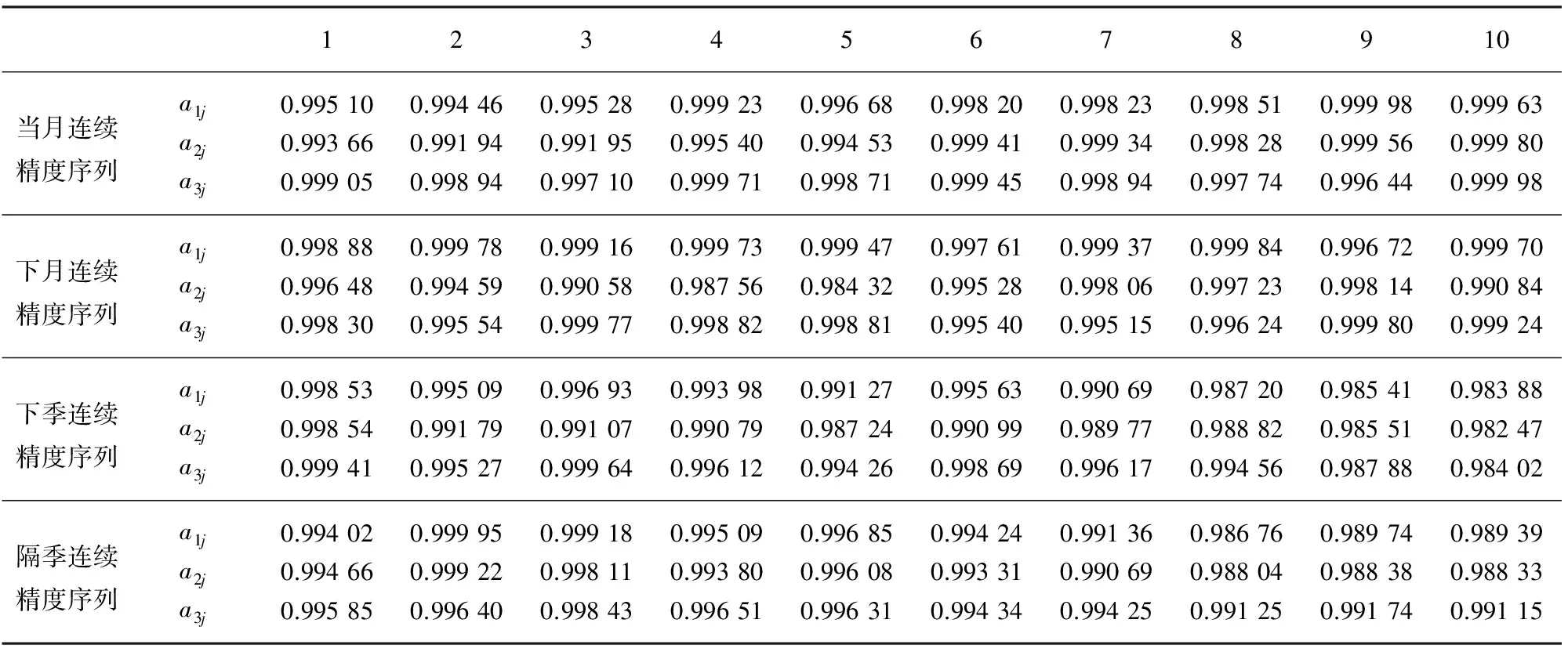
表2 各单项预测方法精度表

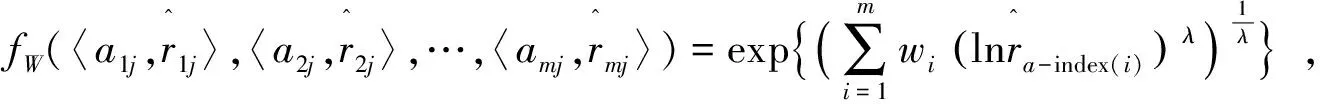
需要说明的是，本文中组合预测模型和传统预测模型是不一样的，在传统组合预测模型中，组合预测中某一个单项预测方法最优权重系数为1，而单项预测方法权重系数为0，即当权重系数等于0就是冗余预测方法。而本文在模型中加入了诱导值，当权重系数等于1时，组合预测值是这三种单项预测方法中预测值精度最高的一个值，其实也间接反映出同时低于或者同时高于实际值的情况较多，信息之间的互补性较差，而不是说明存在冗余预测方法，即使组合预测模型和传统预测模型得出权重系数为1其余为0的相同结果，但表达的实际意义却大不相同。

3.3.4 股指期货定价及定价效果评价

因为股票市场比期货市场早15分钟闭市，本文的预测基点是在倒数第10个交易日，要想对IF股指期货进行定价，可以依据隐含除息无风险利率值和沪深300指数的收盘价，根据金融期货定价公式Fj=Se(r*-q)(j-t)和先前的假设条件，4种期货合约是IF1701、IF1702、IF1703和IF1706，定价结果见表3。

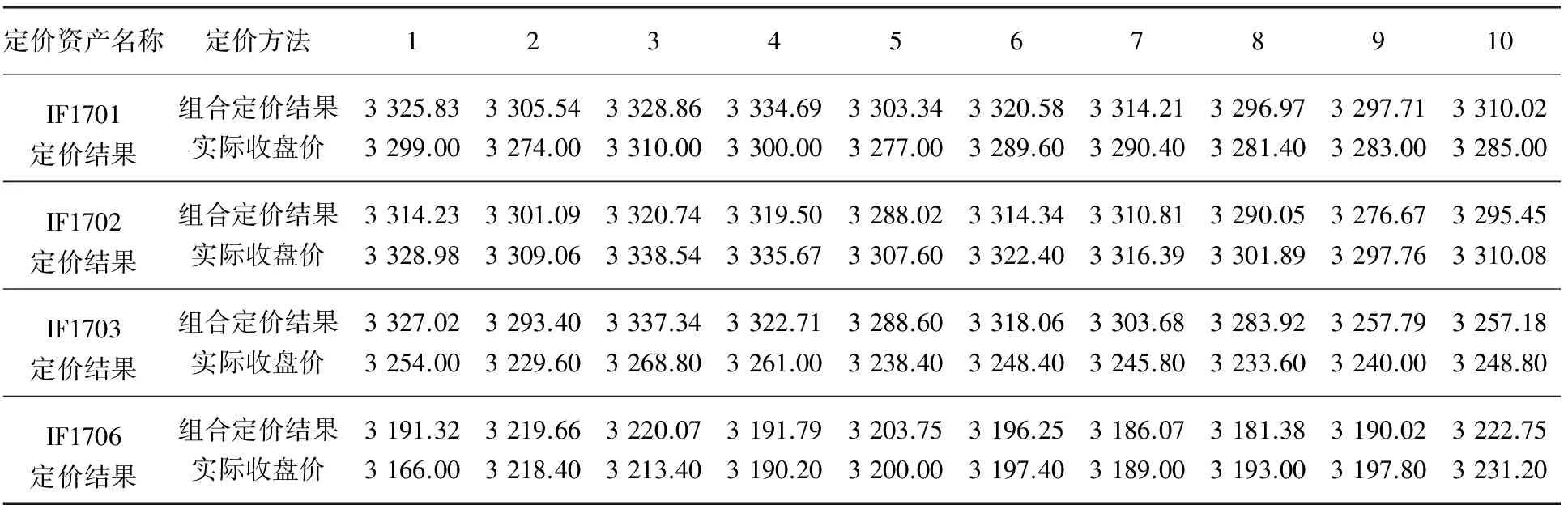
表3 IF股指期货组合定价结果

为了体现基于组合预测定价的有效性，可选用评价指标体系进行综合评价，通常选用的指标有平方和误差(SSE)、均方误差(MSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)以及均方百分比误差(MSPE)，数学表达式如下：

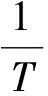
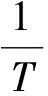
对于基于IGOWLA组合预测模型的股指期货定价结果评价见表4。

表4 预测效果评价指标体系

从表4的结果看，本文对股指期货定价所基于的带有灰色关联度的IGOWLA算子的组合预测模型的定价结果明显优于基于单项预测方法的定价结果，表明把组合预测模型引入金融资产定价理论中可以提高资产定价的精度。

4 结论与建议

本文对隐含在期货市场价格中的除息无风险利率进行了预测分析，构建了对数灰色关联度IGOWLA算子模型，依据模型预测出除息无风险利率，以用来对金融期货合约进行定价。结果表明：单项预测模型方法的精确度不如对数灰色关联度的IGOWLA预测模型方法。并且在时间数轴上，大多数时间上IF股指期货价格都比现货价格低，反映出市场对其产生悲观情绪，但是本文认为由于期货市场交易费用比较高和股票市场卖空成本这两个主要原因，导致现有的数据并不能反映真实的市场状况。要想使股指期货市场在风险管理和价格发现方面发挥作用，更好地进行风险管理和价格发现，本文提出以下建议：(1)股票市场可以通过允许股票做空取消融券限制，来降低股票市场的卖空成本。(2)可以使用更加宽幅的熔断机制来取代涨跌停机制。(3)可以通过减少对机构投资者的限制，实行T+0交易机制，以削减股票市场的交易成本。

[1]Bates J M,Granger C W J.Combination of forecasts[J].Operation Research Quarterly,1969,20(4):451-468

[2]姚为.滑坡灾害的回声状态网络组合预测[J].统计与决策,2014(19):73-76

[3]章杰宽.智能组合预测方法及其应用[J].中国管理科学,2014,22(3):26-33

[4]王书平,胡爱梅,吴振信.基于多尺度组合模型的铜价预测研究[J].中国管理科学,2014,22(8):21-28

[5]杨桂元,罗阳,高俊.我国房地产价格组合预测模型探讨[J].统计与决策,2014(12):17-20

[6]Yager R R.On ordered weighted averaging aggregation operators in multicriteria decision making[J].IEEE Transactions on Systems ,Man and Cybernetics,1988,18(1):183-190

[7]陈华友,刘春林.基于IOWA算子的组合预测方法[J].预测,2003,22(6):61-65

[8]伍之前,李登峰.基于GOWA算子的直觉模糊多属性决策方法[J].运筹与管理,2010,19(3):60-64

[9]刘兮,陈华友,周礼刚.基于T-GOWA和T-IGOWA算子的二元语义多属性决策方法[J].统计与决策,2011(21):22-26

[10]袁宏俊,钟梅,吴庆鹏.基于IGOWLA算子的区间组合预测模型[J].统计与决策,2016(14):22-25

[11]郑振龙.金融工程[M].北京：高等教育出版社,2003：125-131

[12]陈启明,陈华友.基于IOWA算子的两类准则下的最优组合预测模型及其应用[J].数理统计与管理,2013,32(5):847-853

[13]聂巧平,张晓峒.ADF单位根检验中联合检验F统计量研究[J].统计研究,2007,24(2):73-80

[14]储震,杨桂元,吴齐.基于灰关联度的IGOWLA算子中国楼市库存的预测分析[J].佳木斯大学学报:自然科学版,2016,34(4):599-602

[15]吴齐,杨桂元,储震.基于对数灰关联度的IGOWLA算子最优组合预测模型[J].淮阴师范学院学报:自然科学版,2016,15(2):114-119

(责任编辑：刘小阳)

F832.51

A

1673-2006(2017)09-0026-05

10.3969/j.issn.1673-2006.2017.09.007

2017-05-15

张霞(1995-)，女，安徽六安人，在读硕士研究生，研究方向：企业管理。