多目标优化算法求解导叶关闭规律问题
丁 蕊, 冯宪彬, 姚远峰, 金大博
多目标优化算法求解导叶关闭规律问题
丁 蕊1, 冯宪彬1, 姚远峰2, 金大博3
(1. 牡丹江师范学院,黑龙江牡丹江 157000;2. 东北林业大学,哈尔滨150000;3. 牡丹江水力发电总厂,黑龙江牡丹江 157000)
针对目前的单目标优化方法没有均衡考虑导叶关闭规律各目标分量的问题,综合考虑影响导叶关闭规律优劣的水击压力、机组转速和尾水管最大真空度这三个因素,将导叶关闭规律优化问题抽象为含有多个自变量和极值点的多目标优化问题,构建导叶关闭规律问题的多目标优化模型,并使用实数编码的遗传算法求解导叶关闭规律的多目标优化问题,遗传算法不依赖于问题的具体领域,具有很强的鲁棒性,实数编码的方式可以避免算法解码时的时间消耗,正交设计法生成的初始种群个体分布均匀,有助于维持种群的多样性。使用基于遗传算法的多目标优化方法求解导叶关闭规律问题,与遗传算法优化结果相对比,实验结果表示了本文所提算法的有效性。
水电站过渡过程;导叶关闭规律;多目标优化;遗传算法
0 前言
优化导叶关闭规律是解决水力过渡过程问题的措施之一。优化的导叶关闭规律,可以在不增加对电站投资的情况下,一定程度上延长机组使用寿命,增强机组运行的稳定性,确保电站安全运行。无论是对已建成使用的水电站,还是正在建设的水电站,对于导叶关闭方式的优化问题研究都具有重要的理论和现实意义。
传统的解析方法试验、计算工作量大且优化效果不稳定,难以大面积寻优。白家骢等[1]使用正交设计法优化导叶分段关闭规律的参数,优化效果能够满足基本的工程需要。牛文彬等[2]使用单纯型加速法求解导叶关闭规律优化问题,将对导叶关闭方式的求解问题转化为以导叶关闭分段数和各段折点坐标位置为优化目标的优化问题,对导叶关闭过程分段,找出最优导叶关闭分段数并确定各段折点的最优位置。舒胜晖等[3]将总关闭时间和关闭过程拐点对应的时间等作为优化对象,使用遗传算法优化导叶关闭规律问题。王煜等[4]也使用遗传算法求解最优导叶折线关闭规律,使用初选的初始种群和最优保留策略提高算法效率。高志芹等[5]构建了导叶关闭规律优化的数学模型,并将水电站过渡过程数值计算与自适应遗传算法结合起来。樊红刚等[6]研究导叶关闭规律的非线性评价函数及多工况下的关闭规律,与单工况优化结果相比,更能满足实际控制要求。
本文在文献[5-6]的基础上,综合考虑影响导叶关闭规律优劣的水击压力、机组转速和尾水管最大真空度这三大因素,构建导叶关闭规律问题的多目标优化模型,将导叶关闭规律优化问题抽象为含有多个自变量和极值点的多目标优化问题,采用实数编码和正交设计的初始种群方式,利用基于遗传算法的多目标优化方法求解导叶关闭规律的优化问题。
1 多目标优化基础知识
不失一般性的多目标优化问题的数学模型[7]可以表示为:
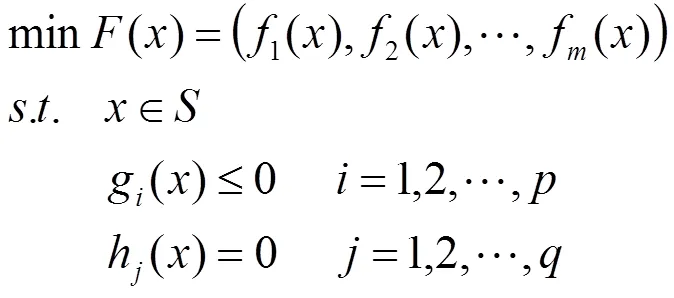
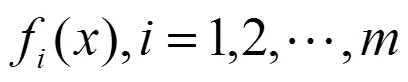
在多目标优化问题中,还有如下几个重要定义[8,9]:

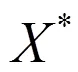
课前预习环节尽量放在在线学习平台上,利用微课传授基本知识,利用必读文字资源强化基础知识,利用选读资源拓展知识面,利用视频案例帮助学生理解和联系生活实际,利用Articulate等交互课件建构知识、参与讨论和分享。同时,教师还要对学生的网上活动进行及时回复和评价。在经过这样的课前预习后,学生不再空着脑袋来上课,而是带着储备、思考和问题来上课,具有明确的学习目标才能取得更好的学习效果。
定义5:Pareto前沿。是指Pareto最优解集中的解所对应的目标函数值在目标空间中形成的曲面。
由于多目标优化问题的多个目标之间常常存在冲突关系,即一个目标的优化是以牺牲其他目标为代价的,所以无法找到同时使所有目标都最优的解,只能寻找一个Pareto最优解集。
2 多目标优化算法求解导叶关闭规律问题
2.1 构建数学模型
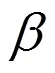


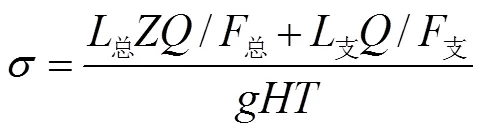
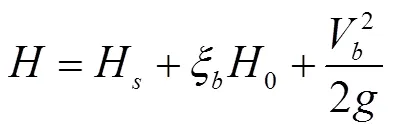

衡量导叶关闭规律优劣的多目标优化函数可简单描述为:

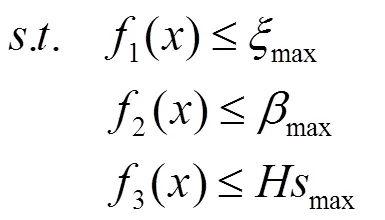

2.2 基于遗传算法的多目标优化算法
遗传算法作为一种较成熟的智能计算方法,因其具有自组织、自适应、高效率,不依赖具体问题和鲁棒性强等特点,成为求解复杂系统优化问题的通过方法,目前已广泛应用于生产实践中。使用基于遗传算法的多目标优化方法适于处理导叶关闭规律的优化问题。
2.2.1 算法流程
本文使用2.1节中构建的数学模型作为优化目标,具体的基于遗传算法的协同策略多目标优化算法如图1所示。
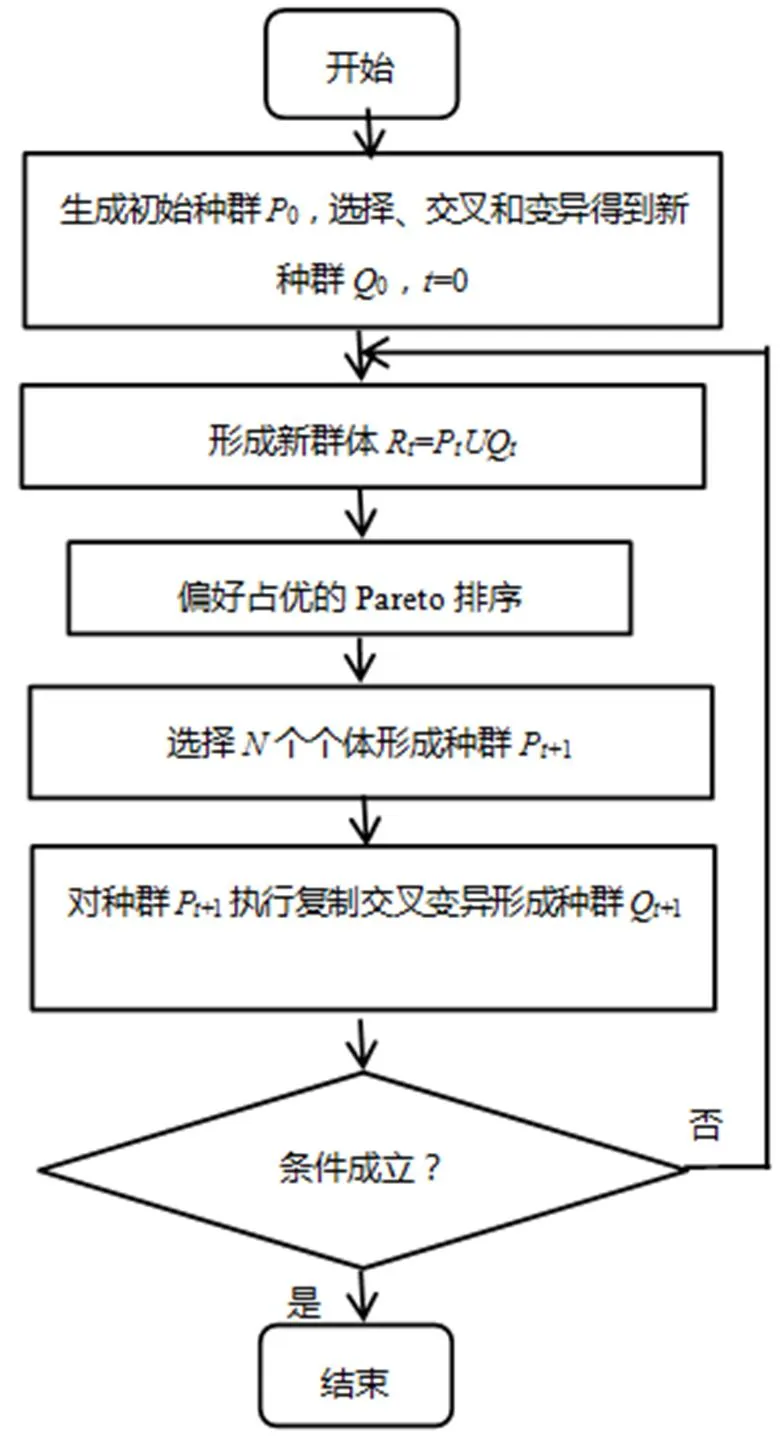
图1 基于遗传算法的多目标优化方法框架图
2.2.2 编码策略初始种群生成
本文使用实数编码方式,将设计方案映射为一个染色体,设计方案中的变量映射为染色体的基因,这种编码方式下的一个个体就代表一个设计方案。这种编码方式的优势是无需复杂的编码和解码,避免了复杂编码下降低算法搜索效率的问题。这里以导叶关闭规律中各折点所对应的时间和开度作为算法优化的对象,将时间和开度分别存放在两个一维数组中,且两者一一对应,即向量=[1,2,…,t]存放各折点时间,向量=[1,2,…,y]存放各折点的相对开度,算法中个体最终表示为=[,]。
2.2.3 初始种群生成
对于带约束的多目标优化问题,初始种群的生成方式对于算法的效率有一定影响。算法初始时种群中的个体如果能够满足约束需求,将能够提高算法的搜索效率。正交实验设计根据正交性从全面试验中挑选一些均匀分散的有代表性的数据进行试验,是一种高效的实验设计方法。由于本文中的个体是由时间和折点开度一一对应的实数向量组成的编码,可以使用正交设计的方式生成初始种群以提高算法的效率。这种初始种群生成的方式具有两个优势:一是均匀分散的个体使算法在初始时能够有相当好的种群多样性,二是能够避免因随机生成个体而导致的初始解不满足约束的情况。
3 仿真实验
实验主要验证多目标优化方法求解导叶关闭规律优化问题的优势。本文以某水电站为例,该电站总装机容量为62MW,额定流量为47.2m3/s,机组转动惯量为1000t·m2,额定转速214.3r/min,设计水头为35.5m,其他相关参数及计算公式详见参考文献[10]。目标函数的限制见表1。

表1 目标函数中涉及的限制值
机组采用折线关闭规律,根据工程实际情况,将导叶总关闭时间设置在0~9s的范围内,9s为过渡过程的计算总时间。将遗传算法和多目标优化方法求得的优化结果做对比,两种算法各运算10次,取平均值,其中多目标优化算法取10次算法运行获得的Pareto最优解集中解的平均值。

图2 导叶关闭规律折线示意图

表2 二种算法的各目标函数计算结果
表2是由遗传算法和多目标优化方法获到的相关参数值,图2是相对应的导叶关闭规律折线示意图。分析表2可知,与遗传算法相比较,使用多目标优化的方法求解导叶关闭规律,无需设定线性评价函数的权重系数,并且优化结果并不过度靠近控制边界,可以留有充分的安全余量,这是由于多目标优化方法求解的最优解能够均衡考虑各目标分量,在实际工程应用中,能够获得期望的安全余量较平均地分配到各单项极值中的最优解。
4 结语
本文综合考虑水击压力、机组转速、调压室最高涌浪、调压室最低涌浪和尾水管最大真空度这五大因素,将导叶关闭规律优化问题抽象为含有多个自变量和极值点的多目标优化问题,构建了导叶关闭规律问题的多目标优化模型,并使用实数编码的方式避免算法中解码时的时间消耗,正交设计法生成的初始种群方式使算法初始时个体分布均匀,多目标优化方法求解的导叶关闭规律最优解不仅能够快速找到稳定的优化结果,而且算法能够均衡考虑各目标分量,使安全余量能够较平均地分配到各单项极值中。使用基于遗传算法的多目标优化方法求解导叶关闭规律问题,实验结果表示了算法的有效性。
[1] 牛文彬, 杨丽娟. 水力机组调保计算导叶折线关闭方式优化研究[J]. 水力发电, 2004, 30(2): 54-57.
[2] 白家骢, 张莉芸. 用正交设计法优化导叶分段关闭规律的参数[J]. 大电机技术, 1995(4): 53-56.
[3] 舒胜晖, 樊红刚, 张保平,等. 遗传算法在抽水蓄能机组导叶关闭规律优化中的应用[J]. 清华大学学报(自然科学版), 2000, 40(11):35-38.
[4] 王煜, 田斌. 遗传算法在水轮机非固定模式导叶关闭规律中的应用[J]. 大电机技术, 2009(4): 42-47.
[5] 高志芹, 吴余生. 基于自适应遗传算法的水轮机导叶关闭规律优化计算[J]. 大电机技术, 2007(5): 32-36.
[6] 樊红刚, 崔赫辰, 陈乃祥. 导叶关闭规律非线性评价函数及多工况优化[J]. 排灌机械工程学报, 2013, 31(3):230-235.
[7] 陈深, 陈育成, 刘文胜. 基于Pareto最优的电力系统多目标优化研究[J]. 黑龙江电力, 2015, 37(1):32-37.
[8] 谢涛, 陈火旺, 康立山. 多目标优化的演化算法[J]. 计算机学报, 2003, 26(8):997-1003.
[9] 公茂果, 焦李成, 杨咚咚,等. 进化多目标优化算法研究[J]. 软件学报, 2009, 20(2):271-289.
[10] 司芹. 水电站水力过渡过程仿真分析与工程应用研究[D]. 南昌工程学院, 2015.
[11] 黄贤荣. 水电站过渡过程计算中的若干问题研究[D]. 河海大学, 2006.
Multi-objective Optimization Algorithm for Solving the Problem of Wicket-gate Closing Law
DING Rui1, FENG Xianbin1, YAO Yuanfeng2, JIN Dabo3,
(1. Mudanjiang Normal University, Mudanjiang 157000, China; 2. Northeast Forestry University, Harbin 150000, China; 3. Mudanjiang Hydropower Plant, Mudanjiang 157000, China)
Aiming at the problem of single objective optimization without considering the balance of each target component, considering the three factors--water hammer pressure, rotating speedand tail pipe maximum vacuum degreewhich have influence on the problem of wicket-gate closing law, the optimization problem of wicket-gate closing law can be abstracted as a multi-objective optimization problem with multiple variables and multiple extrema optimization problem. For solving the problem of wicked-gate closing law, the multi-objective optimization model is established, and real number encoding method is used. Using the multi objective optimization based on genetic algorithm to solve the problem of wicked-gate closing law, genetic algorithm does not depend on the specific field of problems, which has strong robustness. Real encoding method can be avoided decoding time consumption, which can save time. The orthogonal design method is used to make the individual distributing evenly, which is helpful to maintain the diversity of the population. Compared the results of multi-objective optimization with genetic algorithm’s, the experimental results show the effectiveness of the proposed algorithm.
transient process of hydro-power station; wicket-gate closing law; multi-objective optimization; genetic algorithm
TK370.2
A
1000-3983(2017)05-0072-04
牡丹江师范学院科研项目(1351MSYYB013)
2017-04-07
丁蕊(1977-),2009年毕业于哈尔滨师范大学,现从事计算机应用专业,硕士,讲师。


