E36船板钢动态再结晶行为研究
肖红亮 张慧杰
(1.湖南省国际工程咨询中心有限公司,湖南长沙 410016;2.湖南华菱湘潭钢铁有限公司材料研究所,湖南湘潭 411101)
E36船板钢动态再结晶行为研究
肖红亮1张慧杰2
(1.湖南省国际工程咨询中心有限公司,湖南长沙 410016;2.湖南华菱湘潭钢铁有限公司材料研究所,湖南湘潭 411101)
利用MMS- 200热模拟试验机对E36船板钢进行单道次压缩试验,研究了试验钢在变形温度850~1 100 ℃,应变速率为0.01~1 s-1条件下的动态再结晶行为。结果表明,E36船板钢在变形过程中发生了动态再结晶,且随着变形温度的升高和应变速率的降低,动态再结晶越易发生。通过计算得到的试验钢的变形激活能为373.78 kJ/mol,并由此建立了试验钢的本构方程及动态再结晶临界应变模型,为试验钢热变形工艺参数的制定提供了理论支持。
E36船板钢 动态再结晶 变形激活能 本构方程
E36船板钢具有较高的强度、良好的韧性以及优良的焊接性能。生产此类高性能船板钢时,必须采用控轧控冷工艺,通过控制热轧和轧后冷却过程中钢的相变过程,获得细小均匀的铁素体和珠光体组织[1]。因此了解奥氏体再结晶规律是合理制定E36船板钢控轧控冷工艺的基础。本文以E36船板钢为研究对象,通过研究流变应力与变形速率、变形温度等参数之间的关系,建立了E36船板钢的本构方程,并在此基础上确定了动态再结晶的临界应变值,为热加工工艺参数的制定提供理论依据。
1 试验材料和方法
试验采用工业生产的E36船板钢铸坯,其主要化学成分如表1所示。
将试验钢加工成φ8 mm×15 mm的圆柱体试样,在MMS- 200热模拟试验机上进行单道次压缩试验。具体工艺为:将试样以10 ℃/s 的速度加热到1 200 ℃保温5 min,然后以5 ℃/s 分别冷却到850、900、950、1 000、1 050和1 100 ℃保温30 s,再进行单道次压缩,变形量为60%,应变速率分别为0.01、0.1、1.0 s-1(如图1 所示)。

表1 试验钢的化学成分(质量分数)Table 1 Chemical composition of tested steel (mass fraction) %
2 试验结果与分析
2.1 试验钢的真应力- 真应变曲线
E36船板钢在不同应变速率(0.01、0.1、1.0 s-1),不同变形温度(850、900、950、1 000、1 050、1 100 ℃)下单道次压缩的真应力- 真应变曲线如图2所示。

图1 单道次压缩试验工艺示意图Fig.1 Schematic illustration of single- pass compression test

图2 试验钢在不同变形条件下的真应力- 真应变曲线Fig.2 True stress- true strain curves of tested steel under different deformation conditions
从图2可以看出,流变应力受变形温度及应变速率的影响较显著。E36船板钢在热压缩变形中出现了明显的动态回复与动态再结晶。随着变形速率的增加,材料可发生动态再结晶的下限温度不断升高。当应变速率为0.01 s-1时,发生动态再结晶的下限温度为900 ℃;应变速率为0.1 s-1时,其动态再结晶的下限温度为950 ℃;当应变速率增大到1 s-1时,试验钢发生动态再结晶的下限温度为1 050 ℃。且在相同的应变速率下,随着变形温度的升高,峰值应力逐渐降低,且峰值应力对应的应变也减小,说明越容易发生动态再结晶。这是由于变形温度越高,空位原子扩散和位错进行交滑移及攀移的驱动力越大,因此更容易发生动态再结晶[2]。
变形温度相同时,随着应变速率的增大,加工硬化能力越大,就越不容易发生动态软化,导致变形抗力逐渐增大。这是由于软化需要一个时间过程,应变速率较大时,晶粒没有足够的时间形核与长大;相反,当应变速率较低时,有足够的时间进行再结晶晶粒的形核与长大,即容易发生动态再结晶[3]。
2.2 峰值应力与变形条件之间的关系
峰值应力与变形温度、应变速率之间的关系如图3所示。从图3中可以看出,当应变速率相同时,随着变形温度的逐渐升高,峰值应力逐渐减小。在较高的变形温度下,动态软化能力较强,位错很容易通过滑移等方式消失。变形温度相同时,峰值应力随着应变速率的增大而增大,这主要是由于应变速率增大,加工硬化能力增强。
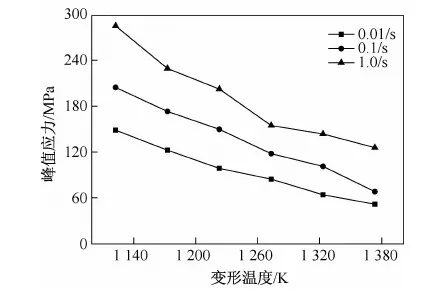
图3 峰值应力与变形温度、应变速率之间的关系Fig.3 Relationship among peak stress, deformation temperature and strain rate
2.3 热变形过程的本构方程
金属的塑性变形是一个热激活的过程。热变形的流变应力、应变速率和变形温度之间的关系可用包含变形激活能Q和变形温度T的双曲正弦函数[4-6]表示:
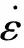
(1)
在低应力(ασ<0.8)时,式(1)可简化为:
(2)
在高应力(ασ>1.2)时,式(1)可简化为:
(3)
式中:α=β/n;n、β和A均为常数;Q为热变形激活能,kJ/mol,反映材料热变形的难易程度;R为气体常数,8.314 J/(mol·K);T为绝对温度,K;sinh为双曲正弦函数;σ为曲线的稳态流变应力或峰值应力,MPa。
对式(2)、式(3)两边分别取自然对数得:
(4)
(5)

从图4可以求出β=0.050 876 MPa- 1和n=6.527 642 521(具体数据见表2),进而可计算得出α=β/n= 0.007 794。

图4 不同变形温度下峰值应力σP与应变速率的关系Fig.4 Relationship between strain rate and peak stress at different deformation temperatures

表2 试验钢在不同变形温度下的应力指数n和βTable 2 Stress exponents of tested steel under different deformation temperatures
当应变速率一定时,对式(1)求导,可得ln[sinh(ασ)]-1/T的关系式式(6):
Q/(nR)={∂ln[sinh(ασ)]/∂(1/T)}
(6)
作ln[sinh(ασ)]-1/T的关系曲线见图5,该直线的斜率为Q/(nR),将R值和表2中计算得到的n值代入,可得0.01、0.1、1.0 s-1应变速率下的热变形激活能分别为415.41、352.97、352.97 kJ·mol-1。由此可知,E36船板钢的动态再结晶热变形激活能为373.78 kJ/mol。
对式(1)两边取对数可得:

(7)
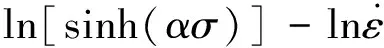
将上述计算得到的Q、n、α和A等材料常数值代入式(1),可得试验钢的热变形本构方程:
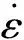
(8)
2.4 峰值应力与Z参数的关系
Z参数即Zener- Hollomon参数[7- 9],是表征温度补偿的应变速率因子,其表达式为:
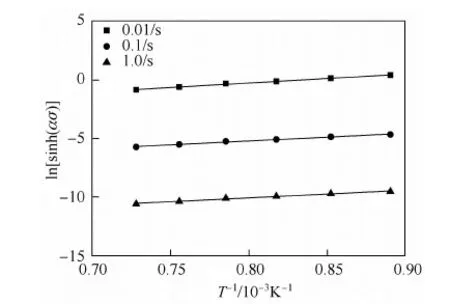
图5 不同应变速率下的ln[sinh(ασ)]-1/T关系图Fig.5 Relation of ln[sinh(ασ)]to 1/T at different strain rates

图6 不同变形温度下的关系图Fig.6 Relation of ln[sinh(ασ)] to ln at different deformation temperatures
(9)
将上述Q、A、α、n的结果代入式(9)可得:
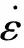
1032[sinh(0.007 794σ)]6.527 6
(10)
根据式(10)可得E36船板钢在不同变形温度与应变速率下的Z值,如表3所示。

表3 试验钢在不同变形温度及应变速率下的Z值Table 3 Z- values of tested steel at different temperatures and strain rates
根据以上计算结果,可将峰值应力σP用Z参数来表示:
=128.3×ln{[Z/2.979 44×1032]0.15+ [(Z/2.979 44×1032)0.31+1]0.5}
(11)
根据计算得出的Z值和式(11),可得峰值应力σP与Z参数之间的关系如图7所示。从图7可以看出,两者呈直线关系。

图7 试验钢峰值应力与Z参数之间的关系Fig.7 Relationship between peak stress and Z parameter for tested steel
2.5 动态再结晶的临界条件
临界应变量εc是判断材料是否发生动态再结晶的关键,只有当变形量大于临界应变量时,奥氏体才会发生动态再结晶。动态再结晶对应的临界应变量εc值在真应力- 真应变曲线上很难确定,而峰值应变εp比较容易确定,一般来说,奥氏体动态再结晶开始的临界应变εc和峰值应变εp之间存在如下关系[10- 11]:
εc=0.8εp
(12)

εp=A1Zm
(13)
对式(13)两边取自然对数可得:
lnεp=lnA1+mlnZ
(14)
由式(14)可以看出,lnεp与lnZ之间存在线性关系如图8所示,直线的斜率为m,截距为lnA1,回归可得m=0.215,A1=4.77×10-5。
将计算所得的m和A1值代入式(12)和式(13)可得:
εc=0.8εp=0.8×4.77×10-5Z0.215
=3.816×10-5Z0.215
(15)

图8 试验钢的lnεP与lnZ参数之间的关系Fig.8 Dependence of the critical stress for the initiation of DRX on Zener- Hollomon parameter for tested steel
根据以上关系式,可以预测E36船板钢在一定变形条件下发生动态再结晶的临界应变和峰值应变,可为热变形工艺参数的制定提供理论支持。
3 结论
(1)通过单道次压缩模拟试验,得到E36船板钢在温度850~1 100 ℃以应变速率0.01~1.0 s-1变形时容易发生动态再结晶。随着变形温度的升高和应变速率的降低,动态再结晶的临界应变量越小,峰值应力越小,动态再结晶越容易发生。

(3)计算获得了不同变形温度和应变速率下的Z参数值,并确立了峰值应力与Z参数的关系式为:σp=128.3×ln{[Z/2.979 44×1032]0.15+[(Z/2.979 44×1032)0.31+1]0.5}
(4)确立了动态再结晶临界应变εc与Z因子之间的关系式为:εc=3.816×10-5Z0.215,为试验钢热变形工艺参数的制定提供了理论支持。
[1] 程晓茹,任勇,张细菊,等.E36船板钢连续冷却转变行为研究[J].武汉科技大学学报,2008, 31(5):20- 24.
[2] 谭智林,向嵩. Q690低碳微合金钢热变形行为及动态再结晶的临界条件[J].材料热处理学报,2013,34(5): 42- 46.
[3] 赵英利.1 500 MPa级直接淬火马氏体钢的组织控制与强化机理研究[D].昆明:昆明理工大学,2010.
[4] MCQUEEN H J, YUE S, RYAN N D, et al. Hot working characteristics of steels in austenitics state[J]. Journal of Materials Processing Technology, 1995, 53(1/2): 293- 310.
[5] SHI H, MCLAREN A J, SELLARS C M, et al. Constitutive equations for high temperature flow stress of aluminum alloys[J]. Materials Science and Technology, 1997, 13(3): 210- 216.
[6] SELLARS C M, TEGART W J M. On the mechanism of hot deformation[J]. Acta Metallurgica, 1996, 14(9): 1136- 1138.
[7] ZENER C, HOLLOMON J H. Effect of strain- rate upon the plastic flow of steel[J]. Journal of Applied Physics, 1944, 15(1): 22- 27.
[8] RAO K P, HAWBOLT E B. Development of constituted relationship using compressing testing of a medium carbon steel[J]. Journal of Engineering Materials & Technology, 1992, 114(1):116- 123.
[9] JONAS J J, SELLERS C M, TEGART W J M. Strength and structure under hot working conditions[J]. Metallurgical Reviews,1969,14(1): 1- 24.
[10] KOMATSUBARA N, KUNISHIGE K, OKAGUCHI S, et al. Computer modeling for the prediction and control of mechanical properties in plate and sheet steel production[J]. The Sumitomo Search, 1990(44):159- 168.
[11] ROSSARD C. Mechanical and structural behaviour under hot working conditions[C]// Proc. 3rd Int Conf on Strength of Metals and Alloys. London: Institute of Metals, 1973:175- 203.
收修改稿日期:2016- 12- 28
ResearchonDynamicRecrystallizationBehaviorofE36ShipPlateSteel
Xiao Hongliang1Zhang Huijie2
(1.Hunan International Engineering Consulting Centre Co., Ltd., Changsha Hunan 410016, China; 2.Institute for Materials, Hunan Valin Xiangtan Iron and Steel Co., Ltd., Xiangtan Hunan 411101, China)
Dynamic recrystallization behavior of E36 ship plate steel was studied by means of single- pass compression tests on MMS- 200 thermo- simulation machine at temperature of 850 ℃ to 1 100 ℃ and strain rate of 0.01 s-1to 1.00 s-1. The results showed that dynamic recrystallization occurred for E36 ship plate steel during deformation, and higher deformation temperature and smaller strain rate rendered the dynamic recrystallization easier. The dynamic recrystallization activation energy of E36 steel calculated was 373.78 kJ/mol, and in view of the above the constitutive equation and dynamic recrystallization critical strain model was also set up, which could provide theoretical support for the development of hot deformation process parameters.
E36 ship plate steel,dynamic recrystallization,deformation activation energy,constitutive equation
肖红亮,男,博士,从事先进钢铁材料研究,电话:0731- 84442032,Email:hkw1123@163.com

