基于KKS模型Ni- Al合金γ′相粗化行为的三维相场研究

何 波 唐 尧 赵 彦 韦 华

(1.沈阳航空航天大学机电工程学院，辽宁沈阳 110136；2.上海大学材料科学与工程学院，上海 200444；3.中国科学院金属研究所高温合金研究部，辽宁沈阳 110016)

基于KKS模型Ni- Al合金γ′相粗化行为的三维相场研究

何 波1唐 尧1赵 彦2韦 华3

(1.沈阳航空航天大学机电工程学院，辽宁沈阳 110136；2.上海大学材料科学与工程学院，上海 200444；3.中国科学院金属研究所高温合金研究部，辽宁沈阳 110016)

基于CALPHAD热力学数据，采用KKS相场模型模拟了Ni- Al高温合金γ′相的三维析出行为。结果表明，γ′相粗化行为符合LSW理论结果，粗化动力学指数为3，粗化速率常数K=23.4 nm3/h，γ′相的体积分数为32%。弹性畸变能和有序畴的作用导致了γ′相颗粒的条状形貌和规则排列。

相场模型 Ni- Al合金 γ′相 粗化行为动力学

镍铝基高温合金因其优异的高温力学性能，被广泛用于航空发动机和工业燃气涡轮叶片等热端部件。该合金的组成相主要为无序fcc结构的γ基体相以及基体中共格析出的有序L12结构的γ′相。其中γ′相的体积分数可高达65%甚至更高，其尺寸、形状以及分布很大程度上影响了合金的强度、塑性、断裂韧性、蠕变、疲劳抗力等宏观性能[1]。因此，通过科学试验和理论模拟技术研究热处理过程中γ′相的析出行为始终是材料科学家关注的热点。

Hirata等[2]通过透射电镜(TEM)研究了γ′相的析出行为并计算了γ′相形核率；Xiao等[3]利用高分辨电子显微镜技术(HREM)研究了γ′相的早期析出沉淀行为；Babu等[4]研究了γ′相析出行为和过饱和γ基体相发生分解的过程。而通过计算机模拟方法，如有限元[5]、Monte Carlo[6]、相场法[7]等研究γ′相析出行为，可以对影响γ′相演化的因素和机制进行定量分析，并以此为依据来预测合金的组织形貌和性能的关联。这其中，相场法以序参量或物理参数表征微观组织构型，并引入体自由能、界面能、弹性能等来构建自由能泛函，通过求解相场方程可有效模拟复杂场条件下的微观组织演化行为，目前已被应用于枝晶生长[8]、有序间隙相的析出[9]、马氏体转变[10]和铁电畴演化[11]等的模拟中。

Kim (Kunsan National University, Korea)、Kim (Chongju University, Korea)和Toshio Suzuki(University of Tokyo, Japan)建立的KKS模型[12]是研究纳米至微米尺度γ′相析出行为的有效方法。该模型最早被用于凝固组织生长行为的模拟，由于固/液相界面和基体/沉淀相界面在关于序参量的设定上是相似的，物理上的合理性使其在固态相变中的应用[13]也获得了良好的效果。该模型的主要优势在于，为了适应真实的界面能，其界面宽度可以由双阱势高度来调整，从而允许选用较宽的界面以实现更大尺度的组织模拟。此外，KKS模型将界面考虑为成分不同而化学势相等的两相的混合，化学自由能函数为两相的吉布斯自由能，可以方便地将真实的材料热力学数据引入模型中。目前关于γ′相析出的相场模型研究主要集中在弹塑性力场的引入[14- 15]、多元合金体系的方程耦合[16]和高维空间的数值计算[17]等领域。近年来，程晓玲等[18]基于物理相场模型，通过耦合CALPHAD模拟了1 180 K温度下Ni- Al合金γ′相的二维析出过程，但三维模拟数据相对较少。

基于此，本文采用KKS相场模型，以及由CALPHAD获得的化学自由能和相关参数，对1 000 K温度下Ni- 18%Al(原子分数，下同)合金γ′析出相的形貌演化进行了三维模拟，获得了γ′相的形貌、体积分数和尺寸分布等特征变化，并通过讨论弹性畸变能和不同有序畴的影响，对有序相的析出、长大和粗化过程进行了探讨。

1 相场模型

相场模型求解n元体系的相变问题，需要引入n-1个守恒量(成分场变量)和一系列非守恒量(序参量)。本模型采用了1个成分场变量和4个序参量φi(r,t)(i=1, 2, 3, 4)。其中，(φ1,φ2,φ3,φ4)=(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)表示Ni- Al合金中γ′相的4种有序畴，(φ1,φ2,φ3,φ4)=(0,0,0,0)表示无序γ相。微观组织在时间t和空间r的演化，由描述保守场的Cahn- Hillard方程和描述非保守场的Ginzburg- Landau方程求解：

(1)

(2)

式中：M是溶质的化学迁移率，M=cAlcNi(cAlMNi+cNiMAl)，其中MNi和MAl从fcc相的Ni- Al原子迁移率数据库中获得[19]；L是序参量演化的动力学系数；系统的总自由能F可表示为：

(3)

式中：体积积分项代表体系的化学自由能，f(c,φi)为块体化学自由能，ε2为与界面能相关的梯度项系数，由于本文不考虑界面能各向异性，故取为常数；Eel为弹性能项。

式(3)中的块体化学自由能f(c,φi)是基体相和沉淀相的自由能的混合，以及剩余自由能密度、弹性能密度之和，可写成式(4)形式：

f(c,φi)=h(φi)fp(cp)+

[1-h(φi)]fm(cm)+wg(φi)

(4)

扩散界面区域是成分不同的沉淀相和基体相的混合，同时满足化学势相同：

c=h(φi)cp+[1-h(φi)]cm

(5)

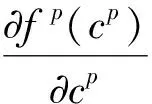
(6)

式中：cp和cm分别为组成界面区域成分c的沉淀相和基体相成分；fp(cp)和fm(cm)分别是沉淀相和基体相的吉布斯自由能，其表达式在给定温度下可以直接从CALPHAD数据库中获得[20]；h(φi)代表沉淀相的体积分数；wg(φi)为剩余自由能，w是双阱势高度。

φi+10)]

(7)

(8)

式中：α是与界面厚度有关的常数。通过式(7)和式(8)的分配，当序参量(φ1,φ2,φ3,φ4)=(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)和(0,0,0,0)时，体积自由能取极小值，式(4)分别等于有序相和基体相的自由能，式(5)等于沉淀相和基体相的成分浓度；当序参量的取值在0～1之间时，自由能和成分浓度为两相的混合，表示界面区域。

式(3)中的弹性能项Eel采用了均匀弹性模型[21]，以方便表示弹性能的大小：

(9)

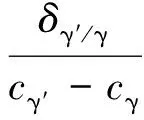
(10)

2 模拟结果与分析

图1为Ni- 18%Al合金在1 000 K温度下不同析出阶段的形貌演化模拟结果，对应的真实尺度为128 nm×128 nm×128 nm。图1(a)～图1(c)以Al元素的浓度表征了两相在三个互相垂直截面上的分布和形貌，其中蓝色区域表示基体γ相，红色区域表示沉淀γ′相，Al元素的浓度值如标尺所示。图1(d)～图1(f)显示了弥散分布的γ′相颗粒的三维形貌。从t=0.4 h到8 h，在γ′相颗粒平均半径增长的同时，颗粒总数减少了约3/4，整个过程中γ′相体积分数保持在32%左右。由于界面能和弹性能的作用，颗粒形状逐渐从球形转变为立方状、棒状，且分布沿[100]、[010]及[001]晶向排列。该转变大约发生在t=2 h后，颗粒平均半径为12 nm左右。

图1 Ni- 18%Al合金在1 000 K下的三维模拟结果Fig.1 3D simulation results of Ni- 18%Al alloy aged at 1 000 K

在沉淀早期，由于合金初始状态存在能量起伏、结构起伏和溶质起伏，体系趋于向总能量最小化状态推进，因而发生了溶质再分配，两相成分向各自的平衡浓度分化，过饱和的基体相溶质浓度降低，开始析出溶质浓度较高的γ′相。

随着两相成分在沉淀后期逐渐趋于稳定，溶质的扩散主要促使γ/γ′相界面不断推进，导致了γ′相的长大，局部γ′相的分解消失，相邻沉淀相的合并，γ′相的粗化和规则排列等一系列现象。如图1(a)～图1(c)中的A区域所示，在总自由能的驱动下，溶质从一个γ′相扩散到另一个γ′相，导致了前者的缩小消失和后者的长大；对于两个具有相同有序畴的γ′相，其界面区域相遇时，重叠界面的溶质浓度快速升高至γ′相平衡浓度，导致两个γ′相合并；由于弹性畸变能的存在，体系最优生长方向的溶质扩散速率最快，导致了γ′相的立方化，并影响了γ′相的合并和粗化的方向，最终使γ′相的形貌及排列分布具有明显的各向异性。

2.1 γ′相的粗化动力学及尺寸分布

经典的相粗化理论是由Lifshitz、Slyozov[23]和Wagner[24]在研究扩散控制的析出相粗化行为时提出的，简称为LSW理论。根据LSW理论，析出相的特征尺度随时间的演化满足：

(11)

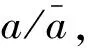
图2 1 000 K温度下Ni- 18%Al合金γ′相与时间t的关系Fig.2 -a as a function of t for γ′ precipitates of Ni- 18%Al alloy aged at 1 000 K

2.2 有序畴对γ′相粗化现象的影响

本研究中的三维相场模拟结果表明，γ′相的生长经历了形核、长大及粗化的过程，其中γ′相的粗化行为不仅与γ′相间距有关，还表现出了选择性粗化行为。如：有的γ′相间发生合并，而有些γ′相间未发生合并，这与实际合金的粗化行为具有相似性。本文模型中，γ′相通过序参量的定义具有4种有序畴，分别为(φ1,φ2,φ3,φ4)= (1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)。为此，下文通过两颗粒粗化行为来研究γ′相粗化过程中的相生长和界面行为。

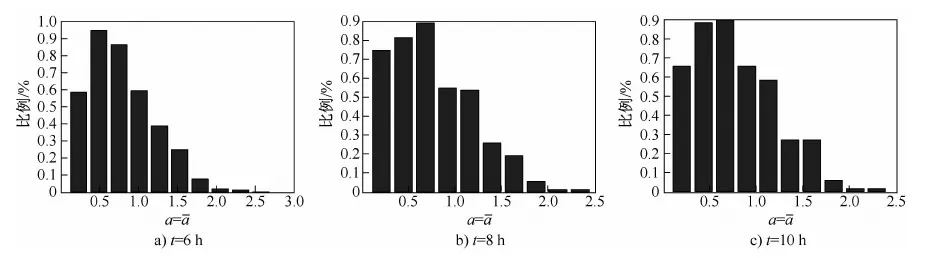
图3 粗化阶段三个不同时期γ′相的尺寸分布直方图Fig.3 Size distribution histograms of γ′ precipitates at three different stages during coarsening

图4模拟了1 000 K时，两个具有相同有序畴γ′相的粗化行为(见图4(a)～图4(d))及其成分随时间的演化(见图4(e))。在128×128计算区域上，设置两个圆形γ′相(见图4(a))，其半径分别为20和30个格点，中心相距54个格点，γ′相内部设置为平衡成分，基体γ相处于过饱和状态(cγ=14.78%Al)，两γ′相序参量设置相同，均为(φ1,φ2,φ3,φ4)= (1,0,0,0)。如图4所示，两个γ′相长大导致界面区域互相接触；在界面能驱动下，界面相连区域的溶质浓度逐渐升高至γ′相平衡浓度，γ′相间发生合并；同时由于弹性畸变能的作用，合并后的γ′相继续立方化导致条状γ′相的形成。

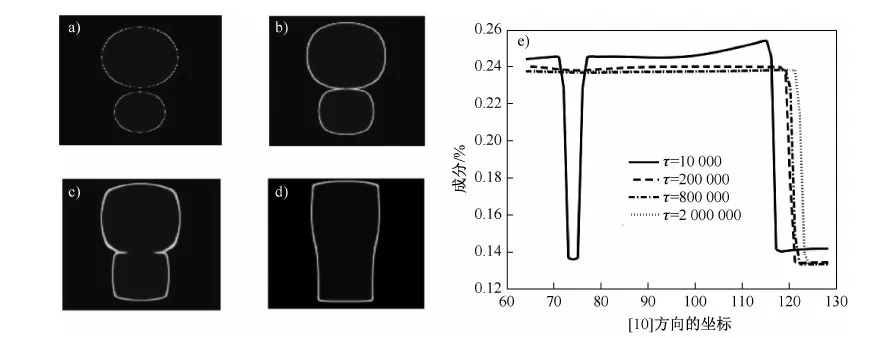
图4 相同有序畴间的γ′相的粗化(约化时间τ=10 000(a),200 000(b),800 000(c),2000 000(d))及对应时间的成分分布(e)Fig.4 Coarsening of γ' precipitates with same domain (reduced time τ=10 000 (a), 200 000(b),800 000 (c), 2 000 000(d)) and component distribution of the corresponding time (e)

与图4相对应，图5模拟了1 000 K时，两个具有不同有序畴γ′相的粗化行为(见图5(a)～5(d))及其成分随时间的演化(见图5(e))。其中，两个γ′相的序参量分别为(φ1,φ2,φ3,φ4)= (0,1,0,0)和(1,0,0,0)。由于界面区域存在一个比界面能更大的反相畴界能，两个γ′相在长大和立方化的过程中没有合并，但其界面区域先发生了连接(见图5(a)～5(b))而后又逐渐分离(见图5(b)～5(d))，反向畴界宽度增加。

该现象表明，三维相场模拟中的γ′相形核后，形成了序参量为(φ1,φ2,φ3,φ4)= (1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1) 4种类型的有序畴，相同的有序畴之间发生了合并而粗化，导致了棒状γ′相颗粒的产生；不同的有序畴之间界面在γ′相粗化过程中一直存在，使γ′相颗粒保持一定的尺寸，并形成相邻紧密排列的现象。

3 结论

(1)基于CALPHAD热力学数据，采用KKS相场模型对1 000 K温度下Ni- 18%Al合金γ′相的析出行为进行了三维模拟，模型中考虑了界面能和弹性畸变能的影响，根据模拟结果分析了形貌演化机制。

图5 两个不同有序畴的γ′相粗化(约化时间τ=10 000(a),200 000(b),800 000(c),2 000 000(d))及对应时间的成分分布(e)Fig.5 Coarsening of two γ' precipitates with different domains (reduced time τ=10 000(a), 200 000(b),800 000(c), 2 000 000(d)) and component distribution of the corresponding time (e)

(2)模拟的Ni- 18%Al合金γ′相的体积分数为32%，粗化动力学指数为3，粗化速率常数K=23.4 nm3/h，尺寸分布与LSW理论相近。

(3)利用两个不同大小的γ′相，分别模拟了相同有序畴间及不同有序畴间的γ′相的粗化行为。

[1] YU J J, SUN X F, ZHAO N R, et al. Effect of heat treatment on microstructure and stress rupture life of DD32 single crystal Ni- base superalloy [J].Materials Science and Engineering A, 2007, 460/461: 420- 427.

[2] HIRATA T, KIRWOOD D H. The prediction and measurement of precipitate number densities in a nickel- 6.05wt% aluminum alloy [J].Acta Metallurgica,1977, 25(12): 1425- 1432.

[3] XIAO S Q, HASSEN P. Herm investigation of homogeneous decomposition in Ni- 12at% Al alloy [J].Acta Metallurgica et Materialia,1991, 39(4): 651- 663.

[4] BABU S S, MILLER M K, VITEK J M. Characterization of the microstructure evolution in a nickel base superalloy during continuous cooling conditions [J].Acta Materialia,2001,49(20): 4149- 4160.

[5] OSAWA M, SHIRAISHI H, YOKOKAWA T, et al. 3D- FEM calculations of rafting in Ni- base superalloys based on high temperature elastic and lattice parameters[C]//Superalloys. Warrendale, PA: TMS, 2004: 977- 985.

[6] LEE J K. Coherency strain analyses via a discrete atom method [J]. Scripta Materialia Et Materialia, 1995, 32(4): 559- 564.

[7] WANG J C, OSAWA M, YOKOKAWA T, et al. Modeling the microstructural evolution of Ni- base superalloys by phase field method combined with CALPHAD and CVM [J]. Computational Materials Science, 2007, 39(4): 871- 879.

[8] PROVATAS N, GREENWOOD M, ATHREYA B, et al. Multiscale modeling of solidification: phase- field methods to adaptive mesh refinement [J]. International Journal of Modern Physics B, 2005, 19(31): 4525- 4565.

[9] RUBIN G, KHACHATURYAN A G.Three- dimensional model of precipitation of ordered intermetallics [J]. Acta Materialia,1999,47(7): 1995- 2002.

[10] YAMANAKA A, YOSHIHIRO T, TOMITA Y. Elastoplastic phase- field simulation of martensitic transformation with plastic deformation in polycrystal [J]. International Journal of Mechanical Sciences, 2010,52(2): 245- 250.

[11] CHOUDHURY S, LI Y L, LII C E K, et al. Phase- Field Simulation of Polarization Switching and Domain Evolution in Ferroelectric Polycrystals [J]. Acta Materialia, 2005, 53(20):5313- 5321.

[12] KIM S G, KIM W T, SUZUKI T. Phase- field model for binary alloys [J]. Physical Review E, 1999, 60 (6): 7186- 7196.

[13] ZHOU N, SHEN C, MILLS M, et al. Large- scale three- dimensional phase field simulation of γ′- rafting and creep deformation [J]. Philosophical Magazine, 2010, 90(1- 4): 405- 436.

[14] ZHOU N, SHEN C, MILLS M J, et al. Phase field modeling of channel dislocation activity and γ′ rafting in single crystal Ni- Al [J]. Acta Materialia, 2007, 55(16): 5369- 5381.

[15] RODNEY D, LE BOUNAR Y, FINEL D R A. Phase field methods and dislocations [J]. Acta Materialia, 2003, 51(1): 17- 30.

[16] KITASHIMA T, HARADA H.A new phase- field method for simulating γ′ precipitation in multicomponent nickel- base superalloys [J].Acta Materialia, 2009, 57(6): 2020- 2028.

[17] RUBIN G, KHACHATURYAN A G. Three- dimensional model of precipitation of ordered intermetallics [J]. Acta Materialia, 1999, 47(7): 1995- 2002.

[18] CHENG X L, LI Y S, ZHANG L, et al. Phase field simulation of morphology evolution and coarsening of γ′ intermetallic phase in Ni- Al alloy [J]. Materials Science and Technology, 2013, 29(3): 364- 369.

[20] WANG J C, OSAWA M, YOKOKAWA T, et al. Modeling the microstructural evolution of Ni- base superalloys by phase field method combined with CALPHAD and CVM [J]. Computational Materials Science, 2007, 39(4): 871- 879.

[21] WANG Y, KHACHATURYAN A. Effect of antiphase domains on shape and spatial arrangement of coherent ordered intermetallics[J]. Scripta Metallurgica ET Materialia, 1994, 31(10): 1425- 1430.

[22] KAMARA A B, ARDELL A J, WAGNER C N J. Lattice misfits in four binary Ni- Base γ/γ′ alloys at ambient and elevated temperatures [J]. Metallurgical and Materials Transactions A, 1996, 27(10): 2888- 2896.

[23] LIFSHITZ I M, SLYOZOV V V. The kinetics of precipitation from supersaturated solid solutions [J]. Journal of Physics and Chemistry of Solids, 1961, 19(1): 35- 50.

[24] WAGNER C. Theorie der alterung von niederschl?gen durch umlösen (Ostwald- reifung) [J]. Berichte der Bunsengesellschaft für physikalische Chemie, 1961, 65(7/8): 581- 591.

[25] 赵彦, 张洪宇, 韦华, 等. 相场法研究含第二相颗粒多晶体系的晶粒粗化标度律[J]. 金属学报, 2013, 49(8):981- 988.

收修改稿日期：2016- 12- 12

Three-dimensionPhaseFieldStudyforγ′CoarseninginNi-AlSuperalloybasedonKKSModel

He Bo1Tang Yao1Zhao Yan2Wei Hua3
(1. School of Mechano- electronic Engineering, Shenyang Aerospace University, Shenyang Liaoning 110136, China; 2.School of Materials Science and Engineering, Shanghai University, Shanghai 200444, China; 3. Institute of Metal Research, Chinese Academy of Sciences, Shenyang Liaoning 110016, China)

Based on the CALPHAD thermodynamics data, the KKS phase- field model was used to simulate the 3D separation behavior of γ′ phase in Ni- Al superalloy. The results showed that coarsening behavior of γ′ phase showed good agreement with the LSW theory result. The coarsening kinetic index was 3, the coarsening rate constantKwas 23.4 nm3/h, and the volume fraction of γ′ phase was 32%. The function of elastic energy and ordered domains resulted in the bar shape and regular array of γ′ precipitates.

phase- field model，Ni- Al alloy，γ′ phase，coarsening kinetics

国家自然科学基金项目(No.51371173)和辽宁省自然科学基金项目(No.2013024011)

何波，女，副教授，博士，主要研究方向为结构和材料的组织性能分析，电话：024- 89728683，Email：hebo1978@163.com

赵彦，男，讲师，博士，主要研究方向为金属材料微观组织的模拟，电话：021- 66135388，Email：zhaoyan8626@shu.edu.cn