自适应随机共振降噪下的结构模态参数识别

俞 波， 刘展鹏， 姜绍飞

(1. 福州大学土木工程学院， 福建 福州 350116； 2. 福州市城乡建设委员会， 福建 福州 350005)

自适应随机共振降噪下的结构模态参数识别

俞 波1, 2， 刘展鹏1， 姜绍飞1

(1. 福州大学土木工程学院， 福建 福州 350116； 2. 福州市城乡建设委员会， 福建 福州 350005)

针对强背景噪声下结构模态参数难识别以及传统自适应随机共振单参数优化的不足， 提出一种基于改进多粒子群协同优化算法的多参数同步优化的自适应随机共振方法, 结合利希尔伯特变换来识别出结构的模态参数. 该算法能够更快得到最佳随机共振系统结构参数， 自适应地实现非线性系统、 输入信号和噪声之间的最佳匹配， 削弱强背景噪声响应中的噪声， 提高响应的输出信噪比. 数值仿真和试验均表明， 该方法参数寻优效率高， 简单易行， 能够成功识别出强背景噪声下结构的模态参数.

自适应随机共振； 粒子群算法； 强噪声； 模态参数识别

0 引言

模态信息是反映结构的固有属性， 其变化往往能够反映结构的健康状态， 因此识别出结构的模态参数， 进而对结构的健康状况进行监控、 评估[1]. 很多实际工程结构， 特别是大型的土木工程结构， 在长期服役过程中由于受到外界环境及车辆等振动荷载的影响， 使得传统传感器监测的数据存在大量噪声， 且通常输入未知， 这使得利用传统模态识别方法识别模态时存在困难. 因此， 识别强噪声环境下工程结构模态参数对实际工程中结构的工作状态评价至关重要[2].

近十几年来， 模态参数识别方法在环境激励下得到了巨大的发展， 学者们研究了许多新的方法及理论并将其运用在实际工程当中， 这些方法后来都得到了有效的验证， 如Ibrahim时域法、 最小二乘复指数法、 时间序列法、 特征系统实现算法和随机子空间法[3], 而希尔伯特变换技术和小波变换是最具有代表性的. 采用经验模态分解方法(EMD)处理含有较大噪声、 模态阶数过多以及系统阻尼比相对较大的信号时， 噪声和模式混叠会对其得到的模式函数(IMF)产生较大的影响. 在工程应用中， 小波分析具有需要人为选择小波基以及假定阀值会对其分析结果产生影响以至于丢失有用信息等缺陷， 从而导致识别的模态参数与实际结构本身固有值相差大.

近来部分学者采用随机共振[4]来处理强噪声弱信号的问题. 随机共振理论在处理强噪声下的微弱信号检测方面独具优势， 在抑制噪声的同时也能够增加微弱信号的能量， 从而达到更好地处理微弱信号的目的， 且已经被用于图像处理、 信号处理、 机械故障诊断等诸多领域中[5]. 在研究随机共振的过程中， 面临如何快速地调整系统参数使其达到最佳匹配条件的难题， 同时在随机共振的参数调节过程中, 系统参数的值可能相差甚远. 另外由于系统的参数是由系统的响应速度与信噪比的关系确定的， 而响应速度频率难确定， 因此在不能确定信号的最高频率时确定系统参数有很大困难.

针对以上这些问题， 本研究提出一种改进的自适应随机共振算法， 结合希尔伯特变换技术， 实现了强噪声环境下的结构模态参数提取， 并通过一个简支梁的数值模拟和实验室试验验证该方法的可行性和有效性.

1 自适应随机共振原理

1.1 基本原理

随机共振是在某些非线性/线性系统中， 当信号和噪声产生协同作用， 部分噪声能量会转化为信号能量， 使系统输出的信噪比出现峰值， 类似于力学的共振现象. 产生随机共振需要非线性系统U(x,t)、 弱输入信号s(t)及噪声n(t)三者协调达到一定的匹配关系[6]. 传感器采集到的动力响应包含的噪声及振动信息都已经确定， 因此非线性系统的参数及算法选择十分重要， 研究中通常采用非线性双稳态系统, 动力学方程可以表示为[7]：

该系统描述的物理过程为处在势阱中的布朗粒子受到随机力n(t)和周期激励s(t)同时作用， 在过阻尼的极限条件下的演化运动过程， 其中U(x,t)双稳系统势函数， 表达式为：

其中：a、b为系统参数， 将式(2)带入式(1)， 可以得到布朗粒子的运动方程：

图1 双稳势阱图Fig.1 Diagram of bistable potential well

图1为双稳势阱图， 由图中可见， 当外界输入为零时， 根据系统运动方程， 就会存在两个相同的势阱点， 位于x=xn=(a/b)1/2和x=0处的势垒点，质点处于其中的一个势阱， 势垒高U=a2/4b. 当输入不为零， 系统将不再处于平衡状态， 势阱在外部激励的驱动下发生倾斜， 当噪声与周期力发生协同作用时， 势垒高将达到最小值， 弱信号受一定的噪声驱动在势阱间往复跃迁， 根据系统发生随机共振现象可以检测出强背景噪声下的弱信号.

1.2 存在的问题

由于受到绝热近似理论的限制， 传统的随机共振只适合于一些信号幅值、 信号频率、 噪声强度远小于1的小参数信号， 这对随机共振在工程实际中的应用产生了极大的制约作用. 同时， 在这种限制之下， 仅通过调节系统参数无法产生共振. 为了克服绝热近似理论对小参数的限制， 近年一些学者对其进行了相关的改进研究， 冷永刚等[8]提出二次采样随机共振方法， 即把大频率的周期信号移入噪声能量集中的低频区域， 同时将大频率信号转换为慢变低频信号.

针对传统自适应随机共振系统只对单一参数进行优化的缺点， 一些学者将优化算法引入随机共振系统进行结构参数的优化， 用于降噪处理以及增强信号有效成分. 例如： 遗传算法[9]、 粒子群算法[10]， 蚁群算法[11]等应用于随机共振系统结构参数的优化， 考虑了各个参数之间的交互作用， 实现了多参数的同步自适应选取. 但上述算法均没有充分利用非线性系统发生随机共振时系统的特性知识， 导致随机共振在微弱信号实时检测时未能充分发挥快速性优势. 粒子群算法是一种多变量全局优化方法， 效率高， 具有很强的工程实用价值. 针对非线性双稳态系统， 调节系统参数改变势垒， 使其与噪声强度大致相等， 系统会产生最佳共振效应. 将系统的这一特性作为知识， 融入到粒子群算法中来引导系统参数的优化， 以期提高算法参数寻优的效率. 因此， 利用粒子群算法的全局并行搜索能力， 以平均输出信噪比为适应度函数， 采用基于知识的粒子群算法来快速同步优化随机共振系统结构参数， 以实现淹没在强噪声中的微弱信号的自适应提取.

2 基于改进粒子群优化的自适应随机共振

2.1 改进粒子群优化算法

受鸟群觅食行为的启发， 1995年， Kenndy等[12]提出了粒子群优化算法. 随后， 考虑到标准粒子群优化算法容易陷入局部最优等问题， 许多学者在此基础上进行了改进. 其中， Zhang等[13]结合协同进化算法提出了多粒子群协同进化算法(MPSCO)， 该算法兼顾了种群的多样性和收敛速度， 使粒子陷入局部最优的可能性大大降低， 从而受到广泛的关注[14]. 然而， MPSCO在各层以同等效率进行优化计算， 仍然存在着陷入局部最优的可能性， 因此有些改进算法尽管能够在一定程度上提高算法的性能[15-16]， 同时却也使算法的复杂性增加了， 为此研究引入IMPSCO方法[17]， 即在引入协同进化算法时同时考虑权重系数， 将陷入局部最优粒子进行最差粒子替换， 从而进一步改善粒子群算法的寻优质量和稳定性. 算法的具体步骤如下： 每个粒子用一个D维的搜索空间代表， 即Pi=(pi1,pi2, … ,piD)， 粒子的速度表示为Vi=(vi1,vi2, …,viD)； 每个粒子调整自身策略飞向自身搜索到的最优位置pbestij和全局最优位置gbestij， 通过个体最优位置和全局最优位置的不断更新搜索最优解[18]. 惯性权重因子的位置和速度遵从以下公式更新：

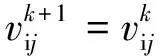
其中：r1、r2为[0, 1]间随机数；c1、c2为学习因子， 分别反应个体的认知学习和社会学习， 即个体探索能力和群体搜索能力， 当c1=c2=2.0且采用在[0.4, 0.9]之间线性变化的惯性权重时， 算法的识别性能一般较好.

IMPSCO算法的改进原理源于生物学中“自然选择”的思想： 在自然界中， 因为环境发生变化， 一些物种会消失， 同时也会有一些新物种出现， 以此保持物种的多样性， 这是自然选择的过程. 若假设粒子在解空间的寻优过程为物种在生物界自然选择的过程， 则当某个粒子多次被标记为最差粒子时， 就说明这个粒子的适应度低， 需要被淘汰， 同时需要产生一些适应度高的新粒子以保证种群多样性， 于是在IMPSCO算法中， 采用整个种群优良粒子的重心来替换那些需要淘汰的粒子.

2.2 适应度函数建立

粒子群算法在优化结果的好坏取决于各个粒子的好坏， 即建立适当的目标优化函数成为了关键. 合理的评价指标往往能够很好地反映优化结果. 研究选用随机共振的输出信噪比作为IMPSCO算法的适应度函数. 随机共振输出信噪比定义：

式中：f0、f1为信号频率和噪声频率；S(f0)、N(f1)分别为信号功率和噪声功率；P为系统总功率.

在响应采集中， 假设大参数信号输入频率为f0， 经过采样频率fS采样后得到矢量长度为l的离散序列Zl，Zl经过二次采样fsr后得到的信号频率为f=f0×fsr/fS. 信号经过离散后的模值为|X(k)|， 那么公式可以改为：

2.3 基于IMPSCO的自适应随机共振算法流程

基于IMPSCO的自适应随机共振算法具体流程如下：

① 初始化种群. 随机产生m个大小为n的子种群， 并将其分为上下两层.

② 适应度函数确定. 将传感器采集到的结构测量响应Π(t)经过二次采样， 实现响应从高频到低频的转换， 随后输入至随机共振系统， 采用式(1)～(3)计算出输入测量响应所对应的随机共振输出. 根据输出信噪比式(7)建立以随机共振输出信噪比为适应度的函数.

③ 适应度值计算. 将各子种群中所有粒子的位置及其所对应的适应度值存储为pbest(个体)和pbestval(个体极值).

④ 粒子更新. 分别按照式(4)～(5)来更新上层子种群和下层子种群， 并对整个种群中的最差粒子进行标记.

图2 自适应随机共振流程Fig.2 Process schematic diagram of adaptive stochastic resonance

⑤ 最优值更新. 重新计算更新后各粒子的适应度值， 然后将其与历史最优值进行比较， 如果适应度值更高， 则相应更新pbest、 pbestval、 gbest、 gbestval、 gbesti和gbestvali.

⑥ 最差粒子替换. 将粒子的最差标记次数与预先设定好的最差次数限值Lw进行比较， 如果等于Lw， 则按上述将其替换为选定优良粒子的局部重心Zgrav， 并将其最差标记次数归零.

式中:S和zj分别为选定优良粒子的数量和位置.

⑦ 判断是否达到了预设的最大迭代次数Imax或者达到最小误差， 如果没有则返回④， 反之则停止迭代并将搜索到的最优解结构参数a、b输出.

⑧ 将最优结构参数a、b输入非线性双稳系统中， 从而确定经过随机共振去噪后达到最佳信噪比的结构响应.

具体的流程如图2所示.

3 数值试验

3.1 结构模型

为了验证IMPSCO自适应随机共振的有效性， 采用Matlab建立一个钢简支梁模型对其进行验证. 模型的主要信息见表1. 模型共划分为40个单元， 单元长度25 mm, 见图3.

表1 模型的主要信息

图3 构件立体模型Fig.3 Structural model

3.2 处理结果与对比

在梁的21/40处施加一竖向向下的简谐荷载激励， 作用时间为5 s， 采用Newmark积分法计算结构响应， 系数γ=1/2，β=1/4， 响应信号采用加速度信号. 为模拟实际的动力加速度采集环境， 对模拟的加速度均添加噪声， 模拟采用高斯白噪声， 各测点添加方法见下式.

其中：yi是噪声污染后的加速度；yia是理论计算加速度；R是均值为0， 偏差为1的正态分布随机数；ε是噪声程度.

在无噪声情况下， 采用Newmark逐步积分法计算简支梁的加速度响应， 结果见图4(a)， 根据公式(9)， 往加速度响应值中添加60%水平的噪声， 结果见图4(b). 由图4可知， 在简谐激励作用下， 加速度响应也为一条简谐曲线， 对比可发现在60%水平的噪声环境下， 结构加速度响应完全被湮灭于噪声中， 无法从中得到所需要的相关信息.

图4 结构加速度响应Fig.4 Structural acceleration responses

利用自适应随机共振处理强噪声下的加速度响应, 经过试算， 采用表2所示的优化参数设置， 得到结果如图5所示.

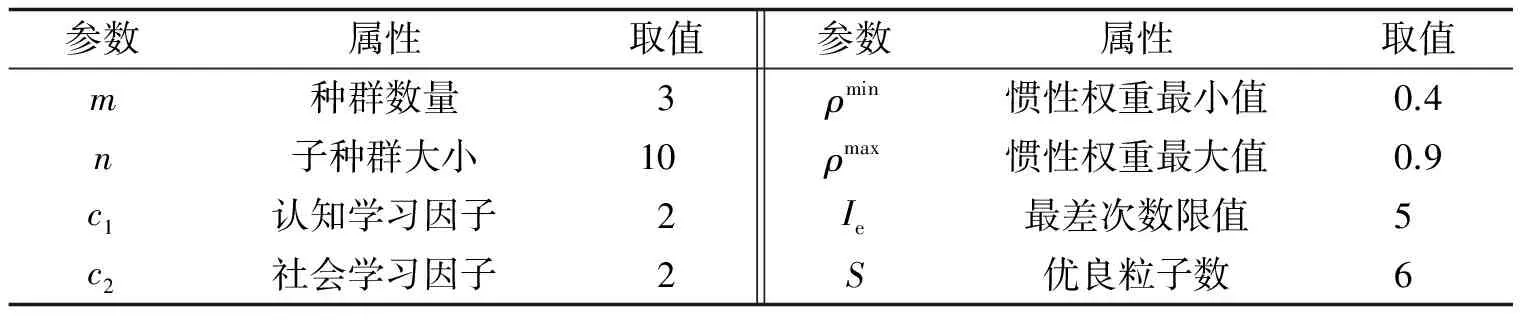
表2 IMPSCP参数设置

图5 随机共振处理后加速度响应Fig.5 Acceleration responses after stochastic resonance processing

由图5(a)迭代曲线可知， 经过迭代之后响应输出的信噪比达到最优值， 此时随机共振系统参数值为a=0.05，b=0.006，h=0.645. 将参数代回原双稳态共振模型中， 计算输出的波形如图5(b)所示. 图5(a)中， 随机共振输出信噪比由原来的4.43 dB增加到了26.45 dB， 增加了5.97倍； 输出的加速度响应幅值由原来的0.8增加至5.2， 增加了6.5倍， 此时结构加速度响应已从低信噪比转为高信噪比， 响应中的噪声被大量削除了. 对比图4(b)与图5(b)， 随机共振处理后的结构响应， 噪声很大程度被削除了， 输出响应的波形图与原波形图类似， 说明随机共振在降噪的时候并未丢失结构的相关信息.

数值仿真结果表明， 将粒子群算法应用于随机共振， 能实现双稳态系统参数的自适应求解， 可快速、 有效地增强强噪声背景下的结构响应的相关值. 为了进一步验证该方法的有效性， 将其与小波/小波包分析等降噪方法进行对比， 图6是小波/小波包处理后的加速度响应图.

图6 利用小波/小波包分析降噪后的加速度Fig.6 Acceleration responses after denoising by the wavelet analysis and wavelet packet

对比图5、 6的时域波形可以看出， 小波降噪得到的波形图比原始信号的幅值降低较多， 原因可能是在假定阈值时， 部分有用结构信息也被设定在了阈值内， 从而在去除噪声的时候将部分有用信息去除， 造成有用信息丢失， 且随机共振在一定程度上也去除了部分噪声. 但是从时域波形中可以看出， 信号的幅值大大增加， 可以理解为噪声将一定的能量转移给了有用信号， 从而增强了信号. 直接利用小波降噪的效果并不理想， 时域波形严重失真.

信噪比与噪声程度转化公式为

其中：Ps、Vs分别为信号的功率和电压幅值；Pn、Vn分别为噪声的功率和电压幅值.

根据式(10)可知， 加入60%的噪声与信噪比为4.43 dB的作用效果同等. 根据式(10)计算自适应随机共振、 小波降噪和小波包降噪3种技术所处理后的信噪比见表3， 从表3中可以看出， 在提高信噪比方面自适应随机共振的方法优于小波/小波包分析方法， 能够更好地提高响应信噪比从而减少噪声的干扰. 经过自适应随机工共振处理后， 强噪声下的最优结构响应被提取出来， 之后运用希尔伯特变换技术识别出3种降噪技术处理后所对应的结构的模态频率， 识别结果如表4所示. 从表4中可以看出， 经过随机共振处理后的结构响应所提取出来的模态频率值与理论值更加接近， 识别值优于小波/小波包分析方法.

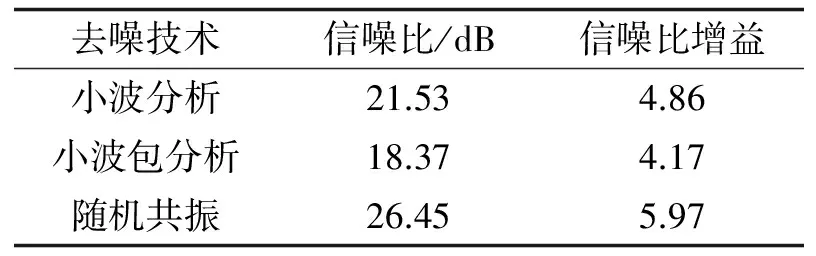
表3 对比各方法降噪后的信噪比

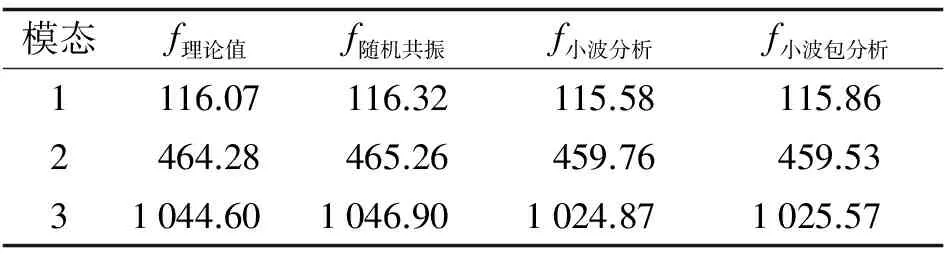
表4 模态频率识别值比较

4 简支梁试验验证

4.1 结构模型

试验结构模型为一个槽钢简支梁， 长度3.6 m， 模型截面面积A=6.99×10-4m2, 惯性矩I=1.15×10-7m4, 弹性模量E=206 GPa， 密度ρ=7 850 kg·m-3. 试验的响应采集如图7所示， 简支梁上布置7个传感器， 传感器布置位置如图7(a)， 不处于低阶振型节点. 试验采用瞬态锤击激励， 每一次激励输入后待加速度响应基本平稳且近似0值后才开始下一次激励， 但采样过程不中断.

图7 结构响应采集过程Fig.7 Acquisition processing of structural responses

4.2 结果与分析4.2.1 加速度响应对比

试验共进行两次， 第一次是在实验室无其他干扰环境下进行的， 此时仅有力锤自身敲击发出的声音， 可认为采集到的数据为无背景噪声情况下的结构加速度响应， 如图8(a)所示， 并计算此时结构响应功率， 记为E1； 另一次试验时试验室中相关的仪器如振动台、 MTS液压机同时运作发出声音， 吊车移动和力锤自身运作也发出声音， 外加当时下着雨， 可将这些干扰噪声定义为背景环境噪声， 此环境下采集到的结构加速度响应如图8(b)所示， 并计算此时结构响应功率， 记为E.

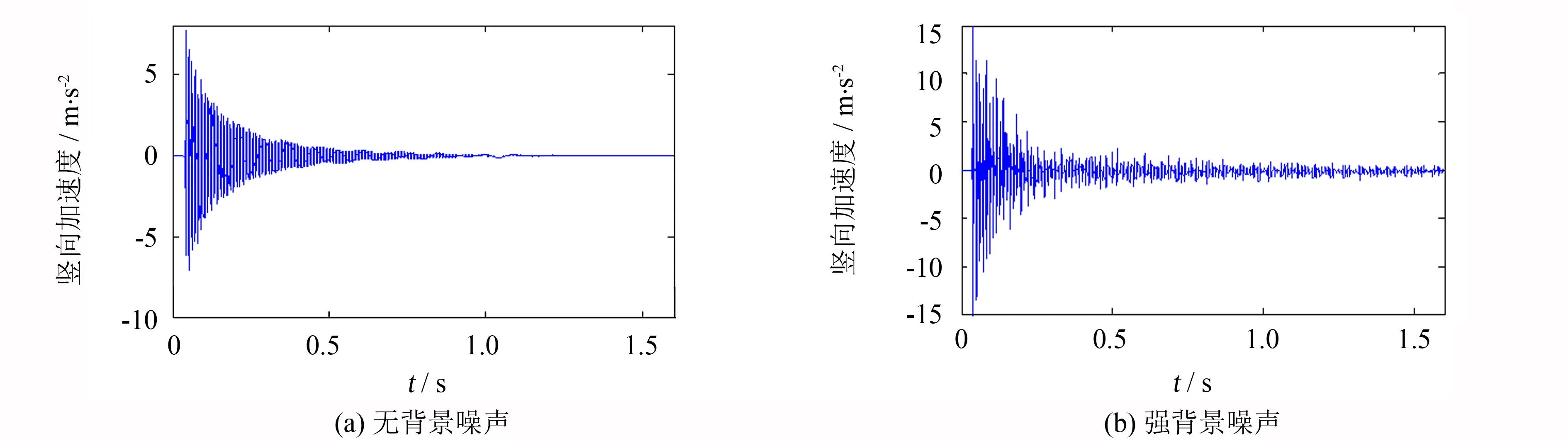
图8 试验钢梁加速度响应Fig.8 Acceleration responses of test beam

由于实测响应中噪声跟信号是混淆的， 无法确定响应的信噪比， 此时采用另外一种方式计算， 结合式(10)及计算所得的结构响应功率值， 可将信噪比公式转为如下式所示:

式中：E，E1为背景噪声采集到的结构响应能量和无背景噪声结构响应能量；N为噪声能量.

利用自适应随机共振处理强背景噪声下的加速度响应. 参数设置同3.2节； 此时寻优得到的共振系统参数值为a=0.004 2，b=0.005，h=0.85， 将其代回原随机共振系统中可得到输出的结构响应如图9所示.

图9 经随机共振处理后的加速度Fig.9 Acceleration after stochastic resonance

类似地， 分别采用小波/小波包对加速度响应进行处理， 结果如图10所示. 按照式(11)计算3种方法处理后的结构响应信噪比值， 如表5所示.

从图9、 10可以看出， 随机共振处理后的结构加速度响应在波形图上与原激励更加对应， 而且幅值也增大了从表5也可看出， 随机共振处理后的信噪比增幅大于小波/小波包分析， 这表明采用自适应随机共振响应处理方法去除噪声保留结构信息的效果较优.

表5各方法降噪后的信噪比对比

Tab. Comparison of SNR by different denoising methods

去噪技术信噪比/dB小波分析9．809小波包分析10．122随机共振12．360

图10 小波/小波包分析去噪Fig.10 Wavelet/wavelet packet analysis denoising

4.2.2 频率值对比

对频域方面的信息进行对比， 运用傅里叶变换分析3种方法处理后结构响应所对应的FFT频谱图如图11所示. 从图11 (b) 中可以看出强噪声的频率值已经不明显， 傅里叶变换后只能得到结构的第2、 第4阶频率值； 而经过小波/小波包降低噪后， 运用傅里叶变换得到的频率值也不能反映结构的真实频率值， 均不同程度出现了误识别， 如图11 (c)、 (d)所示； 通过随机共振处理后所得到的频率值如图11(e)所示， 可以看出随机共振处理后的频率值与理论值基本相符， 同时频谱图的幅值较11(a)图增加了将近10倍， 这表明经过随机共振处理后的强噪声结构响应， 傅里叶变换能够更好地提取结构的固有频率. 再利用希尔伯特变换技术识别出3种降噪技术处理后所对应的结构频率值， 如表6所示. 识别结果表明， 随机共振处理后的结构响应所得到的频率值与结构真实频率值更接近.

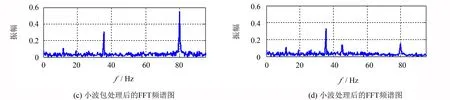
图11 不同技术频响函数对比Fig.11 Comparison of different frequency response functions

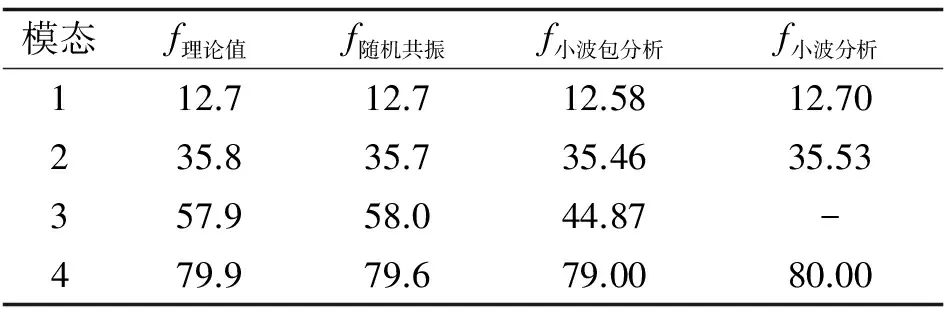
表6 模态频率识别值比较

5 结语

提出一种改进PSO的自适应随机共振算法， 通过利用PSO算法自身的优化能力， 能够自适应地确定随机共振系统参数， 结合希尔伯特变换技术识别出随机共振处理后响应所得到的模态参数， 得出以下结论.

1) 随机共振的匹配条件较难用数字化的方法确定， 由于土木工程结构的特殊性， 传感器采集到的振动信息包括噪声和信息， 所以如何确定随机共振系统的参数十分关键， 自适应随机共振算法具有自适应运算效率高、 不需要人为调整随机共振系统参数、 节省计算时间的优点.

2) 提出改进的PSO自适应随机共振算法是一种智能优化方法， 在强背景噪声下能够从时域波形中提取方法的有效性反应， 算法的效果优于常用的小波/小波包分析去噪技术， 通过该算法可以避免因直接滤除噪声而丢失有用结构信息， 后处理所识别出的结构模态频率值较精确， 对强环境噪声下的结构异常识别具有重要意义.

[1] 严平, 李胡生, 葛继平. 基于模态应变能和小波变换的结构损伤识别研究[J]. 振动与冲击, 2012, 31(1): 121-126.

[2] 杨佑发， 程亚鹏, 李华新. 环境激励下基于经验模式分解的结构模态参数识别方法[J]. 土木工程学报, 2013(增刊2)： 73-78.

[3] 续秀忠, 华宏星. 基于环境激励的模态参数辨识方法综述[J]. 振动与冲击, 2002, 21(3): 1-5.

[4] 陈敏， 胡茑庆， 秦国军. 参数调节随机共振在机械系统早期故障检测中的应用[J]. 机械工程学报， 2009， 45(4)： 131-135．

[5] 祝恒江, 李蓉, 温孝东. 利用随机共振在强噪声下提取信息信号[J]. 物理学报, 2003, 52(10): 2 404-2 408.

[6] 沈清华, 陈伟宏, 姜绍飞, 等. 随机共振结合RobustICA的两阶段结构损伤定位方法[J]. 福州大学学报(自然科学版), 2014, 42(6): 916-922.

[7] 赵文礼， 刘进， 殷园平． 基于随机共振原理的中低频信号检测方法与电路设计[J]． 仪器仪表学报， 2011， 32(4)： 721-728．

[8] 冷永刚， 王太勇， 郭焱． 二次采样随机共振的工程应用研究[J]． 中国机械工程, 2004， 15(20): 1 847-1 852．

[9] 李戈, 秦权, 董聪. 用遗传算法选择悬索桥监测系统中传感器的最优布点[J]. 工程力学, 2000, 17(1): 25-34.

[10] 李继猛， 陈雪峰， 何正嘉． 采用粒子群算法的冲击信号自适应单稳态随机共振检测方法[J]. 机械工程学报， 2011， 47(21)： 58-63．

[11] 雷亚国， 韩冬， 林京， 等． 自适应随机共振新方法及其在故障诊断中的应用[J]． 机械工程学报， 2012， 48(7)： 62-67．

[12] KENNDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks. Piscataway: IEEE Service Center, 1995: 1 942-1 948.

[13] ZHANG Y, GONG D W, DING Z H. Handling multi-objective optimization problems with a multi-swarm cooperative particle swarm optimizer[J]. Expert Systems with Applications, 2011, 38(11): 13 933-13 941.

[14] 李爱国. 多粒子群协同优化算法[J]. 复旦学报(自然科学版), 2004, 43(5): 923-925.

[15] 许珂, 刘栋. 多粒子群协同进化算法[J]. 计算机工程与应用, 2009, 45(3): 51-54.

[16] ZHANG J Z, DING X M. A multi-swarm self-adaptive and cooperative particle swarm optimization[J]. Engineering Applications of Artificial Intelligence, 2011, 24(6): 958-967.

[17] 吴思瑶, 姜绍飞. 基于DWT-FastICA和IMPSCO的时变结构损伤识别研究[J]. 福州大学学报(自然科学版), 2013, 41(4): 640-651.

[18] 翁柳青. 考虑传感器性能退化的结构损伤检测[D]. 福州： 福州大学, 2013.

(责任编辑： 洪江星)

Structuralmodalparametersidentificationbasedonadaptivestochasticresonancedenoising

YU Bo1, 2, LIU Zhanpeng1, JIANG Shaofei1

(1. College of Civil Engineering, Fuzhou University, Fuzhou, Fujian 350116, China; 2. Urban and Rural Construction Committee of Fuzhou City, Fuzhou, Fujian 350005, China)

Based on the challenge of structural modal parameters identification in the case of strong noise and low signal-to-noise ratio (SNR) environment and the deficiency of single parameter optimization in traditional adaptive stochastic resonance, this paper presents a new adaptive stochastic resonance method based on improved multi-particle swarm collaborative optimization (IMPSCO), which can perform multi-parameter synchronous optimization． Combined with Hilbert transform, the adaptive stochastic resonance algorithm can identify modal parameters of a structure. This algorithm can obtain the optimal structure parameters more quickly and adaptively realize optimal matching among the nonlinear system， input signal and noise． Therefore the noise of multi-frequency noisy signal is weakened and signal-noise-ratio (SNR) of the output is improved． The results from numerical simulation and a laboratory test conducted show that the proposed algorithm is simple and efficient in searching optimal parameters, furthermore enables to identify the structural modal parameters in case of strong noise.

adaptive stochastic resonance; particle swarm algorithm; strong noise; modal parameter identification

TU311.3

A

10.7631/issn.1000-2243.2017.04.0472

1000-2243(2017)04-0472-09

2017-02-24

姜绍飞(1969- )， 教授， 主要从事结构健康监测与组合结构方面的研究， cejsf@fzu.edu.cn

国家十二五科技支撑计划资助项目(2015BAK14B02)