塔式起重机运动惯性力引起货物摆动特性分析

董明晓，张恩，韩松君，王胜春

（山东建筑大学机电工程学院，山东济南250101）

塔式起重机运动惯性力引起货物摆动特性分析

董明晓，张恩，韩松君，王胜春

（山东建筑大学机电工程学院，山东济南250101）

塔式起重机机构运动容易引起货物摆动，降低了起重机的工作效率和安全性。通过分析机构运动惯性力引起的货物摆动特性，可为有效消除塔式起重机货物摆动提供控制理论和方法。文章根据Lagrange-Euler运动方程，建立塔式起重机动力学模型，推导了惯性力引起的货物摆动角度、角速度及货物摆动中心线倾斜角度的计算公式，通过实验仿真分析其摆动特性，并对机构运动惯性力引起的货物摆动最大角度进行估算。结果表明：塔式起重机变幅机构和回转机构运动惯性力使货物产生空间摆动；货物运动惯性力、离心力和科氏力的共同作用使摆动中心线发生倾斜，偏离了原来的平衡位置；货物运动的离心力和科氏力进一步加大了空间摆动的幅值。

塔式起重机；货物；惯性力；摆动幅值

Abstract：Cargo oscillation，induced bymechanism motions of tower cranes，reduceswork efficiency and safety of cranes.Therefore，it is necessary to analyze the swing performances induced by motion inertial forces of themechanisms to explore the control theories and methods for restraining the cargo oscillation.In this paper，the dynamicalmodels of the tower crane based on Lagrange-Euler equation ofmotion are set up and the oscillation characteristics induced by inertia force of the mechanism movements are analyzed.Then the calculation formula of the swing angle and angular velocity caused by the inertia force are deduced.The expression for calculating the inclination angle of the cargo oscillation centerline is proposed and the formula of the maximum oscillation angle induced by the inertial forces are put forward.The validity of the formula is proven by simulation.The simulation results show that themotion inertia forces of the translationmechanism and the rotation mechanism of the tower cranemake the cargo oscillate in space swing.The centrifugal force and the Coriolis force further increase the oscillation amplitude.The oscillation center line tilts are induced by the common effect of the inertia force，the centrifugal force and the Coriolis force and deviates from the original balance position.

Key words：tower crane；cargo；inertia force；oscillation amplitude

0 引言

起重机具有变幅、回转和起升运动3种基本工作状态，每个机构的运动都经历加速、匀速和减速运动，为了提高工作效率，通常变幅、回转和起升运动同时进行，这使货物的运动情况更加复杂——随着悬挂点移动，货物做变摆长的空间摆运动，其动力学特性表现为时变的非线性二阶振动特性。为了实现货物的准确定位和摆动控制，通常是将模型进行线性化处理，简化成平面单摆运动，然后提出消除货物摆动控制策略［1-3］。这一简化方法会降低消摆控制策略的实施精度，无法达到预期的控制效果［4-6］。而且没有对机构运动惯性力引起货物摆动的最大摆动角度进行估算，实现货物摆动预测控制的目的［7-9］。更没有研究货物惯性力引起的物摆动中心线倾斜角度，实现在货物运输过程中通过控制机构运动惯性力控制货物运动离心力和科氏力达到抑制货物摆动的目的［10-13］。为了解决上述问题，文章分析了变幅机构、回转机构和起升机构运动惯性力对货物摆动的影响规律，研究机构运动对货物空间摆动中心线的影响规律，并针对塔式起重机在无风的天气里运输大密度的货物，不计空气阻力和风载荷的情况下，推导出机构运动惯性力引起货物摆动的最大摆角计算公式，探索有效消除塔式起重机货物摆动提供控制理论和方法。

1 塔式起重机线性化模型

回转塔式起重机是通过变幅机构、回转机构和起升机构的运动达到运输货物的目的，根据货物的运动特性，建立极坐标系，其坐标原点取在起重机回转中心线与起重机回转平面的交点处。货物在小车运动的同时做空间摆动，并且随着起升机构的运动，摆长不断变化。根据这一运动特性建立非惯性直角坐标系和非惯性球坐标系，，坐标系的坐标原点取在小车上钢丝绳的悬挂点处，随着回转机构同步回转，并且随着变幅机构一起运动，建立的坐标系如图1所示［14］。

货物悬挂在小车上，在图1中将小车简化为一个质点，小车在坐标系中的位置是ρ和分别为小车的位移和回转角度，货物在坐标系中的位置用表示，l为起升机构钢丝绳长度，φ为起升机构钢丝绳与平面的夹角，θ为起升机构钢丝绳在平面上投影与过小车质点铅垂线的夹角。变幅机构运动的速度和加速度分别为回转机构运动的角速度和角加速度分别为，起升运动的速度和加速度分别为和，货物摆动角度为θ和φ。

图1 回转塔式起重机坐标系统图

根据Lagrange-Euler运动方程，在3大运行机构同时运动的情况下，建立塔式起重机非线性动力学模型［14］。由于 GB／T 3811—2008《起重机设计规范》规定，塔式起重机在运输货物时货物的摆动角度不得大于10°［15］，所以确定货物摆动的平衡位置θe＝0°和φe＝0°，在平衡位置附近将非线性化动力学模型作线性化处理，忽略高阶无穷小，得出塔式起重机在3大机构同时运动的情况下线性化动力学模型，由式（1）～（5）表示为

式中：Jm为回转机构的转动惯量，kg·m2；M为小车质量，kg；m为货物质量，kg；bρ为变幅机构运动阻尼系数，N·s／m；bψ为回转机构运动阻尼系数，N·s／m；bl为起升机构运动阻尼系数，N·s／m；Fρ为变幅机构驱动力，N；Fψ为回转机构驱动力，N；Fl为起升机构驱动力，N；g为重力加速度，m／s2。

式（1）～（5）是塔式起重机变幅运动、回转运动、起升运动和货物摆动的线性化动力学模型，以式（4）为例说明惯性力、离心力和科氏力的大小。将式（4）乘以货物质量m，就变为货物摆动的动力学方程，由式（6）表示为

2 惯性力引起的货物摆动特性分析

2.1 惯性力引起货物摆动的角度和角速度分析

2.1.1 计算公式

根据式（1）～（5）可知，货物摆动角度θ（t）和φ（t）主要是由变幅机构和回转机构运动惯性力引起的，如果变幅机构和回转机构同时运动，将使货物产生空间摆运动，并且回转机构运动的离心力和科氏力加大了空间摆的摆动幅度，使摆动中心线发生倾斜。如果3大机构以最大的加速度进行起、制动，将引起货物最大的摆动。从式（1）～（5）推导出变幅机构运动惯性力和回转机构运动惯性力引起的货物摆动计算公式，由式（7）、（8）表示为

式（7）的通解由式（9）表示为

式中：c1、c2分别为由起重机系统初始状态决定的待定系数；ωn为货物摆动的固有频率l。起重机系统通常情况下初始状态为0，所以货物摆动角度和角速度可以由式（10）、（11）表示为

将式（10）、（11）用泰勒级数展开，且忽略高次项，式（10）、（11）化简成式（12）、（13）表示为

2.1.2 实验仿真分析

按照z-135塔式起重机以1∶30的比例设计回转塔式起重机模拟实验台［14］，试验台参数如下：小车质量M为1.5 kg，货物质量m为1 kg，变幅机构最大运动加速度 amax为 1 m／s2，额定速度 vmax为0.5 m／s，阻尼系数为 0.1 N·s／m，变幅机构加速运动 0.5 s，匀速运动 9 s，再减速运动 0.5 s；回转机构转动惯量 Jm为 5.5 kg·m2，额定回转速度为0.1 rad／s，回转机构加速回转 0.5 s，然后匀速回转9 s，再减速回转0.5 s；起升机构额定运动速度为0.2 m／s，起升机构钢丝绳长度由 0.8 m 提升到0.4 m，再下降到0.8 m。

货物摆动角度θ（t）和φ（t）如图2所示。从图2可以看出变幅机构运动惯性力引起的货物摆动角度θ（t）变化不大，货物摆动角度幅值φ（t）随着变幅机构的运动和回转幅度的增大而不断增大。

图2 货物摆动角度图

2.2 货物摆动中心线的倾斜角度分析

2.2.1 计算公式

随着变幅机构和回转机构的运动，货物开始做空间摆运动，其摆动的中心线开始倾斜。起升运动不影响货物摆动中心线的位置，但影响货物自由摆动延续时间的长短。而变幅机构运动加速度和回转机构运动速度使货物摆动的中心线发生倾斜，摆动中心线的倾斜角度 θe和 φe分别由式（14）、（15）［14］表示为

式（14）、（15）描述了变幅机构运动和回转机构运动对货物摆动中心线的作用规律。变幅机构和回转机构的运动位移、速度和加速度使货物摆动中心线发生倾斜，相当于货物在倾斜的重力场内做空间摆运动，摆动中心线也是货物空间摆的平衡位置。

2.2.2 实验仿真分析

对货物摆动中心线的倾斜角度进行仿真计算，仿真计算参数同图2的仿真参数。货物摆动角度中心线 θe（t）和 φe（t）如图3所示。

图3 回转塔式起重机货物摆动中心线图

由图3可以看出，货物摆动中心线与变幅加速度成近似线性关系，当小车加速运行时，货物摆动中心线向反方向摆动；当小车匀速运行时，货物摆动中心线不发生倾斜。货物摆动中心线 φe（t）与 θe（t）有着相似的关系，只是由于回转运动离心力的存在使货物摆动中心线φe（t）不为零，随着回转半径的增加，离心力逐渐加大，φe（t）越来越大，回转运动离心力对货物摆动中心线φe（t）影响较大。当变幅机构和回转机构运动的位移、速度和加速度超过一定值时，不再满足非线性化处理条件，应求解新的平衡位置，在新的平衡位置附近进行模型线性化处理。

2.3 惯性力引起货物摆动的最大摆动角度分析

塔式起重机以最短时间起动，在完成起动瞬间货物摆动角度 θ（t）和角速度满足即变幅运动引起最大摆速同理，回转运动引起货物最大摆速

对于密度大、体积小的货物，空气阻力的影响非常小［16］，且GB／T 3811—2008规定，在风力大于6级的天气里不允许操作起重机［15］。因此，只针对塔式起重机在无风的天气里运输大密度的货物的情况，不计空气阻力和风载荷，推导惯性力引起货物摆动的最大摆动角度的估算公式。根据能量守恒定律，估计惯性力引起货物摆动的最大摆角度公式，由式（16）、（17）表示为

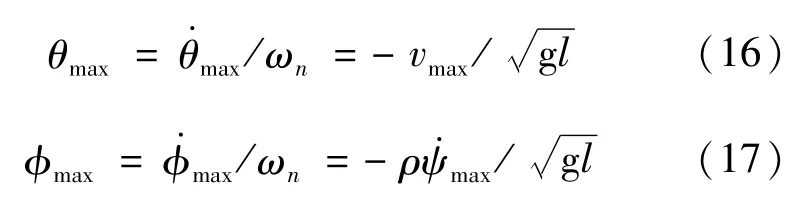
式（16）、（17）揭示了起重机变幅机构和回转机构的动力学参数对货物摆动的最大幅值的作用规律。根据式（16）、（17）的推导可以得出：当起升高度和变幅机构运动速度满足l＜（18vmax）2／（π2g）时，货物的摆动角度 θ（t）大于 10°。根据 GB／T 3811—2008规定，货物的摆动角度不得大于10°，因此这将超过起重机操作规程中货物摆动角度的规定，属于危险作业，应该停止操作；当起升高度和回转机构回转速度满足时，货物摆动角度φ（t）大于10°，也超过起重机操作规程中货物摆动角度的规定。在这种情况下，应该根据式（14）、（15）重新计算货物摆动的平衡位置，重新推导式（1）～（5），作为起重机系统线性化模型。

3 结论

通过上述研究表明：

（1）塔式起重机变幅机构和回转机构运动惯性力引起货物摆动，在小车的匀速运动过程中，在变幅机构运动平面内的货物摆动角度和角速度变化不大；随着回转幅度的增大，在回转运动切向平面内的摆动角度和角速度逐渐增大。

（2）离心力和科氏力的共同作用使摆动中心线发生倾斜，偏离了原来的平衡位置，线性化模型存在这较大误差，应重新计算货物摆动的平衡位置，建立新的起重机线性化模型。

（3）随着变幅运动和回转运动的进行，货物运动的离心力和科氏力逐渐增大，货物将产生更大幅度的空间摆动，将超出起重机安全操作规程中规定的最大摆动角度，导致起重机操作不安全。

［1］ Kim D.，Park Y..Tracking control in x-y plane of an offshore container crane［J］.Journal of Vibration and Control，2015，7（1）：1-15.

［2］ Fang Y.C.，Zhang Y.C..Dynamics analysis and nonlinear control of an offshore boom crane［J］.IEEE Transactions on Industrial Electronics，2014，16（1）：414-427.

［3］ Kiviluoto S.，Eriksson L.，Koivo H.N..Modelling and control of vertical oscillation in overhead cranes［C］.Chicago：2015 American Control Conference，2015.

［4］ Fujioka D.，Shah M.，Singhose W..Robustness analysis of input-shaped model reference control on a double-pendulum crane［C］.Chicago：2015 American Control Conference，2015.

［5］ Yoon J.，Vaughan J.E..Control of crane payloads that bounce during hoisting［J］.IEEE Transactions on Control Systems Technology，2014，22（3）：1233-1238.

［6］ Kumada T.，Chen G.，Takami I..Adaptive control for jib crane with nonlinear uncertainties［C］. Kathmandu：12th IEEE International Conference on Control＆ Automation（ICCA），2016.

［7］ Zhang X.B.，Sun N..Minimum-time trajectory planning for underactuated overhead crane systems with state and control constraints［J］.IEEE Transactionson Industrial Electronics，2014，61（12）：6915-6925.

［8］ Lu B.，Fang Y.C.，Sun N..Modeling and verification for a four-rope crane［C］. Shenyang： The 5th Annual IEEE International Conference on Cyber Technology in Automation，Control and Intelligent Systems，2015.

［9］ Smoczek J.，Szpytko J..Particle swarm optimization-based multivariable generalized predictive control for an overhead crane［J］.IEEE-ASME Transactions on Mechatronics，2017，22（1）：258-268.

［10］ Donaire A.M.R.，Singh N.M..Shaping the energy of mechanical systems without solving partial differential equations［J］.IEEE Transactions on Automatic Control，2016，64（4）：1051-1056.

［11］Sun N.F.Y.，Fu Y.M..Slew／translation positioning and swing suppression for4-DOF Tower craneswith parametric uncertainties：design and hardware experimentation［J］.IEEE Transactions on Industrial Electronics，2016，63（10）：6407-6418.

［12］Kurabayashi T.，Yang C.，Murakami T..An advanced position control of overhead crane by sway suppression method emulating natural damping［C］.Hiroshima：The 2014 International Power Electronics Conference，2014.

［13］Farag S.A.，Foda S.G.，Alenany A..Fuzzy control of a large crane structure［J］.European Journal of Engineering Research and Science，2016，1（6）：68-73.

［14］董明晓.实现起重机自动化的时滞控制理论及应用研究［D］.西安：西安交通大学，2005.

［15］GB／T 3811—2008，起重机设计规范［S］.北京：中国标准出版社，2008.

［16］董明晓，郑康平，张明勤，等.回转起重机载荷摆动建模误差及不确定性定量分析［J］.应用基础与工程科学学报，2005，13（1）：75-80.

（学科责编：赵成龙）

Analysis of cargo oscillation caused by inertia force ofmechanism motions for tower cranes

Dong Mingxiao，Zhang En，Han Songjun，et al.
（School of Mechanical and Electrical Engineering，Shandong Jianzhu University，Jinan 250101，China）

TH213

A

1673-7644（2017）04-0307-04

2017-06-26

国家自然科学基金项目（51475277）；山东省高端外国专家项目（370020121030）；山东省科技发展计划项目（2013GCG20303）

董明晓（1965-），女，教授，博士，主要从事机电系统运动控制、振动控制等方面的研究.E-mail：mxdong＠sdjzu.edu.cn