分类讨论思想在高考导数问题中的应用

河北易县中学 边红霞

分类讨论思想在高考导数问题中的应用

河北易县中学 边红霞

分类讨论是高中数学中一种重要的思想方法，同时也是一种重要的解题策略，体现了化整为零的思想，它在解答数学问题时发挥着重要的作用，并贯穿于中学数学始终。它揭示了研究对象之间的内在规律，有助于数学思维的培养和锻炼，能够使分析问题达到由繁到简的目的，有利于锻炼学生思维的逻辑性、综合性、探索性，使问题思考条理化、有序化。

一、分类讨论的依据

分类讨论是根据研究的数学对象在不同情况下得到不同的结论而进行的。大致可以分为：①每个数学结论都有其成立的条件；②每一种数学方法的使用都有其适用范围；③有些图形的位置不是唯一的；④有些问题在解题时不能以统一的形式进行研究；⑤已知量是用字母表示的，字母的取值影响问题的解决等。

二、分类讨论的标准

一般地，在集合C上讨论某一数学问题时，可根据某个标准P，把C划分为C1,C2,C3,……Cn,这时，在C1,C2,C3,……Cn上分别实施讨论，等价于在A上实施对问题的讨论，把P就叫作分类讨论的标准。

三、分类讨论的原则

为了解决数学问题，分类旨在化大为小，分散难点，操作程序是各个击破。分类时，要遵循以下原则：①②保证研究的问题不会重复；③保证研究的问题不会有遗漏。近几年高考解答题中的导数问题在求解时大都是结论不唯一，都需要分类讨论，本文将详细叙述导数问题中分类讨论思想的使用。

例1 （2016年全国新课标卷Ⅰ 理科数学第21题）已知函数有两个零点。

（Ⅰ）求a的取值范围；

解：函数的零点是指函数图象与x轴交点的横坐标，确定方法是只要在区间上满足则在上必存在x0，使得

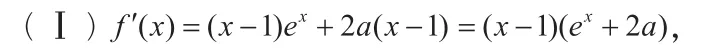
此时，在这道题目中要想确定其零点，题目中含有字母a，它的符号影响了导数对应方程的跟根，因此需对a的符号展开讨论：

分析：本题主要是考查导数的应用，在求解过程中考查数形结合思想、分类讨论思想、函数思想，考查运算求解能力及逻辑思维能力。此题充分利用数形结合，同时使用了构造函数求极值、证明不等式，这是这道题目的最大亮点。

例2 （2015年全国新课标卷Ⅰ 理科数学第21题）已知函数

图1

图2

评析：此题考查了导数的几何意义，利用导数比较函数值的大小，考查了分类讨论思想及数形结合思想，考查综合分析问题及解决问题的能力。

以上近几年的高考导数问题充分考查了分类讨论思想，并在解题的过程中又淋漓尽致地使用了数形结合，同时还用到了化归思想和转化思想，因此，数学思想方法是解决数学问题最本真的方法，特别是在高考导数题目中发挥着巨大作用。往往是在解决问题的全过程中，不断地把复杂问题简单化，化整为零，各个击破，同时，通过数与形的结合，将抽象的问题具体化，这样使解题过程实现一路绿灯，顺畅通行。