运用生活经验解决数学动态问题
江苏联合职业技术学院常州铁道分院 张 颖
运用生活经验解决数学动态问题
江苏联合职业技术学院常州铁道分院 张 颖
现在越来越多的中考数学题偏向于用动态的表现形式来提高考题的难度,考查学生的观察能力、缜密的思维想象能力、与实际生活结合的数学知识运用能力。本文通过对常见题型的简单分类,结合具体例题的分析,阐述解决此类问题的基本途径。
生活经验;数学动态
动态问题一直是历年来的中考热点,目的是考查学生运用数学思想探究、解决问题的能力,其难度在于涉及知识面广,综合性强。
通常所见的几类动态问题包括:(1)动点问题,指动点沿着确定的某种未知路径运动,解答方法一般是利用特殊图形建立方程。(2)动线或动图问题,指直线或图形按某种要求进行平移、旋转、翻折形成新图形,此种情况要求利用全等三角形或相似三角形建立方程或函数关系解答。要成功解决动态问题,关键要把握两点:(1)明确运动过程。首先,以动制静,结合题目条件和图形想象运动的全过程,初步确定运动过程中的几种状态;其次,以静制动,结合运动的状态,确定有代表性的图形。(2)找准解题手段。运用分类讨论、转化的数学思想,结合图形,选择方程、函数或不等式来寻找等量关系,进行计算。
有些动态问题不仅考验学生日常生活中的细微观察能力,同时也要求学生有缜密的思维来建立数学方程的模型,两者缺一不可。
例如:实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1∶2∶1,用两个相同的管子在5cm高度处连通(即管子底离底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示。若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升
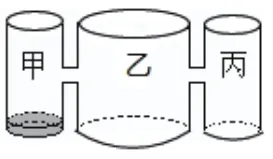
解析:(1)∵甲、乙、丙三个圆柱形容器(容器足够高)底面半径之比为1∶2∶1,∴若每分钟向容器注入相同量的水,水面上升高度之比为半径平方的反比。
(2)假设开始注入t分钟的水量后,甲与乙的水位高度之差是0.5cm,分三种情况:
①当乙的水位低于甲的水位,甲的水位不变时,
②当乙的水位高于甲的水位,甲的水位不变时(乙中水未流向甲),
③当乙的水位高于甲的水位,乙中的水往甲中溢出(到达管子底部),甲的水位上升时,
∵乙中的水到达管子底部,即水位高度达到5cm的时间包含两部分(丙中水未向乙溢出之前和丙中水向乙溢出之后):
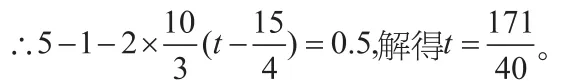
这道题实质是一元一次方程的应用,知识点本身难度不高,但背后却隐藏了一些生活中的物理小常识,而且学生还必须在短时间里对出现的所有情况做出细致全面的判断,特别是三个容器水位的高度直接影响着水的流向,这就不容易做到了。要提高学生解决动态问题的效率,除了熟练掌握涉及的基本知识,平时还要加强运用分类讨论、数形结合、转化的思想来分析考虑问题;灵活掌握点坐标、运动路程与线段长的相互转化等一系列有效的计算方法和技巧;同时,对学生想象能力的培养也不容忽视。
【备注:本文系基金项目:江苏省职教学会2017-2018年度职业教育研究课题《五年制高职校文化课教研室建设现状与策略研究——以常州铁道高等职业技术学校为例》(XHXS2017107)。】
张颖(1977-),女,江苏常州人,数学教研室主任,副教授,硕士,中国数学奥林匹克一级教练员,主要从事数学教学和教育管理研究。)

