不确定区间二型离散系统的广义H2控制器设计

王雪飞,周绍生

(杭州电子科技大学自动化学院,浙江 杭州 310018)

不确定区间二型离散系统的广义H2控制器设计

王雪飞,周绍生

(杭州电子科技大学自动化学院,浙江 杭州 310018)

研究了一类不确定区间二型离散系统的广义H2控制问题，根据Lyapunov稳定性理论和矩阵不等式放缩技巧，建立了使闭环系统渐近稳定且具有广义H2范数界的充分条件.利用二型模糊基函数的特性引入松弛矩阵，并使用矩阵分解技巧对具有不确定性的参数矩阵进行了处理.最后，通过仿真实例验证了设计方法的可行性.

区间二型T-S模糊系统；离散系统；广义H2性能；不确定；前提不匹配

0 引 言

为了掌控系统更多的不确定性信息，Lotfi Z.[1]在一型模糊集合的基础上引入了二型模糊集合.之后，Jerry M.M.等[2]又提出了区间二型模糊集合的概念.区间二型模糊集的隶属函数是三维的，其中次隶属函数定为1，因而既表征了一型模糊集合隶属函数上的不确定性，又降低了一般二型模糊集合运算推理的复杂度，是解决二型模糊系统稳定性分析和镇定问题的有力工具.文献[3]考虑了离散区间二型模糊系统不确定域中包含的不确定信息，引入了松弛矩阵，得到了保守性更小的稳定性约束条件.另一方面，由于非线性扰动在实际控制系统中不可避免，在不确定允许扰动范围内的H2或H∞保性能控制问题也引起了许多研究者的关注[4-5].文献[5]研究了一类一型离散T-S模糊系统的广义H2控制问题.本文主要研究了不确定区间二型离散T-S模糊系统的广义H2控制问题，设计的状态反馈控制器使得闭环系统渐近稳定并具有广义H2范数界.利用矩阵不等式缩放技巧、矩阵分解技巧及Schur补引理，建立了线性矩阵不等式，并根据二型模糊基函数的特性引入松弛矩阵，从而给出保证闭环系统渐近稳定且保守性更小的充分条件.

1 系统描述

基于T-S模型的不确定区间二型离散模糊系统的第i个IF-THEN规则如下式所描述：

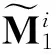
(1)

(2)

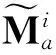
(3)

Δ=[I-F(k)J]-1F(k)

(4)

F(k)F(k)T≤I

(5)

I-JJT>0

(6)

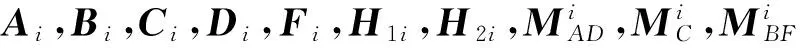
由上述可得不确定区间二型离散T-S模糊系统的最终描述为：

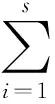
(7)

(8)

设计前提不匹配的状态反馈控制器，其中第j个规则描述为：

u=Kjx(k),j=1,…,s

其中，Kj∈m×n是第j个控制规则的反馈增益.则状态反馈控制器最终描述为：

(9)

(10)

(11)

闭环系统的广义H2范数定义为：

对于给定的γ>0，若存在控制器使得当ω(k)≡0，闭环系统的广义H2范数小于γ时，则闭环系统被认为是具有广义H2范数界的.

引理[6]如果Δ满足式(3)—(6)且有M=MT，S，N为适合维数矩阵，若对于所有F(k)满足式(4)，则不等式

M+SΔN+NTΔTST<0

(12)

成立，当且仅当存在ε>0，有如下矩阵不等式成立：

(13)

2 主要成果

定理满足式(3)—(6)线性分式形式的区间二型离散闭环模糊系统Σ在控制器增益Kj=MjX-1作用下渐近稳定且具有广义H2范数界的充分条件是：存在正定矩阵X=XT∈n×n,Mj∈m×n及适合维数矩阵在ηj-δjhj≥0(0<δj<1)条件下使得下列线性矩阵不等式成立.

(14)

(15)

(16)

(17)

其中，

证明选择Lyapunov方程

V(k)=x(k)TPx(k)

(18)

其中，P=PT∈n×n>0.定义由式(10)和(18)可得：

对任意N∈{1,2,…}，令

对任意非零扰动ω(k)∈l2[0,∞)和零初始条件x(0)=0，有

(19)

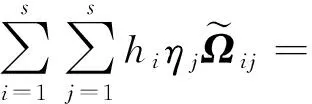
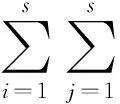
(20)

由式(14)—(16)、式(20)可得

(21)

(22)

根据式(22)结合引理，有：

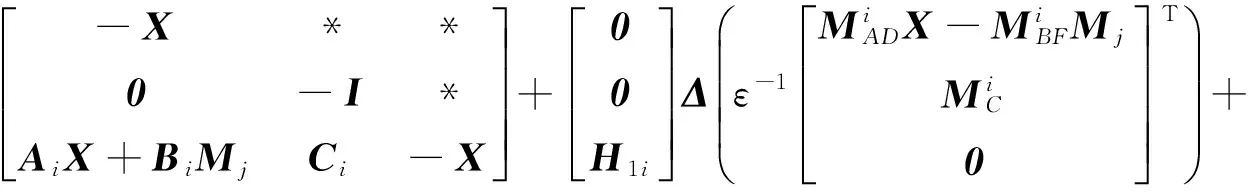
(23)

计算式(23)并结合式(3)，可得：

(24)

定义P=X-1，Kj=MjX-1，并对式(24)进行Schur补变换，可得

(25)

用对角阵diagX-1,I分别左乘和右乘不等式(25)得到

(26)

比较式(19)和式(26)，可得JN<0，即

(27)

接下来验证对于给定的γ>0，系统是否具有广义H2范数界.由

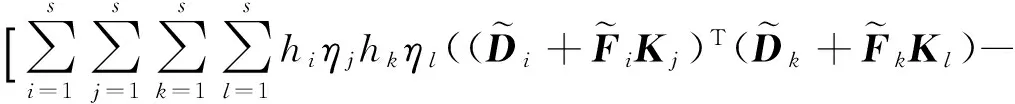
(28)

同理，对式(17)进行矩阵分解后用diag{X-1,I,I}分别左乘和右乘，再使用Schur补引理，得到：

(29)

比较式(28)与式(29)，可以验证，对于任意N及ω(k)∈l2[0,∞)，有

z(N)Tz(N)-γ2V(N)<0

(30)

由式(27)和式(30)可以得出不确定区间二型离散闭环系统Σ是渐近稳定且具有广义H2范数界的.证毕.

3 数值仿真

对于离散模糊系统Σ，参考文献[4-5]方法，当s=2且各参数矩阵选取如下：

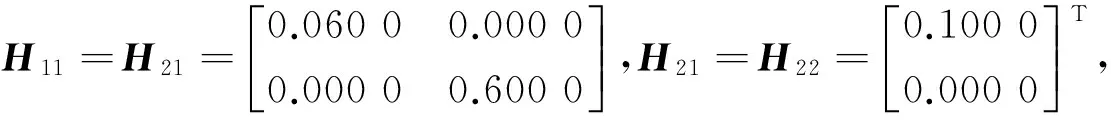
开环系统和闭环系统下状态响应和控制输出响应的仿真结果分别如图(1)—(4)所示.部分初始参数为：x1(0)=0.5，x2(0)=-1.5，仿真时长T=60，ω(k)=1/(1+k2).

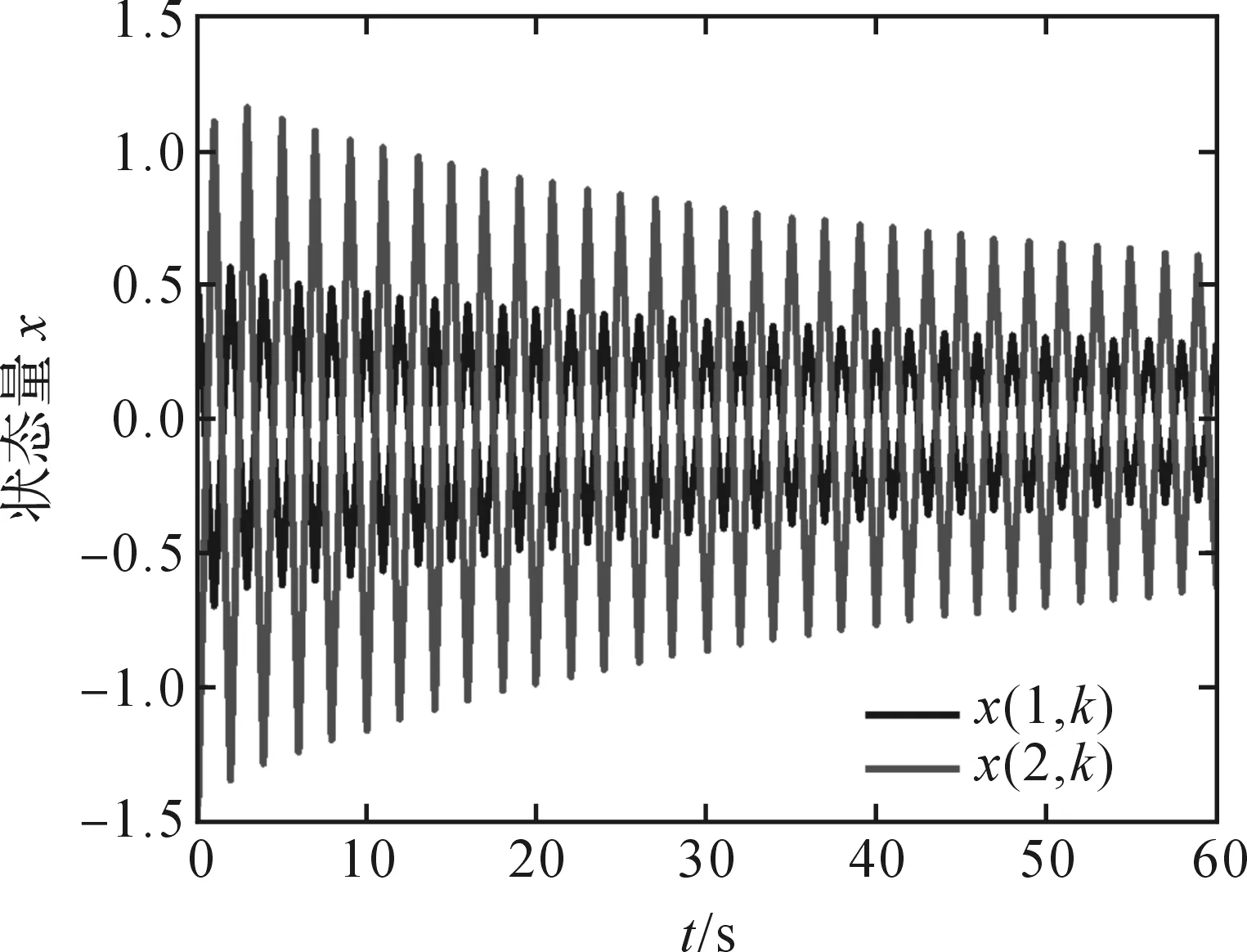
图1 开环系统状态响应

图2 开环系统控制输出响应

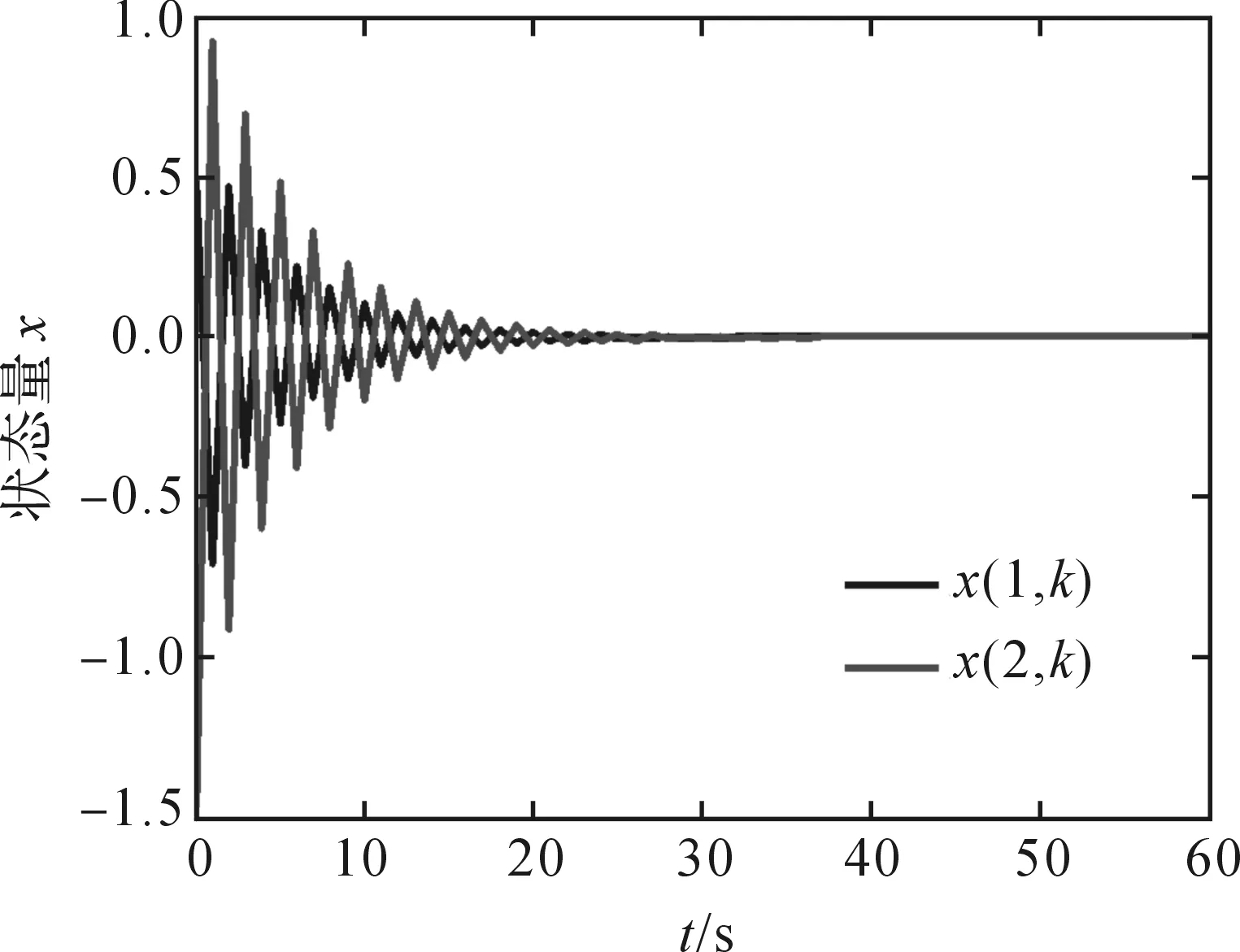
图3 闭环系统状态响应

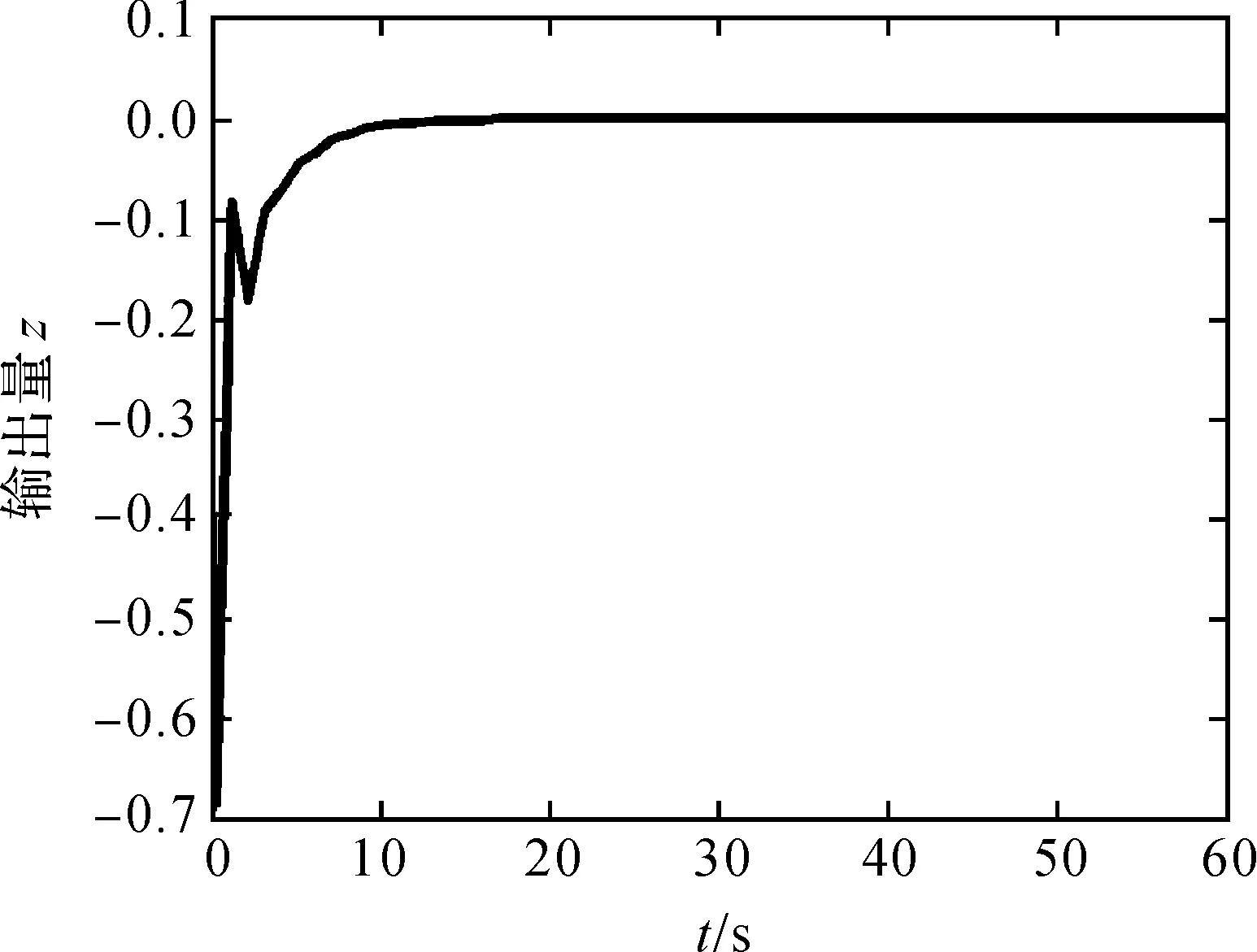
图4 闭环系统控制输出响应

由图(1)—(4)可知，开环系统下，状态响应和控制输出响应随着时间的延续是不断发散的，在本文设计的控制器作用下，响应曲线在一定时间后均趋于零点，因此闭环系统Σ是全局渐近稳定的.

4 结束语

本文主要研究了一类不确定区间二型离散系统的广义H2控制问题.采用不等式放缩、矩阵分解等技巧，结合二型模糊基函数的特性给出了系统稳定性约束条件的LMI形式，解决了具有线性分式结构参数不确定性的二型系统的控制器设计难题，从而为区间二型模糊系统的保性能控制问题的研究打下了一定的基础.

[1] ZADEH L A. The concept of a linguistic variable and its application to approximate Reasoning-I[J]. Information Sciences, 1975,8(3):199-249.

[2] MENDEL J M, JOHN R I B. Type-2 fuzzy sets made simple[J]. Fuzzy Systems, IEEE Transactions on, 2002,10(2):117-127.

[3] SHENG L, MA X Y. Stability analysis and controller design of discrete interval type-2 fuzzy systems[J]. Asian Journal of Control, 2014,16(4):1091-1104.

[4] ZHOU S S, FENG G. GeneralisedH2controller synthesis for uncertain discrete-time fuzzy systems via basis-dependent Lyapunov functions[J]. IEE Proceedings - Control Theory and Applications, 2006,153(1):74-80.

[5] ZHOU S S, FENG G, LAM J, et al. Robust H-infinity control for discrete-time fuzzy systems via basis-dependent Lyapunov functions[J]. Information Sciences, 2005,174(3):197-217.

GeneralizedH2ControllerSynthesisforIntervalType-2UncertainDiscrete-timeFuzzySystems

WANG Xuefei, ZHOU Shaosheng

(SchoolofAutomation,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

The generalizedH2controller design problem is investigated for a class of interval type-2 discrete-time fuzzy systems with uncertainties. Using matrix inequality techniques and Lyapunov approach, a sufficiency condition for stability of the close-loop systems with generalizedH2-norm bound is developed. Relaxed matrixes are introduced with the properties of type-2 fuzzy basis functions, matrix decomposition techniques are adopt to deal with parameter uncertainties. Finally, the simulation results show the effectiveness of the proposed approach.

interval type-2 T-S systems; discrete-time systems; guaranteedH2performance; uncertain; imperfect premise matching

TP273

A

1001-9146(2017)05-0051-06

10.13954/j.cnki.hdu.2017.05.010

2016-11-14

国家自然科学基金资助项目(61673149)；国家自然科学基金资助项目(61273093)

王雪飞(1992-),男,安徽六安人,硕士研究生,先进控制理论.通信作者:周绍生教授,E-mail: sszhou@hdu.edu.cn.