超浅埋地铁站通道爆破暗挖地表振动传播特征
张震,周传波,路世伟,吴超,王超
超浅埋地铁站通道爆破暗挖地表振动传播特征
张震,周传波,路世伟,吴超,王超
(中国地质大学(武汉) 工程学院,湖北武汉,430074)
结合武汉市轨道交通2号线工程背景,采用现场监测和动力有限元数值模拟相结合的研究方法,对超浅埋通道下台阶爆破开挖地表振动传播规律进行研究。同时,为研究上台阶开挖空间对爆破地震波传播特征的影响,对通道全断面爆破开挖的地表振动传播规律进行数值模拟分析。研究结果表明:下台阶爆破开挖工况下,沿通道开挖导洞轴线方向,由于应力波的绕射,掌子面前方5 m处地表质点峰值振速达到最大值;垂直于通道开挖导洞轴线方向,掏槽孔孔底连心线中点正上方地表质点与爆源距离最小,但峰值振速并不是最大,且质点两侧2 m范围内,随着爆心距的增加,峰值振速不断增大。全断面爆破开挖工况下,沿通道开挖导洞轴线方向,掌子面前方2 m处地表质点峰值振速达到最大值;垂直于通道开挖导洞轴线方向,掏槽孔孔底连心线中点正上方地表质点峰值振速最大,且随着爆心距的增加,峰值振速不断减小。对比通道下台阶爆破开挖和全断面爆破开挖2种工况下地表质点振动特征,上台阶开挖空间的存在阻隔了应力波的传播,在一定空间范围内影响爆破地震波的传播特征,能够有效降低地表质点峰值振速。
地下通道;爆破开挖;数值模拟;地表振动;传播规律
地下空间岩石开挖大多采用钻爆法。城市地下工程多在环境复杂、人口密集的城市中心地带,钻爆法施工产生的地震效应可能危及周边安全[1−3]。了解地下空间爆破开挖引起的地表振动特性和传播规律,是安全控制爆破开挖的前提[4−5]。目前,研究者对浅埋隧道爆破开挖地表振动传播规律研究较多[6−8]。高文学等[6]通过现场地表振动监测,研究了上台阶爆破开挖工况下沿隧道轴向地表振动传播规律;李利平等[7]系统分析了现场监测地表振速,对地表振动的爆破动力特性进行了研究;肖文涛等[8]用萨道夫斯基公式对现场监测地表振速进行拟合,并用动力有限元数值模拟的方法对上台阶爆破开挖工况下地表振动规律进行分析。总体来看,学者对上台阶人工开挖情况下超浅埋隧道下台阶爆破开挖地表振动规律研究少有涉及。本文作者结合武汉市轨道交通二号线宝通寺站Ⅳ号出口过街通道工程实际,以现场实测地表爆破振动数据为基础,采用动力有限元数值模拟方法,研究了超浅埋通道下台阶爆破开挖作用下沿通道轴向及垂直于通道轴向地表振动传播规律。为了研究上台阶开挖空间对地表爆破地震波传播特征的影响,对通道全断面爆破开挖的地表振动规律进行数值模拟分析并与下台阶爆破开挖工况下地表振动规律对比。
1 工程概况
宝通寺车站Ⅳ号出口过街通道为超浅埋,暗挖段埋深4.0 m,总长57.77 m,其中标准段长53.17 m,标准段净空高6.14 m,宽6.46 m。过街通道暗挖段采取CD法分为2个导洞开挖,每个导洞分上下台阶分步开挖。通道上台阶为粉质黏土层,厚度为2.0~2.5 m,采取人工挖除,与下台阶错开2.0~3.0 m的超短台阶。下台阶为粉砂质泥岩,厚度为3.5~4.0 m,采取爆破方式开挖,爆破开挖循环进尺为1.0 m。
在隧道爆破开挖时,掏槽孔爆破造成的地震效应通常最为强烈[9],根据爆破设计方案,右导洞掏槽孔装药量明显大于左导洞,按最不利安全条件考虑,对右导洞爆破开挖作用下地表振动规律进行研究。通道掏槽爆破示意图如图1所示。炮孔直径为40 mm,采用耦合装药,单孔装药量为0.3 kg,起爆方式为孔底同时起爆。
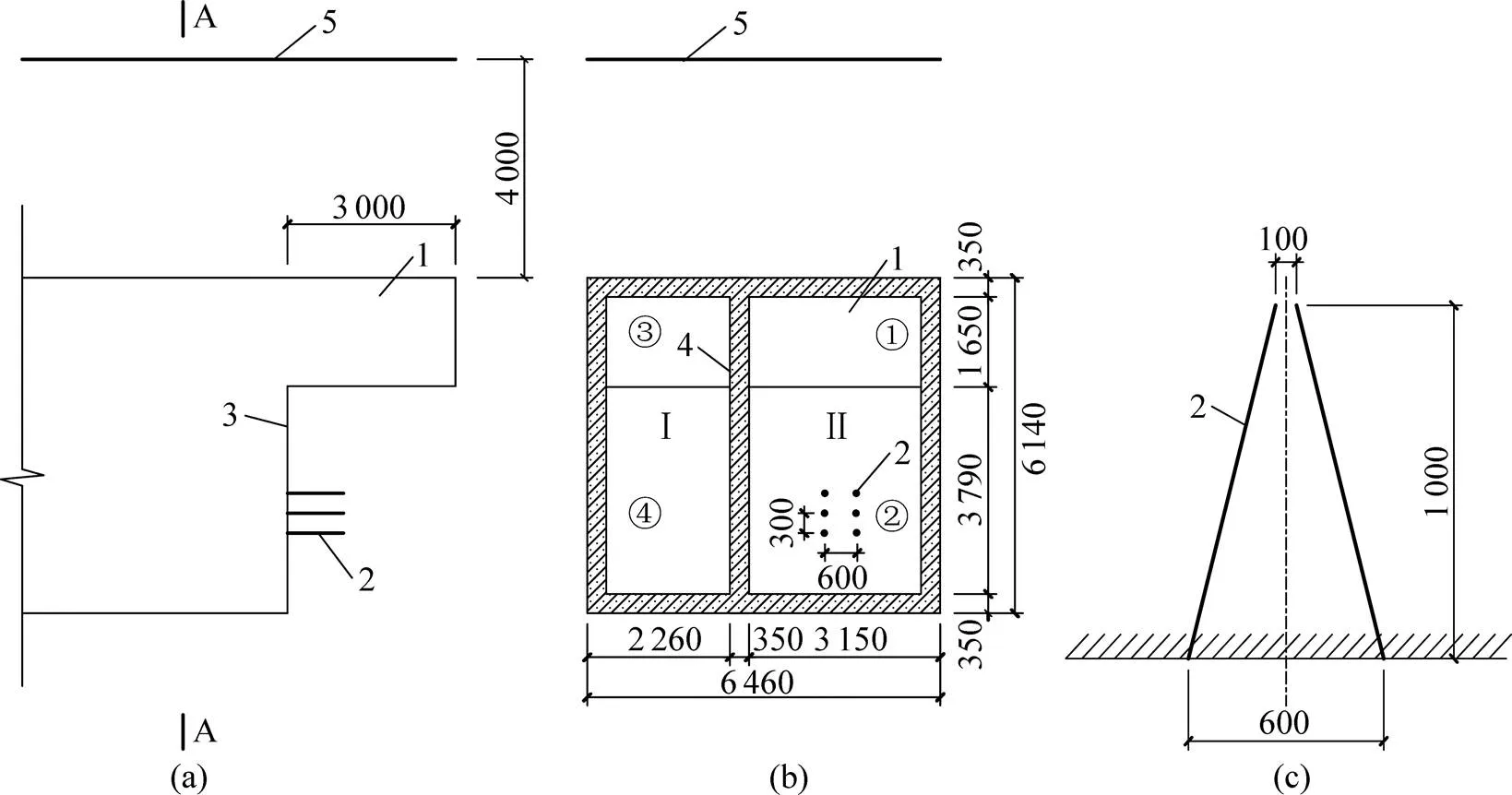
(a) 纵断面示意图;(b)-横断面示意图;(c) 掏槽孔布置平面示意图
1—人工挖空区(粉质黏土层);2—掏槽孔;3—掌子面;4—衬砌;5—地表;Ⅰ—左导洞;Ⅱ—右导洞
①,②,③,④—开挖顺序。
单位:mm
图1 通道掏槽爆破示意图
Fig. 1 Schematic diagram of underpass cut blasting
2 数值模型及其验证
2.1 模型尺寸及边界条件
采用动力有限元程序ANSYS/LS-DYNA对通道掘进的掏槽孔爆破进行模拟。图2所示为通道下台阶爆破开挖工况下掏槽爆破时的模型。模型整体尺寸(长×宽×高)为40 m×40 m×18 m,地表土层厚度为 6 m。模型中材料均采用Soild164单元划分为Lagrange网格。在关于有限元的动力学数值模拟中,KUHLEMEYER等[10]认为为了能够精确模拟应力波的传播,模型网格的单元尺寸须小于输入波波长的1/10~1/8,而网格太密太细会占用大量的分析时间,综合考虑,土体单元网格尺寸为0.5 m,对岩体单元网格尺寸进行适当粗划以减少单元数量。模型共划分448 019个单元,计算采用cm-g-μs单位制。模型中除顶面及通道轮廓为自由边界外,其余边界均采用无反射边界。
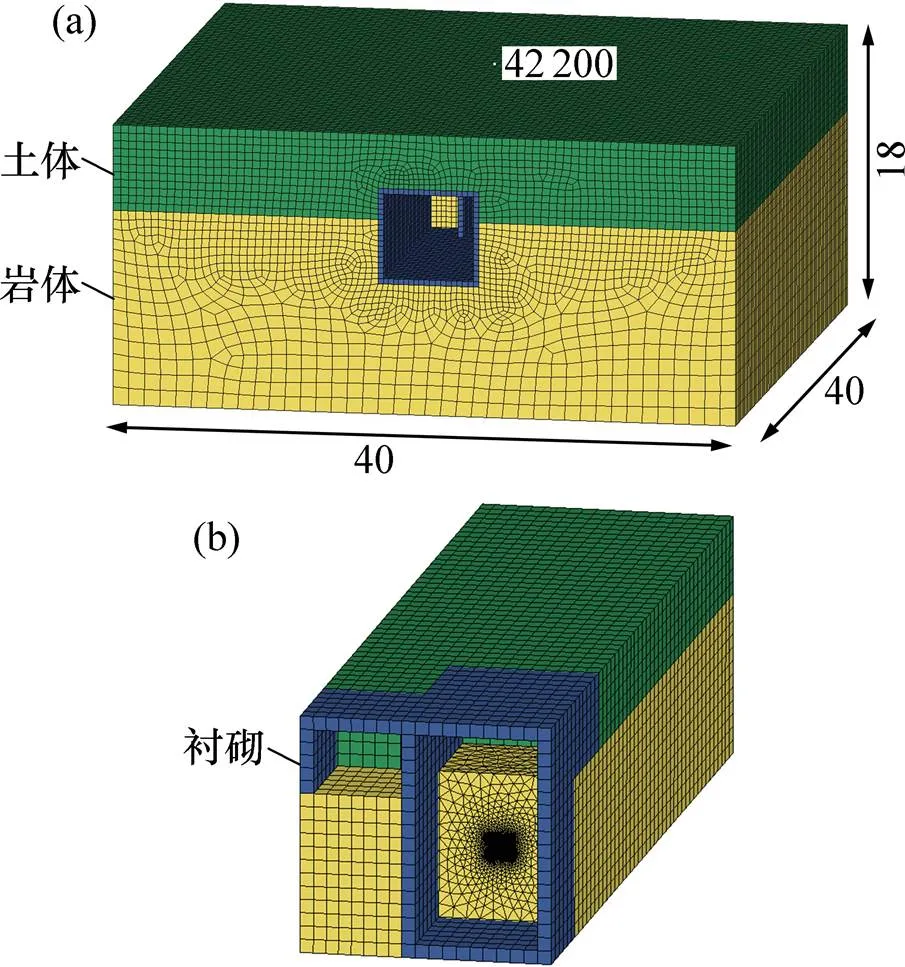
(a) 整体模型;(b) 开挖断面处网格划分
2.2 材料模型及参数
计算模型包括炸药、围岩、上覆土体及衬砌材料。炸药为2号岩石乳化炸药;围岩为粉砂质泥岩,选用MAT_PLASTIC_KINEMATIC材料模型[11−13],该材料模型考虑了岩石介质材料的弹塑性性质,并能够对材料的强化效应(随动强化和各向同性强化)和应变率变化效应加以描述;土体采用MAT_DRUCKER_PRAGER材料模型[14−16],该材料模型能有效模拟土体特性,且用于定义屈服面的岩土参数简单易得;衬砌采用MAT_ELASTIC弹性模型。岩土体及衬砌物理力学参数见表1~3。

表1 围岩物理力学参数

表2 土体物理力学参数

表3 衬砌物理力学参数
模拟炸药爆轰过程中压力和比容的关系为JWL状态方程[17]:
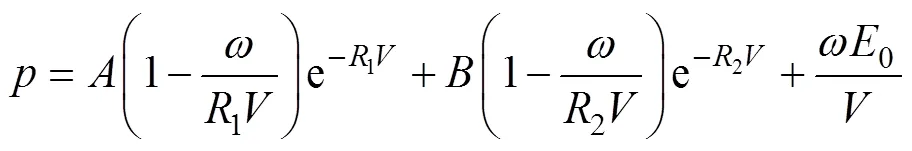
式中:,,1,2和为材料常数;为压力;为相对体积;0为初始比内能。炸药材料的主要输入参数见表4。
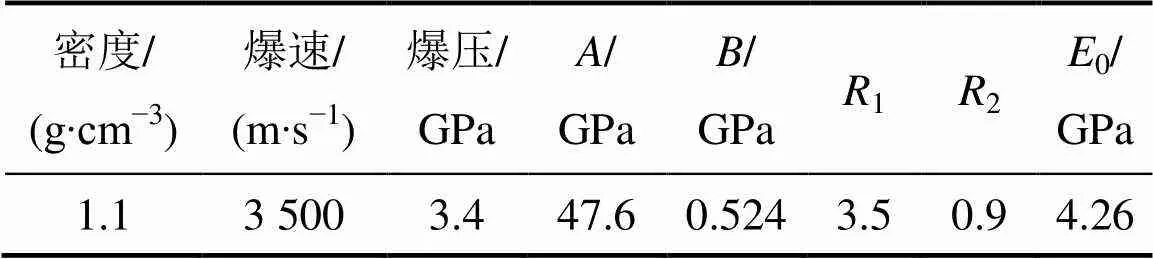
表4 炸药参数
2.3 数值模拟的可靠性分析
采用武汉中岩科技有限公司SR−VM2004便携式数据采集设备对地表振动进行监测,地表监测点与模型对应位置如图2所示。分析现场实测爆破振动数据,垂向峰值振动速度明显大于环向和径向峰值振动速度,垂向爆破振动速度对爆破地震效应起控制作 用[18−20],选择垂向振速作为评价爆破振动强度的物理量。
通道上方地表监测点垂向振动速度实测数据及对应的模拟结果如图3和图4所示。实测峰值振动速度为1.15 cm/s,模拟计算的峰值振动速度为1.20 cm/s,与实测值的绝对误差为0.05 cm/s,相对误差为4.35%,计算得到的振动速度波形与实测振动速度时程曲线的形态基本相同。因此,采用上述掏槽孔爆破模型对爆破产生的振动场进行模拟研究是可行的。
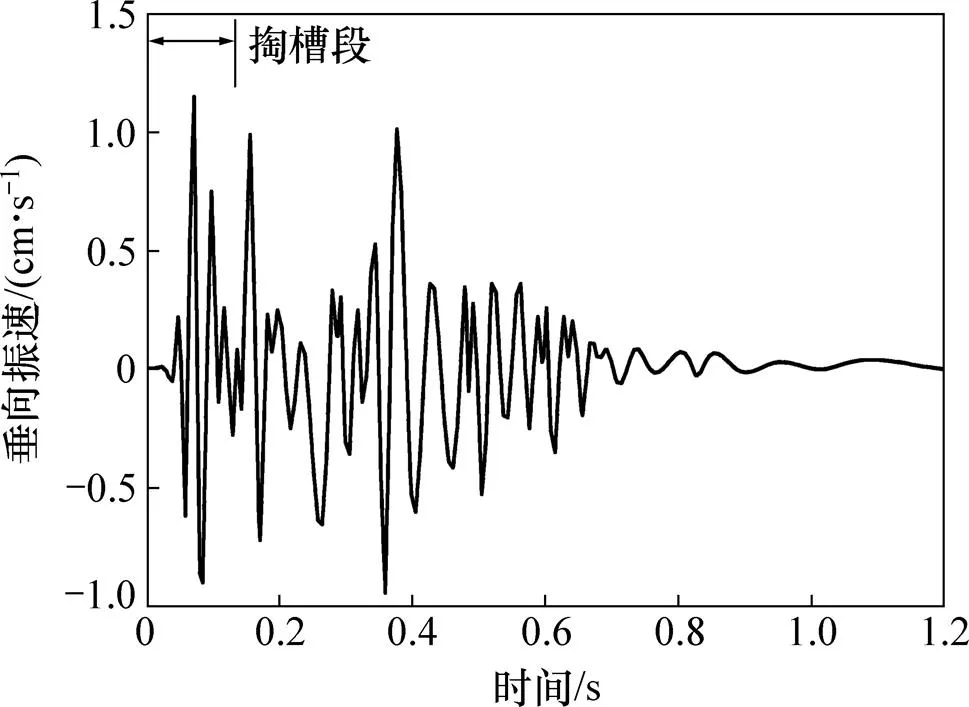
图3 垂向振动速度实测波形

图4 垂向振动速度模拟波形
3 不同工况下的数值模拟分析
对下台阶爆破开挖和全断面爆破开挖2种工况下沿通道开挖导洞轴向及垂直于通道开挖导洞轴向地表振动传播规律进行分析,监测点的布置方向如图5所示。
3.1 沿通道开挖导洞轴线方向地表振动传播规律
以掌子面中心正上方地表质点为原点,沿开挖导洞轴线方向距掌子面不同水平距离位置布置监测点,下台阶爆破开挖工况下各监测点垂向峰值振速如图6所示。图6中:横坐标负向表示掌子面后方(已开挖区域),横坐标正向表示掌子面前方(未开挖区域)。
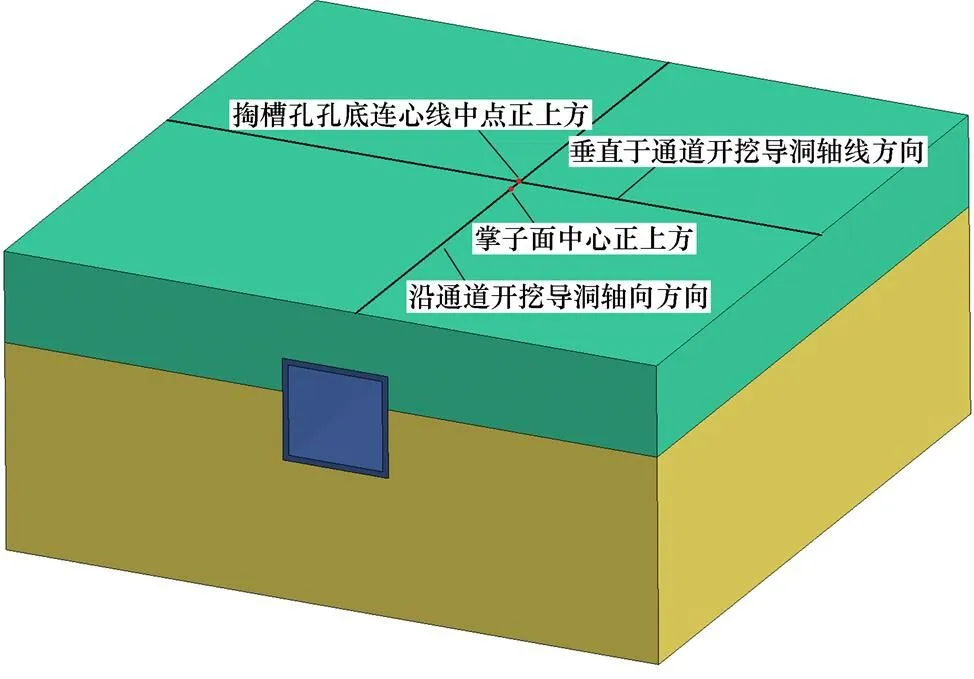
图5 地表监测点布置方向
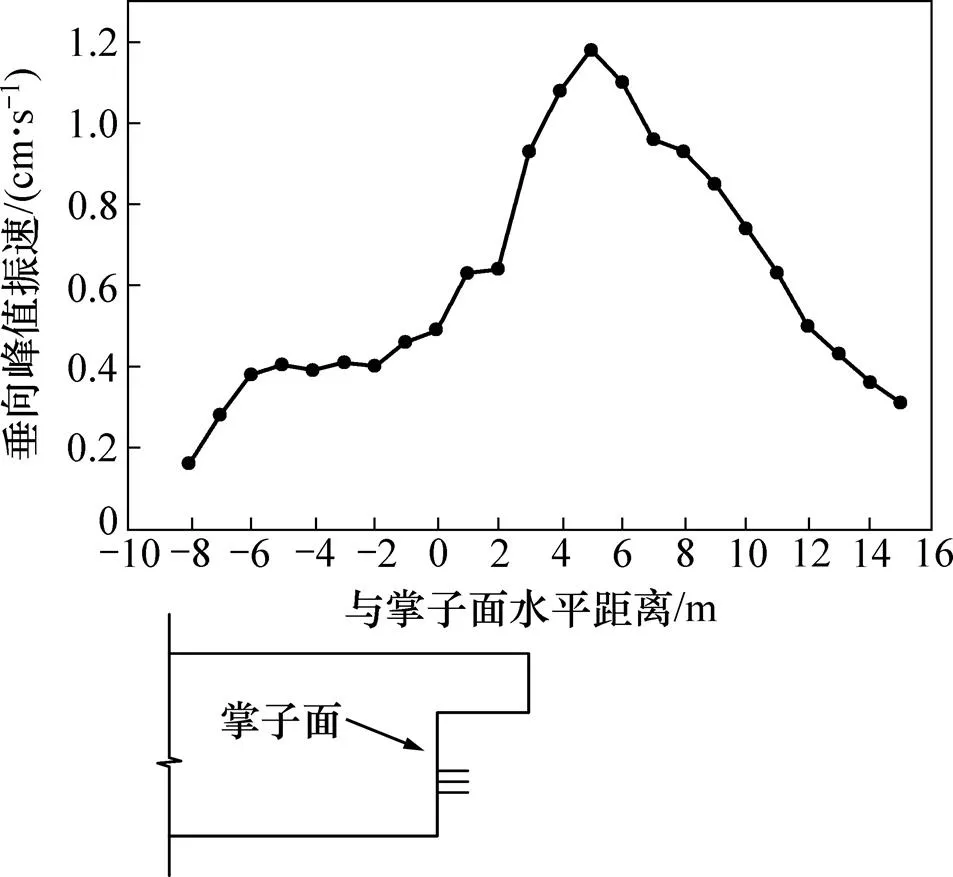
图6 下台阶爆破开挖各监测点垂向峰值振速
下台阶爆破开挖工况下,掌子面后方,随着与掌子面水平距离的增加,地表质点垂向峰值振速不断衰减,由于下部通道的存在,在−5~0 m范围内,应力波在地表与通道上表面之间反射叠加现象明显,使得地表质点垂向峰值振速衰减缓慢;在掌子面前方,由于通道上台阶粉质黏土的开挖,应力波传播过程中发生绕射,在0~5 m范围内,地表质点垂向峰值振速不断增大,掌子面前方5 m处速度达到最大值,掌子面前方地表质点垂向峰值振速整体呈现出先增大后减小的趋势。
分析通道全断面爆破开挖工况下开挖导洞轴向方向地表振动规律,并与下台阶爆破开挖工况进行对比,2种工况下各监测点垂向峰值振速对比如图7所示。
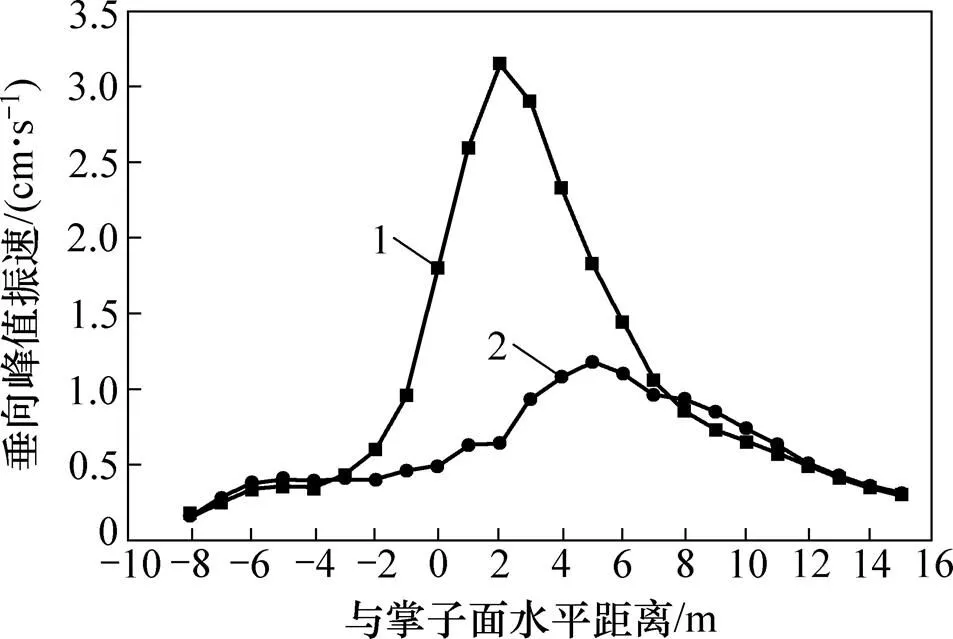
1—全断面爆破开挖;2—下台阶爆破开挖。
全断面爆破开挖工况下,掌子面后方,随着与掌子面水平距离的增加,地表质点垂向峰值振速不断衰减,且在−3~0 m范围内,地表质点垂向峰值速度衰减较快;在−6~−3 m范围内,由于下部通道的存在,应力波在地表与通道上表面之间反射叠加现象明显,使得地表质点垂向峰值振速衰减缓慢;掌子面前方2 m处地表质点垂向峰值振速达到最大,掌子面前方地表质点垂向振速整体呈现出先增大后减小的趋势。
从整体上来看,全断面爆破开挖地表质点垂向峰值振速分布规律与下台阶爆破开挖类似,从掌子面后方到掌子面前方,地表质点垂向峰值振速呈现出先增大后减小的趋势;在2种工况下,地表质点垂向峰值振速最大值出现在不同位置,全断面爆破开挖工况下,掌子面前方2 m处地表质点垂向峰值振速达到最大,在下台阶爆破开挖工况下,上台阶的开挖阻碍了应力波的传播,应力波发生绕射,掌子面前方5 m处地表质点垂向峰值振速达到最大;当掌子面前后方在距掌子面一定水平距离后,2种工况下地表质点垂向峰值振速大小和衰减情况大体一致;沿通道开挖导洞轴线方向,在全断面爆破开挖工况下,地表质点垂向峰值振速最大值为3.15 cm/s,下台阶爆破开挖工况下地表质点垂向峰值振速最大值为1.18 cm/s,可见上台阶的开挖阻隔了应力波的向上传播,能够有效降低地表质点垂向峰值振速;沿通道开挖导洞轴线方向,全断面爆破开挖工况下地表质点垂向峰值振速最大值是通道下台阶爆破开挖工况下的2.67倍。
3.2 垂直于通道开挖导洞轴线方向地表振动传播 规律
以掏槽孔孔底连心线中点正上方地表质点为原点,垂直于通道开挖导洞轴线方向选取一系列地表监测点,下台阶爆破开挖工况下各监测点垂向峰值振速如图8所示。图8中:横坐标负向表示通道开挖导洞轴线左侧区域,横坐标正向表示通道开挖导洞轴线右侧区域。
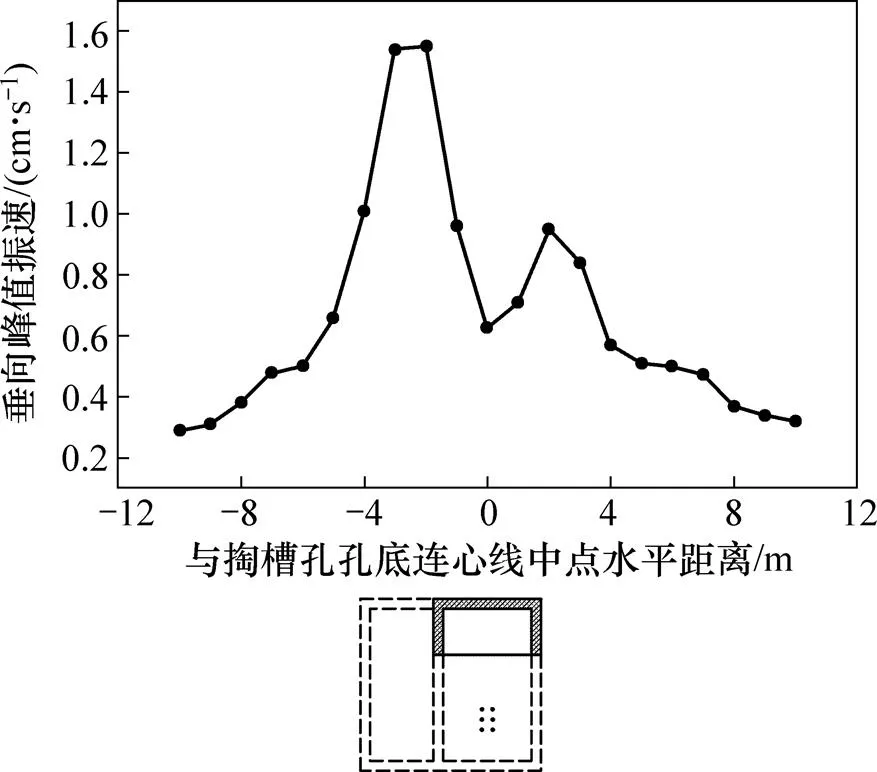
图8 下台阶爆破开挖各监测点垂向峰值振速
在下台阶爆破开挖工况下,垂直于通道开挖导洞轴线方向,由于通道上台阶粉质黏土的开挖,应力波在传播过程中发生绕射,掏槽孔孔底连心线中点正上方地表质点与爆源距离最小,但垂向峰值振速并不是最大,且在原点两侧2 m范围内,随着与原点水平距离的增加,垂向峰值振速不断增大;在原点两侧2 m范围外,随着与原点距离的增加,地表质点垂向峰值振速不断减小,且左侧地表质点垂向峰值振速衰减较右侧快;从垂向峰值振速曲线上来看,在原点两侧5 m范围内,距原点相同距离,左侧地表质点垂向峰值振速明显比右侧的大;当与原点距离超过5 m时,两侧地表质点垂向峰值振速差别不大。
分析通道全断面爆破开挖工况下垂直于通道开挖导洞轴线方向地表振动规律,并与下台阶爆破开挖工况进行对比,2种工况下各监测点垂向峰值振速对比如图9所示。
全断面爆破开挖工况下,垂直于通道开挖导洞轴线方向,掏槽孔孔底连心线中点正上方地表质点垂向峰值振速最大,左右两侧随着与原点距离的增加,地表质点垂向峰值振速不断减小;在原点两侧5 m范围内,对左右两侧距原点相同位置的地表质点垂向峰值振速进行比较可以发现:左侧地表质点垂向峰值振速明显大于右侧,左侧地表质点垂向峰值振速衰减较右侧缓,当与原点距离超过5 m时,两侧地表质点垂向峰值振速差别不大。

1—全断面爆破开挖;2—下台阶爆破开挖。
在全断面爆破开挖工况下,掏槽孔孔底连心线中点正上方地表质点垂向峰值振速最大,而在下台阶爆破开挖工况下,掏槽孔孔底连心线中点正上方地表质点与爆源距离最小,但垂向峰值振速并不是最大。对比结果验证了由于通道上台阶的开挖,应力波在垂直通道开挖导洞轴线方向传播时发生了绕射;当左右两侧在距原点一定距离后,2种工况下地表质点垂向振速的衰减情况趋于一致;垂直于通道开挖导洞轴线方向,在全断面爆破开挖工况下,地表质点垂向峰值振速最大为2.59 cm/s;在下台阶爆破开挖工况下,地表质点垂向峰值振速最大为1.55 cm/s,全断面爆破开挖工况下地表质点垂向峰值振速最大值是下台阶爆破开挖工况下的1.67倍。在2种工况下,在原点两侧5 m范围内,对左右两侧距原点相同位置处地表质点垂向峰值振速对比,左侧地表质点垂向峰值振速均明显比右侧的大,因此在CD法开挖时,垂直于通道开挖导洞轴线方向,要加强对后开挖导洞一侧的爆破振动监测。
4 结论
1) 模拟计算的峰值振动速度与实测值的绝对误差为0.05 cm/s,相对误差为4.35%,本计算模型可用于模拟掏槽孔爆破开挖。
2) 沿通道开挖导洞轴线方向,在下台阶爆破开挖工况下,由于应力波的绕射,掌子面前方5 m处地表质点垂向峰值振速达到最大值;全断面爆破开挖工况下(即上台阶粉质黏土不开挖),掌子面前方2 m处地表质点垂向峰值振速达到最大值。
3) 沿垂直于通道开挖导洞轴线方向,在下台阶爆破开挖工况下,掏槽孔孔底连心线中点正上方地表质点与爆源距离最小,但垂向峰值振速并不是最大,且在质点两侧2 m范围内,随着爆心距。的增加,垂向峰值振速不断增大;在全断面爆破开挖工况下,掏槽孔孔底连心线中点正上方地表质点垂向峰值振速最大,且随着爆心距。的增加,垂向峰值振速不断减小。
4) 上台阶的开挖阻隔了应力波的传播,能够有效降低地表质点垂向峰值振速。沿通道开挖导洞轴线方向,在全断面爆破开挖工况下,地表质点垂向峰值振速最大值是下台阶爆破开挖工况下的2.67倍;垂直于通道开挖导洞轴线方向,全断面爆破开挖工况下地表质点垂向峰值振速最大值是下台阶爆破开挖工况下的1.67倍。
[1] 朱泽兵, 张永兴, 刘新荣, 等. 特大断面车站隧道爆破开挖对地表建筑物的影响[J]. 重庆大学学报(自然科学版), 2010, 32(2): 110−116. ZHU Zebing, ZHANG Yongxing, LIU Xinrong, et al. Influence of blasting vibration on adjacent buildings of station tunnel[J].Journal of Chongqing University (Natural Science), 2010, 32(2): 110−116.
[2] 张永兴, 张远华. 隧道爆破开挖条件下地表建筑振动速度响应研究[J]. 地震工程与工程振动, 2010, 30(6): 112−119. ZHANG Yongxing, ZHANG Yuanhua. Research on vibration velocity response of surface building under the condition of blasting excavation in tunnel[J]. Journal of Earthquake Engineering and Engineering Vibration, 2010, 30(6): 112−119.
[3] 王伟. 爆破地震波影响下结构动力响应及其开裂规律研究[D]. 青岛: 青岛理工大学土木工程学院, 2014: 61−82.WANG Wei. Research on dynamic response and cracking under the laws of blasting seismic wave[D]. Qingdao: Qingdao Technological University. College of Civil Engineering, 2014: 61−82.
[4] 薛里, 施龙焱, 孙付峰. 地铁浅埋隧道爆破开挖振动控制研究[J]. 地下空间与工程学报, 2012, 8(4): 791−795+814. XUE Li, SHI Longyan, SUN Fufeng. Research on blasting vibration control of subway shallow tunnel excavation[J]. Chinese Journal of Underground Space and Engineering, 2012, 8(4): 791−795+814.
[5] 李付胜. 城市隧道掘进爆破数值模拟及震动效应控制研究[D]. 重庆: 重庆大学资源及环境科学学院, 2008: 97−105.LI Fusheng. Research of the numerical simulation for city tunnel excavation blasting seismic and the control of blasting vibration effects[D]. Chongqing: Chongqing University. College of Resource and Environment Science, 2008: 97−105.
[6] 高文学, 颜鹏程, 李志星, 等. 浅埋隧道爆破开挖及其振动效应研究[J]. 岩石力学与工程学报, 2011, 30(S2): 4153−4157. GAO Wenxue, YAN Pengcheng, LI Zhixing, et al. Blasting excavation and vibration effects of shallow tunnel excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S2): 4153−4157.
[7] 李利平, 李术才, 张庆松, 等. 浅埋大跨隧道现场试验研究[J]. 岩石力学与工程学报, 2007, 26(S1): 3565−3571. LI Liping, LI Shucai, ZHANG Qingsong, et al. In-situ testing study on shallow-buried large-span tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(S1): 3565−3571.
[8] 肖文涛, 肖文芳, 房泽法, 等. 地铁隧道掘进爆破地表震动效应研究[J]. 武汉理工大学学报, 2011, 33(10): 113−117. XIAO Wentao, XIAO Wenfang, FANG Zefa, et al. Study on vibration effects of ground induced by metro tunnel excavation blasting[J]. Journal of Wuhan University of Technology, 2011, 33(10): 113−117.
[9] 张继春, 曹孝君, 郑爽英, 等. 浅埋隧道掘进爆破的地表震动效应试验研究[J]. 岩石力学与工程学报, 2005, 24(22): 4158−4163. ZHANG Jichun, CAO Xiaojun, ZHENG Shuangying, et al. Experimental study on vibration effects of ground due to shallow tunnel blasting[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(22): 4158−4163.
[10] KUHLEMEYER R L, LYSMER J. Finite element method accuracy for wave propagation problems[J]. Journal of Soil Mechanics and Foundations Division, 1973, 99(5): 421−427.
[11] 许红涛. 岩石高边坡爆破动力稳定性研究[D]. 武汉: 武汉大学水资源与水利水电工程科学国家重点实验室, 2006: 49−68.XU Hongtao. Study on the dynamic stability of high rock slope induced by blasting vibration[D]. Wuhan: Wuhan University. State Key Laboratory of Water Resources and Hydropower Engineering Science, 2006: 49−68.
[12] 王鹏, 周传波, 耿雪峰, 等. 多孔同段爆破漏斗形成机理的数值模拟研究[J]. 岩土力学, 2010, 31(3): 993−997. WANG Peng, ZHOU Chuanbo, GENG Xuefeng, et al. Numerical simulation of formation mechanism of multi hole and same delay time for blasting crater[J]. Rock and Soil Mechanics, 2010, 31(3): 993−997.
[13] 蒋楠, 周传波. 爆破振动作用下既有铁路隧道结构动力响应特性[J]. 中国铁道科学, 2011, 32(6): 63−68. JIANG Nan, ZHOU Chuanbo. Dynamic response characteristic of existing railway tunnel structure subjected to blasting vibration[J]. China Railway Science, 2011, 32(6): 63−68.
[14] 曲树盛, 李忠献. 内爆炸作用下地铁车站结构的动力响应与破坏分析[J]. 天津大学学报, 2012, 45(4): 285−291. QU Shusheng, LI Zhongxian. Dynamic response and damage analysis of a subway station structure due to internal explosion[J]. Journal of Tianjin University, 2012, 45(4): 285−291.
[15] 马险峰, 隋涛, 尚金华, 等. 双圆盾构隧道在内部爆炸荷载下的响应分析[J]. 同济大学学报(自然科学版), 2011, 39(7): 983−988. MA Xianfeng, SUI Tao, SHANG Jinhua, et al. Response analysis of dot shield tunnels under internal explosion[J]. Journal of Tongji University (Natural Science), 2011, 39(7): 983−988.
[16] 郑爽英, 邹新宽. 下穿隧道爆破振动作用下石油管道的安全性评价[J]. 爆破, 2015, 32(2): 131−137. ZHENG Shuangying, ZOU Xinkuan. Safety evaluation of blasting vibration effect undercrossing tunneling on buried oil pipeline[J]. Blasting, 2015, 32(2): 131−137.
[17] YANG R, BAWDEN W F, KATSABANIS P D. A new constitutive model for blast damage[J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1996, 33(3): 245−254.
[18] 李玉民, 倪芝芳. 地下工程开挖爆破的地面振动特征[J]. 岩石力学与工程学报, 1997, 16(3): 75−79. LI Yumin, NI Zhifang. The characteristics on surface vibration of blasting in underground engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 1997, 16(3): 75−79.
[19] 翟才雅, 李安龙, 刘涛, 等. 花岗岩地区地铁隧道爆破振动传播规律研究[J]. 工程地质学报, 2014, 22(5): 824−831. ZHAI Caiya, LI Anlong, LIU Tao, et al. Vibration propagation of tunnel blasting in granite areas[J]. Journal of Engineering Geology, 2014, 22(5): 824−831.
[20] 丁雄, 阳生权, 林平, 等. 轻轨隧道开挖引起的爆破振动特性分析[J]. 铁道科学与工程学报, 2015, 12(3): 590−595. DING Xiong, YANG Shengquan, LIN Ping, et al. Analysis of the blasting vibration characteristics during light rail tunneling[J]. Journal of Railway Science and Engineering, 2015, 12(3): 590−595.
(编辑 陈爱华)
Propagation characteristics of ground vibration induced by subsurface blasting excavation in an ultra-shallow buried underpass
ZHANG Zhen, ZHOU Chuanbo, LU Shiwei, WU Chao, WANG Chao
(Faculty of Engineering, China University of Geosciences, Wuhan 430074, China)
Combined with the blasting excavation of an ultra-shallow buried underpass in Wuhan Metro Line 2, field monitoring of blasting vibration and numerical simulation were used to study the propagation law of ground vibration induced by the blasting excavation of the lower bench. In order to investigate the influence of the upper bench to the propagation characteristic of blasting seismic wave, the propagation law of ground vibration induced by the blasting excavation of the full section was also studied by numerical simulation. The results show that in the condition of the blasting excavation of the lower bench, the maximum ground PPV reaches at 5 m ahead of working face along the axis of pilot because of the wave diffraction. In the direction normal to the axis of pilot, the maximum ground PPV does not occur at the point right above the center of cut holes’ bottom, although it is the closest to explosion source, and within the range of 2 m away from the aforementioned point, the ground PPV increases continuously with an increasing distance to explosion source. Under the condition of the blasting excavation of the full section, the maximum ground PPV reaches at 2 m ahead of working face along the axis of pilot; the maximum ground PPV reaches at the point which is on the ground right above the center of cut holes’ bottom in the direction normal to the axis of pilot, and the ground PPV decreases continuously with an increasing distance to explosion source. Comparing the ground vibration in the above 2 conditions, the excavation space of the underpass’s upper bench hinders the propagation of stress wave, and can lower the ground PPV effectively.
underpass; blasting excavation; numerical simulation; ground vibration; propagation law
10.11817/j.issn.1672−7207.2017.08.020
U455.6
A
1672−7207(2017)08−2119−07
2016−09−07;
2016−12−28
国家自然科学基金资助项目(41372312,51379194);黄鹤英才(科技)计划项目(2015055003);中国博士后科学基金资助项目(2015T80854)(Projects(41372312, 51379194) supported by the National Natural Science Foundation of China; Project(2015055003) supported by the Huanghe Yingcai (Science and Technology) Program; Project (2015T80854) supported by the China Postdoctoral Science Foundation)
周传波,博士,教授,从事岩土工程、工程爆破方面的研究;E-mail:cbzhou@cug.edu.cn

