基于串级ADRC的四旋翼飞行器悬停控制
叶孝璐,俞立,张文安,张丹
基于串级ADRC的四旋翼飞行器悬停控制
叶孝璐,俞立,张文安,张丹
(浙江工业大学信息工程学院,浙江杭州,310023)
针对四旋翼悬停控制问题,提出一种串级自抗扰控制方法。首先,根据欧拉及牛顿定理建立四旋翼飞行器的动力学模型,并解耦为双回路、多子系统的结构。其次,根据四旋翼飞行器系统的自身结构特点,设计串级自抗扰控制器,为获取较好的内环输入信号,对外环设计线性ADRC控制器;同时,设计内环非线性ARDC控制器以获得更好的跟踪性能。针对系统内部参数摄动和存在外部干扰等不确定性,引入扩张状态观测器对系统的状态和内外扰动进行实时估计,并利用非线性误差反馈控制律进行补偿,消除内外扰动的影响。最后,仿真验证所提控制策略的有效性和优越性。
四旋翼飞行器;串级自抗扰算法;扩张状态观测器;悬停控制
四旋翼飞行器具有广阔的民用和军用前景[1−2],近些年已受到国内外研究学者广泛关注[3−5]。四旋翼飞行器是一个四输入六输出的欠驱动、非线性、强耦合系统[6−7],给控制器的设计带来了很大困难。另外,其动力学模型的复杂性、参数不确定性和建模过程中简化导致建模不精确等问题[8−9],对其控制器的鲁棒性、抗干扰性提出了较高的要求[10−11]。针对四旋翼飞行器悬停控制问题,目前使用的方法主要有PID控制[12]、反步控制[13]、嵌套饱和控制[14]等。基于PID的四旋翼飞行器悬停控制器将控制系统分为几个独立的通道,分别设计相应的PID控制算法,该方法具有控制技术成熟、易于实现的特点,但是其抗干扰性较差,如环境改变即要重新调整参数。基于反步法的四旋翼飞行器悬停控制器通过系统的状态方程设计虚拟控制,构造合适的Lyapunov函数来求控制律,具有良好的跟踪性能、且具有无超调、调节时间快的优点,但是该方法针对满足严格反馈控制结构的系统,对系统要求高。基于嵌套饱和的四旋翼飞行器悬停控制具有计算量小、鲁棒性强和全局渐近稳定的优点,但是应用该方法需要将四旋翼动力学模型转化为严格的前馈级联结构,而针对四旋翼飞行器这种欠驱动系统只能局部反馈线性化,不能完全反馈线性化。针对以上问题,本文作者提出用自抗扰算法来解决四旋翼飞行器的悬停控制问题,该算法比反步法和嵌套饱和算法对系统模型的要求低,而对扰动的抑制能力和控制精度又比PID算法高。针对存在内部未建模项和存在外部干扰等不确定性的四旋翼飞行器系统,本文作者将系统解耦为双回路、多子系统的结构,并提出了一种串级自抗扰控制方法,引入扩张状态观测器对系统的状态和内外扰动进行实时估计,并利用非线性误差反馈控制律进行补偿,降低了对模型精度的要求,消除内外扰动的影响。基于串级ADRC的四旋翼飞行器悬停控制器外环为位置环,内环为姿态环,外环ADRC控制器输出的控制量为内环的输入。为获得较平缓的外环控制输出,外环采用线性ADRC控制器;为得到更好的跟踪效果,在内环设计非线性ADRC控制器。最后通过仿真验证所设计控制器的有效性和优越性。
1 问题的描述
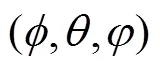
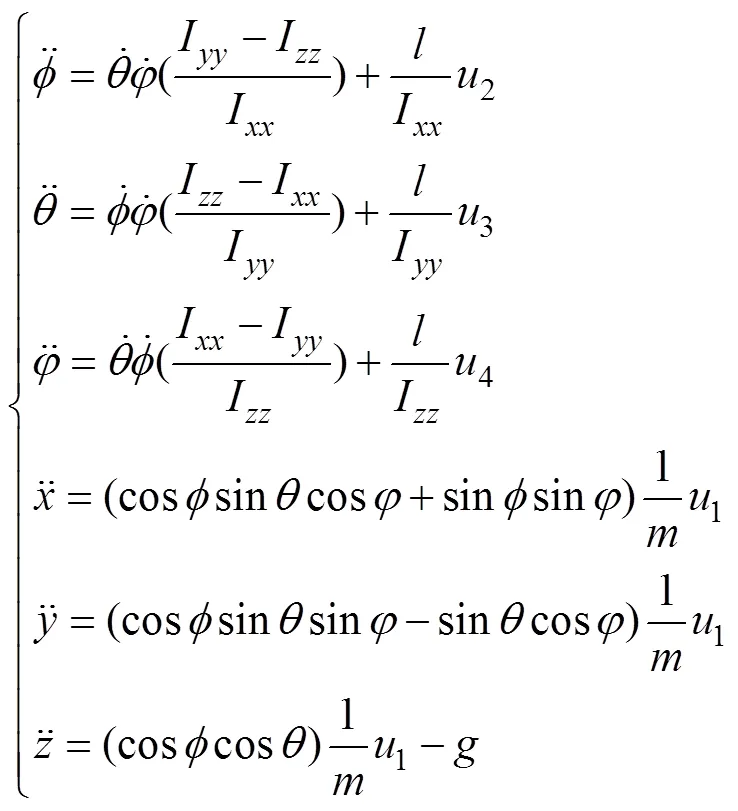
对螺旋桨的角速度的控制量为

其中:为四旋翼飞行器的质量;为四旋翼的旋翼臂展;I,I和I分别为轴、轴和轴的惯量;1,2,3和4为螺旋桨的角速度;为推力系数;为阻力系数。
选择状态向量为
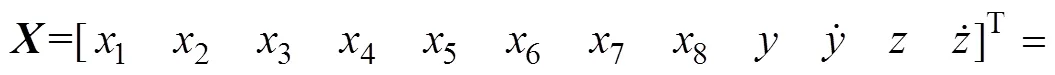
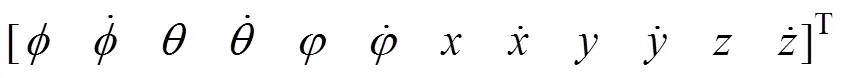
则可将式(1)表示为状态空间模型:
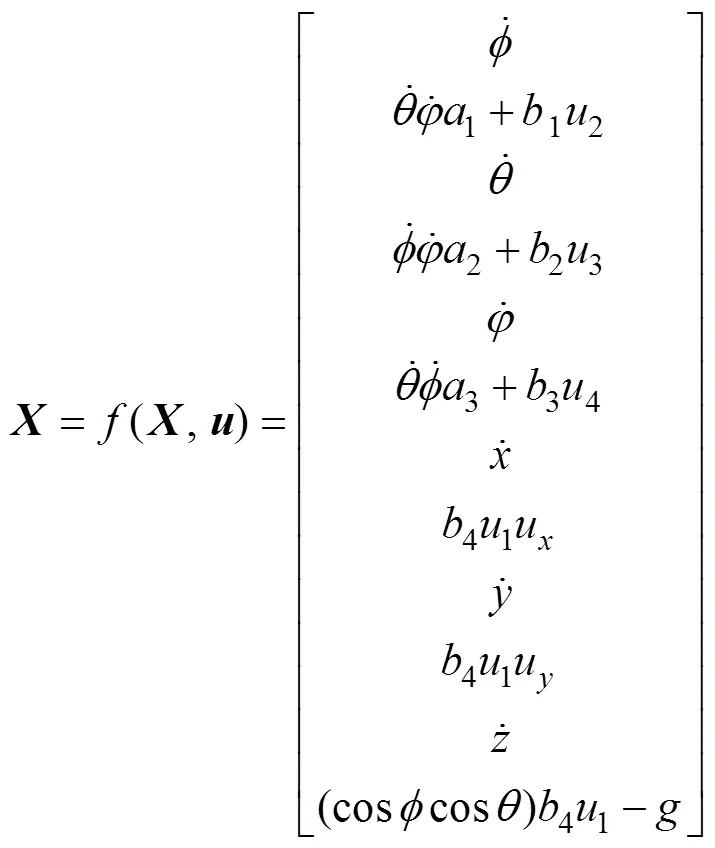
根据其建模动力学方程双回路、多子系统的结构的特点,可以将悬停控制器设计为串级结构,内环为姿态环,外环为位置环。并根据ADRC算法比反步法和嵌套饱和算法对系统模型的要求低,而对扰动的抑制能力和控制精度又比PID算法高的优点。本文提出串级自抗扰控制器来解决四旋翼飞行器的悬停问题,内环和外环均采用自抗扰算法[19]设计控制器,偏航角采用ADRC控制器进行锁定,四旋翼飞行器串级ADRC控制框图如图1所示。
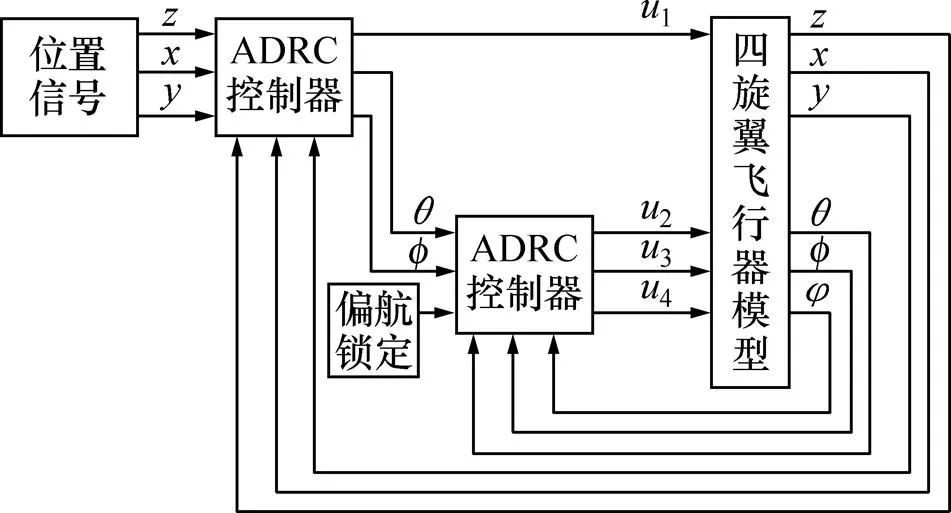
图1 四旋翼飞行器串级ADRC控制框图
2 串级ADRC控制器设计
2.1 外环控制器设计
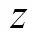
1) 跟踪微分器,用来安排过渡过程,给定信号0作为参考输入:
其中:参数0为跟踪微分器的快速因子。
2) 扩张状态观测器,对系统的状态和扰动进行实时估计与补偿。
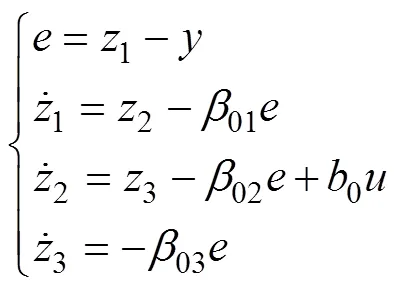
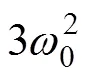
3) 状态误差反馈控制律:
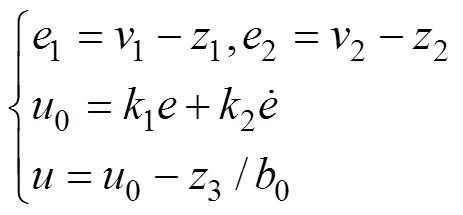
式中:k1和k2分别为比例和微分系数,可以通过极点配置取,。
2.2 内环控制器设计
四旋翼飞行器的内环为姿态环,分为3个独立的控制回路:横滚角控制回路、俯仰角控制回路和偏航角控制回路。四旋翼飞行器内环的非线性ADRC的控制框图如图3所示。
自抗扰控制器包括跟踪微分器、扩张状态观测器、状态误差反馈控制律3个部分。其设计过程如下。
1) 安排过渡过程,给定信号0作为参考输入。
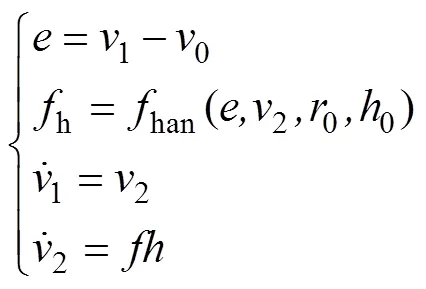
2) 扩张状态观测器,对系统的状态和扰动进行实时估计与补偿。
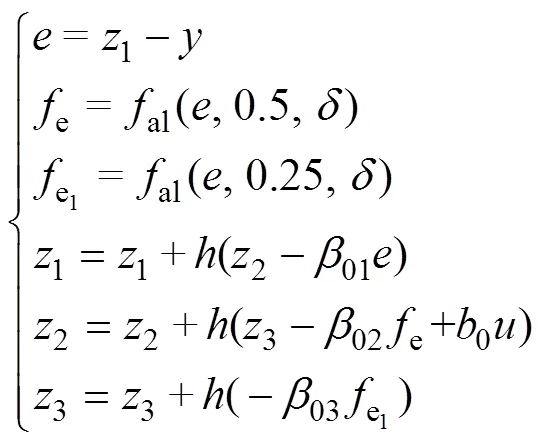
3) 状态误差反馈控制律:
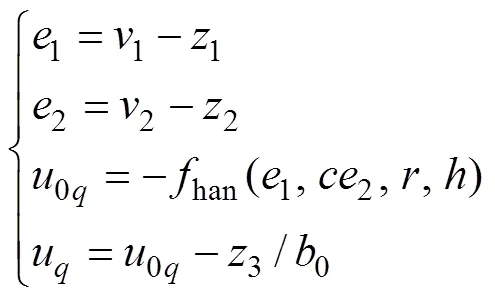


3 仿真结果
在Matlab/Simulink环境搭建四旋翼飞行器仿真控制系统,四旋翼无人机仿真参数如表1所示[20]。串级ADRC控制器的内环和外环仿真参数如表2和3所示。其中:轴的微分跟踪器为非线性,0=0.001;轴的扩张状态观测器为非线性,=0.01。
图4所示为四旋翼飞行器的飞行轨迹曲线。当四旋翼飞行器从地面坐标系位置(0,0,0)飞至目标位置(1,1,3)时,设定仿真时间为3 s,使得四旋翼飞行器悬停在(1,1,3)处。由图4可见:采用串级ADRC控制器的四旋翼飞行器能够快速平稳地飞向目标位置并悬停于目标位置,控制效果良好。
串级ADRC控制器的外环为位置环。本文在仿真实验中得出,若外环设计非线性ADRC控制器,则控制器输出的控制量信号为幅值很大高频噪声信号,而这类外环控制器输出的控制量是不满足要求的,其原因是:1) 外环的控制器输出作为内环输入的目标跟踪信号,而内环控制器无法跟踪高频信号。2) 外环的控制器输出即是四旋翼飞行器的3个姿态角,其实信号的幅值太大,在实际情况中,四旋翼飞行器早已翻滚坠机而失控。
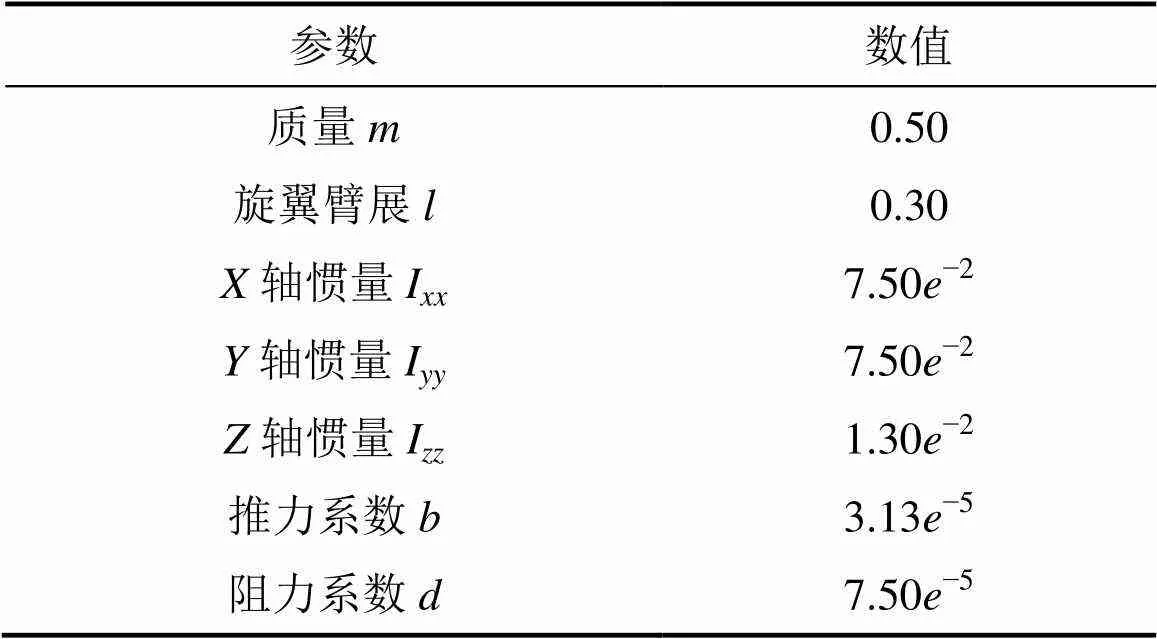
表1 四旋翼无人机的仿真参数
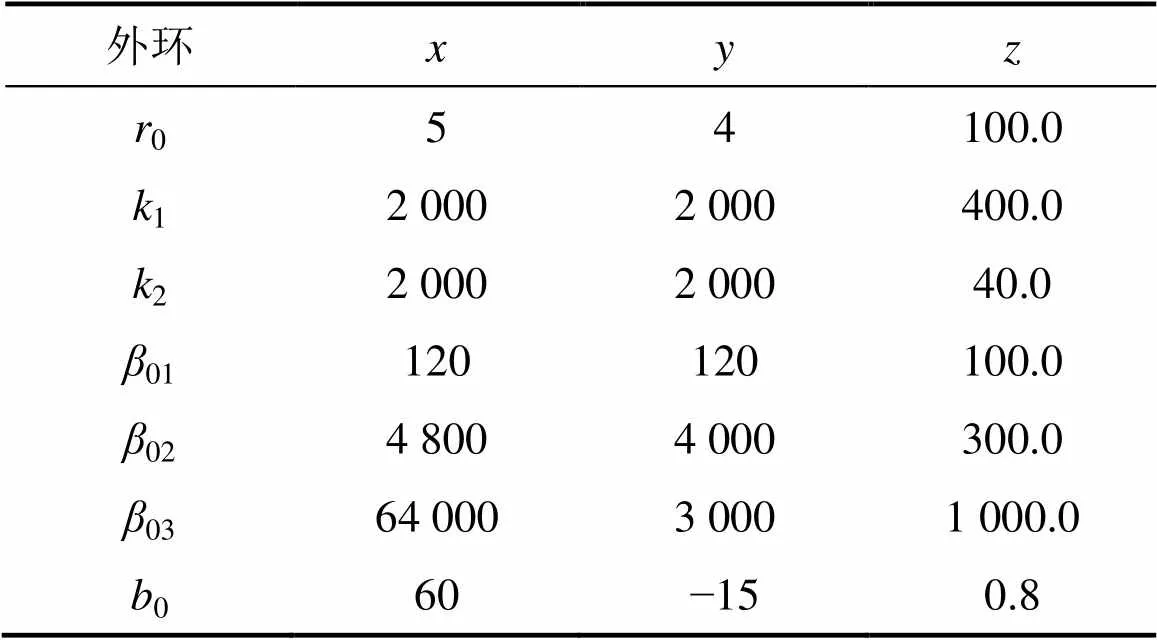
表2 四旋翼无人机的外环仿真参数
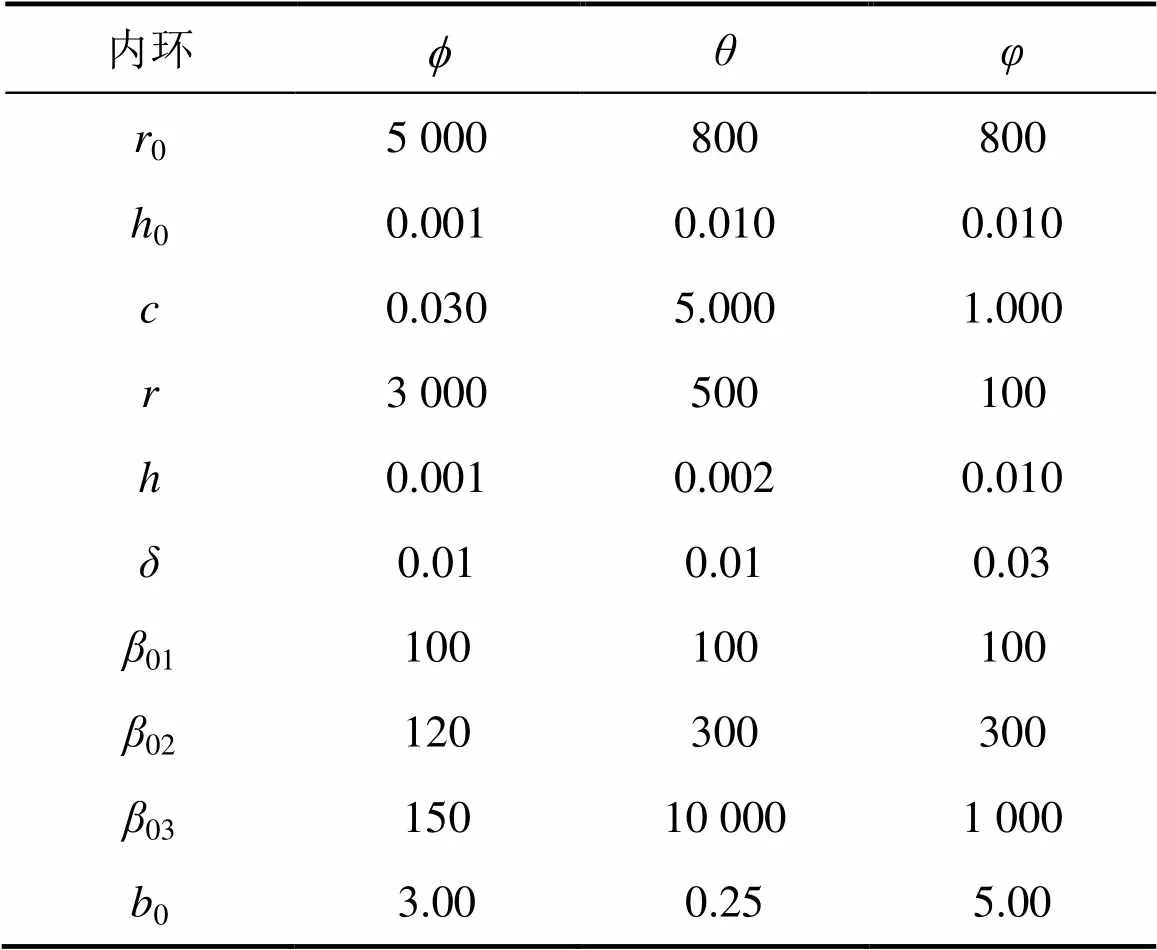
表3 四旋翼无人机的内环仿真参数
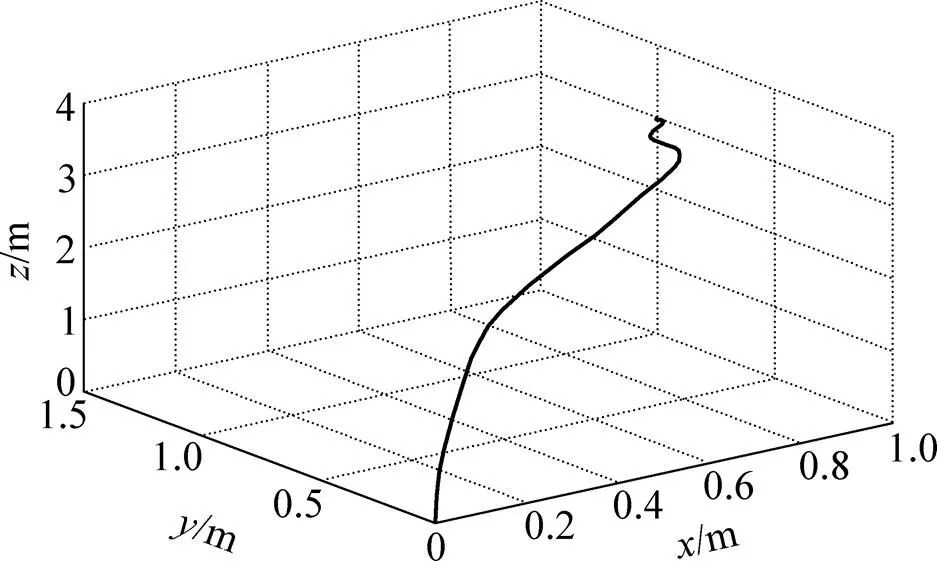
图4 四旋翼飞行器的飞行轨迹曲线
因此,为获取较好内环输入的跟踪信号(即外环ADRC输出的控制信号),外环的ADRC控制器为线性ARDC控制器,TD、状态误差反馈控制律、ESO均为线性。而为获取更好的跟踪效果,内环(姿态环)采用非线性ADRC控制器,TD、状态误差反馈控制律、ESO均为非线性。
图5所示为串级ADRC控制器外环跟踪曲线。实线为目标位置,虚线为跟踪轨迹,,和3个轴向均可在1.5 s内跟踪上给定信号。
图6所示为串级ADRC控制器内环跟踪曲线。实线为外环ADRC控制器输出的控制量即为内环的输入量,虚线内环的跟踪曲线。可见非线性ARDC控制具有很好的轨迹跟踪能力,偏航角为偏航锁定,可见ADRC控制器具有良好的四旋翼偏航锁定性能。基于串级ARDC的四旋翼飞行器悬停控制器优点不仅在于对系统模型的要求低,控制精度高,更重要的是其对扰动的抑制能力。图7~9所示为加入高频白噪声之后,串级ADRC和串级PID的控制效果对比。

(a) x轴位移−时间曲线;(b) y轴位移−时间曲线;(c) c轴位移−时间曲线
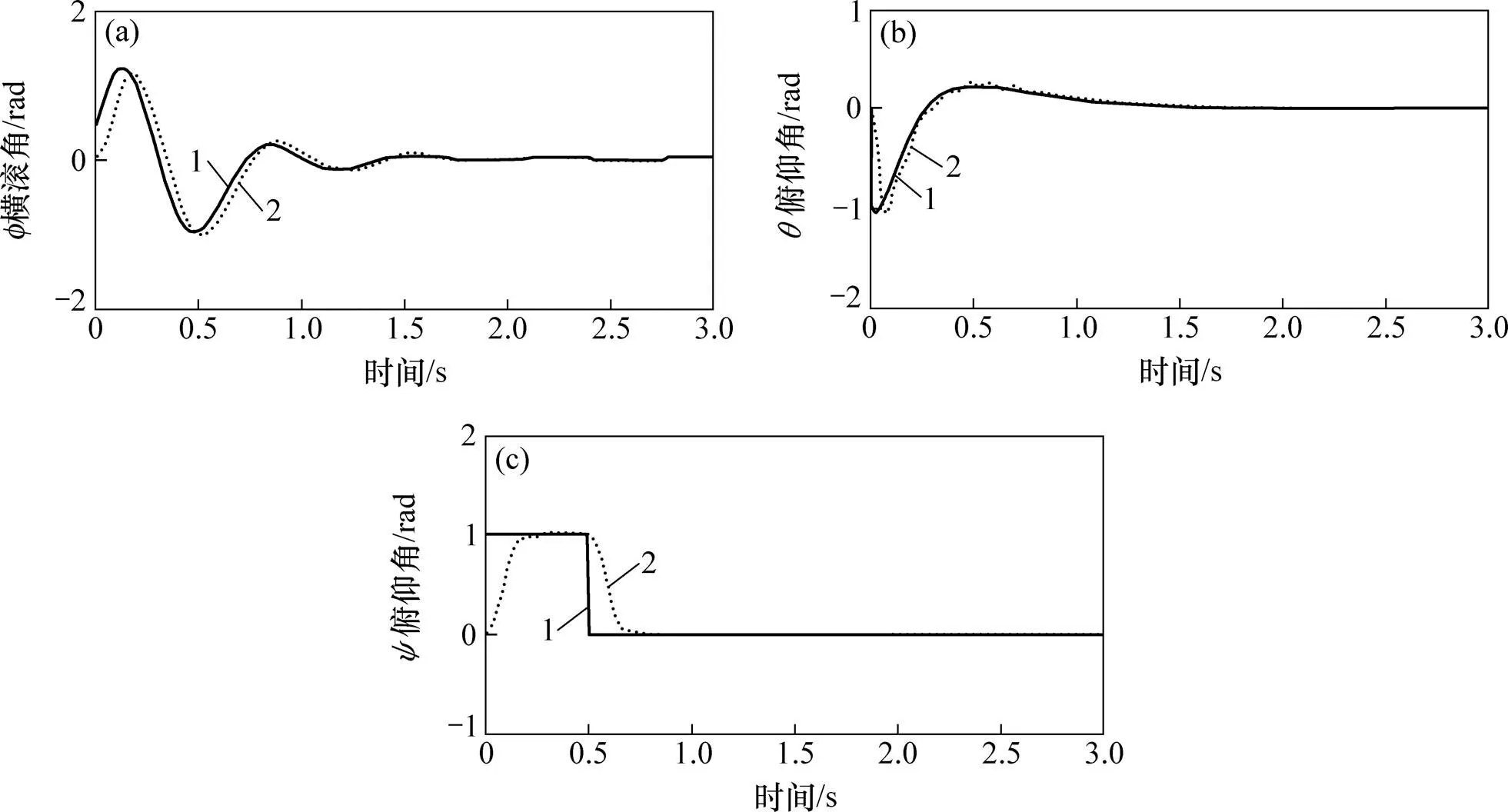
(a) f横滚角−时间曲线;(b) θ俯仰角−时间曲线;(c) ψ俯仰角−时间曲线
图7所示为有噪声输入控制器外环跟踪曲线对比。由图7可见:加入高频的白噪声后,ADRC控制的控制效果比PID的控制效果更好,在1.5 s内到达稳态,调节时间短且超调量小。而PID控制器在高频噪声的干扰下,调节时间变长,出现了稳态误差。并与图5相比可得有无高频噪声情况下,串级ADRC的跟踪曲线一致,可见ADRC中的扩张状态观测器可以很好地对扰动进行估计,并利用非线性误差反馈控制率进行补偿,消除了高频噪声扰动的影响。由图8和图9可得:在调节时间一致的情况下,外环ADRC控制器输出的控制量比PID控制器输出的控制量变化更缓和,非线性ADRC内环跟踪器的跟踪速度更快,误差更小。由此可见,本文所提串级ADRC算法比反步法和嵌套饱和法对模型的要求更低,而对扰动的抑制能力比串级PID算法的强,控制精度又比串级PID算法的高。

(a) x轴位移−时间曲线;(b) y轴位移−时间曲线;(c) z轴位移−时间曲线

(a) f横滚角−时间曲线;(b) θ俯仰角−时间曲线;(c) ψ俯仰角−时间曲线
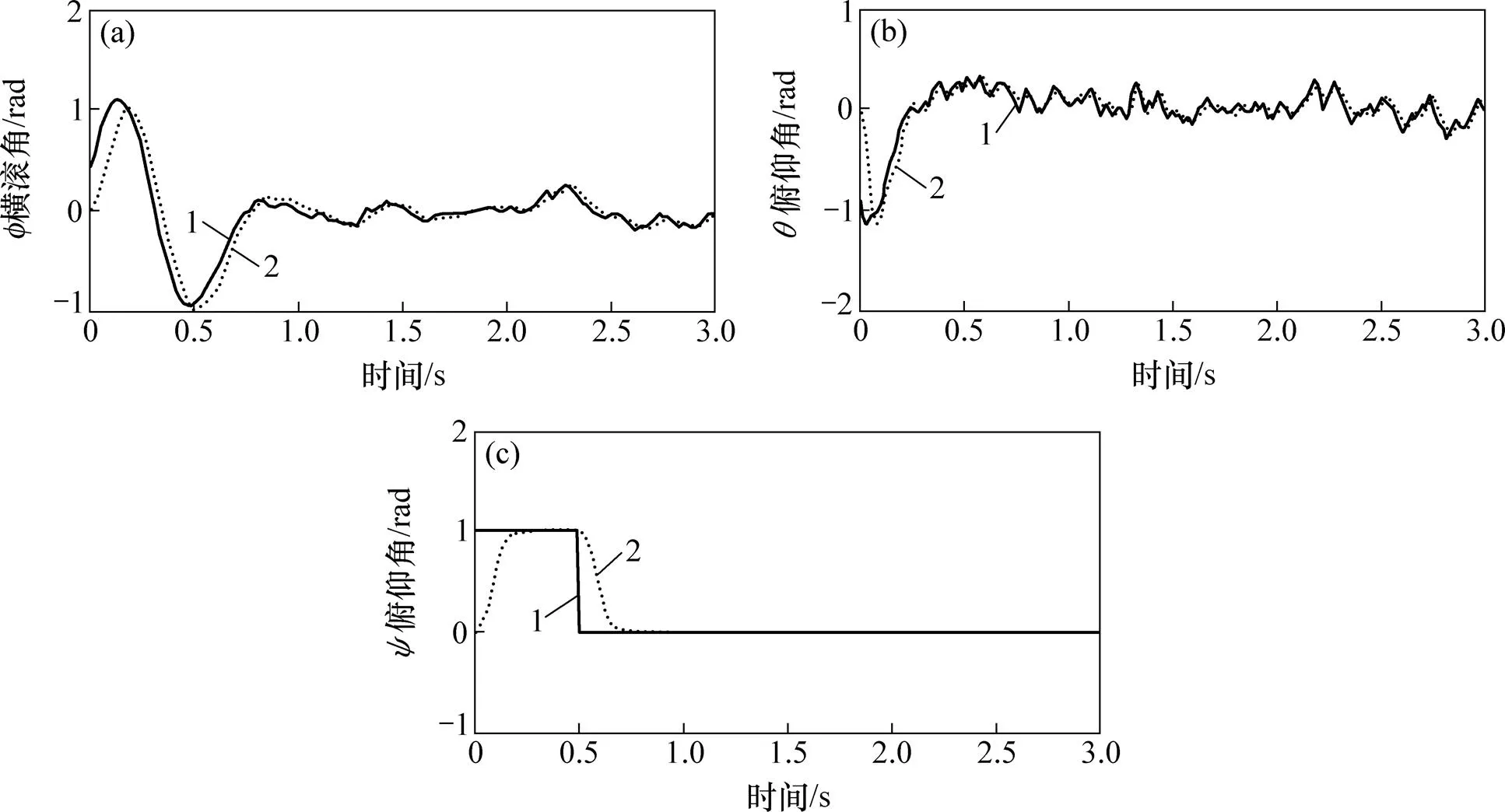
1—目标位置;2—跟踪曲线。
4 结论
1) 针对一类具有多输入多输出强耦合的不确定非线性四旋翼飞行器控制系统,提出了一种串级自抗扰控制方法。将系统解耦为双回路、多子系统的结构,针对所控制需求不同,对外环设计线性ADRC控制器,内环设计非线性ADRC控制,内外环均引入扩张状态观测器对系统的状态和内外扰动进行实时估计,并利用非线性反馈控制律进行补偿,消除内外扰动的影响。
2) 所设计的串级自抗扰控制器在系统存在不确定和内外扰动的情况下,仍能够实现四旋翼飞行器的悬停控制,且具有良好的性能指标和鲁棒性。
[1] PHANG S K, CAI C, CHEN B M, et al. Design and mathematical modeling of a 4-standard-propeller (4sp) quadrotor[C]//2012 10th World Congress on Intelligent Control and Automation. Beijing: IEEE, 2012: 3270−3275.
[2] ABDESSAMEUD A, TAYEBI A. Global trajectory tracking control of VTOL-UAVs without linear velocity measurements[J]. Automatica, 2010, 46(6): 1053−1059.
[3] DYDEK Z T, ANNASWAMY A M, LAVRETSKY E. Adaptive control of quadrotor UAVs: a design trade study with flight evaluations[J]. IEEE Transactions on Control Systems Technology, 2013, 21(4): 1400−1406.
[4] 曾小勇, 彭辉, 吴军. 四旋翼飞行器的建模与姿态控制[J]. 中南大学学报(自然科学版), 2013, 44(9): 3693−3700. ZENG Xiaoyong, PENG Hui, WU Jun. Modeling and attitude control for a quad-rotor aircraft[J]. Journal of Central South University (Science and Technology), 2013, 44(9): 3693−3700.
[5] GRZONKA S, GRISETTI G, BURGARD W. A fully autonomous indoor quadrotor[J]. IEEE Transactions on Robotics, 2012, 28(1): 90−100.
[6] MAHONY R, KUMAR V, CORKE P. Multirotor aerial vehicles: modeling, estimation, and control of quadrotor[J]. IEEE Robotics & Automation Magazine, 2012, 19(3): 20−32.
[7] RYLL M, BULTHOFF H H, GIORDANO P R. Modeling and control of a quadrotor UAV with tilting propellers[C]//2012 IEEE International Conference on Robotics and Automation. Saint Paul: IEEE, 2012: 4606−4613.
[8] TANVEER M H, AHMED S F, HAZRY D, et al. Stabilized controller design for attitude and altitude controlling of quad-rotor under disturbance and noisy conditions[J]. American Journal of Applied Sciences, 2013, 10(8): 819−831.
[9] KUSHLEYEV A, MELLINGER D, POWERS C, et al. Towards a swarm of agile micro quadrotors[J]. Autonomous Robots, 2013, 35(4): 287−300.
[10] NICOL C, MACNAB C J B. RAMIREZ-SERRANO. Robust adaptive control of a quadrotor helicopter[J]. Mechatronics, 2011, 21(6): 927−938.
[11] RYAN T, KIM H J. LMI-based gain synthesis for simple robust quadrotor control[J]. IEEE Transactions on Automation Science and Engineering, 2013, 10(4): 1173−1178.
[12] 李一波, 宋述锡. 基于模糊自整定PID四旋翼无人机悬停控制[J]. 控制工程, 2013, 20(5): 910−914. LI Yibo, SONG Shuxi. Hovering control for quadrotor unmanned helicopter based on fuzzy self-tuning PID algorithm[J]. Control Engineering of China, 2013, 20(5): 910−914.
[13] AZINHEIRA J R, MOUTINHO A. Hover control of an UAV with backstepping design including input saturations[J]. IEEE Transactions on Control Systems Technology, 2008, 16(3): 517−526.
[14] ZAMUDIO Z, LOZANO R, TORRES J, et al. Vision based stabilization of a quadrotor using nested saturation control approach[C]//2011 15th International Conference on System Theory, Control, and Computing. Sinaia: IEEE, 2011: 1−6.
[15] 李俊, 李运堂. 四旋翼飞行器的动力学建模及PID控制[J]. 辽宁工程技术大学学报(自然科学版), 2012, 31(1): 114−117. LI Jun, LI Yuntang. Modeling and PID control for a quadrotor[J]. Journal of Liaoning Technical University (Natural Science), 2012, 31(1): 114−117.
[16] 吴成富, 刘小齐, 马松辉. 四旋翼无人机建模及其四元数控制律设计[J]. 飞行力学, 2013, 31(2): 122−125. WU Chengfu, LIU Xiaoqi, MA Songhui. Modeling and control for a quadrotor UAV based on quaternion[J]. Flight Dynamics, 2013, 31(2): 122−125.
[17] 韩志凤, 李荣冰, 刘建业, 等. 小型四旋翼飞行器动力学模型优化[J]. 控制工程, 2013, 20(增刊): 158−162. HAN Zhifeng, LI Rongbing, LIU Jianye, et al. Model optimization of small quad-rotor in the case of center of mass offset[J]. Control Engineering of China, 2013, 20(Suppl): 158−162.
[18] 陈航科, 张东升, 盛晓超, 等. 四旋翼飞行器悬停状态姿态控制建模与仿真[J]. 计算机仿真, 2013, 30(11): 41−45. CHEN Hangke, ZHANG Dongsheng, SHENG Xiaochao, et al. Modeling and attitude control simulation for four-rotor aircraft in hover[J]. Computer Simulation, 2013, 30(11): 41−45.
[19] 韩京清. 自抗扰控制技术−估计补偿不确定因数[M]. 北京: 国防工业出版社, 2008: 212−238. HAN Jingqing. Active disturbance rejection control technique-the technique for estimating and compensating the uncertainties[M]. Beijing: National Defense Industry Press, 2008: 212−238.
[20] 张益鹏. 四旋翼无人机自适应控制与故障容错[D]. 南京: 南京邮电大学, 2014: 37−45. ZHANG Yipeng. Adaptive control and fault tolerant of quadrotor unmanned aerial vehicles[M]. Nanjing: Nanjing University of Posts and Telecommunications, 2014: 37−45.
(编辑 陈爱华)
Cascade ADRC-based hover control for quadrotor air vehicles
YE Xiaolu, YU Li, ZHANG Wenan, ZHANG Dan
(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China)
A cascade active disturbance rejection controller was designed for the hover control of a quadrotor air vehicle. First, a dynamic model of a quadrotor air vehicle was presented by applying the Euler and Newton theorem, where the model was further decoupled as a double loops and multi-subsystems structure. Then, a cascade active disturbance rejection controller (ADRC) was designed by taking the structural features of quadrotor air vehicle systems into consideration. A linear ADRC controller was designed for the external-loop to obtain a better loop input signal and a nonlinear ARDC controller was deisgned for the inner-loop to obtain better tracking performance. For the parameter perturbations within the system and the influence of the existing uncertainties of external disturbances, an extended state observer was designed for estimating the state and the sum of internal and external disturbance of the system, and the nonlinear state error feedback control law was used upon this to compensate the disturbance and eliminate the influence of internal and external disturbance on the system. Finally, simulations were presented to verify the effectiveness and superiority of the proposed control method.
quadrotor air vehicle; cascade active disturbance rejection controller (ADRC); extended state observer; hover control
10.11817/j.issn.1672−7207.2017.08.015
TP319;V249.1
A
1672−7207(2017)08−2079−09
2016−09−18;
2016−12−22
国家自然科学基金资助项目(61273117,61673351);浙江省自然科学基金重点资助项目(2014R403087)(Projects(61273117, 61673351) supported by the National Natural Science Foundation of China; Project(2014R403087) supported by Zhejiang Provincial Natural Science Foundation of China)
俞立,博士,教授,从事网络化控制、机器人控制的研究;E-mail:lyu@zjut.edu.cn

