小学数学教学中数形结合的运用

程小爱

（永修县新城小学，江西九江 330304）

小学数学教学中数形结合的运用

程小爱

（永修县新城小学，江西九江 330304）

数学是研究客观世界的数量关系和空间形式的科学。同一个客观事物所具有的数和形的属性相互联系，又在一定的条件下相互转化。利用这种转化，使数形结合，有利于数学问题化难为易。数形结合的方法在小学数学教学中有广泛的应用。做到数形结合能启迪学生的思维，有效提高学生解决问题的能力。

小学数学；数形结合

一、运用数形结合揭示概念本质

概念是人们反映事物本质属性的思维形式，正确理解概念和运用概念是提高学生思维能力的基础。学生学习概念的过程是一个复杂的思维过程，教学中教师应注重在感性认识的基础上，采用数形结合，通过比较、分析和综合，抽取概念的本质，从而全面明确概念，掌握概念的本质特征。

案例1：《倍的认识》教学片断（多层练习完善“倍”的认识）

1.摆圆片

现在，请孩子们拿出6个圆片，摆成上下2行，使两行的圆片数量成倍数关系。请轻轻地拿出学具摆一摆。

交流：第一行摆几个，第二行摆了几个几，谁是谁的几倍？

2.拍手游戏

孩子们，你们刚才的表现可真棒！老师也忍不住要为你们鼓掌。（老师拍3下）提问：谁听清楚了，刚才老师拍了几下？谁能拍出老师的2倍？要让大家清晰地听出2倍的关系，注意停顿。提问：老师拍了3下，你拍了几个几下？他拍对了吗？孩子们，你们会拍了吗？听好了（老师拍2下）请拍出我的3倍。（老师拍4下）请拍出我的2倍。谁来当小老师拍一拍？

3.创造一幅“2倍”关系图

孩子们，接下来我们来进行一个小小设计师的比拼，请各位小设计师们发挥想象，创造一幅2倍关系图，注意要求：一个数量是另一个数量的2倍。请拿出纸和笔画一画，看谁创造的图既准确又美观。学生画完后投影展示学生作品。提问：你画了什么？谁是谁的几倍？

刚才大家创造出了这么多2倍关系的图，真棒！能不能用一个图表示所有的2倍关系呢？先4人小组讨论一下，再动手画一画。

生：

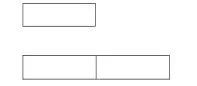
师：数学家们经常用线段图来表示数量之间的关系。（边讲边出示线段图）用这一条线段表示一份数，2段这么长的线段就表示它的2倍。

思考：

首先通过摆一摆、拍一拍等活动，让学生逐渐从感性认识开始向理性理解过渡，进一步巩固倍的认识。

接着让学生创造2倍关系图，再从中抽象、概括，用一个图表示所有的2倍关系，逐步逼近线段图。在多样的情境中，不同形态的非本质属性方面的变化，需要孩子去捕捉其中不变的本质因素。在这样的思维活动体验中，获得的概念就更精确、更稳定。

二、运用数形结合分析数量关系

解决问题的关键是帮助学生理解和分析数量关系，采用数形结合的方法，把抽象的数量关系正确、直观地表现出来，可以更好地吸引学生的注意力，同时可以培养学生的观察能力，增强学生思维的深刻性，从而提高学生的解题能力。

案例2：《连乘问题》教学片断

1.课件出示教材第52页例3超市销售保温壶情境图。

2.提问：你们从刚才的图片中收集到了哪些数学信息？数学问题是什么？同桌交流，指名汇报。

3.要求：一共卖了多少钱？你会先求什么，再求什么？

小组合作交流：

①拿出课前准备好的纸盒和保温壶图片，摆一摆，看一看，说一说。②尝试画线段图分析数量关系。

思考：1.通过小组合作交流，借助保温壶、纸箱等实物图片，帮助学生直观理解，让学生的思维变成看得见、摸得着的东西。

2.尝试画线段图分析理解，既体现了教法与学法的多样性，又体现了数形结合的模式。线段图能形象、直观地反映应用题的数量关系，是应用题中实际事物数量方面的“表象”，它能起到化隐为显，使数量关系明朗化的作用，有利于寻求解题思路，它是直观与抽象的对立统一体。

三、运用数形结合拓展思维能力

数学是锻炼思维的体操，数学的教学目的就是要培养数学思维能力，在小学主要培养学生初步的逻辑思维、形象思维和直觉思维能力。数形结合的思想能够变抽象思维为形象思维，有助于把握数学问题的本质。

案例3：《数与形》教学片断（1）

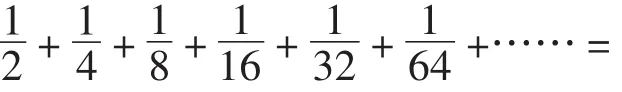
师：观察这个算式，它有什么特点？

师：算式最后的省略号是什么意思？

生：后面还有很多数，有无数个。

师：无数个就是数也数不完，按照这样的规律无尽地加下去，结果会等于多少呢？（让同学们猜一猜）

师：没感觉是吗？不着急，我们刚刚说了，数可以帮形，其实形也可以助数。同学们，你们可以利用图形帮助自己找找感觉。

请学生拿出练习纸（提示：把自己拿到的图形看作单位“1”）

师：请你用你练习纸上的图形来帮助自己，看看能不能找到和是多少。四人一小组展开讨论。要求学生一定要涂一涂，画一画，组长操作，其他同学参考。

交流：出示三种不同的图形作品，让学生感受最后的结果。（结合算式讲解）

1.圆形 2.正方形 3.线段

让孩子介绍，自己画的过程，让学生感受最后的结果。

师：听完了他们的介绍，你认为按这样的规律加下去，算式的结果会是多少呢？

生：有的孩子可能认为等于1，有的孩子可能认为无限接近1。

师：虽然同学们得出的结果不相同，但是我看出结果也有共同的地方，都和谁有关？

生：都和1有关系。

师：无论是觉得等于1，还是觉得和1差一点，起码我们有了一个方向。是谁帮助我们找到了方向呢？

生：图形。

师：对，这就是图形的好处，它能给我们感觉，让我们找到接近结果的方向。但是我们还有困惑，结果到底是怎样的呢？你们觉得图能回答这个问题吗？

生：不能。

师：这就是图的缺陷，它不能准确、精细地表示结果。但是我们可以借助数来对它进行验证，请同学们看一看。出示逆向思考的过程。

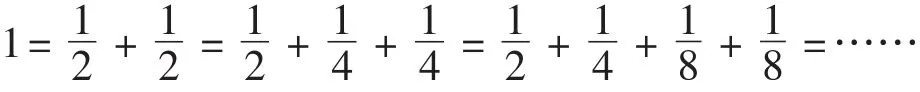
通过上面的题目，你觉得数和形有关系吗？

师：是的，数与形的关系密切，你来帮我，我来助你。

《数与形》教学片断（2）

为什么a×b+a×c=a×（b+c）？请画图解释。

思考：

数与形的例题及乘法分配律的反运用都是学生认知上的一个障碍，有时很难用语言来描述，如果结合图形来帮助学生理解，通过图形变“无形”为“有形”，借助图形完成转化，对学生来说，收获的不仅仅是知识方法，还经历了一次发现、体验和创造的过程，对数和形的结合会有更深刻的体会和感悟。

四、运用数形结合提高解题能力

数形结合思想是一种可使复杂问题简单化、抽象问题具体化的数学思想方法。巧妙运用数形结合的思想方法解决一些抽象的数学问题，可起到事半功倍的效果。

例如：甲、乙两车都从A地到B地，甲车比乙车提前30分钟出发，行到全程时，甲车发生了故障，修车花了15分钟，结果比乙车晚到B地15千米，甲车修车前后速度不变，全程为300千米，那么，乙车追上甲车时距A地多少千米？

思考：行程应用题对于小学生来说本身就是一个难点，信息一多更是不知从何下手，用方程来解答也有一定难度。可如果用数形结合的方法来解答就容易多了，画图如下：

从图中我们不难发现，乙车追上甲车时距A地300÷2＝150（千米），因为甲车提前了15分钟（提前30分钟减去修车的15分钟），又晚到15分钟，根据图形的对称性，就知乙车在中点追上甲车，这样问题就迎刃而解了。

总之，看“形”思“数”，见“数”想“形”，通过数形结合，实现转化，不仅能丰富分析和解决问题的策略，更有助于透彻地理解数学关系的本质，提升学生的数学素养。

程小爱（1968—），男，江西永修人，永修县新城小学，高级教师，研究方向为小学数学教学。

责任编辑徐艳兰