培养学生数学核心素养的研究与实践

方兆继

（广德县教学研究室，安徽宣城 242200）

培养学生数学核心素养的研究与实践

方兆继

（广德县教学研究室，安徽宣城 242200）

数学思想方法是在启发学生数学思考的过程中逐步积累和形成的，它不是一朝一夕就能立竿见影，必定要经历一个循环反复、螺旋上升的过程。因此在教学中，教师要重视数学思想的教学，根据学生认知规律、年龄特征，挖掘蕴含在教材显隐性资源，创造并把握运用数学思想解决问题的机会，主动培养学生运用数学思想的意识，使学生从数学思想方法的高度把握知识的本质和内在规律，逐步体会数学思想方法的精神实质，从而使数学素养全面提高。

数学素养；课堂教学；数学本质

核心素养是学生数学素养的重要标志。数学素养是通过数学的学习建立起来的一些思想、方法，以及用数学的思想方法处理和解决问题的能力。数学核心素养是基于认数、计算、测量、统计等具体的数学知识与技能而形成的思想与方法，以及对数学在现实社会与生活中的作用与价值的认识。

一、深入挖掘教材，培养数学核心素养

数学核心素养一般与学习领域内容相关。如，数感、符号意识、运算能力与“数与代数”领域直接相关，在学习数的认识、数的运算、运用字母表示数等内容时，与这些核心素养直接联系，数的认识学习过程有利于形成学生的数感，建立数感有助于学生数的理解和把握。数学知识在内容上贯穿两条主线，一是数学基础知识，是一条“明线”，它直接以文字形式写在教材里；二是数学思想，是一条“暗线”，隐藏在基础知识的背后，是无“形”的，需要教师通过对教材加以分析挖掘，拨云去雾，才能显露出来。新教材注重贯彻四基目标，低年级教材知识看似简单，但也蕴含了丰富的数学思想，各种思想联系紧密，互相渗透，一个数学内容往往是几种思想方法交织在一起。

以一年级上册“比多少”教材为例：

图1 情境图

图2 比多少

教材中小猴和各类水果是散乱放在一起的，教学时要先进行分类（分类思想）；统计出数量（统计思想），再根据数量多少来比较数的大小（一一对应思想），并引出符号＞、＜、=（符号思想）。简单的一课中蕴含着丰富的隐性数学思想，这就需要教师挖掘提炼，有意识地从教学目标的确定、教学过程的预设、教学效果的落实等方面来渗透数学思想，从而发展学生数学素养。

抽象思想是重要的数学基本思想之一，存在于数学学习的全过程。低年级教材主要是让学生能从具体情境中抽象出数量和变化规律，并用符号表示，符号化的过程就是一个抽象的过程。从情境图抽象出数字符号0～9，关系符号=、＜ ＞，运算符号+ 、－、×、÷都是典型的符号化。在数的教学中，可根据教学的实际情况，适当地展示数字的形成过程和所运用的思想，让学生体验符号思想的简明，培养学生的创造性思维。

二、注重过程，培养学生核心素养

为了更好地培养学生的数学思维品质，教师不仅要对教材进行研究，潜心挖掘，还要讲究数学思想渗透的手段和方法，回归和再现知识的形成过程，让学生在探究过程中自主发现潜藏其中的思想方法，体验数学思想魅力，从而提高数学素养，这才是数学教学应有的视界。

小学数学中有相当的比重是计算，教学中要引导学生在观察、比较、抽象、概括中理解算理，掌握方法。数形结合是理解算理的很好的方式。如一年级下册“两位数加一位数和整十数”，教学25+2和25+20时，教师先请学生摆小棒，在对比中学生明白：2要和25中的5相加，它们的计数单位都是1；20要和25中十位上的2相加，它们的计数单位都是十。这样，通过摆小棒，有效渗透数形结合思想，使复杂问题简单化，抽象问题具体化，相同数位相加的算理简明直观，学生在理解算理的基础上掌握计算方法，发展数学思维。

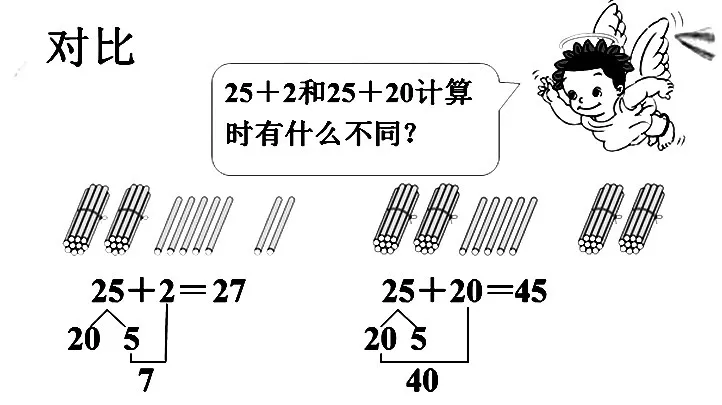
图3 两位数加一位数、整十数

又如在量的教学中，首要问题是要合理引入计量单位。在“面积与面积单位”的教学中，教师可以这样设计：当观察、重叠都无法直接比较两个图形面积的大小时，引入小方块，并把它一个个铺在两个图形上，这样，使两个图形的面积得到量化，使形的问题转化为数的问题；接着又出示大小不一的方块进行测量，得到与观察结果不符的数，进而使学生意识到，任何量的量化都必须有一个统一的标准，这样自然引入计量单位。

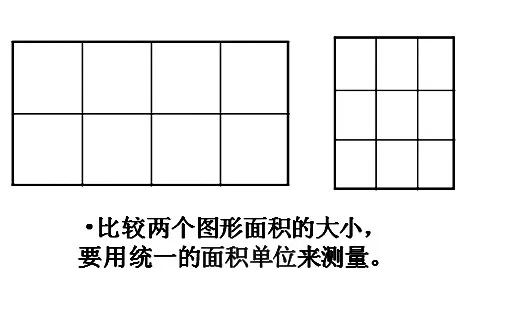
图4 用小正方形进行测量

图5 小正方形大小要有统一标准

数学在本质上就是在不断的抽象、概括、模式化的过程中发展和丰富起来的。数学学习只有深入到模型的意义上，才是一种真正的数学学习。低年级学生以形象直观思维为主，需要由具体、形象的实例开始，借助操作予以内化和强化，最后通过思维发散和联想加以扩展和推广。

数学思想方法渗透是无形的，是无法传授的，只有让学生一次次经历、体验后才能感悟。教学中要有意识地引导学生经历知识的形成过程，让学生在自主探究时、在合作交流中不仅学到数学知识，还发现知识背后蕴含的数学思想，得到积极的情感体验，培养学生核心素养。

三、学以致用，培养学生核心素养

数学思想方法的教学，不仅是为了指导学生有效应用知识，更是培养学生的思维品质。教学中要加强学生的应用意识，鼓励学生运用已学的数学思想方法去发现、分析问题，引导学生加以抽象、概括，建立数学模型，探求解决问题的一般方法，培养学生自觉的应用意识，进而积累数学思想，培养学生核心素养。

如：在教学三年级《数学广角——排列组合》一课中，在解决“2件上装和3件下装一共有几种不同的搭配方法？”时，借助图形连线，学生观察到：下装有3件时，一件上衣就有3种搭配，2件上衣就有2×3种搭配方案；下装是4件时，2件上衣就有2×4种搭配方案。

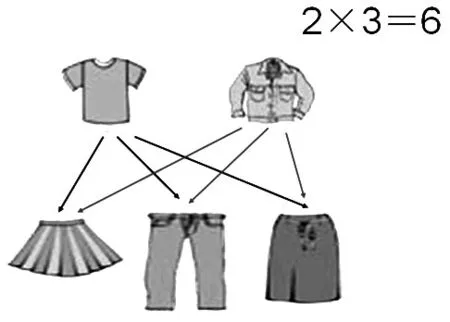
图6

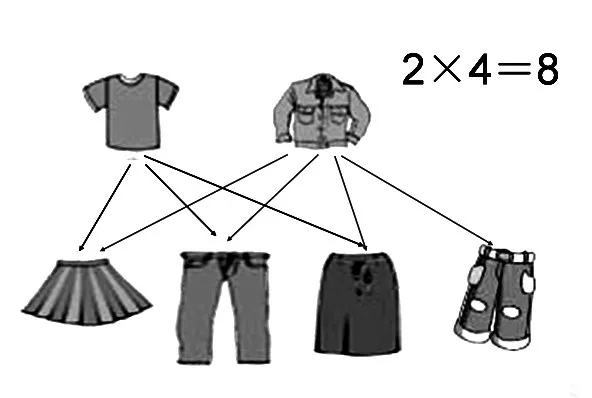
图7

这样由具体、形象的实例开始，借助操作予以抽象概括，通过形—数—算的数学思想的层层递进，建立模型，学生就可以脱离实物图举一反三，通过思维发散和联想加以扩展和推广，解决早餐问题、路线问题，渗透数学建模思想，学生的数学素养得到提升。

教材编写中将一些重要的数学概念与数学思想方法的内容，采用螺旋上升的方式。教师在使用时，要加深对教材的理解和挖掘，采用逐步深化的方式，潜移默化地融数学思想方法于知识教学、技能培养之中，以便逐步实现每一个阶段的渗透目标，同时还要注意各种思想方法间的承接关系，做到每个阶段都有所提升、有所拓展，切实提高学生的数学素养。

这样，抓住知识间的联系，借助于直观图示的形象支撑，让学生充分展开探索过程，建立起一位小数的“直观模型”。接着借助长度单位这个背景，让学生自主拓展到百分之几的分数用两位小数表示，实现知识的正迁移，这种形象的直观模型对后面学习三位小数以及抽象概括小数的意义无疑具有统摄作用。在渗透思想方法的时候，教师引导学生自觉地运用学到的思想方法去迁移拓展，提高学生自觉的应用意识，积累数学思想。

数学思想方法是在启发学生数学思考的过程中逐步积累和形成的，它不是一朝一夕就能立竿见影，必定要经历一个循环反复、螺旋上升的过程。因此在教学中，教师要重视数学思想的教学，根据学生认知规律、年龄特征，挖掘蕴含在教材中的隐性资源，创造并把握运用数学思想解决问题的机会，主动培养学生运用数学思想的意识，使学生从数学思想方法的高度把握知识的本质和内在规律，逐步体会数学思想方法的精神实质，从而使数学素养全面提高。

方兆继（1977—），男，安徽广德人，广德县教学研究室，小学高级教师，研究方向为小学数学教学。

责任编辑徐艳兰