电热式变温液体黏度测量装置的设计与应用

王林菲,张春影,王 丹,季刘方,王 军

(中国石油大学(华东) a.储运与建筑工程学院; b.理学院，山东 青岛 266580)

电热式变温液体黏度测量装置的设计与应用

王林菲a,张春影a,王 丹a,季刘方b,王 军b

(中国石油大学(华东)a.储运与建筑工程学院;b.理学院，山东 青岛 266580)

设计了基于“落球法”的电热式变温液体黏度测量装置. 借助该装置，通过改变2个侧加热板的间距，在室温下研究了侧加热板以及容器壁对蓖麻油中小球下落速度的影响，并以此为基础，利用对称测量原理，对蓖麻油在不同温度下的黏度进行了测量，揭示出蓖麻油的黏度与温度的关系近似满足阿伦尼乌斯公式，活化能约为9.213×10-20J.

黏度；落球法；温度；蓖麻油

液体的黏度与温度有关[1]，准确测量液体的黏度并掌握其对温度的依赖关系具有重要价值[2-4]. 在液体黏度的常用测量方法中[5-8]，落球法由于所需装置简单，物理思想清晰，因而在大学物理实验教学中被普遍采用[9]. 基于落球法，本文提出了电热式变温液体黏度测量装置，其与水浴式变温液体黏度测量仪相比[10-13]，不仅可以通过改变侧加热板的间距，研究侧加热板和容器壁对小球的终极速度的影响，而且可以使待测液体快速加热并基本稳定于所需温度，从而实现待测液体在不同温度下的黏度测量.

1 测量装置与实验原理

电热式变温液体黏度测量装置如图1所示，由待测液体、盛装液体的长方体容器(简称容器)、2块可相对移动的侧加热板、1块固定的底加热板以及高精度数字控温仪等组成. 容器采用透明的有机玻璃板粘接而成，内部尺寸为16.00cm×4.00cm×25.00cm. 加热板由薄铝板夹持硅胶加热片构成，底加热板固定于容器内的底部，而2个侧加热板则通过水平支撑梁悬挂于容器内. 各加热板与数字控温仪之间通过导线连接，数字控温仪的探头位于由计时起点和计时终点标志线所确定的测量区间中部，并贴近于容器的内壁固定. 由计时起点和计时终点标志线所确定的测量区间处于容器的中下部，这样的设置可以保证在不同的温度条件下小球在测量区间的下落都是匀速的.

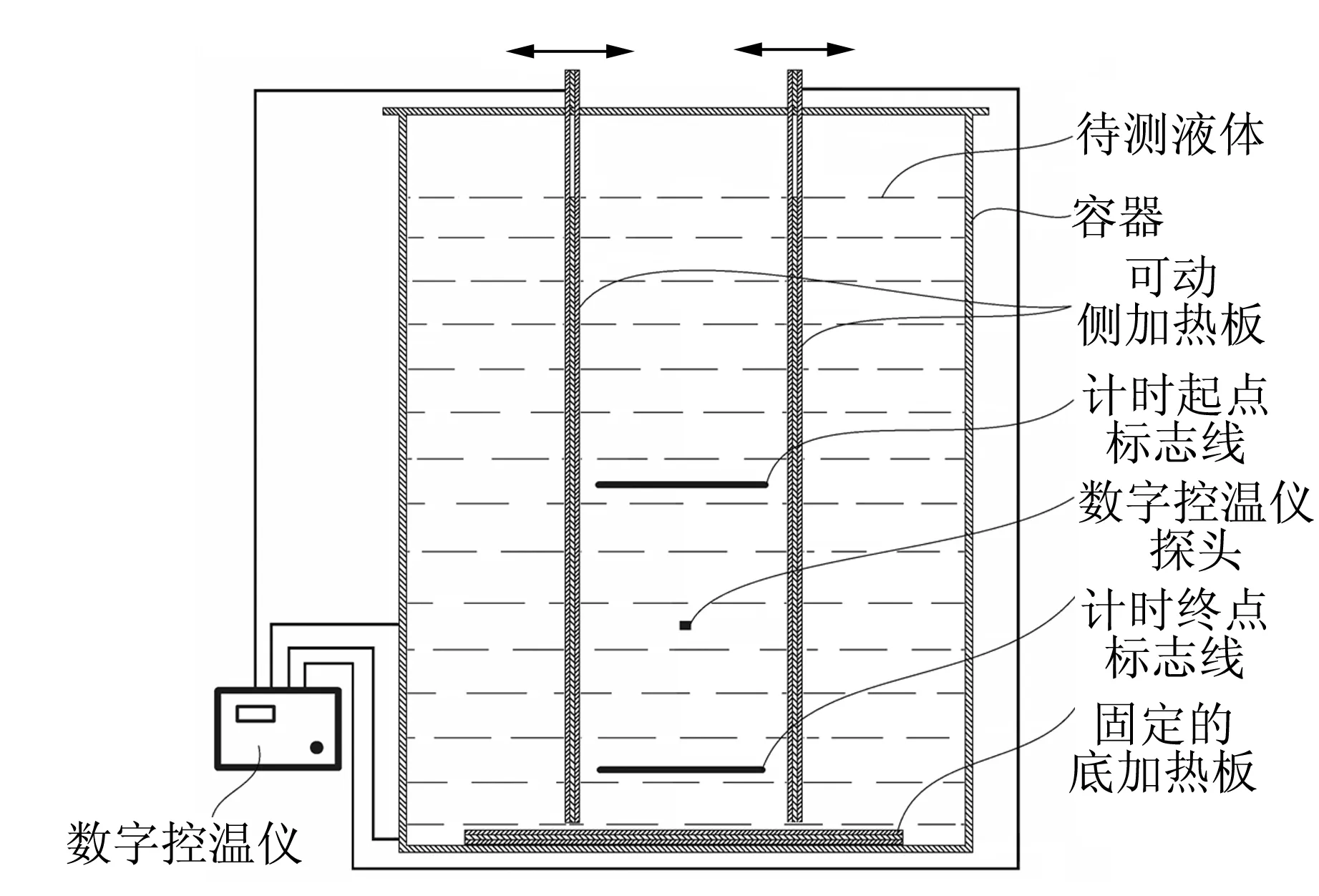
图1 测量装置结构示意图

为了获得液体在不同温度下的黏度，测量装置在设计和使用上做了以下2点考虑：首先，容器采用了4.0mm厚的有机玻璃板粘接而成，其作为一道有效的隔热屏障，再配合较大的容积，对蓖麻油、橄榄油、甘油、变压器油、机油等导热系数相对较小[0.13～0.28W/(m·K)]的液体进行测量，可以较好地避免因与周围环境存在热交换而引起的液体温度剧烈变化，以31.0 ℃的蓖麻油为例，当环境温度为18.0 ℃时，其温度下降1.0 ℃约需8min，这样的下降速度足以使实验者有机会选择某个温度，并实现对该温度下蓖麻油黏度的有效测量；其次，测量装置中设置了2块侧加热板和1块底加热板，并用水作为参照，通过优化底加热板的功率以及侧加热板的散热面积，减小了液体对流对垂直方向上温度分布的影响. 实际观测表明：水在计时起点和计时终点处中心轴线上的温度差异小于0.5 ℃，但对于其他液体而言，由于热容与导热系数发生变化，计时起点和计时终点处中心轴线上的温度差异可能会有所增加. 此时，可以采用对称测量法，亦即以测量区间中点处的温度Tc为基准，用小球通过测量区间的平均速度代替小球在温度为Tc的液体中匀速下降的速度，从而近似地得到与Tc温度相对应的液体黏度.

实验过程中，让小球在温度为T(摄氏温标)的待测液体中沿容器的中轴线下落，当其匀速通过测量区间时，小球受到的浮力、重力和黏滞力达到平衡，根据斯托克斯定律，液体的黏度η可表示为[9]

(1)

式中，m,V,D和v分别为小球的质量、体积、直径和下落速度(即终极速度)，ρ为与温度T相关的液体密度，g为重力加速度. 由于斯托克斯定律仅适用于无限广延的静止液体，因此式(1)中的终极速度还应修正为

(2)

式中，v′为无限广延条件下的小球终极速度，d为2块侧加热板的间距，b=4.00 cm为容器的内部厚度，h=10.00 cm为测量区间的高度，k1和k2为待定的修正系数，它们与实验条件相关[14]. 由于r≪h，故式(2)又可简化为

(3)

即

(4)

显然，只要不断改变2块侧加热板的间距，并同时测量出小球在该条件下通过测量区间的速度，就可以借助作图法得到所需的修正系数k1.

此外，斯托克斯定律是根据理想状态下(无涡流)的流体普遍运动方程得出的，因此，在具体应用时还需引入雷诺数来评价是否存在涡流. 雷诺数R的具体形式为[9]

(5)

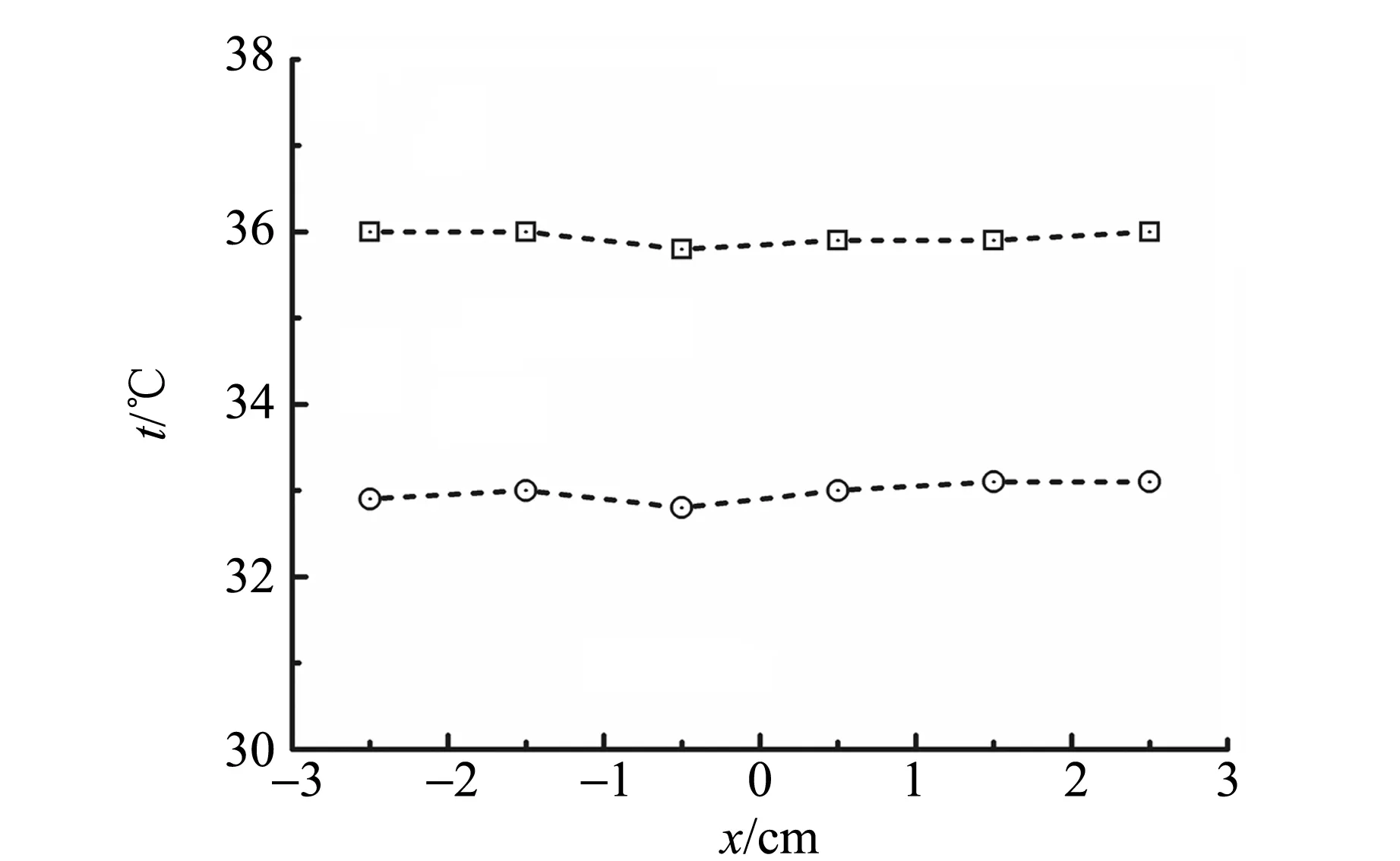
如果R<0.1，可以认为不存在涡流，液体的黏度可由式(1)和式(3)直接给出；如果0.1

(6)

不同的液体由于性质不同，其黏度对温度的依赖性也不同. 假如待测液体是一种无定形的黏性流体(如蓖麻油等)，则它的黏度与温度的关系可近似地表示为[15]：

(7)

式(7)称为阿仑尼乌斯公式，其中，A为与温度无关但与液体性质有关的系数，k为波尔兹曼常量，Ta=t+273.15为液体的热力学温度，w为液体的活化能. 对式(7)进一步处理可得：

(8)

由此可知ln (η/Ta)与1/Ta应呈线性关系. 通过实验测量出不同温度下液体的黏度，并绘制ln (η/Ta)与1/Ta的关系曲线，如果关系曲线具有足够的线性度，则表明所研究的液体是无定形黏性流体，其黏度可用式(7)进行描述.

2 实验结果与讨论

利用图1所示装置进行实验，实验中采用平均直径为2.009 mm、平均质量为0.032 7 g的金属小球，配合冰箱、数字秒表等对蓖麻油在不同温度下的黏度进行测量. 作为上述工作的前提和基础，实验过程中不仅在室温(t=27.0 ℃)条件下考察了侧加热板间距d对小球终极速度v的影响，通过分析1/v对1/d的依赖关系，得到了修正系数k1，而且还考察了测量区间内水平和垂直方向上蓖麻油的温度分布，为测量蓖麻油在不同温度下的黏度提供了依据.

图2(a)给出了不同的侧加热板间距d所对应的小球终极速度v，根据拟合曲线可知，随着侧加热板间距d的增加，小球的终极速度v近似地呈指数形式增加，说明侧加热板以及容器壁对小球的下落过程存在显著影响. 为了确定式(3)和式(4)中的修正系k1，又进一步分析了1/v随1/d的变化情况，结果如图2(b)所示，很明显，1/v与1/d线性相关，这与式(4)的预期一致. 使用Origin软件进行线性拟合，并将拟合结果与式(4)进行比较，可以得到k1=2.68，其与文献[9]和[16]中给出的k1=2.4相比存在一定差异，这说明修正系数k1确实与实验条件有关[14]. 将所得到的k1以及相关数据代入式(3)，即可得到无限广延条件下小球终极速度v′的计算公式.

(a)v对d的依赖关系

(b)v-1对d-1的依赖关系图2 侧加热板间距d对27.0 ℃的蓖麻油中小球终极速度的影响

当d=8.00 cm时，测量得到的小球通过测量区间的终极速度v=2.540 cm/s，修正后的终极速度v′=2.802 cm/s，利用上述结果以及相关公式可以计算出蓖麻油在室温(即27.0 ℃)下的黏度η=0.530 Pa·s，与文献[16]给出的该温度下的蓖麻油黏度标准值η′= 0.53 Pa·s完全相同，由此可知，利用图1所示装置可以对液体在室温下的黏度进行精确测量.

当d=8.00 cm时，以测量区间中点为基准，测量了不同温度下蓖麻油在水平和垂直方向上的温度分布，结果如图3所示. 从图3(a)可以看出，蓖麻油在水平方向上的温度分布比较均匀，这说明即使小球偏离中心轴线下落，可信的测量也可实现. 与水平方向上的温度分布相比，在垂直方向上的温度分布均匀性略差[见图3(b)]，统计分析表明，对于所选定的测量区间，其上下两端面中心的温度差异约为1.0 ℃，由于温度差异比较小，因此能够采用对称测量法，以测量区间中点处观测到的温度为基准，近似地研究蓖麻油在不同温度下的黏度，并揭示其随温度的演变规律.

(a)水平方向

(b)垂直方向图3 蓖麻油的温度分布

控制侧加热板间距d为 8.00 cm，借助冷藏和随后的电加热，在室温附近测量了不同温度下蓖麻油的黏度η，并与文献[16]给出的标准值η′进行了比较，相关数据如表1所示. 从表1给出的结果可以看出，随着温度的升高，蓖麻油的黏度迅速减小.

为了揭示蓖麻油的黏度与温度之间的依赖关系，进一步分析了ln (η/Ta)随1/Ta的演变规律，结果如图4所示，从图中可以看出，ln (η/Ta)与1/Ta近似线性相关，使用Origin软件进行拟合后可以得到：

校正的决定系数R2=0.983 22接近于1，表明ln (η/Ta)与1/Ta之间具有线性关系，亦即蓖麻油的黏度对温度的依赖性可以采用阿仑尼乌斯公式描述，具体形式为

将上式与式(7)进行比较可以得出蓖麻油的活化能约为9.213×10-20J，其与文献[17]给出的蓖麻油活化能9.961×10-20J相比，相对偏差约为7.5%.

表1 不同温度下蓖麻油的黏度

注：η′取自文献[16].

图4 ln (η/Ta)与Ta的关系曲线

3 结束语

与水浴式变温液体黏度测量仪相比，所设计的电热式变温液体黏度测量装置具有结构简单、成本低廉、操作方便等特点，此外，该装置还吸收了多管式液体黏度测量仪的优点，能够用来研究侧加热板以及容器壁对小球下落速度的影响，进而获得小球在无限广延液体中的终极速度. 利用该装置对室温以及其他温度下的蓖麻油黏度进行了测量，测量结果不仅表明了该装置在设计思想上的合理性，而且也证明了蓖麻油的黏度与温度的关系近似地符合阿伦尼乌斯定律.

[1] 倪玲英. 工程流体力学[M]. 东营:中国石油大学出版社,2012.

[2] 易玉峰,李术元,丁福臣. 石油粘度关联预测模型研究进展[J]. 当代化工,2008,37(5):532-536.

[3] 吕建强,韩仲岩. 血粘度24小时周期节律性变化与缺血性中风的发病关系[J]. 中国神经精神疾病杂志,1991(1):58-60.

[4] 钱祖文. 颗粒介质中的粘滞系数[J]. 物理学报,2012,61(13):220-223.

[5] 王玉清,任新成. 落球法测液体粘度实验的改进[J]. 大学物理,2004,23(8):41-42.

[6] 刘振东,吴洁. 转筒法液体黏滞系数公式的研究[J]. 计量技术,2009(2):27-29.

[7] 陈刚,朱震刚. 利用强迫振动扭摆方法测量液体粘滞系数的原理[J]. 物理学报,1999,48(3):421-425.

[8] 饶黄云,刘悦. 用自制仪器精确测定变温液体的粘滞系数[J]. 实验力学,2008,23(2):186-192.

[9] 李书光. 大学物理实验[M]. 北京:科学出版社,2012.

[10] 王美亭,刘中山. 蓖麻油的粘滞系数与温度关系曲线拟合[J]. 河南师范大学学报(自然科学版),1992,20(3):108-111.

[11] 陆申龙,金浩明,曹正东. 液体粘滞系数与温度关系实验及曲线拟合[J]. 物理实验,1988,8(3):122-124,133.

[12] 武瑞兰,田静. 蓖麻油粘滞系数随温度变化的经验方程[J]. 山东工业大学学报,1998,28(1):94-96.

[13] 陈洪叶,赵文丽,李国栋. 用单管落球法探讨蓖麻油粘度随温度的变化[J]. 大学物理实验,2007,20(1):47-50.

[14] 高德文,赵英. 落球法测量液体粘滞系数的实验研究[J]. 北京石油化工学院学报,2016,24(1):64-66.

[15] Ojovan M I, Travis K P, Hand R J. Thermodynamic parameters of bonds in glassy materials from viscosity- temperature relationships [J]. Journal of Physics Condensed Matter,2007,19(41):415107.

[16] 沙振舜,周进,周非. 当代物理实验手册[M]. 南京：南京大学出版社,2012.

[17] 张欢,马全喜. 黏滞法估算液体的活化能[J]. 物理通报,2009(5):14-16.

Developmentandapplicationofelectric-heatedtemperature-variablemeasuringdevicefortheviscosityofliquid

WANG Lin-feia, ZHANG Chun-yinga, WANG Dana, JI Liu-fangb, WANG Junb

(a. College of Pipeline and Civil Engineering; b. College of Science, China University of Petroleum, Qingdao 266580, China)

Based on the falling ball method, the electric-heated measuring device for the viscosity of liquid at different temperatures was proposed and developed. The effects of the side heating plates and the container walls on the dropping velocity of the ball in castor oil at room temperature were investigated by changing the distance between two side heating plates. The viscosities of castor oil at different temperatures were measured according to the symmetric principle. The experimental results not only justified the design of the device, but also revealed that the temperature dependence of the viscosity of castor oil approximately obeyed the Arrhenius law, and the activation energy of castor oil was about 9.213×10-20J.

viscosity; falling ball method; temperature; castor oil

O4-33

A

1005-4642(2017)10-0049-04

[责任编辑：郭 伟]

2017-04-21

王林菲(1995-)，女，山东淄博人，中国石油大学(华东)储运与建筑工程学院2014级本科生.

指导教师：王 军(1969-)，男，山东淄博人，中国石油大学(华东)理学院高级实验师，博士，主要研究方向为离子注入和材料改性以及物理实验技术.