基于改进拟动力法的主动土压力分析研究
张 磊 ,孙树林 ,2,储 浩 ,丁 伟
基于改进拟动力法的主动土压力分析研究
张 磊1,孙树林1,2,储 浩1,丁 伟1
(1.河海大学 地球科学与工程学院,江苏 南京 210098;2.河海大学 水文水资源与水利工程科学国家重点实验室,江苏 南京 210098)
地震条件下土压力的获取在目前的研究中通常采用拟动力方法,此方法往往忽略了后填土介质的粘弹特性及自由表面零应力这个边界条件。为了弥补现有拟动力方法的不足,考虑地震波传播介质的粘弹特性,改进原有的拟动力法;进而推求含有超载角的倾斜挡墙的主动土压力及其临界破坏时的破裂角计算公式,分析了超载角、地震力系数等参数对临界破裂角及主动土压力系数的影响。结果表明:临界破裂角随竖直地震力系数的增大而增大;水平地震力系数、超载角、内摩擦角以及挡土墙倾角对挡土墙设计影响大。
地震;挡土墙;主动土压力;临界破裂角;改进拟动力法
挡土墙作为一种常见的支挡结构,可以有效地防止墙后岩土体失稳破坏,被广泛地应用于建筑、水利、交通等工程中[1]。因此,挡土墙土压力的计算一直是工程界的一大课题,特别是地震条件下动土压力计算问题,国内外学者专家均做过大量的研究[2-5]。目前,挡土墙地震土压力的计算方法主要有Mononobe-Okabe,它属于拟静力方法的范畴。拟静力方法是将地震荷载简化为恒定荷载,忽略了地震波传播中的相位差以及时间对地震荷载的影响作用,这显然与实际不相一致。为了弥补此方法的缺陷,文献[6-7]等采用拟动力法,引入地震力,考虑地震力随时间的变化,形成了一种新的土压力计算方法。之后,许多学者在此研究思路的基础上进行了改进和扩展[8-9]。然而现有的拟动力法在运用到挡土墙后填土的分析之中时,具有一定的局限性[10-11],它违背了自由表面零应力的这个边界条件。
为了弥补传统拟动力法的不足,考虑地震波传播介质的粘弹特性,改进现有方法。在此基础上,进而推求倾斜挡土墙后填土在地震作用下主动土压力以及挡土墙后填土的临界破裂角的计算公式,并研究了其随着各类参数变化的变化情况,讨论了影响主动土压力系数和临界破裂角大小变化的主要参数。
1 改进拟动力法的基本方程
基于材料的性质,Kelvin-Voigt粘弹性介质中水平ah(z,t)和竖直的地震加速度av(z,t)为[12]:
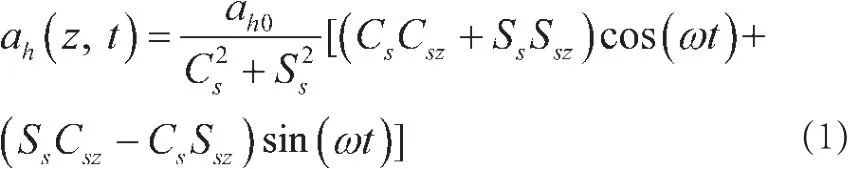
其中:
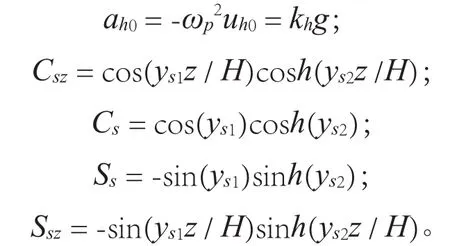
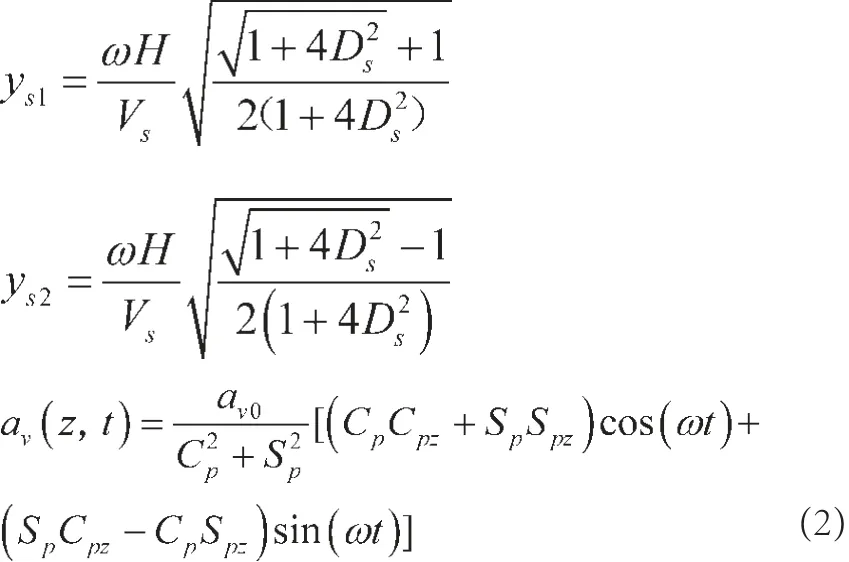
其中:
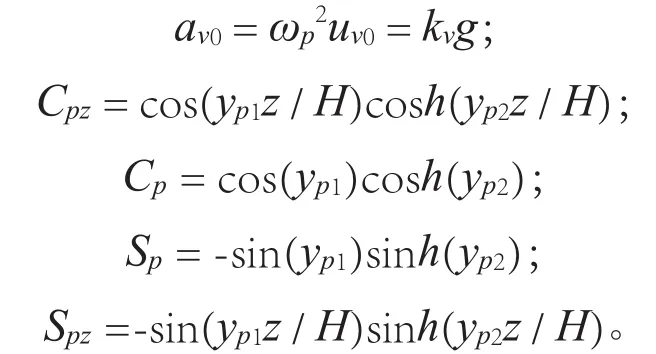

式中:ω为运动角频率;t为时间;Ds、Dv为填土的阻尼比;Vp、Vs分别为横波以及剪切波波速;H为挡土墙高度;z为填土顶部往下的深度;g为重力加速度,ys1、ys2、yp1、yp2为无量纲常数。
2 计算模型建立
现存的改进拟动力法只考虑了填土面为水平时的地震力,具有局限性。本文建立了倾斜填土的地震力计算模型。为了粘弹性波的传播,以及计算的需要做出以下假设[13]:填土体材料均被假设为干燥的Kelvin-Voigt材料;挡土墙为刚性的;填土的剪切模量保持不变。
挡土墙后填土受力情况如图1所示。图中墙高H,墙背面与竖直方向的夹角为θ,墙背摩擦角为σ,墙后填土的内摩擦角为φ,填土的超载角为β,重度为γ,填土的重力为W,地震力为Q,主动土压力为Ρae。
3 地震作用下主动土压力计算公式推导
如图1所示,对填土破坏体进行条分,则倾斜薄层单元的质量可以表示为

图1 填土体的模型及受力情况Fig.1 The model of filling soil and its stress

则水平方向的地震力可表示为如下:

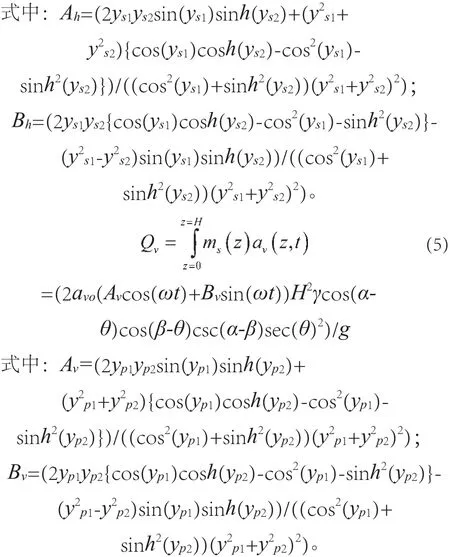
通过力的平衡关系可得:
(3)设计/开发解决方案:能够针对复杂的非数值处理问题设计合理的解决方案,并能够在设计环节中体现创新意识,从而具备计算机软件工作所需要的基本能力。
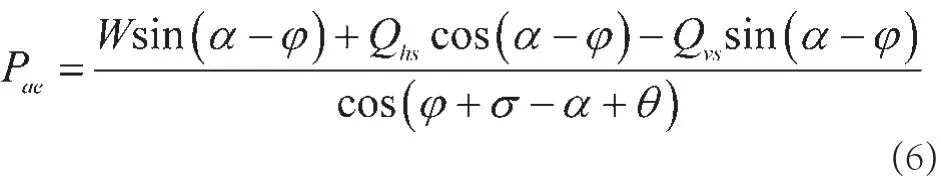
主动土压力系数可表示为
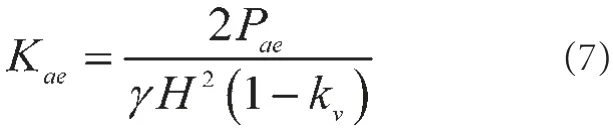
4 临界破裂角的求解
由上述分析可知,填土的主动土压力为Ραe,由可计算出填土的临界破裂角[14]。通过计算和化简可得临界破裂角的公式如下:


式中:q1= Qhcos(θ+σ+φ) +(W - Qv)sin(θ+σ+φ);

5 算例分析
为了进行本文的参数研究,各参数取值如下:挡土墙后填土的重度γ=18 kN/m3;地震波的周期T=0.3 s;挡土墙高度H=10 m;在填土中剪切波以及主波的速度分别为Vs=100 m/s,Vp=1 500 m/s;剪切波和主波的阻尼比分别为Ds=10%,Dp=5%。利用MATLAB软件,求解下列问题。
5.1 临界破裂角
求解t/T在0~1之间变化时,所求的α的最小值,即为临界破裂角的值。

表1 地震力系数对临界破裂角的影响Tab.1 Effect of seismic force coeff cient on critical rupture angle
5.1.1 地震力系数对临界破裂角的影响
取挡土墙后填土内摩擦角φ=30°,挡土墙与后填土之间的摩擦角δ=15°,挡土墙倾角θ=5°,填土超载角β=0°。当kh=0.1、0.15、0.2,kv=-0.1、0、0.1时,计算结果如表1所示。从表1中可以看出,随着kv的增大,α也随着增大;随着kh的增大,α在逐渐减小。其中,kv对破裂角的影响较小,而随着kh的增大,kv对破裂角的影响逐渐增大。Kh对破裂角影响较大,最大的单位减小幅度为16.5%。
取地震力系数kh=0.1,kv/kh=0.5,超载角β=0,挡土墙倾角θ=5°时,挡土墙后填土内摩擦角φ=20°、30°、40°,挡土墙与后填土之间的摩擦角δ=0°、φ/4、φ/2、3φ/4、φ,临界破裂角随填土内摩擦角及挡土墙与填土间内摩擦角的变化如表2所示。从表2中可以看出,随着挡土墙后填土内摩擦角φ的增大,α也随着增大。随着挡土墙与后填土之间的摩擦角δ的增大,α随着减小。当φ越小,挡土墙与后填土之间的摩擦角δ对临界破裂角α的影响越大。
5.1.3 挡土墙倾角对临界破裂角的影响
取挡土墙后填土内摩擦角φ=30°,挡土墙与后填土之间的摩擦角δ=15°,超载角β=0,挡土墙倾角从0°变化到15°,临界破裂角随挡土墙倾角变化线如图2。从图2中可以看出,随着挡土墙倾角θ的增大,临界破裂角α也随之增大。
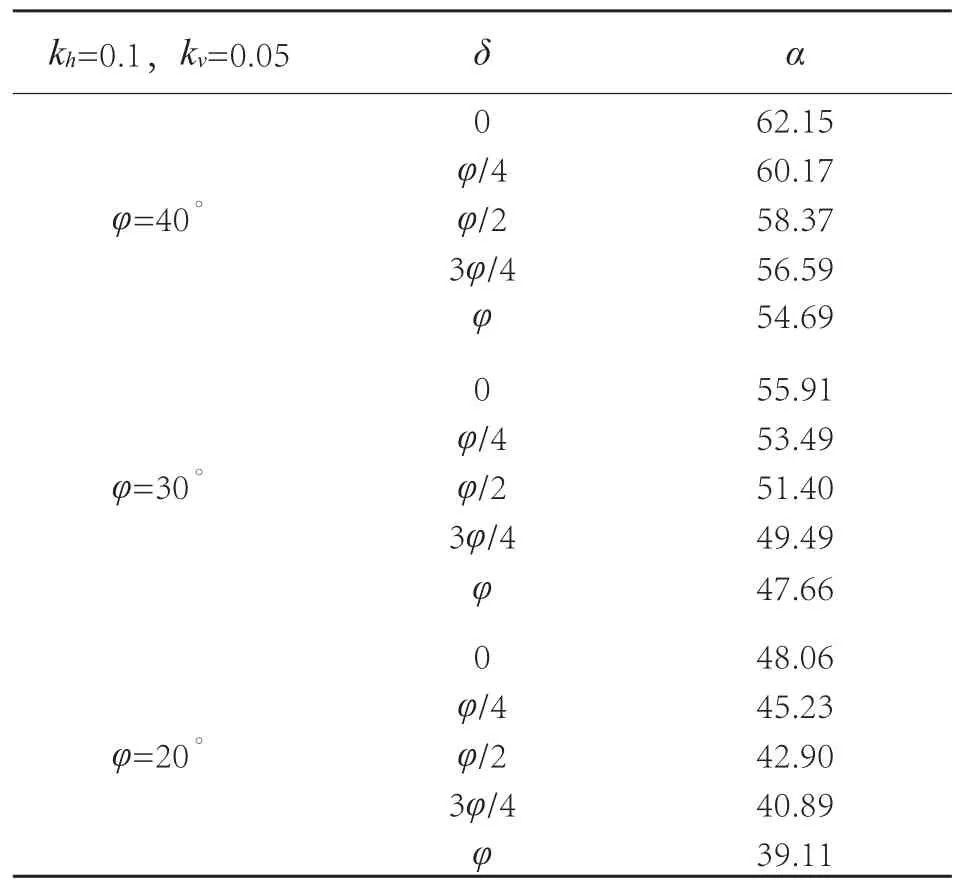
表2 临界破裂角随填土内摩擦角以及挡土与填土之间摩擦角的变化Tab. 2 Critical fracture angle with the angle of internal friction of soil and the change of friction angle between retaining and backf ll

图2 临界破裂角随挡土墙倾角的变化Fig.2 Variation of critical rupture angle with inclination of retaining wall
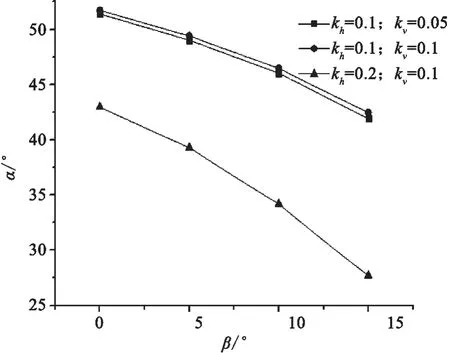
图3 临界破裂角随超载角的变化Fig.3 Variation of critical rupture angle with overload angle
5.1.4 挡土墙后填土超载角对破裂角的影响
取挡土墙后填土内摩擦角φ=30°,挡土墙与后填土之间摩擦角δ=15°,挡土墙后填土超载角β从0°变化到15°,临界破裂角随墙后超载角变化线如图3。从图3中可以看出,随着超载角的增大,临界破裂角随之减小;当水平地震力系数增大时,超载角对破裂角的影响变大。
5.2 主动土压力系数
5.2.1 地震力系数对主动土压力系数的影响
取挡土墙后填土内摩擦角φ=30°,挡土墙与后填土之间的摩擦角δ=15°,挡土墙倾角θ=5°,超载角 β=0。 当 kh=0.1、0.15、0.2,kv/kh=-1、-0.5、0、0.5、1时,主动土压力系数随地震力系数变化如图4。从图4中可以看出,随着竖直地震力系数kv的增加,主动土压力系数也随之增加,即竖直地震力向下时,能产生更大的主动土压力;随着水平地震力系数kh的增加,主动土压力系数也随之增加。
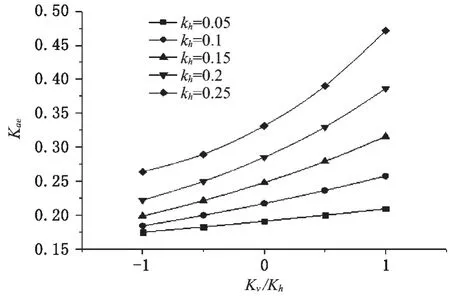
图4 主动土压力系数随地震力系数的变化Fig.4 Variation coefficient of active earth pressure or force coefficient
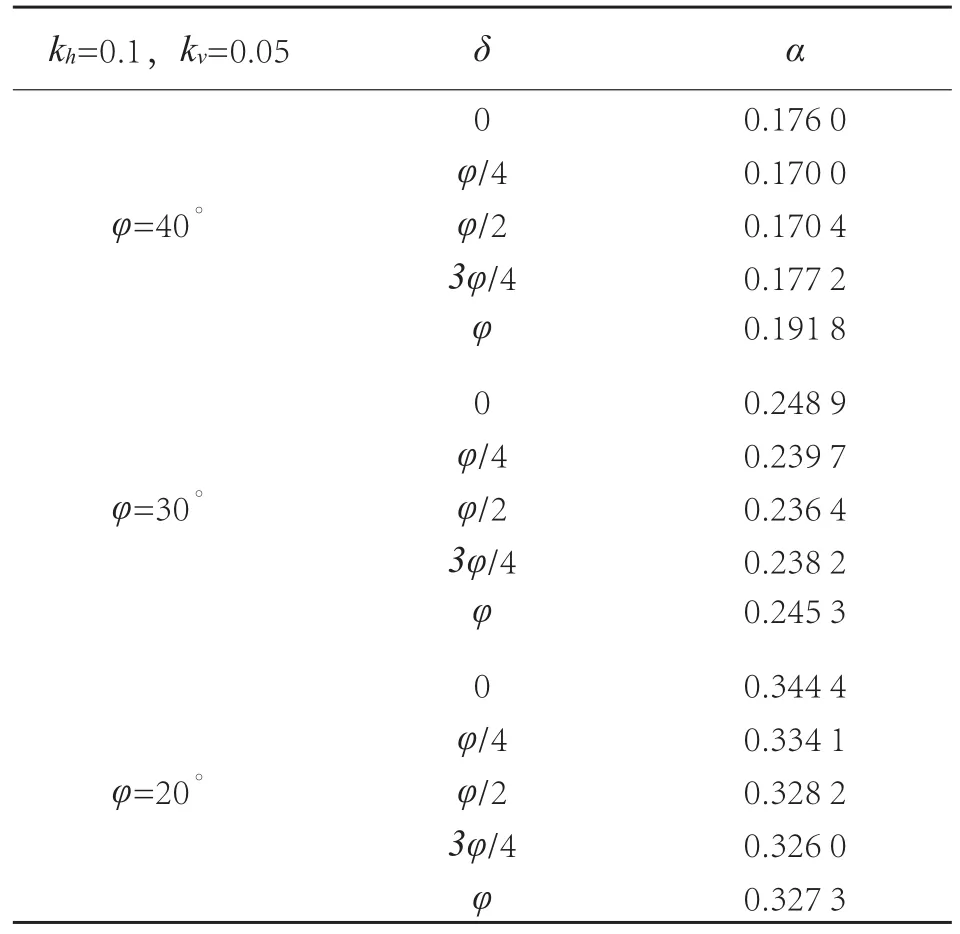
表3 主动土压力系数随填土内摩擦以及挡土与填土之间摩擦角的变化Tab. 3 The coeff cient of active earth pressure along with the internal friction of soil and the friction angle between retaining and earth f ll
5.2.2 填土内摩擦角以及挡土墙与填土之间摩擦角对主动土压力系数的影响
取地震力系数kh=0.1,kv/kh=0.5,挡土墙倾角θ=5°时,超载角β=0°,挡土墙后填土内摩擦角φ=20°、30°、40°,挡土墙与后填土之间的摩擦角δ=0°、φ/4、φ/2、3φ/4、φ 时,主动土压力系数随填土内摩擦角及挡土墙与填土间内摩擦角变化情况如表3所示。从表3中可以看出,随着挡土墙后填土内摩擦角φ的增大,主动土压力系数Kae在随之减小;随着挡土墙与填土之间的摩擦角δ的增大,主动土压力系数Kae为一个先减小然后增大的趋势。

图5 主动土压力系数随挡土墙倾角的变化Fig.5 Variation of active earth pressure coefficient with inclination of retaining wall

图6 主动土压力系数随超载角的变化Fig.6 Variation of active earth pressure coefficient with overloading angle
5.2.3 挡土墙倾角对主动土压力系数的影响
取挡土墙后填土内摩擦角φ=30°,挡土墙与后填土之间的摩擦角δ=15°,超载角β=0°。挡土墙倾角θ从0°变化到25°,主动土压力系数随挡土墙倾角变化线如图5。从图5中可以看出,随着挡土墙倾角的增大,主动土压力系数Kae也随之增大。
5.2.4 挡土墙后填土超载角对主动土压力系数的影响
取挡土墙后填土内摩擦角φ=30°,挡土墙与后填土之间的摩擦角δ =15°,挡土墙后填土超载角β从0°变化到15°,主动土压力系数随墙后超载角变化线如图6。从图6中可以看出,主动土压力系数随着超载角的增大而增大,且当超载角β >10°时,增大幅度加剧,超载角对主动土压力系数的影响增大。
6 结论
1)考虑后填土介质的粘弹特性及自由表面零应力这个边界条件后,所计算出的临界破裂角较现有拟动力法所计算结果小,并发现竖直地震加速度对现有拟动力法放大系数影响较大。
2)水平地震力对临界破裂角以及主动土压力影响大,竖直地震力对临界破裂角以及主动土压力影响小。
3)临界破裂角随着竖直地震力系数、后填土的内摩擦角以及挡土墙倾角的增大而增大,随水平加速度、挡土与填土之间摩擦角以及超载角的增大而减小。
4)主动土压力随着地震力系数、挡土墙倾角以及超载角的增大而增大,随着填土的内摩擦角的增大而减小,随着填土与挡土墙之间的摩擦角的增大先减小后增大。
[1]陈奕柏,谢洪波,柯才桐,等.地震条件下黏性土挡土墙土压力分析[J].岩土力学,2014,35(12):3396-3402.
[2]CHOUDHURY D,SINGH S.New approach for estimation of static and seismic active earth pressure[J]. Geotechnical and Geological Engineering,2006,24(1):117-127.
[3]张国祥.地震条件下挡土墙主动土压力及其分布的新分析法[J].岩土力学,2014,32(2):334-339.
[4]杨 剑,高玉峰,程永锋,等.地震条件下倾斜挡土墙被动土压力研究[J].岩土工程学报,2009,31(9):1391-1397.
[5]夏唐代,孔祥冰,王志凯,等.挡土墙后黏性土的地震主动土压力分析[J].岩石力学与工程学报, 2012,31(Z1):3188-3195.
[6]STEEDMAN R S,ZENG X.The influence of phase on the calculation of pseudo-static earth pressure on a retaining wall[J]. Geotechnique,1990,40(1):103-112.
[7]CHOUDHURY D,KATDARE A D. New approach to determine seismic passive resistance on retaining walls considering seismic waves[J]. Int. J. GeomechGeomech,2013:852-860.
[8]杨海清,杨秀明,周小平.地震作用下挡土墙主动土压力及转动位移分析[J].岩土力学,2012,33(2):139-144.
[9]黄 睿,夏唐代,房 凯,等.竖向稳定渗流条件下的地震主动土压力分析[J].岩土力学,2014,35(9):2522-2528.
[10]BELLEZZA I. Seismic active earth pressure on walls using a newpseudo-dynamic approach[J]. Geotech.Geol.Eng,2015,33(4):795–812.
[11]PAIN A,CHOUDHURY D,BHATTACHARYYA S K. Seismic stability of retaining wall–soil sliding interaction using modified pseudodynamic method[J]. Geotechnique Lett,2015,5(1):56–61.
[12]BELLEZZA I. A new pseudo-dynamic approach for seismic active soil thrust [J]. Geotech. Geol. Eng,2014,32(2):561–576.
[13]王 浩,董建华,王永胜,等.挡土墙地震土压力的拟动力法[J].振动与冲击,2016,33(18):128-133.
[14]孙树林,时冬冬,秦鲜玮,等.库岸加筋土挡墙在地震和涌浪作用下的稳定性分析[J].科学技术与工程,2015,15(12):92-97.
Active earth pressure of retaining wall based on modified pseudo-dynamic method
ZHANG Lei1,SUN Shulin1,2,CHU Hao1,DING Wei1
(1.College of Earth Sciences and Engineering,Hohai University,Nanjing 210098 China; 2. State Key Of Hydrology-Water resources And Hydraulic Engineering,Hohai University,Nanjing 210098 China)
The pseudo dynamic method is one of the most common methods to obtain the earth pressure under seismic conditions. However, this method often ignores the viscoelastic characteristics of the backfill medium and boundary condition with the zero stress on the free surface. In order to remedy the deficiency of the existing pseudo dynamic method, in this paper, the viscoelastic properties of seismic wave propagating medium are considered to improve original pseudo-dynamic methods;Then the calculation formula of the active earth pressure of the inclined retaining wall with overload angle and the fracture angle under the critical failure are derived, and the influences of overloading angle, seismic force coefficient and other parameters on the critical rupture angle and the coefficient of active earth pressure are analyzed. The results show that the critical rupture angle increases with the increase of vertical seismic force coefficient; the horizontal earthquake force coefficient, overloading angle, internal friction angle and retaining wall inclination have great influence on the design of retaining wall.
Earthquake; Retaining wall; Active earth pressure;Critical rupture angle; Modified pseudo dynamic method
TU4
A
1673-9469(2017)03-0032-06
10.3969/j.issn.1673-9469.2017.03.007
2017-06-21
国家重点实验室开放研究基金资助项目(2005408911);留学回国人员科研启动基金资助项目(20071108)
张磊(1993-),男,重庆人,硕士,从事边坡、挡土墙、地质灾害防治方面的研究。

