积分计算中的递推式及其解法探讨

(山东科技大学 山东 青岛 266590)

积分计算中的递推式及其解法探讨

王雪建

(山东科技大学山东青岛266590)

积分递推式是探究积分求解问题中不可避免的问题。积分递推式是积分求解问题中的一把钥匙，对研究各类积分有着至关重要的作用。本文整理并归纳高等数学中常见递推式，用分部积分法,拆项法等基本解法导出积分的递推式。为了使读者更加容易读懂本篇文章，本文就积分递推式的应用加以说明,列举经典而实际的例题，使学生加深对递推公式和解题方法的认识,开发学生解题能力和技巧,在学习和推论中体会高等数学的乐趣。

积分递推式；不定积分；欧拉积分

一、绪论

(一)研究背景

积分递推式问题归根结底是积分的计算问题。积分问题是微分问题的逆运算，即知道了函数的导函数，反求原函数。在实际应用上，积分的作用远远不止这些，它一般被大量应用于求和问题，常用的就是求曲边三角形的面积。积分递推式巧妙的解决了复杂的积分求和问题，这巧妙的求解方法是积分特殊的性质决定的。积分问题最早起源于极限和微积分的问题。

(二)研究意义

在大学中的高等数学中，积分的递推公式证明以及推导问题，和一般的计算题和应用题相比，证明过程对基础一般的学生来说是很困难的，本文的写作目的也是利用分部积分，换元积分，拆项积分等方法推导出积分递推式，解决每一类可能遇见的积分递推式问题，使大家能够快速的找准解决问题的办法，更容易理解推导过程。积分递推式的推导结果用来解决实际问题即积分计算问题。本文就积分递推式的应用加以说明。

(三)积分递推式定义

积分递推公式没有明确定义，相对明确的定义出自于2007年，在高等教育出版社出版的《经济数学-微积分》第二版。提到一般函数递推公式递推法的基本定义：当被积的函数是一个简单函数的高次幂函数时，我们可以恰当选择u′、v′，通过一系列积分法则如分部积分拆项积分等方法，得到这个简单函数的高次幂函数和低次幂函数的内在关系，这个关系就是所谓的递推公式，这个推导过程称作递推法。

二、(不)定积分中常见积分递推式及解法探讨

解决积分中递推公式问题我们最多的采用分部积分法和换元积分法。其它方法本章会另外加以说明。

(一)分部积分法与积分递推式

引理:对于用分布积分法解决积分问题有其必要的前提条件，分部积分法的公式和应该满足的条件：设f(x)，g(x)在[a,b]上有连续的导数，则

含ex型积分递推式

被积函数满足分部积分法条件，采用分部积分法：

=xnex-nIn-1,

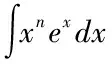
In=xnex-nIn-1.

(2.1)

(二)换元积分法与积分递推式

引理:对于换元积分法解决积分问题有其必要的前提条件，换元积分法的公式和应该满足的条件：

设1.f(x)在[a,b]上连续；2.φ(t)在[a,b]上有连续的导数，其中a=φ(α)，b=φ(β)，

a≤φ(t)≤bt∈[α,β]，且φ′(t)在(α,β)内保持定号。则：

特殊三角函数积分

被积函数满足换元积分条件，采用换元积分法，

令t=arcsinx，则x=sint

则有

=tnsint+ntn-1·cost-n(n-1)In-2

于是

(2.2)

三、解法分析

不论是分式函数还是三角函数亦或是一般简单函数，如果被积函数的次数较高时，在用一般的方法求解中，求解过程会相当繁琐，结果的形式也相当较复杂，并且不能保证每一部的正确性。本文的目的便是建立积分中可能遇见的各种函数的积分递推公式，并总结其解法探讨，使我们更加容易分析运用积分递推式，从而用积分递推公式求解各类积分问题。

本文我们在求解定积分和不定积分的递推式过程中使用最多的方法是换元积分法，分部积分法，拆项法等。我们采用分部积分法求解各类不定积分的积分递推式，但是当被积函数是一般三角函数时，我们一般用分部积分法，当被积函数是反正弦反余弦等函数时我们用换元积分会更加容易些。

四、小结

积分递推式是一把钥匙，一把轻松开启积分计算大门的钥匙。若采积分递推关系的方法来解决积分计算问题,会大大减少计算时间。本文整理并归纳各个大学高等数学中关于不定积分中常见递推公式的定义与常见类型。整理并归纳高等数学中常见递推式，用分部积分法,拆项法等基本解法导出积分的递推式。使学生加深对递推公式和解题方法的认识,开发学生解题能力和技巧,在学习和推论中体会高等数学的乐趣。

[1]华东师大数学系.数学分析[M].北京:高等教育出版社,2001.

[2]刘玉琏，傅沛仁.数学分析[M].北京:高等教育出版社,1998.

[3]李文荣.分析中的问题研究[M].北京:中国工人出版社,2001.

王雪建(1991-)，男，山东滨州，硕士研究生，山东科技大学，研究方向图像处理。