高功率光纤中传输光模式与其波长相关性研究∗
梁井川 冯国英 张澍霖 兰斌 周寿桓
1)(四川大学电子信息学院,激光微纳工程研究所,成都 610064)
2)(华北光电技术研究所,北京 100015)
高功率光纤中传输光模式与其波长相关性研究∗
梁井川1)2)冯国英1)†张澍霖1)兰斌1)周寿桓1)2)
1)(四川大学电子信息学院,激光微纳工程研究所,成都 610064)
2)(华北光电技术研究所,北京 100015)
针对高功率光纤激光模式诊断和光谱诊断的需求,研究了光纤中传输模式的波长相关性,数值计算了光纤中各个模式的模场分布随波长的变化曲线及相应的光束质量,采用双傅里叶变换F2法实际测量了光纤模式成分与波长的关系曲线.结果表明,光纤中各个模式的模场分布随波长变化,波长越长,模场面积越大;模式的光束质量随波长变化不大,但在截止频率附近明显变差;光纤中各个模式的功率占比与波长有关.
光纤模式,基于空间域和频率傅里叶变换的F2法,群时延差异,光谱干涉
1 引 言
高功率光纤激光器和放大器因其良好的稳定性和灵活性而被广泛应用.为了提高光纤激光器的功率,需要增大光纤纤芯直径,实现较大的有效模场面积和减少非线性效应[1].但是,这样会使光纤激发的高阶模式数量增加.通常使用光子晶体光纤或者弯曲大模场光纤实现高功率激光器的单模输出[2−5].为了实现光纤高功率激光器和放大器,需要尽可能地实现大模场光纤的单模运行抑制高阶模式.光纤激光器在高功率输出时,由于非线性、热应力梯度和拉曼效应作用下会使得光谱出现漂移或展宽现象[6,7].不同波长在特定的光纤中传播时会激发不同的模式,当高功率运转时会出现模式成分转换的现象[8,9].单模工作时光束的M2因子不为1,而是大于1[10].实现M2因子接近于1的光纤激光不是单模输出[10−12].因此,在光纤激光器的研究和制造中对光纤模式进行精确测量和分析是非常重要的.目前学术界已经提出C2成像法[13]、低相干干涉法[14],CGH成像法[15]、波前分析法[16]、空间频谱成像法[17−20](简称为S2法)和两次傅里叶变换法[21](简称F2法)等模式分解技术.总体分为:频域相干法和时域相干法.时域相干法基于空间移动产生时间延迟使得模式间分区域相干;频域相干法则是基于各个模式间的群速度延迟及干涉来进行测量.在测量光纤激光光束质量M2因子和模式时,人们常常回避波长的影响,若光束有一定的谱宽,通常就选用平均波长来描述该光束的波长.当需要测量光纤输出超连续谱的光束质量时,通常会选用窄带滤光片滤出光谱再进行光束质量的测量,这带来了光束质量表征的不确定性.F2法能够在不知道光纤特征参数的情况下,同时测量出光纤中传输模式的种类和模式功率成分;该方法不要求较高精度的实验移动平移台,而且灵敏度高;F2法采集模场空间频谱域分布信号进行模式的分析,可在高功率下工作.为此,本文基于F2法开展了光纤模式的波长相关性的理论和实验研究,分析光纤模式与激光波长的内禀关系.
2 光纤模式理论
纤芯半径为a的光纤中形成的导波模式,对应存在一个有效折射率ne=β/k0,β和k0分别表示有效传播常数和真空传播波数,有效折射率介于包层折射率n2和纤芯折射率n1之间.阶跃弱导光纤中传播的模式使用线偏振模式(LPmn)进行描述.设光场的偏振方向为y,则阶跃弱导光纤中的模式场的贝塞尔方程表达式为[22,23]:

其中r表示光纤半径,Jm和Km分别为m阶虚宗量贝塞尔函数和修正贝塞尔函数(m=0,1,2,···),U和W分别表示归一化横向相位参数和归一化横向衰减参数.通过电场和磁场的边界条件可以得到光纤中模式场包层和纤芯的连续性分布,结合贝塞尔函数性质从而推导出LPmn模式本征方程[10]:

通过数值解可以得到对应LP模式的场分布.为了能够更好地描述和分析光纤,一般都采用归一化工作频率V来概括模式的直接相关关系.波长为λ的归一化工作频率为

对于弱导阶跃光纤而言,能够使用标量近似解法和电磁场边界条件得到其模场本征方程.求解模场本征方程可以得到线偏振模式的有效折射率随归一化频率的变化,从而得到光纤在特定波长下所支持的模式类型和数量.根据文献[22]可知,归一化工作频率变化对应的光纤模式数量也会变化.结合(3)式可以看出,光纤一定时,波长是引起归一化频率变化的直接原因.
本文使用F2法进行光纤模式波长相关性的研究.由文献[21]可知,设光纤模式混合光场:
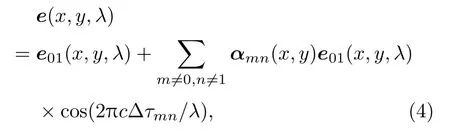
其中,c表示光速,e01(x,y,λ)为LP01模式场分布,αmn和∆τmn分别表示LPmn模式与LP01模式干涉的相关系数和相对群时延.设透镜焦距为f,在透镜的后焦面空间坐标为(x′,y′),则混合场经过透镜傅里叶变换后得到的输出场为

式中对应的傅里叶变换关系为,F{e(x,y,λ)}=EF(fx,fy,λ),F{e01(x,y,λ)}=E01,F(fx,fy,λ),F{emn(x,y,λ)}=Emn,F(fx,fy,λ),F{αmn(x,y)}=Amn,F(fx,fy).
那么,透镜傅里叶变换后的光强分布可表示为

其中,I01,F,IF分别为空间傅里叶变换后的基模和总光场的强度,函数Bmn满足条件:
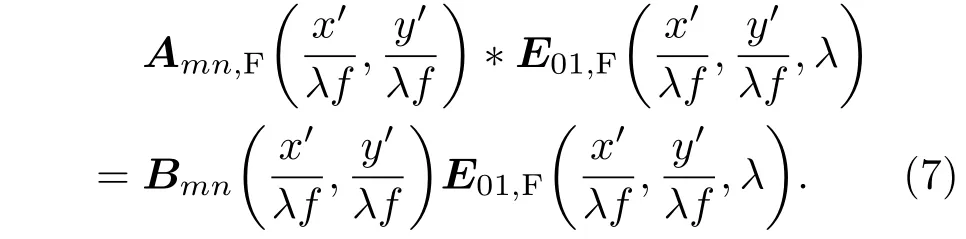

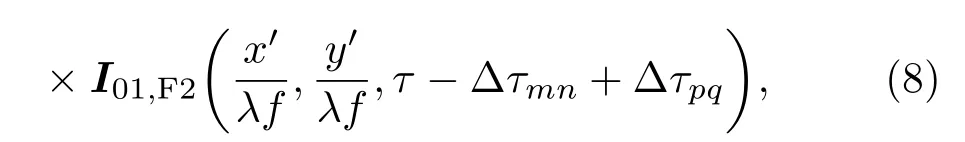
定义Tmn为IF2在相对群时延分别为∆τmn和0的比值[18]:

可得Bmn与Tmn关系,
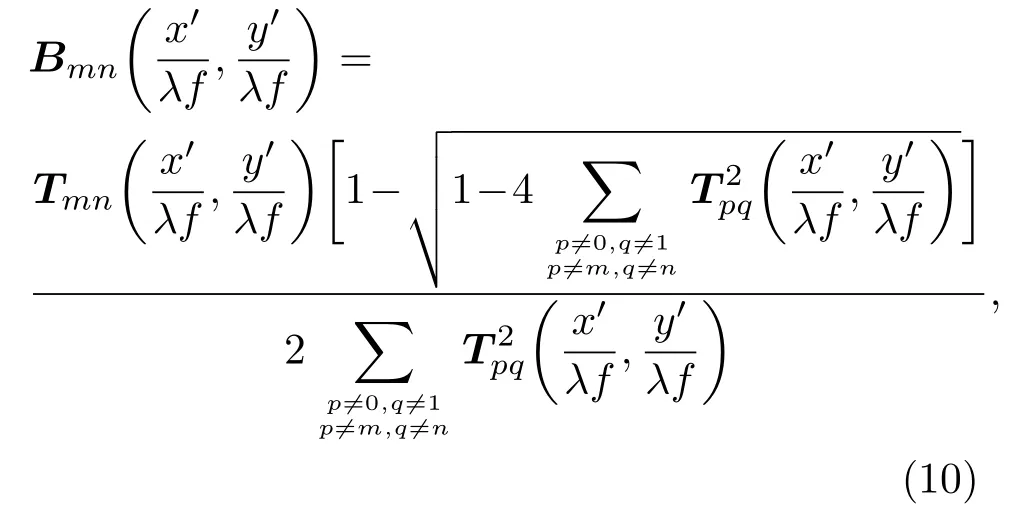
从而得到基模和高阶模两次傅里叶变换后的强度分布,

其中,Itotal,F2(x,y)为给定点(x,y)的光谱强度积分值.
对应的基模模式和高阶模式占光纤输出总光场的功率比R01和Rmn为:

这样我们就可以得到基模和高阶模相对总光场的功率比.(8)式中的第三项代表高阶模之间的干涉,它们的比值Tmn,pq定义为

如果高阶模相对基模较弱,可以忽略高阶模之间的干涉,

(9)和(15)式可以写成如下形式:

所以,通过光谱仪记录空间和频谱信息,能够计算分解出光纤中传播的模式和模式对应的功率比.
3 数值模拟
根据(3)式可知,当弱导阶跃光纤折射率及其分布一定时,波长与归一化频率成反比.随着波长变化时归一化工作频率相应出现变化,导致光光纤中的模式受到影响.图1分别给出了在不同波长激发条件下的LP01,LP02,LP12和LP11模式在x方向的功率归一化场强分布.从图中能够清晰地看到,相同功率条件下的同种模式随着波长的增加其模式场强宽度也在增加,但其峰值功率却在不断下降.
当一种光纤模式的能量不能够束缚在纤芯中传播时,该模式的能量会在光纤的传输下逐渐从纤芯向包层泄露,该模式最终能量完全耗尽而消失.本文使用二阶矩计算了不同波长下不同模式的直径宽度Wx.如图2(a)所示,随着波长增加,光纤中的模式分布和模式x方向上场强分布宽度Wx也在增加.而在图2(a)中有些模式随着波长变化直径突然变得很大,之后该模式对应的Wx就消失了.根据(3)式可知,波长与归一化频率成反比,由文献[22]可知光纤中的模式会因为波长增加出现的归一化频率减小而到达截至频率.当归一化频率小于截至频率后,模式场就会随着传输逐渐从纤芯辐射到包层直至完全消失.当光纤工作波长变大时,直接影响该光纤中模式种类和数量的变化,模式数量相对还会变少.所以,波长越长,越容易实现少模或者单模光纤激光输出.
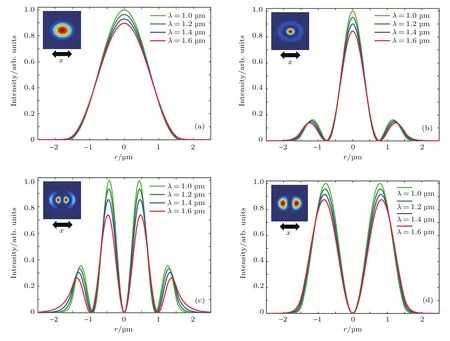
图1 (网刊彩色)不同波长下(a)LP01,(b)LP02,(c)LP12和(d)LP11模式在x方向上的功率归一化强度Fig.1.(color online)Normalized intensity distribution of di ff erent modes with di ff erent wavelength in the x direction:(a)LP01mode;(b)LP02mode;(c)LP12mode;(d)LP11mode.

图2 (网刊彩色)LPmn模式在x方向的(a)强度分布直径Wx和(b)光束质量随波长的变化Fig.2.(color online)The diameter Wx(a)and beam quality(b)of LPmnmode change with wavelength.

图3 (网刊彩色)中心波长为1020—1070 nm频谱下的模式分解结果 (a)模式群时延;(b)模式功率成分Fig.3.(color online)The mode decomposition results with di ff erent central wavelength between 1020 nm and 1070 nm:(a)The group delay of modes;(b)the power content of modes.
通过双曲线拟合法[11]对不同波长条件下激发的光纤模式对应的光束质量(M2)值进行计算.如图2(b)所示,模式的光束质量随波长变化不大,但在截止频率附近却明显变差.因为随着波长的不断增加,模式的归一化频率最终小于其归一化截止频率值.从图2可知,当模场直径在某一波长出现跳变时,对应模式的M2值也会因为模式光场直径变大而相应出现跳跃性增加.
光纤中传播的高阶模式,可以通过它们和基模的群时延差体现.使用宽谱光源在光纤中传播时,频谱产生干涉花样,通过一段光纤传输距离后的高阶模式和基模干涉条纹将清晰可见[18,21].对于阶跃弱导光纤模式的理论分析可知,光纤中存在的模式会随着波长的改变而出现变动.
改变用于F2法测量中所用到的宽谱光源的中心波长和谱宽分别进行模拟实验.宽谱光源的谱宽为20 nm,中心波长以步长为10 nm逐渐从1020增加到1070 nm.假定光纤弯曲对高阶模式抑制,光纤中仅仅激发出LP01,LP11和LP21三种主要模式.通过在不同中心波长光源下对输出光进行F2法模式分解进行数值模拟.模拟实验结果如图3所示,通过F2法模式分解成功分解出LP01,LP11和LP21三种模式.
当中心波长从1020 nm以间隔为10 nm逐渐增加到1070 nm时,LP11模式和LP21模式之间出现了明显的小尖峰.这些小尖峰在文献[20]中进行了具体分析,它们属于高阶模式干涉虚假尖峰.在对应小尖峰位置,根据模式解析算法绘制出相应的“模式花样”,得到如图3中所示LP11+LP21模式花样.图3(b)给出了F2法分解出的模式对应的功率成分.随中心波长的不断增加,模式对应的功率成分出现了轻微的变化,但是变化量不大.通过三条曲线数据点能够发现,所有模式功率成分相加等于100%.

图4 (网刊彩色)中心波长为1064 nm的不同光源谱宽下的模式分解Fig.4.(color online)Optical fi ber modes resolution result use the source with di ff erent wavelength bandwidth,and the central wavelength of the source is 1064 nm.
由图2可知,当波长的变化导致某一个高阶模式小于其归一化工作截至频率时,该模式将不能够在光纤中进行稳定传输.当光源谱宽变化时,使用存在LP01,LP11,LP21和LP02模式的光纤进行谱宽变化的F2模拟实验.结果如图4所示,光源中心波长为1064 nm,谱宽从5 nm逐渐增加到20 nm分解出的模式数量和模式功率成分出现了变化.从图4中可知,当仅存在5 nm的谱宽时,只分解出LP01模式和LP11模式.波长带宽增加到10 nm之后,又分解出了LP21模式和LP02模式.通过模式分解得到的模式成分可知,所有模式功率成分都满足模式叠加性.
4 实验及测量结果
由于色散,光纤中传播的模式会出现不同时间差异性即群时延差.宽谱光源中包含许多不同波长成分的光,能够在光纤中激发出稳定传播的线偏振模式.结合群时延差异、空间和频谱信息,能把光纤空间中混合传播的复合模式进行分解.本文采用F2法对大模场阶跃光纤进行了模式测量,F2法实验装置原理如图5所示.实验中使用了一根长度为3 m,纤芯直径为30µm的大模场光纤作为待测光纤(UTF);光源为放大自发辐射光源(Souse:ASE),中心波长和谱宽分别为1064 nm和20 nm.光源发出的光依次经过UTF、光纤准直镜(Lens)和起偏器得到准平行光.利用固定在电动三维(3D)平移台上的单模光纤探针在光束横截面上进行二维扫描,探针所在空间位置(x,y)处的光信息并通过单模光纤传输进入光谱分析仪(OSA)进行记录.最终通过电脑(CP)接受并处理OSA记录的空间频谱信息,分解出光纤中传播的模式.
选取中心波长和谱宽分别为1064 nm和20 nm的光对待测光纤进行模式分解实验.在实验的过程中,为了防止光纤入射端光入射条件引起大模场光纤中未形成模式的杂波到达输出端面而影响实验结果,对大模场光纤进行了40 cm直径的缠绕弯曲.通过实验数据计算得到的实验结果如图5所示,可以看到,对20 nm谱宽波长实验结果进行计算可以得到LP01模、LP11模、LP21模和LP02模;基模占据了主要成分,光纤激发的高阶模式成分相对较少.根据模式之间的群时延大小和高阶模式之间相干性可知,在图5中的a和b标记处并不是光纤中真实存在的高阶模式尖峰,它们是高阶模式相干产生的虚假模式尖峰.
对20 nm谱宽光源进入待测光纤后的输出光空间频谱信息进行波长分段分析.中心波长为1064 nm,选取谱宽分别为5,10,15和20 nm对光纤进行模式分解.图6给出了不同带宽情况下的模式和功率百分比.实验结果表明,所测量光纤在不同谱宽条件下基模成分都占据主导,而高阶模式数量随着谱宽的增加而增加,且在不同的谱宽条件下相同模式所占成分都不相同,实验结果与模拟结果相一致.
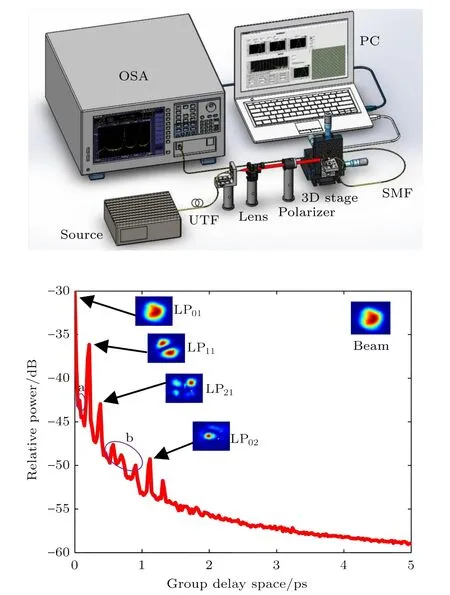
图5 (网刊彩色)F2法实验装置原理示意图和实验结果Fig.5.(color online)Experimental setup and experimental results of F2technology.

图6 (网刊彩色)不同谱宽下的实验分解出的模式成分和花样Fig.6.(color online)Optical fi ber mode patterns and content of di ff erent bandwidth experimental situation.
在谱宽为5 nm的情况下依然能够激发光纤中的高阶模式LP11,而且没有其他高阶模式成分.以5 nm频谱宽度来对测试光纤进行模式分解实验,实验所选取频谱波长范围分别为1054—1059,1059—1064,1064—1069和1069—1074 nm,实验结果如图7所示.在不同的频谱范围且谱宽都为5 nm的情况下,实验结果中只存在基模LP01和高阶模式LP11,基模依旧占据主要成分.通过实验计算得到,在4种不同的频谱下得到的LP01模式成分占比分别为89.87%,89.76%,89.83%和89.35%,它们几乎相等.这与我们之前模拟的结果相一致,频谱宽度一定时,波长轻量级变化后模式成分变化量较小.

图7 (网刊彩色)相同频谱宽度、不同中心波长下的模式分解Fig.7.(color online)Optical fi ber modes resolution experimental result with the same frequency bandwidth and di ff erent central wavelength.
5 结 论
对光纤模式的波长相关性进行了模拟仿真和实验验证.通过理论仿真发现,光纤结构参数一定时,高阶模式数量会随着波长的增大而减小;波长越大,光纤中的同一种高阶模式场强分布将从中心向包层中扩展,对应光束质量变差,甚至达到截至条件后该模式不能被激发.光纤中模式成分也会随着中心波长和频谱带宽的变化而变化.本文搭建的F2法实验装置测量了大模场阶跃光纤的模式,实验结果验证了波长与光纤模式的相关性.
[1]Zhou P,Liu Z J,Xu X J,Chen Z L 2008Appl.Opt.47 3350
[2]Koplow J P,Kliner D A V,Goldberg L 2000Opt.Lett.25 442
[3]Nicholson J W,Fini J M,Yablon A D,Westbrook P S,Feder K,Headley C 2007Opt.Lett.32 2562
[4]Zheng X J,Ren G B,Huang L,Zheng H L 2016Acta Phys.Sin.65 064208(in Chinese)[郑兴娟,任国斌,黄琳,郑鹤玲2016物理学报65 064208]
[5]Limpert J,Schreiber T,Nolte S,Zellmer H,Tünnermann A,Iliew R,Lederer F,Broeng J,Vienne G,Petersson A,Jakobsen C 2003Opt.Express11 818
[6]Olshansky R,Keck D B 1976Appl.Opt.15 483
[7]Feng Y,Taylor L R,Calia D B 2009Opt.Express17 23678
[8]Jauregui C,Eidam T,Otto H J,Stutzki F,Jansen F,Limpert J,Tünnermann A 2012Opt.Express20 12912
[9]Stutzki F,Otto H J,Jansen F,Gaida C,Jauregui C,Limpert J,Tünnermann A 2011Opt.Lett.36 4572
[10]Yoda H,Polynkin P,Mansuripur M 2006J.Lightwave Technol.24 1350
[11]Fu Y Q,Feng G Y,Zhang D Y,Chen J G,Zhou S H 2010Optik121 452
[12]Wielandy S 2007Opt.Express15 15402
[13]Schimpf D N,Barankov R A,Ramachandran S 2011Opt.Express19 13008
[14]Nandi P,Chen Z L,Witkowska A,Wadsworth W J,Birks T A,Knight J C 2009Opt.Lett.34 1123
[15]Kaiser T,Flamm D,Schröter S,Duparré M 2009Opt.Express17 9347
[16]Paurisse M,Lévèque L,Hanna M,Druon F,Georges P 2012Opt.Express20 4074
[17]Hu L L,Feng G Y,Dong Z L 2015Infrar.Laser Eng.44 2517(in Chinese)[胡丽荔,冯国英,董哲良 2015红外与激光工程44 2517]
[18]Nicholson J W,Yablon A D,Ramachandran S,Ghalmi S 2008Opt.Express16 7233
[19]Nicholson J W,Yablon A D,Fini J M,Mermelstein M D 2009IEEE J.Quantum Electron.15 61
[20]Nguyen D M,Blin S,Nguyen T N,Le S D,Provino L,Thual M,Chartier T 2012Appl.Opt.51 450
[21]Zhang S L,Feng G Y,Zhou S H 2016Acta Phys.Sin.65 154202(in Chinese)[张澍霖,冯国英,周寿桓 2016物理学报65 154202]
[22]Gloge D 1971Appl.Opt.10 2252
[23]Tan X F,Liu X L,Zhao W,Li C,Wang Y S,Li J F 2013Opt.Commun.294 148
Analysis of wavelength dependence of mode in high power fi ber laser∗
Liang Jing-Chuan1)2)Feng Guo-Ying1)†Zhang Shu-Lin1)Lan Bin1)Zhou Shou-Huan1)2)
1)(Institute of Laser and Micro/Nano Engineering,College of Electronics and Information Engineering,Sichuan University,Chengdu 610064,China)
2)(North China Research Institute of Electro-Optics,Beijing 100015,China)
High power fi ber lasers and ampli fi ers are widely used in the scienti fi c and industrial fi eld.In order to meet the requirements for high output powers the e ff ective area of fi bers becomes larger and larger to reduce optical nonlinearities.With the increase of e ff ective area,the number of high-order modes will increase.In the case of high output power,the spectral shift and broadening of the optical fi ber will also a ff ect the modal number and content.The number and content of fi ber modes a ff ect the pointing stablity and quality of the laser beam.TheM2-parameter is commonly used to de fi ne the quality of the laser beam,but a smallM2number is not guaranteed for single mode operation.Therefore,the relationship between wavelength and transmission mode in fi ber transmission is studied in this paper.We use the spatial and spectral Fourier transform(F2)method to establish a theoretical-experimental method of describing the relationship between wavelength and mode.This method can directly give out the modal content of optical fi bers without any priori parameter such as the properties of fi ber and requirement for setup accuracy.On the one hand,the theoretical modeling of wavelength a ff ects modal content.In the simulation,the sources with the same wavelength bandwidth and di ff erent central wavelengths are used to test the fi ber.The results show that the modal content and number of the fiber change with the wavelength bandwidth and center wavelength.The mode components of the corresponding optical fiber will change after changing the central wavelength.As the spectral width of the light source increases,the number of high-order modes increases.On the other hand,in order to further verify the relationship between wavelength and mode of fi ber,the F2method is used to measure the optical fi ber modal content with di ff erent wavelengths.The fi nal experimental results are in agreement with the theoretical results.The experimental and simulation results show that the mode fi eld distribution of each mode varies with wavelength:the longer the wavelength,the larger the mode fi eld is.The beam quality has little change with the wavelength except for those positions with frequency near the cuto ff frequency,and the power ratio of each mode relates to the wavelength.
fi ber modes,F2method based on spatial and spectral Fourier transform,group delay di ff erence,spectral interference
21 February 2017;revised manuscript
7 July 2017)
(2017年2月21日收到;2017年7月7日收到修改稿)
10.7498/aps.66.194202
∗国家自然科学基金(批准号:11574221)和国家高技术研究发展计划(批准号:JG2011105)资助的课题.
†通信作者.E-mail:guoing_feng@scu.edu.cn
©2017中国物理学会Chinese Physical Society
PACS:42.25.Hz,42.81.–i
10.7498/aps.66.194202
*Project supported by the National Natural Science Foundation of China(Grant No.11574221)and the National High Technology Research and Development Program of China(Grant No.JG2011105).
†Corresponding author.E-mail:guoing_feng@scu.edu.cn

