基于EEMD-Fast ICA-STFT的车用起动电机噪声源识别

龚承启，华春蓉

（西南交通大学 机械工程学院，成都 610031）

基于EEMD-Fast ICA-STFT的车用起动电机噪声源识别

龚承启，华春蓉

（西南交通大学 机械工程学院，成都 610031）

提出基于集成经验模态分解（EEMD）、快速独立分量分析（Fast ICA）和短时傅里叶变换（STFT）的噪声源识别方法，对起动电机噪声信号进行声源识别研究。首先采用集成经验模态分解法将单一通道的电机噪声信号分解为一系列本征模态分量，随后用Fast ICA算法提取独立成分，最后利用短时傅里叶变换良好的时频分析特性，对Fast ICA分离结果进行时频分析，结合时频分析结果和电机噪声的先验知识，确定了各独立分量与电机不同噪声源的对应关系。

声学；电机噪声源；经验模态分解；独立分量分析；短时傅里叶变换

汽车起动电机是汽车的重要零部件之一，在起动时会发出明显的啸叫声，影响汽车的舒适性能，在客户对汽车舒适性能要求越来越高的今天以及汽车频繁起停的交通现状，减小电机起动时的噪声显得尤为重要。噪声源识别技术可以采取针对性的技术减振降噪，更能够在设计阶段对产生噪声的零部件及部位加以控制，实现低噪声设计[1]。

近年来，许多学者对电机噪声源的分离和识别进行了研究：文献[2]采用功率谱法对电机振动信号进行处理，识别出了电机的机械噪声；文献[3]基于波束形成理论，利用十字形阵列识别了整车电机驱动系统的主要噪声源；文献[4]采用自适应共振方法识别出了该天窗电机的噪声电机噪声主要是由轴承内圈滚道划伤、轴向窜动引起；文献[5]通过交流电机的振动和噪声测试，采用频谱分析和阶次分析等方法，识别出了汽车交流发电机在负载工况下的噪声主要是由36阶次电磁噪声引起；文献[6]采用阶次分析法识别出了起动机的异响噪声，同时指出起动机停机阶段的异响噪声与电机的电枢槽数密切相关；

综合目前电机噪声源识别研究现状，由于起动电机在工作时其电枢旋转速度并非处于稳定状态，使所测得的振动噪声信号频率成分在不断变化，在进行传统的频谱分析时，会产生明显的“频率模糊”现象。阵列法虽然能够较好地识别噪声源，但当声源频率很高时，往往使传声阵列非常大，导致设备成本极大增加；阶次分析法对噪声信号的信噪比要求较高，容易受到其它干扰噪声的影响；噪声振动分析法和自适应共振法存在不能处理单一通道噪声信号的问题。

针对以上问题，本文提出了一种基于EEMDFast ICA-STFT的信号处理方法，对采集到的电机单一通道噪声信号进行噪声源识别研究，首先利用集成经验模态分解（EEMD）将电机噪声信号分解为若干个独立的本质模态函数（IMF），随后将EEMD分解得到的与原信号相关性较高IMF分量作为Fast ICA算法的输入，最后利用短时傅里叶变换（STFT）对各个独立分量进行分析，结合时频分析结果有效的识别了电机噪声源。EEMD-Fast ICA-STFT算法流程如图1所示。

图1 EEMD-Fast ICA-STFT算法流程

1 基本理论

1.1 经验模态分解（EEMD）基本原理

EEMD的核心是EMD方法，它是一种高效自适应的信号分解方法，任何时间序列都能分解成一组从高频到低频的均值为零均值分量(IMF)[7]。EEMD方法的步骤如下：

（1）在原信号中添加预定义噪声幅度的白噪声。

（2）对新生成的信号进行EMD分解。

（3）加入固定振幅的不同白噪声并重复上述步骤。

（4）对同阶的分量进行集总平均，即可得到的分解结果。

EEMD通过对测得信号加入白噪声来平滑异常事件，改变原信号极值点分布特性，从而使得分布更加均匀，所求取的包络线中仅包括异常事件或真实信号的包络，该方法能有效抑制异常扰动引起的模态混叠。同时这种方法将多分解结果应用于集总平均计算，降低了模态混叠的机会同时使分解的IMF更有意义。

1.2 独立分量分析（ICA）的概念

ICA是对信号进行盲信号分离的方法，Fast ICA是算法是广泛使用的独立分量分析法之一[8]，设x=(x1，x2，…，xm)T为m维零均值随机观测信号向量，它是由n个未知的零均值独立源信号s=(s1，s2，…，sn)T线性混合而成的，这种线性混合模型可表示为

式中H=[h1，…，hn]为m×n阶满秩源信号混合矩阵；hj为混合矩阵的n维列向量。上式可以写成矩阵形式

为确保ICA模型能够被估计，必须对其进行一定的约束。首先，独立分量也就是源信号，被假定是统计独立的。该假设是ICA能够成立的前提。其次，独立成分必须具有非高斯的分布。如果观测变量具有高斯分布，那么ICA在本质上是不可能实现的。最后，为了简单起见，假定未知的混合矩阵是方阵。也就是说，独立分量的个数与观测向量的个数是相等的，即m=n[9]。

1.4 短时傅里叶变换（STFT）

1946年，Gabor提出了窗口傅里叶变换概念，用一个在时间上可滑移的时窗来进行傅里叶变换，从而实现了在时间域和频率域都具有较好局部性的分析方法，这种方法称为短时傅里叶变换（Short Time Fourier Transform，STFT）。

设h(t)是中心位于τ=0、高度为1、宽度有限的时窗函数，通过h(t)所观察到的信号x(t)的部分是x(t)h(t)。

当h(t)的中心位于τ，由加窗信号x(t)h(t-τ)的变换便产生短时傅里叶变换。

2 EEMD-Fast ICA模型

本文采用了基于EEMD-Fast ICA的模型方法对单一通道的电机噪声信号进行分析研究，由于电机噪声信号的非平稳性以及噪声源的不确定性，EEMD方法可自适应地将电机噪声信号分解为一系列本征模态分量（IMF），随后将EEMD分解得到的IMF作为Fast ICA算法的输入。该方法的优势在于EEMD-Fast ICA模型的采用有效地抑制了EMD方法存在模态混叠的现象，同时也解决了ICA模型要求通道数目必须大于等于噪声源数目的问题。

2.1 模拟仿真

由于EEMD-Fast ICA模型最终会应用到起动电机噪声信号处理中，本文模拟了一组与电机噪声信号相似的仿真信号，电机噪声信号一般是由其转速基频信号及一系列基频的倍频信号的混合组成。如图2所示。

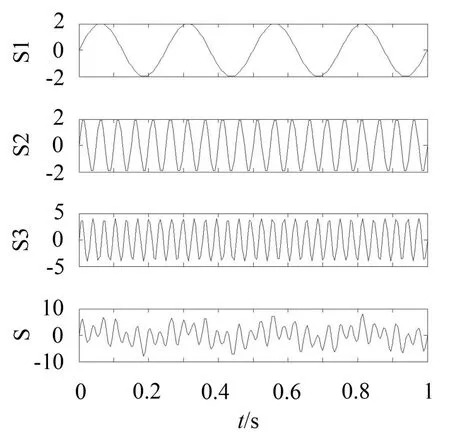
图2 仿真信号及各组成成分时域波形

仿真信号S是一个由三部分组成的混合信号：

以信号仿真信号S作为EEMD-Fast ICA的输入信号，EEMD分解的集成次数为100次，白噪声幅值系数为0.2，最后的分离结果如图3所示。

图3 EEMD-Fast ICA分离结果

对比图2及图3可知，EEMD-Fast ICA的分离结果IC1a、IC2a、IC3a分别对应原仿真信号的S3、S2、S1。仿真信号的分离结果表明，采用EEMD-Fast ICA模型能够较好地恢复出原信号的特征。

3 电机噪声实验布

3.1 测试平台

本次实验在在西南交通大学汽车工程研究所的电机声功率测试实验室内进行，半消声室的截止频率为200 Hz或以下。测试条件及测试对象如下：

（1）采样频率：44 100 Hz；

（2）工作电流：12A直流给工作电机供电；

（3）实验对象：10极永磁直流起动电机，定子为2片磁钢；

（4）实验工况：15 000 r/min空载工况，即电机转频为250 Hz。

3.2 测试系统及测点布置

实验中硬件采用了德国HEAD公司的DATaRec4 DIC24模块，采集软件为Head Recorder。实验中采用了G.R.A.S46AE声压传感器，一个基恩士FS-N系列数字光纤速度传感器。电机的麦克风及速度传感器布置如图4所示，在距电机上方10 cm处布置有声压传感器。

图4 电机噪声测试实验

4 起动电机噪声源识别

4.1 基本分析

图5是电机噪声的时域和频域波形图。从电机噪声频谱图中看出电机噪声频带较宽，特征噪声频率周围存在其它边带频率，严重影响噪声源的分离识别，故需要对电机噪声信号做进一步的处理。

4.2 基于EEMD的电机噪声分解

对电机噪声信号进行EEMD分解，白噪声的幅值系数设置为0.8，集成次数为200。电机噪声信号被分解为14个本征模式分量（IMF）。

由于试验过程中采集的信号夹杂着其他部件及环境产生的噪声信号，同时在EEMD运算过程中的拟合过冲和不足、插值误差等原因也会产生误差，误差会在多次迭代中不断累积，使得信号的分解结果中出现虚假分量，最终分解得到的IMF可分为噪声部分、信号部分和趋势项部分。高频噪声和低频虚假分量与原信号的相关性很小，可以通过皮尔逊相关系数R辨别，R取值范围为［-1，1］，绝对值越大表明相关性越强，其数学表达式为

图5 电机噪声时域及频谱图

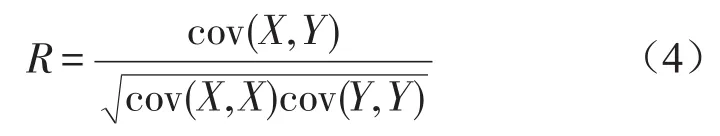
噪声信号经EEMD分解后得到的各IMF与原始信号的皮尔逊相关系数如表1所示。

表1 各个IMF分量的皮尔逊相关系数

然后选择相关性较大的主要的IMF分量，把所关心的IMF和原始信号作为输入源信号，相关系数的阈值取0.2。

4.3 基于Fast ICA-STFT的电机噪声源识别

对选择的IMF分量运用基于负熵极大的固定点算法，即Fast ICA算法，恢复其各独立成分ICs。从图6可以看出，混合信号经Fast ICA算法处理后被分离成6个独立分量，由ICA原理可知，盲源分离算法得到的每一个独立分量都有可能是电机噪声的激励源。由于分离得到的各分量相对应的激励源是不确定的，借助短时傅里叶变换（STFT）良好的时频分辨特性，对分离得到的各分量进行短时傅里叶变换时频分析。

图7－图11是电机单通道噪声信号分离结果中较突出的5个分量，分别为IC2、IC3、IC4、IC5、IC6。结合其对应的时频图，可以看出5个分量均具有较强的周期特性和较准的频率范围，因此，每个分量都对应一个噪声源。

图6 EEMD-Fast ICA分离结果

图7 IC2时频分析结果

由图7可知，独立分量IC2的峰值频率主要集中在5 019 Hz，已知试验工况下该起动电机转速为15 000 r/min左右，转速基频在250 Hz附近，由电机电磁噪声的机理可知，理想条件下电机径向力波的频率特征为电机槽、极数的整数倍阶，电磁噪声特征频率可表示为

式中i为谐波次数；Q为齿槽数；n为电机为转速。

根据（5）式可知5 019 Hz对应于电机转频的20倍频，由时频图可以看出，该频率成分一直持续间断出现，对于10极2槽电机而言，是电机定子、转子槽数的整数倍阶，因此可以判定IC2分量噪声主要来源于电机永磁体磁密和电流基波磁密作用下的电磁激励；

由图8可知，独立分量IC3的峰值频率主要集中在2 509 Hz，由时频图可以看出，该频率成分一直持续间断出现，根据（5）式可知该频率对应于电机转频的10倍频，是电机定、转子槽数的整数倍阶，可以判定IC3分量的噪声来源于电机永磁体磁密和电流基波磁密作用下的电磁激励；

由图9、图11可知，独立分量IC4、IC6的峰值频率主要集中在754 Hz、251 Hz，由时频图可以看出，该频率成分一直持续间断出现，由电机噪声机理可知，电机因转子不平衡产生的机械噪声，其噪声频率一般为电机转频，同时在噪声频谱图中也可能会出现转频的2倍、3倍频，机械噪声的特征频率可表示为

根据公式（6）可知，IC4、IC5分量的峰值频率分别对应于电机转频的3倍频以及电机转频，因此可以判定IC4、IC5分量对应于电机转子不平衡生产生的机械噪声；

图8 IC3时频分析结果

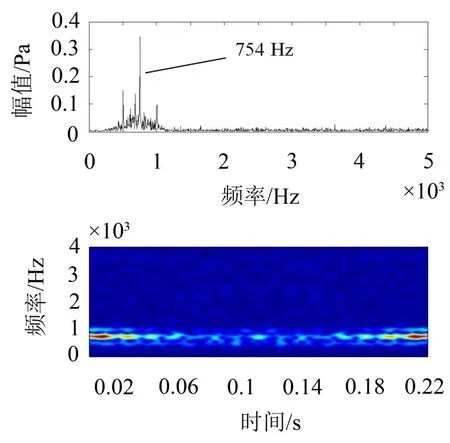
图9 IC4时频分析结果

由图10可知，独立分量IC5的峰值频率主要集中在1 509 Hz，由时频图可以看出，该频率成分一直持续间断出现，根据（5）式可知该频率对应于电机转频的6倍频，是电机定子槽数的3倍，因此可以判定IC5分量的噪声同样来源于电机永磁体磁密和电流基波磁密作用下的电磁激励。

5 结语

本文采用基于EEMD-Fast ICA-STFT的方法对起动电机单一通道噪声信号噪声源识别问题进行了研究，主要结论如下：

（1）该起动电机的噪声分为机械噪声和电磁噪声两部分，机械噪声的主要阶次为1阶、3阶，原因是电机转子不平衡产生的噪声；电磁噪声的主要阶次为6阶、10阶、20阶，中低阶次的电磁激励与理想条件下电磁力特征重合，所贡献的阶次都为电机定子槽数、转子极数的整数倍。

（2）从分离得到独立分量的分析结果来看，每个ICA分量都具有突出的峰值频率，故EEMD-Fast ICA模型的采用在一定程度上抑制了EMD方法存在的模态混叠问题

（3）从电机噪声信号的时频图可以看出，STFT对于电机噪声信号有着较好的时频分辨率，可以更清楚地分析信号的时频特征。

（4）采用基于EEMD-Fast ICA模型可以将单一通道电机噪声信号分解成为一系列具有突出峰值频率的独立分量，每一个独立分量都对应一个电机噪声的激励源，从而实现了对电机噪声源的分离识别，同时在信号的采集过程中无需布置多个声传感器和加速度传感器，使得试验测量更为简单。

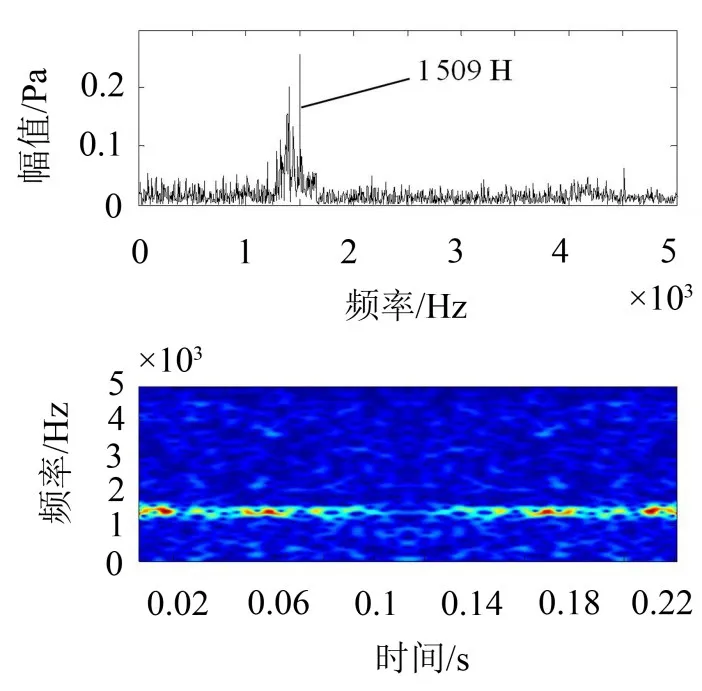
图10 IC5时频分析结果

图11 IC6时频分析结果

[1]陈心昭.噪声源识别技术的进展[J].合肥工业大学学报(自然科学版)，2009，32(5)：609-614.

[2]汪庆年，李红艳，史凤娟，等.基于频谱分析的电机噪声源的识别[J].声学技术，2009，28(4)：529-531.

[3]张承宁，王再宙，宋强.基于传声器阵列电动汽车用电机系统噪声源识别研究[J].中国电机工程学报，2008，28(30)：109-112.

[4]李辉，徐艮，杨超，等.天窗电机噪声测试及特征频率提取方法[J].中国电机工程学报，2011，31(18)：87-92.

[5]刘敏，董大伟，闫兵，等.车用交流发电机噪声特性及噪声源测试分析[J].重庆理工大学学报(自然科学版)，2010，24(6)：13-17.

[6]王天利，张相坤，杨亮.用阶次分析法识别起动机的异响噪声[J].噪声与振动控，2014，34(1)：169-172.

[7]GUO WEI,TSE PETER W.A novel signal compression method based on optimal ensemble empirical mode decomposition for bearing vibration signals[J].Journal of Sound and Vibration,2013,332(2):423-441.

[8]HYVÄRINEN A.Fast and Robust fixed-point algorithms for independent component analysis[J].IEEE Trans on Neural Networks,1999,10(3):626-634.

[9]HYVÄRINEN A,KARHUNEN J,OJA E.Independent component analysis[M].New York:Wiley,2011.

Noise Source Identification of Vehicle’s Starting Motors Based on EEMD-Fast ICA-STFTApproach

GONG Cheng-qi,HUA Chun-rong
（School of Mechanical Engineering,South West Jiaotong University,Chengdu 610031,China）

A noise source identification method based on the ensemble empirical mode decomposition(EEMD),fast independent component analysis(Fast ICA)and short time Fourier transform(STFT)algorithms is proposed to study the noise source identification of vehicle’s starting motors.First of all,the EEMD algorithm is used to decompose the single channel noise of the starting motors into several intrinsic mode functions.Then,the Fast ICA algorithm is used to extract the independent components.Finally,using the better time-frequency characteristics of STFT algorithm,the time-frequency characteristics of the Fast ICA results are analyzed.Combining the results with the prior knowledge of the motor noise,the relationship between the independent components and the different noise sources of the motors is determined.

acoustics;noise source of motors;ensemble empirical mode decomposition(EEMD);fast independent component analysis(Fast ICA);short time Fourier transform(STFT)

TM331

A

10.3969/j.issn.1006-1355.2017.05.020

1006-1355(2017)05-0092-05+114

2017-03-16

国家自然科学基金资助项目（51405399）

龚承启（1991－）男，湖北省十堰市人，硕士研究生，主要研究方向为汽车振动与噪声控制。

华春蓉，女，研究生导师。

E-mail:hcrong@swjtu.cn