基于差分隐私保护的DPk-medoids聚类算法

高 瑜，田 丰，吴振强

(1.现代教学技术教育部重点实验室，陕西 西安 710062; 2.陕西师范大学 计算机科学学院，陕西 西安 710062)

基于差分隐私保护的DPk-medoids聚类算法

高 瑜1,2，田 丰2，吴振强1,2

(1.现代教学技术教育部重点实验室，陕西 西安 710062; 2.陕西师范大学 计算机科学学院，陕西 西安 710062)

聚类分析是数据挖掘中的一个重要研究领域，由于聚类分析能够发现数据的内在结构并对数据进行更深入的分析或预处理，因此被用于图像处理、模式识别等诸多领域中。若用户数据被一些持有大数据集的组织(如医疗机构)利用挖掘工具获取个人隐私，将可能导致用户敏感信息面临泄露的威胁。为此，结合差分隐私的特性，提出了一种基于差分隐私保护的DPk-medoids聚类算法。该算法在每次发布真实中心点之前使用拉普拉斯机制对中心点加噪，再发布加噪之后的中心点，在一定程度上保证了个人隐私的安全性，以及聚类的有效性。真实数据集上的仿真实验结果表明，提出的聚类算法可以适应规模、维数不同的数据集，当隐私预算达到一定值时，DPk-medoids聚类算法与原始聚类算法的有效性比率范围可达0.9～1之间。

数据挖掘；隐私保护；差分隐私；k-中心性聚类

1 概 述

数据挖掘中的聚类分析已经广泛地应用于许多领域，如在Web搜索中由于Web页面数量巨大，通常是把关键词搜索返回的大量结果通过聚类算法进行分组，以简洁的方式呈现给用户。而数据挖掘的对象是存在拥有大量数据的多个组织(如社交网络、医疗机构、人口普查等)，这样的组织通常都会存储大量的用户敏感信息，在进行数据挖掘时就会引发用户隐私泄露的问题。该问题可以分为两方面：一方面，有些信息是在无意识下收集的，比如在汽车保险行业中，通过聚类算法会发现索赔率较高的客户群，如果这些信息泄露，就会使得保险业增加索赔率较高用户的保险金额；另一方面，各种数据挖掘方法与工具的不断完善，为一些用户提供便捷的手段来获取他人信息，比如人肉搜索等。

因此需要在隐私保护的前提下进行数据挖掘操作，不仅需要保护数据中的敏感属性，而且还要将隐私保护方法对挖掘结果的影响程度控制在一定范围之内[1]。

隐私保护的数据挖掘方法主要考虑数据的分布方式、数据的修改、隐私保护的对象和隐私保护技术几个方面[2]。传统隐私保护技术大多基于k-匿名保护模型，这种方法需要特殊的攻击假设，对k-匿名保护模型而言，后期总会出现一些新型的攻击方式。比如链接攻击，攻击者若能拿到两份数据表，且两份数据表具有相同的一条属性，那么攻击者就可以通过连接数据表推测出用户的敏感信息。2000年，Yehuda Lindell等[3]提出了隐私保护下的数据挖掘问题，利用ID3算法及其扩展处理干扰后的噪音数据，使其尽可能保持了分类的结果。

2002年，L. Sweeney等[4]提出基于传统隐私保护k-匿名模式下的数据挖掘算法，利用其中一条记录与其他k-1条记录的不可区分性实现隐私保护。2006年，Dework等提出了一种新型的隐私保护模型—差分隐私保护[5-7]方法。该方法不需要关心攻击者的背景知识假设和具有严格的数学定义及隐私证明等优点广受研究者的欢迎，通过对分析结果添加噪音，从而进行扰动，达到隐私保护的效果。差分隐私下的数据挖掘也得到了部分研究者的重视，通过对数据挖掘中已有算法进行调整和对数据挖掘结果的性能评估，找出数据安全性和模型可用性的平衡[8]。

Avrim Blum等[9]基于SuLQ框架设计了一个差分隐私k-means聚类算法，只需发布每次更新平均值的近似值就不会泄露隐私，整个过程是满足差分隐私条件。2011年，Dework针对文献[9]提出了改进算法[10]，主要是隐私预算的分配发生变化。李杨等[1]对Dework提出的IDP-kmeans理论进行验证，仿真实验表明，改进后的IDP-kmeans算法比DP-kmeans算法的聚类效果更优，并且实现了对大数据集加入少量隐私预算，达到高隐私保护的目的。Su Dong等[11]提出了实现k-means聚类的非交互式方法的EUGkM算法以及DPLloyd的改进算法。吴伟民等[12]提出了基于差分隐私的DBScan聚类算法，该算法在添加少量的随机噪音下，能够得到隐私保护并且保持聚类的有效性。

基于差分隐私保护的k-means聚类方法中，没有考虑到离群点对聚类的影响。为此，提出了基于差分隐私保护的k-medoids聚类算法，以解决离群点带来的敏感性问题。该算法通过加入拉普拉斯噪音，实现了对敏感数据的隐私保护。

为验证该算法的有效性和可行性，对该算法进行了可行性证明和仿真实验。安全分析和模拟实验结果均表明，该算法在引入差分隐私保护后可实现数据的可用性和安全性，且不同规模的数据集具有不同的有效性。

2 DPk-medoids算法描述与算法分析

2.1差分隐私的相关定义

即使攻击者知道某一个数据集除一条记录之外的其他所有信息，差分隐私保护模型也能保证攻击者不会通过剩余的这一条记录从输出结果中获得额外信息。所关注的焦点是在聚类过程中如何使得距离公布时的隐私不被泄露。当提交聚类模式查询时，返回的是经过差分隐私处理后的结果。

定义1[13](差分隐私)：给定相差一条记录的相邻两个数据集D1和D2，Range(A)是隐私挖掘算法A的取值范围，如果算法A的任意可能输出结果S(S∈Range(A))满足式(1)，算法A满足ε-差分隐私。

Pr[A(D1)∈S]≤exp(ε)×Pr[A(D2)∈S]

(1)

其中，相邻两个数据集D1和D2是指|D1ΔD2|=1，|D1ΔD2|表示D1ΔD2中记录的数量。

差分隐私保护主要是通过添加噪音机制技术来实现，适用于数值类型数据是拉普拉斯机制，噪音添加过多，数据真实性降低，噪音添加过小，隐私保护水平降低，所以添加噪音量的大小对数据可用性及隐私保护程度有不同的影响。敏感度是决定噪音大小的关键参数，当ε保持不变的情况下，敏感度越大，添加的噪音量越大。

定义2[6](敏感度)：设有函数f:D→Rd(R表示映射的实数空间；d表示查询维度)，对于任意的相邻数据集D1和D2，全局敏感度为：

(2)

文献[6]提出的拉普拉斯机制满足差分隐私，该机制是利用双指数分布产生的噪音，实现了隐私保护，而噪音是从位置参数为0，尺度参数为b的拉普拉斯概率密度函数Pr[η=x]=(1/2b)e-|x|/b中计算得到。

定义3[14](拉普拉斯机制)：给定数据集D，设有函数f:D→Rd，敏感度为Δf，设A是基于拉普拉斯机制的隐私挖掘算法，那么算法A(D)=f(D)+〈Lap1(Δf/ε),…,Lapd(Δf/ε)〉提供差分隐私保护。

设A是基于拉普拉斯机制的聚类算法，S为算法A输出的噪音结果，则S近似服从方差为Δf/ε、期望为0的拉普拉斯分布：

(3)

其中，f(D)表示真实聚类算法的计数查询。

2.2评价指标

定义4：聚类有效性评价指标DB。

(4)

2.3DPk-medoids算法

以汽车保险行业为例，通过聚类算法会发现索赔率较高的客户群，如果这些信息泄露，就会使得保险业增加索赔率较高用户的保险金额。聚类分析的主要研究任务是基于距离的聚类，因此在计算离每个中心点最近的点会泄露隐私，通过添加随机噪音发布一个近似中心点的值，攻击者就无法利用已有的背景知识推断出索赔率较高的客户群的隐私。

参数表示如表1所示。

表1 参数表示

详细描述如下：

算法1：DPk-medoids算法。

输入：k,D={x1,x2,…,xn},xi∈Rd,1≤i≤n；

输出：k个簇S1,S2,…,Sk。

1.flag=True;count=0;Min=Maxdis //Maxdis为距离的上界

3.While flag

4.Fori=1∶n

5.Forj=1∶k

8.m=j;

9.End if

10.End for

11.Sm=Sm∪xi//将xi分配给距离最近的中心点，并形成k个簇

12.End for

13.Forj=1∶m

14.Fori=1∶n

17.End if

21.Else

22.count++;

23.End if

24.End for

25.If count≥(n-k)·k//E为非负的个数

26.flag=false;

27.End if

28.End for

29.End while

设D1、D2是相差一条记录的两个数据集，在分配到簇时，可以看作是有k个桶的直方图查询，因此在d维空间[0,1]d上添加或者删除某个样本点，每个维度的最大变化是1，那么整个查询敏感度为d。令S1和S2分别为算法DPk-medoids在相邻数据集D1、D2上的输出结果，S是任意一种聚类划分，根据式(1)～(3)可得：

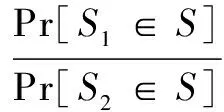
exp(ε)

(5)

其中，c(x)表示加噪后的聚类查询结果；r(D1,x)和r(D2,x)分别表示在数据集D1和D2的真实聚类查询。

由式(5)可知，DPk-medoids满足ε-差分隐私。

3 实 验

通过具体的数据实验对DPk-medoids算法的可用性进行分析和说明。实验环境为Inter(R)Xeon(R) CPU E5 1650V3@3.5 GHz，32 GB内存，Windows7 64位操作系统，实验使用Matlab2013实现DPk-medoids。算法中用到的数据全部来源于UCI Knowledge Discovery Archive database，具体信息如表2所示。

表2 数据信息

研究的主要目的是保证挖掘过程不会泄露隐私，DPk-medoids聚类算法中隐私预算ε越小，加入的噪音越大，保护程度越好。

3.1实验结果图

实验对数据集进行归一化预处理，使得各个属性值控制在[0,1]范围内。对数据集分别运用k-medoids和DPk-medoids，并做出两种算法的DB比率曲线图。其中，对于每个ε值，由于添加噪音的随机性，所以在不同数据集上调用DPk-medoids算法30次后取DB值的平均值。如果DB比率越接近1，那么两种算法聚类后的有效性就越接近，结果如图1～3所示。

图1 DS1的DB指标图

图2 DS2的DB指标图

3.2结果分析

从实验结果可知，DPk-medoids算法在一定程度上保证了个人隐私不会被泄露，同时也保证了聚类的有效性，它不会因为添加拉普拉斯噪音而受到巨大影响。图1中当ε为5时，添加噪音的聚类的有效性开始稳定，并且从纵坐标的含义可知，得到差分隐私保护后的聚类与原始聚类的有效性基本相同。

由图1～3可知，数据集越大，需要的ε越小，说明大数据集需要在较高的隐私保护级别下取得更好的效用性。因为添加敏感度为d的拉普拉斯机制时，决定噪音的参数是数据集的维数，所以加入噪音量的多少与数据集的大小没有关系。对比图2、3可知，在相同的隐私保护下，高维数据集的有效性低于低维数据集的有效性；对比图1、3可知，小数据集聚类可用性低于大数据集。

图3 DS3的DB指标图

4 结束语

隐私保护数据挖掘旨在保证数据的安全性和有效性。差分隐私能够提供很强的隐私证明来达到隐私保护的效果。为此，结合拉普拉斯机制，提出了一种满足ε-差分隐私保护的聚类算法DPk-medoids。理论证明，加入拉普拉斯过程能够满足差分隐私。而仿真实验结果表明，在引入差分隐私保护后可实现可用性和安全性的平衡，且不同规模的数据集有不同的有效性。此外，因噪音添加的大小直接影响聚类结果和隐私保护程度，所以在实现隐私保护的同时又能实现与原始聚类相同的有效性，将是未来的研究方向之一。

[1] 李 杨,郝志峰,温 雯,等.差分隐私保护k-means聚类方法研究[J].计算机科学,2013,40(3):287-290.

[2] 雷红艳,邹汉斌.限制隐私泄露的隐私保护聚类算法[J].计算机工程与设计,2010,31(7):1444-1446.

[3] Lindell Y,Pinkas B.Privacy preserving data mining[C]//International cryptology conference on advances in cryptology.[s.l.]:[s.n.],2000:36-54.

[4] Sweeney L.K-anonymity:a model for protecting privacy[J].International Journal on Uncertainty,Fuzziness and Knowledge-based Systems,2002,10(5):557-570.

[5] Dwork C. Differential privacy[C]//Proceedings of the 33rd international colloquium on automata,languages and programming.Venice,Italy:[s.n.],2006:1-12.

[6] Dwork C.Differential privacy:a survey of results[C]//International conference on theory & applications of models of computation.[s.l.]:[s.n.],2008:1-19.

[7] Dework C, Lei J. Differential privacy and robust statistics[C]//ACM symposium on theory of computing.[s.l.]:ACM,2009:371-380.

[8] 熊 平,朱天清,王晓峰.差分隐私保护及其应用[J].计算机学报,2014,37(1):101-122.

[9] Blum A,Dework C,Mcsherry F,et al. Practical privacy:the SuLQ framework[C]//Twenty-fourth ACM Sigact-Sigmod-Sigart symposium on principles of database systems.[s.l.]:ACM,2005:128-138.

[10] Dework C.A firm foundation for private data analysis[J].Communications of the ACM,2011,54(1):86-95.

[11] Su D,Cao J,Li N,et al.Differentially private K-Means clustering[C]//Conference on data and application security and privacy.[s.l.]:ACM,2015.

[12] 吴伟民,黄焕坤.基于差分隐私保护的DP-DBScan聚类算法研究[J].计算机工程与科学,2015,37(4):830-834.

[13] 张啸剑,王 淼,孟小峰.差分隐私保护下一种精确挖掘top-k频繁模式方法[J].计算机研究与发展,2014,51(1):104-114.

[14] Dwork C,McSherry F,Nissim K,et al.Calibrating noise to sensitivity in private data analysis[C]//Theory of cryptography conference.[s.l.]:[s.n.],2006:265-284.

[15] Davies D L,Bouldin D W.A cluster separation measure[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1979,1(2):224-227.

ADPk-medoidsClusteringAlgorithmwithDifferentialPrivacyProtection

GAO Yu1,2，TIAN Feng2，WU Zhen-qiang1,2

(1.Key Laboratory of Modern Teaching Technology of Ministry of Education,Xi’an 710062,China; 2.School of Computer Science,Shaanxi Normal University,Xi’an 710062,China)

Cluster analysis is one of the significant research fields in the data mining.Due to its paramount advantages in identification of the internal data structure and pretreatment/analysis of the data,it can be used in fields of the image processing and pattern recognition and so on.Users’ sensitive information could face leaking threats if mining tools are used to obtain the personal privacy by some organizations which own large datasets,such as medical companies.Therefore,taken into the characteristic of differential privacy account,a DPk-medoids algorithm based on differential privacy protection is proposed.It releases the noised center points before using Laplace mechanism to add noise,and in certain degree,personal privacy security and the effectiveness of clustering can be ensured.Experimental results with the ture datasets show that it can be applied to datasets with different scales and dimensions and moreover the range of effective ratio can reach to 0.9～1 compared with original clustering algorithm when the privacy budget reaches a certain value.

data mining;privacy preserving;differential privacy;k-medoids clustering

TP309.2

A

1673-629X(2017)10-0117-04

2016-10-01

2017-02-15 < class="emphasis_bold">网络出版时间

时间：2017-07-11

国家自然科学基金资助项目(61602290，61173190)；中央高校基本科研业务费(GK201501008，GK261001236)

高 瑜(1990-)，女，硕士研究生，研究方向为差分隐私保护；吴振强，教授，博士生导师，研究方向为隐私保护、分子通信。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170711.1454.036.html

10.3969/j.issn.1673-629X.2017.10.025