基于标准误差的最小二乘线性分类器
王刚刚,赵礼峰,谢亚利
(1.南京邮电大学 理学院,江苏 南京 210003;2.上海师范大学 数理学院,上海 200234)
基于标准误差的最小二乘线性分类器
王刚刚1,赵礼峰1,谢亚利2
(1.南京邮电大学 理学院,江苏 南京 210003;2.上海师范大学 数理学院,上海 200234)
大数据时代下数据结构的多样性严重影响人们对数据分类的判断。有效解决数据分类问题并提高分类准确率是大数据时代背景下亟待解决的难题。分类问题是将数据按照某种特征进行划分,并根据分类结果的准确性来判断分类特征的优劣。现有的模式识别中处理无监督分类问题的方法都有着自身固有缺陷。人为主观选择分类特征会降低模型的拟合效果。为此,提出一种将标准误差作为分类特征的线性分类器。该分类器在对样本进行分类的过程中,可保证分类的标准误差最小,从而保证了模型最终分类结果的准确性最高。基于该分类器进行了建模仿真验证。仿真实验结果表明,该分类器对样本分类的标准误差较小,准确率较高且复杂度也相对较低。相对于其他线性分类器,该分类器具有高效性和实效性的优势。
K-means聚类分析;最小二乘法;标准误差;分类器
0 引 言
分类问题是大数据时代一个重要的组成部分,分类在各行各业都有广泛的应用,比如超市商品的分配摆放、文本数据的情感分析、微博数据的网络图模形等都需要利用分类方法来处理。分类方法可分为监督分类法和无监督分类法。各行业中的数据大多数属于无监督分类数据。徐鹏等采用C4.5决策树的流量分类方法完成对未知网络流样本的分类[1];张建萍等以儿童生长发育时期的数据为例,通过聚类分析软件和改进的K-means算法来阐述聚类分析在数据挖掘中的实践应用[2]。这些案例都是利用没有预先分类的数据对数据进行挖掘探索,进行有效分析并产生了良好的效果。在对数据进行分类时,需要选取特定的指标。张高胤等采用K近邻分类算法,以距离为分类依据,对搜索到的网页进行主题分类[3];平源采用支持向量机聚类算法,对具有任意形状或不规则的数据集进行划分处理[4];张婷等在使用ISODATA算法时,设计了一种自适应参数确定算法,降低了图像关键点特征维数并缩短了检索时间[5]。
常用的处理无监督数据的分类方法有K-means聚类分析、ISODATA集群算法和CLARANS算法。K-means聚类分析[6]是MacQueen提出的一种聚类算法,该算法以距离为分类指标对数据进行分类;ISODATA集群算法[7]是J. C. Dunn提出的应用模糊数学判据的算法,该算法通过不断修改聚类中心的位置来进行分类;Raymond T. Ng提出了CLARANS算法[8],它是分割方法中基于随机搜索的大型应用聚类算法。这些经典分类法[6-8]都有一定的局限性,统计指标的选取比较主观,没有考虑如何在分类过程中减小分类误差。
现有文献都是阐述如何选取特定的统计指标以及相应的分类方法对样本进行分类,而没有阐述如何在分类过程中控制分类误差,对于无监督数据的分类,无法从分类结果计算分类准确性,同时不同分类指标的选取也会影响分类结果的准确性,导致无法了解分类的效果,因此只有在分类过程中降低样本分类的错判率才能提高分类结果的准确性。为此,提出了一种将标准误差作为分类特征的最小二乘线性分类器,在分类过程中对分类样本数据的误差进行控制并保证样本分类的标准误差最小。
1 基础知识
1.1K-means聚类分析
K-means算法以空间中k个点为中心进行聚类,对最靠近它们的对象进行归类[9]。
算法流程如下:
(1)从n个样本点中任意选择k个对象作为初始聚类中心;
(2)对于剩下的样本点,根据它们与这些聚类中心的距离,分别将它们分配给与其最相似的聚类中心所在的类别;
(3)计算每个新类的聚类中心;
(4)不断重复步骤2和步骤3,直到所有样本点的分类不再改变或类中心不再改变为止。
1.2最小二乘估计模型
最小二乘法通过最小化误差平方和寻找数据的最佳函数匹配,使得实际数据与预测数据之间的误差平方和最小。
多元线性回归模型的一般形式为:
y=β0+β1x1+…+βpxp+ε
(1)
其中,β0,β1,…,βp为p+1个未知参数,β0称为回归参数,β1,…,βp称为回归系数;y为因变量;x1,x2,…,xp为自变量;ε为随机误差
当p≥2时称式(1)为多元线性回归模型。对于多元线性回归模型,若获得n组可观测样本xi1,xi2,…,xip,yi,则多元线性模型可表示为[10]:
yi=β0+β1xi1+…+βpxip+εi,i=1,2,…,n
(2)
拟合后的多元线性回归模型的一般形式为:
(3)

多元线性回归方程的标准误差为:
(4)

2 最小二乘线性分类器的构造
2.1构造思想
最小二乘线性分类器通过构造若干个最小二乘线性回归方程,计算出各个方程的标准误差,以标准误差为分类依据将数据划分为若干类。
首先利用样本数据拟合一条多元线性回归方程,然后采用K-means聚类分析法将数据分为k类,并拟合得到k个最小二乘线性方程,有效地降低了样本数据拟合的标准误差。然后对k个最小二乘线性方程进行归一化处理,即赋予每一个线性回归方程一定的权重,归一化线性方程为每个线性方程的加权和。因此可以计算归一化线性方程的标准误差和以总样本数据拟合的线性方程的标准误差,比较两者所得到的标准误差大小,以此对样本进行分类,标准误差较小的样本数据可划分到对应的线性方程那一类。
上述两条线性方程至多只能将数据分为三类:{样本点离归一化线性方程较近},{样本点离以总样本数据拟合的线性方程较近},{样本与两线性方程距离相等},显然不满足类别较多的需求。当样本属性类别较多时,可将由k类线性方程得到的标准误差进行排序,根据顺序对k类线性方程分组,对每组内的线性方程进行归一化处理,得到若干个归一化的线性回归方程。以标准误差为分类指标对样本进行分类。
针对样本较多,计算量较大的情况,利用K-means聚类分析法,通过比较类间标准误差的大小对样本进行分类。新分类器在对样本数据处理的过程中,以标准误差为分类依据,保证了每一类样本数据误差最小;对数据进行聚类分析处理,类标准误差相对总体标准误差变小了,同时也减少了数据分类的计算量。
2.2构造流程
数据特征的选取决定数据的分类情况,数据分类模型的准确性是评判模型优劣的重要标准。提出了一种将标准误差作为分类特征的线性分类器,该分类器保证模型分类结果的标准误差最小,即保证模型分类结果的错判率最低。
最小二乘线性分类器的具体构造流程如下:
(1)利用总体样本数据,拟合线性回归方程;
(2)对总体样本数据进行K-means聚类处理,并对每一类(k类)样本进行线性回归方程的拟合;
(3)在对k个线性回归方程归一化处理之前,设定每一类(k类)线性方程的权重;
(4)对k类线性回归方程进行归一化处理;
(5)计算步骤1~4得出的线性方程,拟合步骤2中k类样本数据所得到的预测值与真实值之间的标准误差;
(6)根据步骤5所得到的标准误差对数据进行分类。
2.2.1 线性回归方程的拟合

采用K-means聚类分析法对该样本数据进行分析,将数据分为k类[11]。假设k类样本数据量分别为n1,n2,…,nk。利用k类样本数据,采用最小二乘法拟合得到k个线性回归方程:
(5)
k个线性回归方程权重的设定:将第k类数据带入第m个线性回归方程,得到预测值,计算其与真实值间的标准误差,结果如表1所示。

表1 标准误差
计算表1内所有标准误差值之和,记为总标准误差;计算第k行除去对角线上元素的标准误差之和,记为类间拟合误差。类间拟合误差越小,表明第m类线性方程拟合的效果越好,设定的权重就越高,该权重值等于总标准误差减去类间拟合误差的值与总标准误差之比,取αm表示第m类线性回归方程的权重。

m=1,2,…,k
(6)

(7)
(8)
2.2.2 分类特征的选取与计算

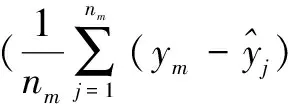
(9)


(10)


(11)
2.2.3 标准误差的比较与分类器的建立
对比ERRORm与Errorm的关系,其大小即为所设计的最小二乘线性分类器对样本进行分类的依据。ERRORm和Errorm至多存在3种关系,即Errorm>ERRORm,Errorm 3.1实值仿真 利用R语言编程环境实现算法,选取联合循环发电厂数据集进行仿真实验[12]。该数据集包含了9 568个数据点以及5个属性特征,分别是温度(AT)、排气真空(V)、环境压(AP)、相对湿度(RH)和网每小时输出的电能(EP)。分别以x1,x2,x3,x4替代前四个属性变量,作为解释变量;y替代网每小时输出的电能,作为被解释变量。 首先对该数据集进行相关性检验,发现该数据集满足最小二乘的假设条件。利用R软件对该数据集作拟合处理,得出线性回归方程: 0.233 916x2-0.062 083x3-0.158 054x4 (12) 采用K-means聚类分析法对该数据集进行分类,通过对数据集的观测以及资料阅读[13],发现将该数据集化为4类较佳,利用R软件采用K-means聚类分析4类数据[14],每一类数据集详情如表2所示。 表2 分类数据样本 分别对这4类样本采用最小二乘法作线性回归处理,得到线性回归模型如下: 0.240 20x3-0.145 43x4 0.082 47x3-0.171 64x4 0.279 35x3-0.079 06x4 0.071 87x3-0.204 59x4 (13) 表3 线性回归方程拟合误差 根据式(6)可确定4个线性回归方程的权重,如表4所示。 表4 权重值 重新构造的最小二乘估计线性回归方程为k个线性回归方程的加权之和: 1.580 130 3x1-0.173 724 4x2+ 0.143 711 4x3-0.147 273 8x4 (14) 通过未分类的线性回归方程和分类后归一化的线性回归方程,可计算分类样本的标准误差,结果如表5所示。 表5 分类样本的标准误差 利用R软件对算法进行编译并绘制分类样本的标准误差及差值图,如图1所示。 图1 标准误差及差值 因此该最小二乘线性分类器方程为: 0.062 083x3-0.158 054x4 (15) 联立上述线性回归方程即可得出两个超平面相交的部分。 根据图1可以看出,在设置标准误差阈值为0.1的条件下:分类1和分类3:ERROR>Error;分类2:ERROR=Error;分类4:ERROR 表6 分类器重新分类结果 3.2新分类器与经典分类器的比较 3.2.1 复杂度 处理一个样本数为n的数据集,利用K-means聚类分析法和ISODATA算法处理n个样本数,假设需要进行p次迭代,每个样本点需要操作m次,则其复杂度为O(pmn);利用CLARANS算法处理n个样本,其复杂度为O(n2);利用最小二乘线性分类器处理数据,假设对数据进行处理得到M条线性方程,复杂度为O(n),每个样本与M条线性方程的标准误差复杂度不超过O(Mn),其复杂度为O((M+1)n)。当M=3时,样本最多可分为7类,可以满足分类类别的需求;而p和m值不小于2,pm最小为9,因此最小二乘线性分类器的复杂度较低。 3.2.2 准确率 无监督数据分类结果无法判断分类的准确率,经查阅文献,根据最小二乘法的性质可知,采用最小二乘法得到的线性回归方程的估计误差最小[15]。新分类器在对无监督样本处理的过程中,以标准误差为分类依据,保证了每一类样本标准误差最小,即新分类器相比较经典分类器的准确率较高。 大数据的涌现使人们在处理复杂的数据对象时面临巨大的挑战。数据的多源异构、质量的良莠不齐使得传统的机器学习法不能有效地处理。对于模式识别中无监督数据的处理问题,单从主观性选取数据特征对数据做分类处理无法保证分类模型的准确度。因此立足于研究分析的目的,选择合适的量化指标才能有效地建立以数据为中心的分类模型。 现有的模式识别中处理分类问题的方法通常会选择样本均值、样本众数、样本中位数作为分类特征,并计算最终样本分类结果的错判率来判断该分类特征的优劣性,然而这种方法并不能保证样本分类结果的错判率最小,人为主观选择分类特征会降低模型的拟合效果。针对这一不足,提出了一种利用标准误差作为分类特征的线性分类器。分类模型的标准误差的大小反映了分类结果的错判率高低,保证分类模型中标准误差最小也就是保证样本分类模型的错判率最小,该方法可以高效地对样本进行分类。实验结果表明,该分类器得到的分类模型准确率较高。 [1] 徐 鹏,林 森.基于C4.5决策树的流量分类方法[J].软件学报,2009,20(10):2692-2704. [2] 张建萍,刘希玉.基于聚类分析的K-means算法研究及应用[J].计算机应用研究,2007,24(5):166-168. [3] 张高胤,谭成翔,汪海航.基于K-近邻算法的网页自动分类系统的研究及实现[J].计算机技术与发展,2007,17(1):21-23. [4] 平 源.基于支持向量机的聚类及文本分类研究[D].北京:北京邮电大学,2012. [5] 张 婷,戴 芳,郭文艳.基于ISODATA聚类的词汇树图像检索算法[J].计算机科学,2014,41(11A):123-127. [6] 李 飞,薛 彬,黄亚楼.初始中心优化的K-Means聚类算法[J].计算机科学,2002,29(7):94-96. [7] 钱夕元,邵志清.模糊ISODATA聚类分析算法的实现及其应用研究[J].计算机工程与应用,2004,40(15):70-71. [8] Ng R T,Han J.CLARANS:a method for clustering objects for spatial data mining[J].IEEE Transactions on Knowledge & Data Engineering,2002,14(5):1003-1016. [9] 黄 韬,刘胜辉,谭艳娜.基于k-means聚类算法的研究[J].计算机技术与发展,2011,21(7):54-57. [10] 高学军,王振友.多元统计回归模型在医疗保障基金数额分配中的应用[J].统计与决策,2009(9):145-146. [11] Everitt B.Cluster analysis[J].Quality & Quantity,1980,14(1):75-100. [12] Tufekci P,Kaya H.Combined cycle power plant data set[DB/OL].(2014-03-26)[2016-05-02].http://archive.ics.uci.edu/ml/datasets/Combined%20Cycle%20Power%20Plant. [13] 朱佳贤.无指导学习环境下基于属性相关性分析和聚类算法的属性选择问题研究[J].管理学报,2005,2(S):162-165. [14] German D M,Adams B,Hassan A E.The evolution of the R software ecosystem[C]//17th European conference on software maintenance and reengineering.[s.l.]:IEEE,2013:243-252. [15] 丁克良,沈云中,欧吉坤.整体最小二乘法直线拟合[J].辽宁工程技术大学学报:自然科学版,2010,29(1):44-47. ALeastSquareLinearClassifierwithStandardError WANG Gang-gang1,ZHAO Li-feng1,XIE Ya-li2 (1.School of Science,Nanjing University of Posts and Telecommunications,Nanjing 210003,China;2.College of Mathematics and Physics,Shanghai Normal University,Shanghai 200234,China) The diversity of the data structure in the era of big data can seriously affect the people’s judgment of the data classification,which will be an urgent difficulty to solve data classification effectively and improve the accuracy of classification under the background of big data.Classification is to classify the data according to some characteristics and to judge the merits of classification characteristics by the accuracy of the classification results.The methods dealing with unsupervised learning classification in existing pattern recognition have their own inherent defects.Artificial subjective selection of classification characteristics will reduce the model fitting effect.Therefore,a linear classifier is proposed that the standard error is used as the classification feature to classify the data.In the process of classifying samples,it can ensure the minimum standard error of the classification,thus ensuring the highest accuracy of the final classification results.The simulation shows that it has less standard error,higher accuracy and lower complexity.Compared with other linear classifiers,it has the advantages of high efficiency and effectiveness. K-means clustering analysis;least square method;standard error;classifier TP181 A 1673-629X(2017)10-0078-05 2016-09-21 2016-12-27 < class="emphasis_bold">网络出版时间 时间:2017-07-11 国家自然科学青年基金项目(61304169) 王刚刚(1992-),男,硕士研究生,研究方向为信息统计与数据挖掘;赵礼峰,教授,硕士研究生导师,研究方向为应用数学。 http://kns.cnki.net/kcms/detail/61.1450.TP.20170711.1454.030.html 10.3969/j.issn.1673-629X.2017.10.0173 实值仿真和比较





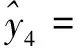









4 结束语

