基于特征融合的低倍镜下大鼠骨质疏松识别*

蔡洁，周珂，何文广，吴天秀，王龙

(1. 广东医科大学信息工程学院，湛江 524023；2. 广东医科大学基础医学院，湛江 524023)

1 引 言

近年来，研究者们对骨小梁的定量化研究越来越重视。纹理分析技术也越来越多的应用到X线、显微镜、Micro-CT、MRI等各种成像设备的图像分析工作中。杨新慧等人提取了骨X线图像骨小梁纹理分形特征分析，对10幅骨X线图像进行机器分类,分类结果表明了纹理分析方法有实用的潜在价值[1]。Karunanithi等人对绝经后妇女的根骨X线图像的骨小梁进行纹理分析，探讨了骨质疏松的成因问题[2]。Mallard等人对脊椎、桡骨远端和跟骨的X线图像进行了纹理分析，证明纹理分析方法可以在早期发现骨微观结构的变化，对于预防和治疗骨质疏松有实用价值[3]。Muthu Subash Kavitha等人对牙齿的X线图像进行了纹理分析，发现与传统指标结合可以有很好的辅助诊断作用[4]。嵇鸣等人对MRI图像提取了骨小梁的纹理参数，发现骨质疏松组(OVX组)和假手术组(SHAM组)的纹理存在着显著性差异[5]。

我们前期工作对显微镜下大鼠胫骨切片的骨小梁进行纹理分析，发现去卵巢组(OVX组)和假手术组(SHAM组)的骨小梁纹理存在显著性差异，并且对于4倍镜和10倍镜下的图像进行了分类识别，都达到了90%以上的识别率[6-8]。但是无论是4倍镜或者10倍镜，相较于2.5倍镜虽然能够得到更为清晰的纹理，均无法拍摄出完整的切片，需要靠人工定位来对一张切片拍摄出多组图片，无法保证骨小梁的形态完整性，在拍摄过程中也不可避免的会出现图片重叠或者缺漏的状况，同时还有光源变化的问题，这些都会对实验结果产生影响。2.5倍镜可以拍摄出完整的大鼠胫骨切片，但是由于图像分辨率低，仅仅依靠平常提取的纹理参数识别率低，因此，本研究分析了方向和距离对纹理参数的影响，对纹理参数进行了加权处理，并结合形状参数进行特征融合，对SHAM组和OVX组进行识别。希望这一研究为骨质疏松症的早期发现提供新的方法。

2 改进的骨小梁纹理参数提取

在图像中讨论骨小梁的微观结构的纹理结构是很重要的一个部分。本研究的纹理参数从灰度共生矩阵提取了11个纹理参数，从灰度游程矩阵中提取了4个参数，共提取了15个纹理参数。进行了t-检验后 ，挑选出具有显著性差异的纹理参数13个，分别是：灰度共生矩阵中提取的对比度、相关、方差、方差和、和均值、熵、和熵、差熵、差的方差、逆差矩；灰度游程矩阵中提取的游程长不均匀度、灰度不均匀度和短游程矩。

众所周知，利用灰度共生矩阵和灰度游程矩阵提取纹理参数时，要考虑4个方向：0°、45°、90°、135°，每个方向提取出相应的纹理参数，每个特征参数会有四组值。因此，特征参数值会受到所选取方向的影响。另外，灰度共生矩阵的纹理参数还有距离变化的影响。以往的研究中都是直接将四个方向做平均，即选择距离=1或者直接对所有距离做平均，未考虑各个方向纹理变化的作用以及距离的选择。由于低倍镜下的图像骨小梁内部像素点比较少，邻近像素点在灰度上的细微变化都会使共生矩阵产生不小的影响，因此，我们需要对提取的纹理参数做进一步的分析再来使用。

2.1 方向对纹理参数的影响分析

本研究在提取了纹理参数后，对两组样本在四个方向上的参数进行分析。

2.1.1方向对灰度共生矩阵纹理参数的影响 根据t-检验结果，灰度共生矩阵中选取了10个纹理参数：对比度、相关、方差、方差和、和均值、熵、和熵、差熵、差的方差和逆差矩。

对比度反映了图像的清晰度和纹理沟纹深浅的程度；相关度量灰度共生矩阵元素在各个方向上的相似程度，反映了纹理的方向性；熵表示了图像中纹理的非均匀程度或复杂程度；逆差距反映图像纹理的同质性，度量图像纹理局部变化的多少。这四个参数比较典型，因此，这里只选择对比度、相关、熵和逆差矩进行0°,45°,90°,135°四个方向数据做图比较，选取距离=3的数据绘图。见图1。

从图1中SHAM组和OVX组纹理参数的数值对比来看，SHAM组的对比度值较OVX组更大，说明SHAM组的纹理更加清晰；SHAM组的相关值较OVX组更大，说明SHAM组的纹理更加的均匀，同时，由于相关反映了纹理的方向性，我们发现，无论是SHAM组还是OVX组都在水平和垂直方向上表现出更为均匀的纹理特征，从高倍镜下的骨小梁纹理也可以看出这一点(见图2)；SHAM组的熵值较OVX组更大，说明SHAM组的图像信息量更大，纹理更加的复杂纹理更加的均匀；SHAM组的逆差矩值较OVX组更小，说明SHAM组的纹理更加富于变化，而OVX组的纹理局部变化比较少。这些数据都符合并且也从图像上直接反映出了骨质疏松后骨密度降低、骨结构模糊[9]这一基本事实，同时也说明通过对骨小梁图像的纹理分析进行骨质疏松的识别是切实可行的。

图1灰度共生矩阵纹理特征参数在不同方向上的值

(a)对比度；(b)相关；(c)熵；(d)逆差矩

Fig1TexturefeaturesofGray-levelCo-occurrenceMatrixinfourdifferentdirections

(a)contrast；(b)correlation；(c)entropy；(d) inverse difference moment

图2 SHAM组和OVX组骨小梁图像

另外，从图中各条曲线的变化情况来看，四个方向上的纹理特征参数值的变化规律基本相同，说明各方向上的纹理参数值对样本纹理都有正确的反应能力。对比度、熵和逆差矩在四个方向上的特征参数值差异都很小(其他6个参数也具有相同的规律)，但是相关对纹理参数在不同方向上的变化非常敏感，需要在最终的灰度共生矩阵纹理参数值计算中考虑这一因素。

2.1.2方向对灰度游程矩阵纹理参数的影响 根据t-检验结果，灰度游程矩阵选取了3个纹理参数：游程长不均匀度，灰度不均匀度，短游程矩。

游程长不均匀度描述图像中游程长度的相似性，如果整幅图像的游程长度较相似则游程长不均匀度的值越小，反之则越大；灰度不均匀度描述图像灰度值的相似度，如果整幅图像的灰度值较相似则灰度不均匀度的值越小，反之则越大；短游程矩描述短游程的分布情况，如果图像细纹理较多则短游程因子值较大，反之则越小。对这三个参数进行0°、45°、90°、135°四个方向数据做图比较，见图3。

从图3中SHAM组和OVX组纹理参数的数值对比来看，对于三个参数的数值，SHAM组都较OVX组更大，进一步说SHAM组相较于OVX组的纹理基元对比更强烈，纹理的复杂程度更高，整体图像的灰度值相似性更低，图像的细纹理更多更丰富，符合骨质疏松的图像特点。

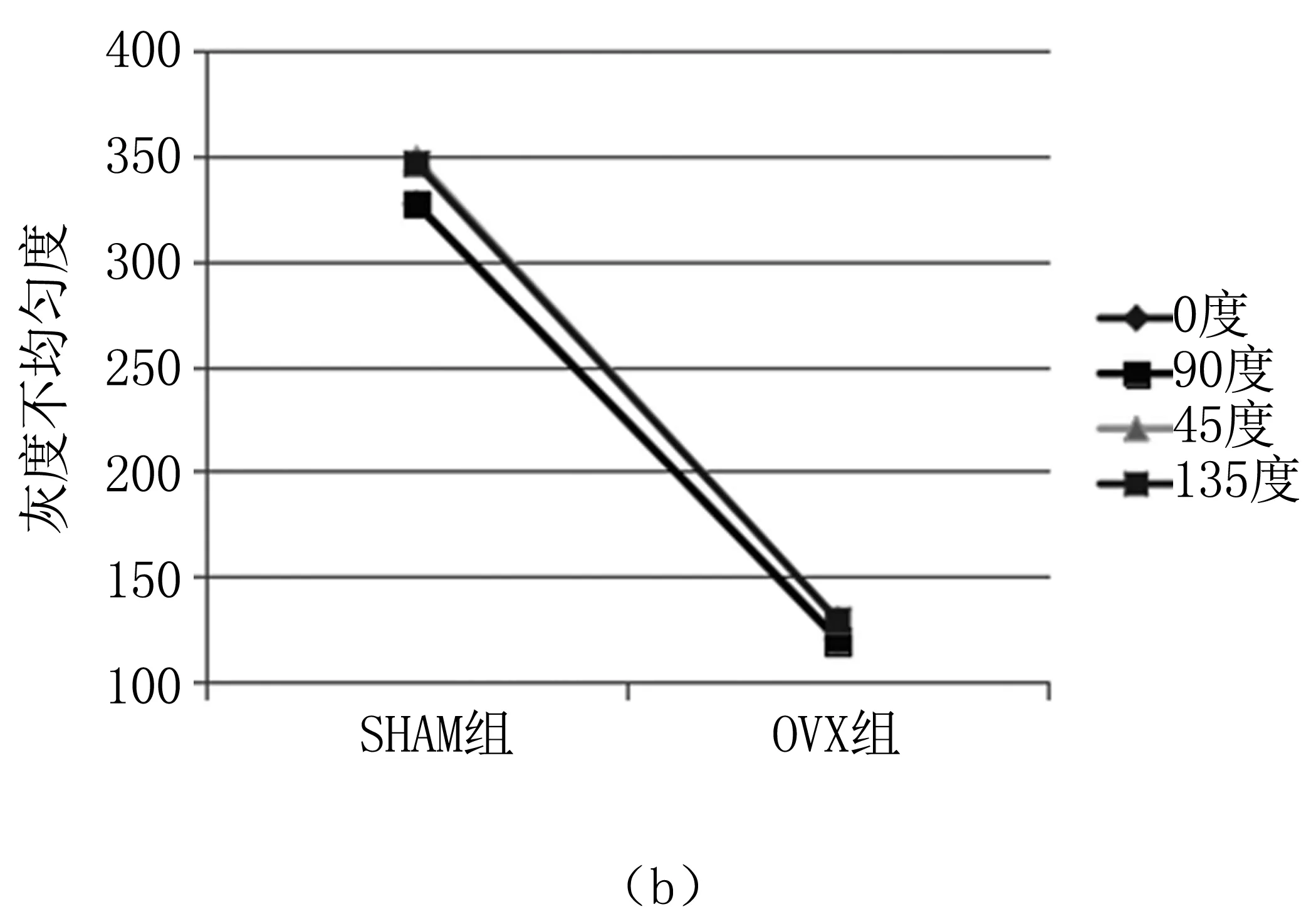
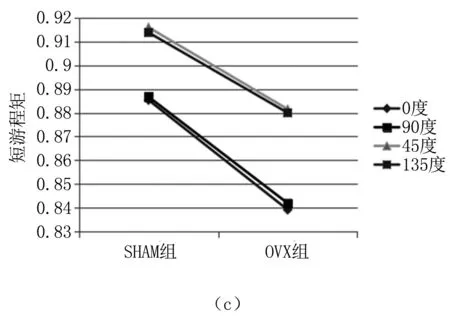
图3 灰度游程矩阵纹理特征参数在不同方向上的值

另外，从图中各条曲线的变化情况来看，四个方向上的纹理特征参数值的变化规律基本相同，说明灰度游程矩阵各方向上的纹理参数值对样本纹理也都有正确的反应能力。游程长不均匀度和灰度不均匀度在四个方向上的特征参数值差异很小，但是短游程矩对于方向的敏感度更高，我们需要在最终的灰度游程矩阵纹理参数值计算中考虑这一因素。

2.2 基于变异系数法的加权纹理参数计算

为了体现方向对纹理参数值的影响，需要给予各个方向参数不同的权重。变异系数法可以突出各方向的变化幅度，区别能力强，因此，我们采用变异系数法来进行加权系数的计算。在灰度共生矩阵的纹理参数中，相关对于方向具有最强的灵敏度，因此，用相关的值来进行加权系数的计算。算法描述如下：

假设x(i,1)，x(i, 2)，x(i, 3)，x(i,4)代表第i个样本图像在0°,45°,90°,135°方向上的相关值，则其均值为：

各个方向的变异系数为：

则各个方向的加权系数为：

按照此方法得到每一个样本四个方向的权重，假设p(i,j)(j=1,2,3,4)为第i个样本图像在各个方向的某一纹理参数值，那么最终计算出的样本i的此纹理参数值为：

同理，在灰度游程矩阵的纹理参数中，短游程矩对于方向具有最强的灵敏度，因此用短游程的值来进行加权系数的计算，过程如上所述。

2.3 距离对纹理参数的影响

考虑了方向对纹理参数的影响后，另外一个需要考虑的问题就是灰度共生矩阵的距离选取。前面说过由于低倍镜下的图像骨小梁内部像素点比较少，邻近像素点在灰度上的细微变化都会使共生矩阵产生不小的影响，因此，不同距离的选择对图像的分析结果有着显著的影响，需要选取合适的点对之间的距离，使实验效果达到最佳。

仍然以灰度共生矩阵的四个典型特征参数——对比度、相关、熵和逆差矩——来考虑参数值随着距离变化的情况，见图4。

图中显示了距离从1到5变化时纹理参数的变化情况。从图中可以看出，熵受距离的影响较小，对比度、相关和逆差矩都受距离影响相对较大。随着距离的增大，参数的变化逐渐变小，从图中可以看出四个参数的变化在距离等于3的时候都逐渐稳定(灰度共生矩阵的其余6个纹理参数也具有相同的变化规律)，当距离等于3时表现出了很好的鲁棒性，因此，在最终的灰度共生矩阵的纹理参数提取中，选择以距离等于3时进行加权计算。

3 形状参数的提取

2.5倍镜下纹理清晰度不高，仅靠纹理数据识别准确率低，但是2.5倍镜下可以拍摄出完整的大鼠胫骨切片，保证了骨小梁的完整性，同时形状也是骨小梁微细结构很重要的一种描述方式，因此，我们考虑提取骨小梁的形状特征，与纹理特征参数结合来进行识别，提高识别的准确率。对骨小梁形状的提取结果见图5。

图4灰度共生矩阵纹理特征参数在不同方向上的值

(a)对比度；(b)相关；(c)熵；(d)逆差矩

Fig4TexturefeaturesofGray-levelCo-occurrenceMatrixindifferentdistances

(a)contrast；(b)correlation；(c)entropy；(d) inverse difference moment

根据提取出的形状，计算了区域的一些形状参数，选择了4个有价值的无量纲的形状参数(t-检验结果存在显著差异)：

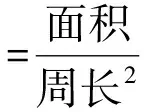
图5 骨小梁区域勾画

另外，本研究还提取了区域的7个Hu不变矩。这7个参数反应了图像区域的几何特征，并且具有旋转、平移、尺度等特性的不变特征，所以又称其为不变矩。在图像处理中，几何不变矩可以作为一个重要的特征来表示物体，可以据此特征来对图像进行分类等操作。

因此，本研究共提取了11个形状参数。

4 实验结果与分析

本实验共获取了52张有效的大鼠胫骨切片图像：其中SHAM组34张，OVX组18张。图像均拍摄于2.5倍显微镜下。

在之前的研究中发现，线性支持向量机(LSVM)方法的识别率更高，因此，本研究采用了LSVM分类方法、K-最近邻(KNN)分类算法和基于Fisher函数的线性判别分析方法(LDA)对两组样本进行分类识别，三种分类方法均基于留一交叉验证结果。

在三种分类方法下，分别讨论了未加权纹理参数(即直接对纹理参数做四个方向平均)、加权纹理参数(即用2.3的变异系数法对纹理参数进行加权)、未加权纹理和形状参数融合、加权纹理和形状参数融合四种情况下的识别准确率。见表1。

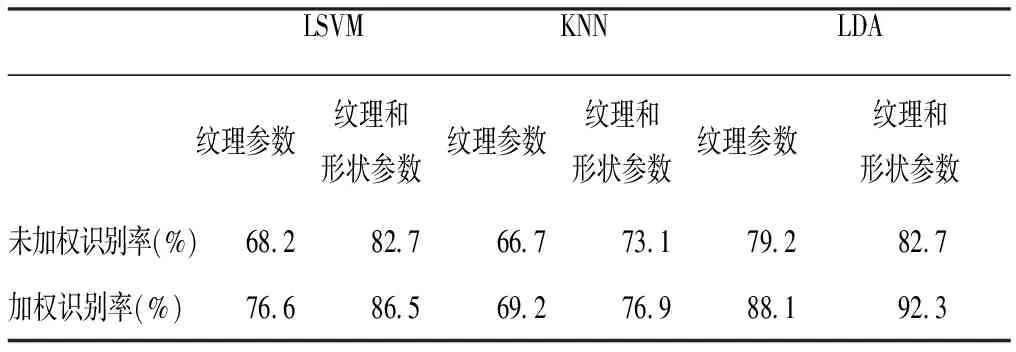
表1 三种分类器识别结果(%)

从表1中可以看出，经过本研究方法加权处理后的纹理参数识别率更高，同时将形状参数和纹理参数融合后识别率比仅用纹理参数的识别率更高。另外，从表中我们可以看出KNN分类算法这种依靠k-邻近点距离来进行分类识别的方法对于本研究并不理想，线性分类器更适用本研究的数据。

本研究的目的就是希望将研究结果用于临床诊断，因此根据诊断试验的评价指标，讨论了LSVM方法和LDA方法针对未加权纹理和形状参数融合、加权纹理和形状参数融合的两种情况计算了灵敏度和特异度这两个重要指标，结果见表2。

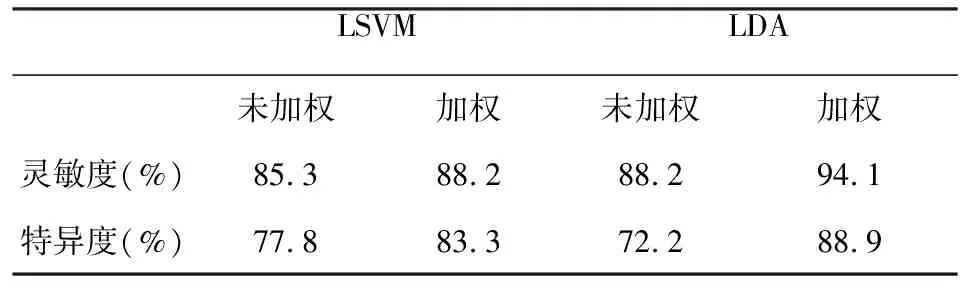
表2 灵敏度与特异度计算结果

从表2中可以看出，对纹理参数进行加权处理后的特异度明显提高，即误诊率得到了明显的降低，说明本研究的加权处理结果效果显著。

另外，我们针对加权纹理和形状参数融合的识别结果计算出约登指数(Youden’s index，YI)，可以得出：

线性SVM方法：YI=88.3%+83.3%-1=0.716 线性判别分析：YI=94.1%+88.9%-1=0.83

两种分类器得到的YI>0.7，说明本研究结果具有诊断应用价值。

5 结论

本研究将形状参数和纹理参数这两种不同模态下的图像特征参数结合，并考虑了方向和距离对纹理参数的影响，比常规方法有着明显的优势，具有很好的应用价值。下一步还需要深入研究的问题：(1)对图像的预处理工作进一步做到一致；(2)自动化分割，能够自动的区分边界实现自动分割；(3)研究结果(见表1、表2)发现LDA方法的识别率较LSVM方法更高，我们认为是由于特征参数之间存在相关性，而LDA方法可以将高维的模式样本投影到最佳鉴别矢量空间，使得LDA方法的识别率更高。因此，除了进行t-检验找出存在显著性差异的特征参数之外，根据参数的意义对特征参数进行降维筛选也是下一步研究中考虑的问题。