基于有限元分析的股骨干骨折内固定系统多因素的正交试验设计*

盛伟，纪爱敏△，陈长胜,2

(1. 河海大学机电工程学院，常州 213022；2. 常州奥斯迈医疗器械有限公司，常州 213022)

1 引 言

股骨干骨折是最常见的股骨损伤之一，通常由撞击、挤压等强大外力引起[1]。锁定钢板固定股骨干骨折的治疗效果得到了广泛的认可，但钢板或螺钉断裂率依然偏高[2]。为改变接骨板及螺钉频繁断裂的现状，国内外研究人员进行了大量的相关研究。Katthagen等[3]认为不同接骨板材料可改变锁定钢板的刚度和极限应力，而螺钉设计对其影响不大。张魁忠等[4]认为螺钉数目极大影响了内固定系统的结构稳定性，少螺钉固定可增加结构的弹性形变能力。Chen SH等[5]运用有限元方法对髓内钉和锁定钢板治疗股骨远端骨折的效果进行对比，但并未对内固定系统具体参数进行研究。张岩等[6]运用有限元方法探究单双皮质螺钉不同组合固定方式对内固定系统应力分布的影响，但其采用的全面试验法极大增加了试验次数，经济性与实用性较差。近年来，研究人员对锁定钢板螺钉布局的研究已经趋于成熟，根据林振恩等[7]研究得出的锁定钢板螺钉布局原则，本研究确定了股骨干骨折内固定系统的锁定钢板结构参数及螺钉布局方案。由于在股骨骨折处填充相对股骨较软的材料更能保证内固定系统的稳定性，本研究选取了锁定钢板固定股骨干骨折内固定系统中的螺钉直径、锁定钢板与股骨表面间距及股骨骨折处填充物弹性模量等对系统稳定性影响较大的系统因素，对此三个系统因素进行生物力学综合试验研究。在进行多因素的试验设计时，利用正交试验设计方法挑选出具有代表性的试验点进行试验，通过对正交试验结果的分析来全面了解试验的情况，极大的减少试验次数，且能选出多因素的最佳匹配方案[8]。因而，本研究提出基于三维建模技术及有限元分析方法，利用正交试验设计方法对锁定钢板固定股骨干骨折内固定系统的多个因素同步进行生物力学研究，并结合权矩阵分析方法计算出影响内固定稳定性的各因素各水平的权重，快速探究相应影响因素的主次次序与最佳匹配方案，为股骨干骨折内固定临床治疗提供指导。

2 试验方案设计

本研究主要对股骨干内固定系统的多个因素综合考虑，得到最佳的因素水平匹配方案，以保证内固定系统的稳定性。其中，主要研究的因素有螺钉直径A、锁定钢板与股骨表面间距B及股骨骨折处填充物弹性模量C等，每个因素各有三个水平，具体数据见表1。本研究为三因素三水平试验，通过正交表进行正交试验设计，三因素三水平正交表见表2。针对正交试验结果需要进行直观分析，如果经过计算得到的结果为Δ2>Δ3>Δ1，则说明因素B对该指标影响最大, 其次为因素C, 而因素A影响最小[9]。本研究试验结果有三项指标：植入物最大等效应力、股骨干最大等效应力和内固定系统最大轴向位移，指标均越小越好。

表1因素与水平表

Table 1 The table of factors and levels

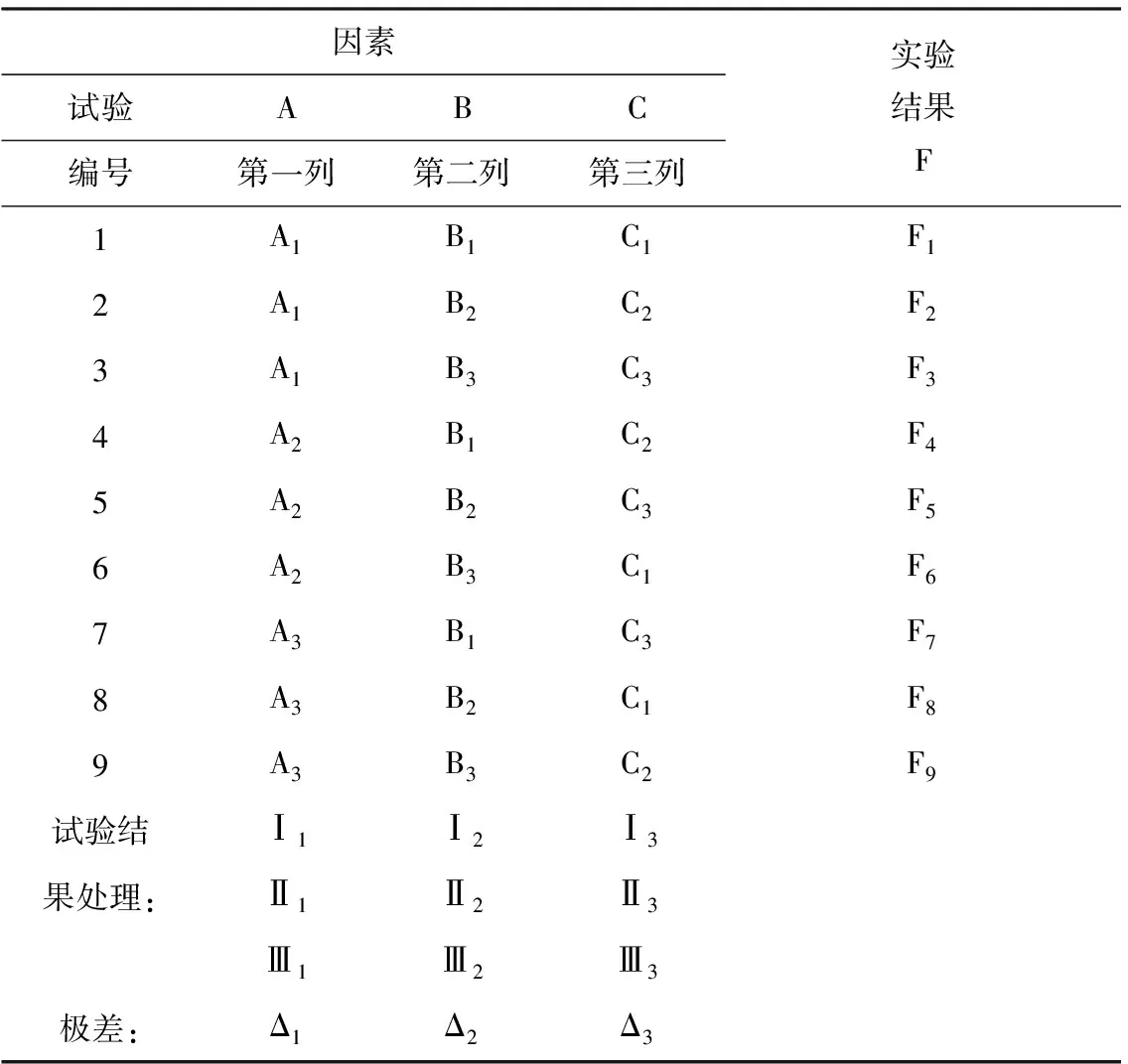
表2 三因素三水平正交表Table 2 Three factors and three levels orthogonal table

3 有限元模型的建立与求解

3.1 几何模型简化

由于股骨近端和股骨远端结构对股骨干骨折受力影响不大，又由于股骨干形状形似圆柱体且骨干髓腔为中空，故在三维建模软件Pro/E中建立股骨模型时，去除复杂的股骨近端和股骨远端，用中空圆柱来代替股骨干。假定骨干部分不存在松质骨，设置皮质骨为整个股骨干模型的材料属性[10]。同时，简化接骨螺钉为圆柱体，简化锁定钢板为板状模型。

3.2 内固定模型生成

根据前期确定的内固定系统螺钉布局方案及设计的三因素三水平正交表，在Pro/E中完成上述9组试验的内固定系统装配工作，其中，第7组试验的内固定系统模型见图1。

图1 第7组试验内固定系统模型图

3.3 有限元模型生成

将内固定系统装配模型导入有限元分析软件ANSYS中，在股骨干中段切分出2 mm厚度的断片来模拟骨折状态，将该断片视为在骨折间隙中填充的相对股骨较软的材料。由于复杂的模型形状，可设置模型单元类型为十节点的四面体单元solid 187。假设研究中锁定螺钉、锁定钢板、股骨干及骨折填充物均为连续、均质、各项同性的线弹性材料，具体材料属性设置见表3。由于锁定螺钉与锁定钢板、锁定螺钉与股骨干之间无相对运动，故将锁定螺钉与锁定钢板、锁定螺钉与股骨干的接触关系设置为粘结状态[11]，经过切分形成的断片上下端与股骨干亦默认成粘结状态，完成对内固定模型的网格划分。

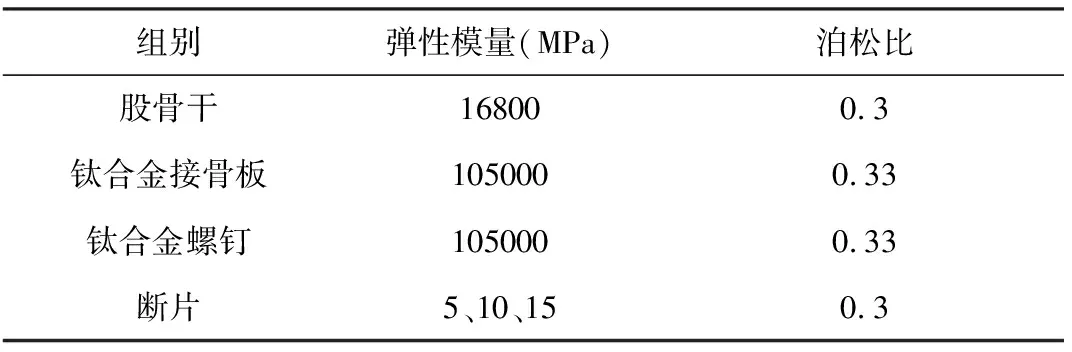
表3 材料属性设置

3.4 施加载荷并求解

考虑到正常成人单腿站立下股骨受力情况，设置大小为600 N的轴向载荷均匀的分布于股骨干近端的横截面，对股骨干远端底面进行位移全约束,其中第3组试验的具体约束与加载设置见图2。在ANSYS中使用默认求解器完成对有限元模型的求解计算，得出相应的等效应力云图与轴向变形图。

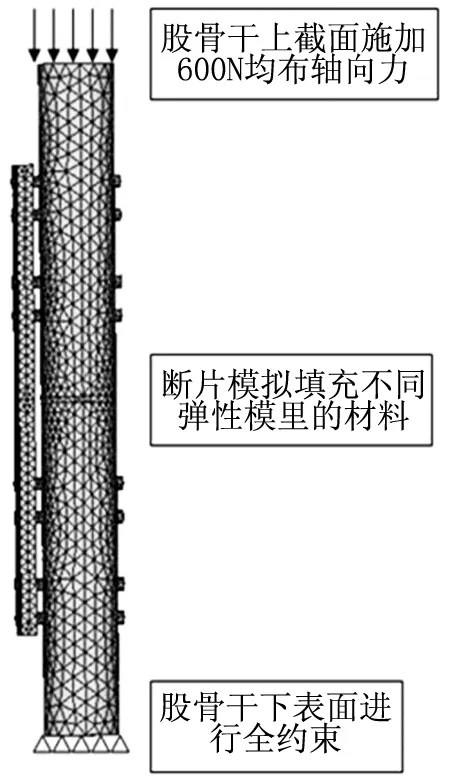
图2 第3组试验约束与加载设置图

4 结果与分析

4.1 结果

按照上述试验方案设计，完成所设计的9组试验的生物力学，得到三项主要指标的试验结果，试验结果见表4。在植入物最大等效应力方面，第1组试验的植入物最大等效应力出现在螺钉上，而其他各组均出现在接骨板上，其中9组试验植入物的最大等效应力出现在第6组的接骨板上，其等效应力云图见图3。而第7组试验股骨干的最大等效应力小于其他各组，其等效应力云图见图4。以试验第3组为例，其内固定系统等效应力云图见图5。在内固定系统最大轴向位移方面，第1、6、7组试验的最大轴向位移均超过了0.7 mm，而第3、5、9组也超过了0.3 mm。

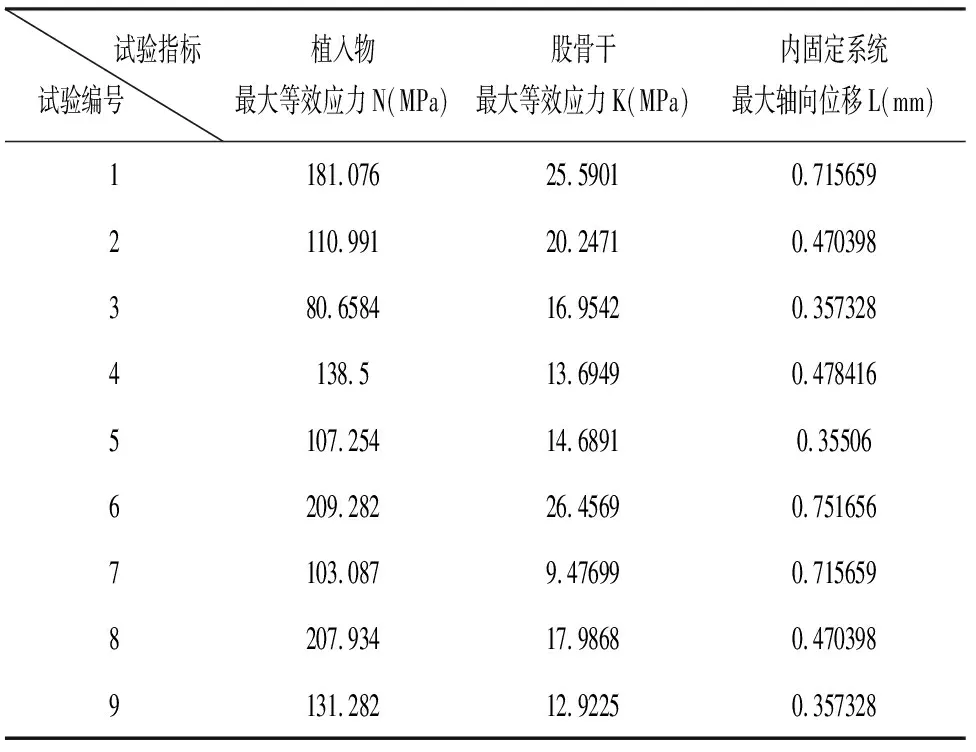
表4 试验结果

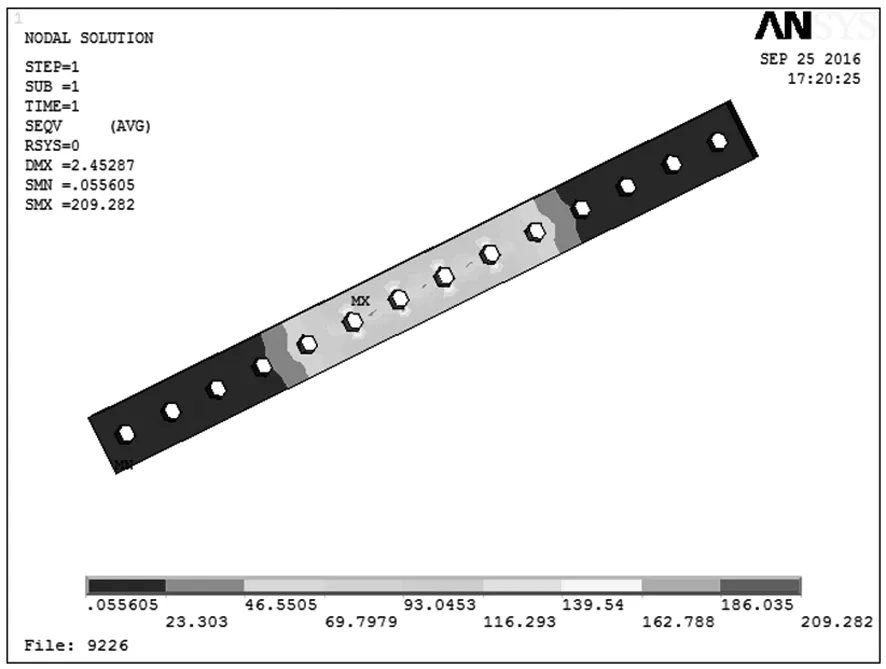
图3试验第6组接骨板的等效应力云图

Fig3Equivalentstresscontourmapoftheplateintheexperimentalsixthgroup

图4 试验第7组股骨干的等效应力云图

图5 试验第3组内固定系统的等效应力云图

Fig5Equivalentstresscontourmapoftheinternalfixationsystemintheexperimentalthirdgroup

4.2 分析

通过正交试验设计的9组试验, 每个因素中每一个水平都有3个试验, 且与其他因素的每一水平相遇且仅相遇一次[9]。本研究进行三因素三水平正交试验设计的生物力学分析，三个指标的直观分析表见表5。

表5 三个指标的直观分析表

由上述正交试验设计的考察指标直观分析可知，对于植入物最大等效应力来说，最优方案是A1B3C3；对于股骨干最大等效应力来说, 最优方案是A2B3C1；对于内固定系统最大轴向位移来说, 最优方案是A1B3C3，需要对三个方案进行综合考量。通过采用权矩阵分析方法，计算出影响试验结果的考察指标权重，可快速得出试验的最佳方案[12]。

据文献[13]，以表2为例，假设指标F越小越好，介绍权矩阵分析方法中权函数ω的求解过程：

因素层矩阵：

影响试验指标值的权矩阵：ω=M·T·S。

第一个考察指标为植入物最大等效应力，其值越小越好，权矩阵ω1计算如下：

ω1=M1·T1·S1=

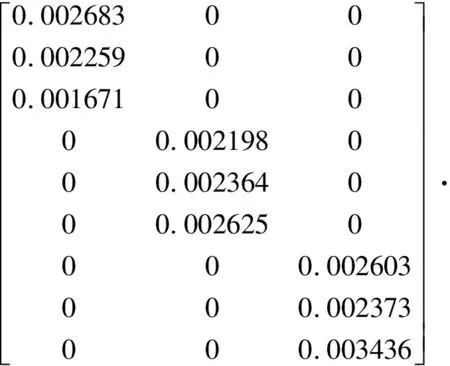
第二个考察指标为股骨干最大等效应力，其值越小越好，权矩阵ω2计算如下：

ω2=M2·T2·S2=

第三个考察指标为内固定系统最大轴向位移，其值越小越好，权矩阵ω3计算如下：

ω3=M3·T3·S3=

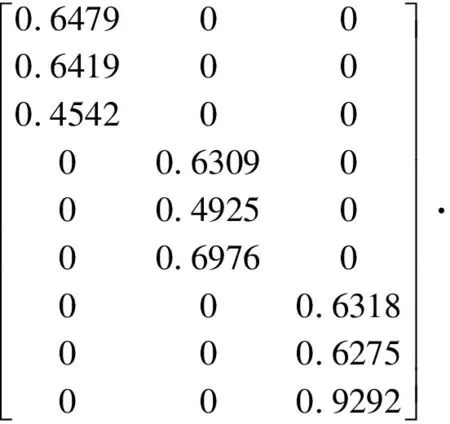
此正交试验考察指标的总权矩阵为三个指标值的权矩阵的平均值，计算如下：

综合上述计算，因素A的三个水平对试验结果的影响权重分别为：A1=0.1629、A2=0.1659、A3=0.1185，A2的权重最大；同理，因素B中B3的权重最大；因素C中C3的权重最大。由此可知，本研究中正交试验的最优方案A2B3C3，即螺钉直径为4 mm，锁定钢板与股骨表面间距为3 mm，骨折处填充物弹性模量为15 MPa。同时，可得出各个因素对正交试验考察指标影响的主次顺序为ACB。

5 讨论

近年来，有限元方法凭着其独有的的优势，越来越多的被应用于骨科植入物的研究中，为植入物临床使用提供实验依据。锁定钢板与骨干表面保持了一定间距，这很大程度的减少了对骨干表面血运的破坏[14]。本研究采用双皮质螺钉固定锁定钢板，提高骨折内固定系统的稳定性，缩短了股骨干骨折的恢复周期。

本研究将正交试验设计方法创造性的应用于骨折内固定系统多因素生物力学研究中，在保证了试验效果的同时，极大的减少试验数目。而正交试验直观分析法与权矩阵分析法的配合使用，不仅分别具体分析了三个因素三个水平上对每个指标的影响情况，而且得出了本研究中正交试验的最优方案及各个因素对正交试验指标值影响的主次顺序。

通过研究可知，对植入物最大等效应力、股骨干最大等效应力及内固定系统最大轴向位移来说, 螺钉直径A均是最主要影响因素。因素A、B、C的三个水平对试验结果的影响权重最大的分别为A2、B3、C3，即研究中本研究中正交试验的最优方案A2B3C3，各个因素对正交试验指标值影响的主次顺序为ACB。

在本研究中，对分析模型进行了简化，并作出了大量的假设，有效的保证了研究的简便性。在进行外力加载时，仅考虑了主要轴向受力的影响，而实际情况往往是肌肉及韧带等软组织的综合受力。研究中所考察因素的水平设置主要依靠医疗器械公司统计的临床数据来确定，须进行更加深入的探讨。在该课题的后续研究工作中，将逐渐完善分析中的不足，为相关临床治疗提供指导。