Fuzzy测度差的伪零可加与伪自连续性

陈 铭， 王立社

(湖州师范学院 理学院， 浙江 湖州 313000)

Fuzzy测度差的伪零可加与伪自连续性

陈 铭， 王立社

(湖州师范学院 理学院， 浙江 湖州 313000)

运用Fuzzy测度的概念，引入模糊测度差μ=μ1-μ2，在一定条件下证明μ仍是Fuzzy测度,并讨论Fuzzy测度差的伪零可加性以及伪下自连续性,最后探讨Fuzzy测度差的一致伪自连续性.

Fuzzy测度; Fuzzy测度的差; 伪零可加; 伪自连续; 一致伪自连续

MSC2010:94D05

1 基本知识

定义1.1[1-2]设X是一个非空集合,F是X上的σ-代数,一个非负广义实值集函数μ：F→[0,+∞]满足以下条件：

(1)μ(Ø)=0；

(2)A⊂B⟹μ(A)≤μ(B)；

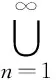
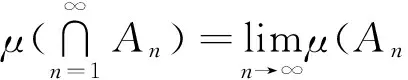
则称μ是一个Fuzzy测度,并称(X,F,μ)是一个Fuzzy测度空间.

定义1.2[3]对任意A∈F，μ(A)<∞,μ称为伪零可加的，如果对任意B∈A∩F，C∈A∩F,且μ(A-B)=μ(A),有：

μ(B∪C)=μ(C).

定义1.3[4]对任意A∈F,μ(A)<,μ称为伪上自连续的,如果

∀{Bn}⊂F,μ(Bn∩A)→μ(A),

则∀C∈A∩F,有:

μ((A-Bn)∪C)→μ(C).

定义1.4[5]对任意A∈F,μ(A)<,μ称为伪下自连续的,如果

∀{Bn}⊂F,μ(Bn∩A)→μ(A),

则∀C∈A∩F,有:

μ(Bn∩C)→μ(C).

如果μ既是伪上自连续的,又是伪下自连续的,则称μ是伪自连续的.

定义1.5[6-7]对任意∀A∈F,B∈A∩F,C∈A∩F,称μ是一致伪自连续的，如果对任意ε>0，存在δ=δ(ε)>0，当μ(A)≤μ(B)+δ时，有:

μ(C)≤μ(C∩B)+ε.

2 Fuzzy测度差

定理2.1 设μ1,μ2均为F上的有穷Fuzzy测度且∀A,B∈F，且满足B⊂A时，有：

μ2(A)-μ2(B)≤μ1(A)-μ1(B)，

令μ=μ1-μ2，其中:

∀E∈F,μ(E)=μ1(E)-μ2(E)，

则μ是一个Fuzzy测度.

证明

(1)μ(Ø)=μ1(Ø)-μ2(Ø)=0；

(2)B⊂A，由条件μ2(A)-μ2(B)≤μ1(A)-μ1(B)，有：

μ1(B)-μ2(B)≤μ1(A)-μ2(A)，

即μ(B)≤μ(A)；

(3)B1⊂B2⊂…,Bn∈F，注意到μ1，μ2均为有穷Fuzzy测度，则有：

(4)B1⊃B2⊃…,Bn∈F，注意到μ1,μ2均为有穷测度，则有:

定义2.2 满足定理2.1条件的Fuzzy测度μ=μ1-μ2称为Fuzzy测度μ1与μ2的差.

3 Fuzzy测度差的性质

定理3.1 如果Fuzzy测度μ1，μ2都是伪零可加的,则Fuzzy测度差μ=μ1-μ2也是伪零可加的.

证明∀A∈F,B∈A∩F,C∈A∩F，因为μ1，μ2都是伪零可加的，所以当

μ1(A-B)=μ1(A)，μ2(A-B)=μ2(A)

时，有：

μ(A-B)=μ1(A-B)-μ2(A-B)=μ1(A)-μ2(A)=μ(A).

再由

μ1(B∪C)=μ1(C),μ2(B∪C)=μ2C,

得:

μ(B∪C)=μ1(B∪C)-μ2(B∪C)=μ1(C)-μ2(C)=μ(C).

根据定义1.2得，μ=μ1-μ2是伪零可加的[8].

定理3.2 如果Fuzzy测度μ1，μ2都是伪上自连续的，则Fuzzy测度差μ=μ1-μ2也是伪上自连续的.

证明对任意A∈F，∀{Bn}⊂F，∀C∈A∩F,因为μ1，μ2都是伪上自连续的，所以当

μ1(Bn∩A)→μ1(A),μ2(Bn∩A)→μ2(A)

时，其中μ1(A)<∞，μ2(A)<∞,有:

μ(Bn∩C)=μ1(Bn∩A)-μ2(Bn∩A)→μ1(A)-μ2(A)=μ(A).

又由

μ1((A-Bn)∪C)→μ1(C),μ2((A-Bn)∪C)→μ2(C),

得:

μ((A-Bn)∪C)=μ1((A-Bn)∪C)-μ2((A-Bn)∪C)→μ1(C)-μ2(C)=μ(C).

根据定义1.3知，μ=μ1-μ2是伪上自连续的.

定理3.3 如果Fuzzy测度μ1，μ2都是伪下自连续的，则Fuzzy测度μ=μ1-μ2也是伪下自连续的.

证明对任意A∈F，∀{Bn}⊂F,∀C∈A∩F,因为μ1，μ2都是伪下自连续的，所以当

μ1(Bn∩A)→μ1(A),μ2(Bn∩A)→μ2(A)

时，其中μ1(A)<∞，μ2(A)<∞,有:

μ(Bn∩A)=μ1(Bn∩A)-μ2(Bn∩A)→μ1(A)-μ2(A)=μ(A).

又由

μ1((A-Bn)∪C)→μ1(C),μ2((A-Bn)∪C)→μ2(C),

得:

μ(Bn∩C)=μ1(Bn∩C)-μ2(Bn∩C)→μ1(C)-μ2(C)=μ(C).

根据定义1.4知，μ=μ1-μ2是伪下自连续的.

定理3.4 如果Fuzzy测度μ1，μ2都是一致伪自连续的，则Fuzzy测度差μ=μ1-μ2也是一致伪自连续的.

证明对任意∀A∈F,B∈A∩F,C∈A∩F，因为μ1，μ2都是一致伪自连续的，所以对任意ε1,ε2>0时，存在δ1=δ1(ε1)>0,δ2=δ2(ε2)>0,当

μ1(A)≤μ1(B)+δ1,μ2(A)≤μ2(B)+δ2

时，有:

μ1(C)≤μ1(C∩B)+ε1,μ2(C)≤μ2(C∩B)+ε2,

而

μ(A)=μ1(A)-μ2(A)≤μ1(B)+δ1-μ1(B)=μ(B)+δ1,

取δ=δ1,则当μ(A)≤μ(B)+δ时,有:

μ(C)=μ1(C)-μ2(C)≤μ1(C∩B)+ε1-μ2(C∩B)=μ(C∩B)+ε1.

由于ε1是任取的,由定义1.5知Fuzzy测度差μ=μ1-μ2是一致伪自连续的.

[1] LIU Y K,ZHANG G Q.On the completeness of fuzzy measure-space[J].Elsevier North-Holland Inc,1999,102(2):345-351.

[2] 张德利，郭彩梅.广义F积分的表示[J].模糊系统与数学，2000,14(1):31-35

[3] 哈明虎，程立新.关于模糊测度的伪零可加与伪一致自连续性[J].河北大学学报(自然科学版),1995,15(4):14-17.

[4] 王家芳.Fuzzy测度的伪自连续性[J].模糊系统与数学，1996，10(2):1-5.

[5] WANG Z Y.On the null-addictive and the autocontinuity of fuzzy measure[J].Fuzzy Sets & Systems,1992,45(2):223-226.

[6] SUN Q H.On the pseudo-autocontinuity of fuzzy measures[J].Fuzzy Sets and Systems,1992,45(1):59-68.

[7] 王立社.Fuzzy测度的和与乘积的伪零可加与伪自连续性[J].廊坊师范学院学报(自然科学版)，1997(3):14-16.

[8] 王立社.Fuzzy测度乘积零可加与自连续性[J].河北大学学报(自然科学版),1995,14(5):121-123.

MSC2010:94D05

FuzzyMeasureDifference'sPseudo-null-additivityandPseudo-autocontinuity

CHEN Ming, WANG Lishe

(School of Science, Huzhou University, Huzhou 313000, China)

This paper introduces the fuzzy measure differenceμ=μ1-μ2and proves thatμis still fuzzy measure in certain conditions. Then the pseudo-null-addictive, pseudo-auto-continuity and the uniform pseudo-auto-continuity of the fuzzy measure differenceμare investigated.

fuzzy measure; difference of fuzzy measures; pseudo-null-addictive; pseudo-autocontinuity; uniform pseudo-auto-continuit

2017-06-05

王立社，教授，研究方向:模糊数学.E-mail：wls12@zjhu.edu.cn

O159

A

1009-1734(2017)08-0006-03

[责任编辑高俊娥]