小学一年级解决问题典型错例分析及教学策略
张龙萍

【摘 要】一年级的全图式、半图半文式解决问题,看起来极其简单,学生作业中却错误百出。对此,文章从对错题进行整理汇总入手,分析产生错误的症结所在,找到有效的教学策略以便对症下药,从而帮助小学低年级学生切实提高解决问题的能力。
【关键词】一年级;数学;错例分析;教学策略
在新教材的使用中,我们发现解决问题是变动最大的一部分,学生在学习中总是存在一些顽固错误。笔者试着对一年级解决问题中学生比较容易错的题来个“病例大会诊”,希望以此提高解决问题启蒙教学的有效性,为今后解决稍复杂的问题打下坚实的基础。
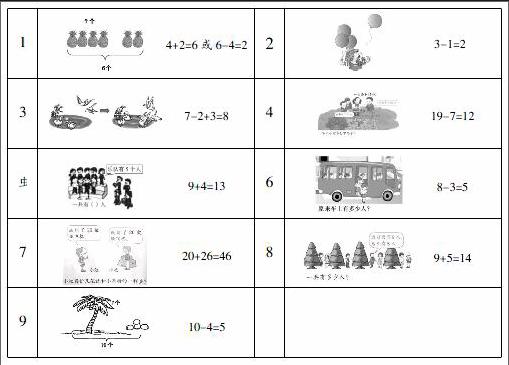
一、一年级学生在解决问题中出现的错例汇总
二、一年级学生在解决问题中产生错误的原因剖析
【错例1】主要有两种“病因”:(1)不理解大括号和问号的含义,不知道求什么,信息和问题混淆;(2)受“一图四式”的负迁移。“一图四式”中没有明确的问题指向,既可以写加法算式,也可以写减法算式,而此题有特定的问题,需要学生看清问号的位置,算式与图要对应起来。
【错例2、3】图片是静止的,学生从图上看到的往往是思维的结果,而不是思维的过程。因此部分同学对错例2,尤其是错例3理解起来很困难。如错例2中,学生只是直观地看到左边有3个气球,右边有1个气球,就列式3-1=2,无法按照事情发展的先后顺序整体感知图意,找准总数。
【错例4】此题文字较多,且含有无关信息,学生很难理解题意。
【错例5】学生在阅读信息时,往往先注意图片。这里学生没有看文字信息“乐队有5个人”,乐队人数是从图中数得的。
【錯例6】一般情况下,问题会与所描述的情境相对应,但错例6的情境描述与问题不太相符。出错的学生看到下车了3人,就想到用减法求出车上剩下的人数,在列式时更多地关注了情境而忽视了问题。
【错例7】问句“小红再折几架就和小亮折的一样多?”这样的表述学生难以理解。在一年级下册中,学生掌握了比多少的问题表述,但理解能力差的同学对这种新的表述方法难以接受。
【错例8】学生在解决问题时,直觉常常成为一种重要的策略,常以个别字词作为猜测的依据形成判断。一年级问题类型少,学生看见“一共”就直觉认为把说话同学前、后两部分人数加起来,忽略了说话的同学。
【错例9】在写得数时,学生并不是用计算的方法,而是直观地去数树上椰子的个数,受到图画的直观影响,就不假思索地把10减4算成了5。
三、应对一年级学生在解决问题中出现错误的有效策略
(一)重视指导,学会审题
一年级学生审题能力弱、缺乏分析题目的能力是造成错误的重要因素。因此,培养学生的审题能力是首要之举。
1. 在完整读的基础上读出关键信息
抓住关键句,进行重点标注。如错例4文字较多,就需要指导学生抓住关键句来读。先用铅笔点着文字读,明了题目大意后,边读边在题目中画上适当的记号。这道题的关键句是“小华比小雪多套中几个”(用括号括起来),比、多是关键词(点一下),小华、小雪套中的个数(标出来),捕捉关键信息,划去无关信息。
在图文结合的问题中,引导学生既看图又看文,但要精细阅读文字以获取正确信息。如错例5中,4是怎么来的?经过了解才知道,乐队人数是从图中数得的,学生并没有看文字信息“乐队有5个人”。这与学生对信息获取的优选性有关,因为人在读信息时,先注意的往往是图。因此,教师对此要有充分预设,有意识地引导学生在完整读的基础上以文字为准。
2. 化静为动,整体感知
对于一些难理解其意的情境图,可以通过演一演、动手操作等将静态画面还原为动态场景。如错例2、3,教师可以通过动态演示,将图片意思分层呈现。如错例3可以先呈现湖里有4只天鹅,然后飞走2只,再停几秒后飞来3只。动态演示后,让学生编题、列式。接着定格静态的情境图,让学生说一说箭头表示的含义,从中明白箭头表示左右两幅图之间有着动态的演变过程,并再次描述事情的发展过程。通过化静为动的演绎,为理解有困难的学生提供“拐杖”,使他们能准确、整体地感知图意。再安排类似的练习时,就可以直接呈现静态情境图,放手让学生在头脑中“放动画”,发挥想象说说事情的发展过程。
3. 信息重述,理解题意
学用三句话有序重述信息和问题。如错例6,让学生学着说:“下车3人,车上还剩5人,原来车上有多少人?”使学生在完整的表述中感悟信息和问题的关联。
4. 帮助学生将新问题转化为旧知识
学生在解决问题时,有时读了好几遍题,还是找不到解题的方法。这是由于他们不能将生疏的问题转化为自己熟悉的问题去解决。在错例7中,“小红再折几架就和小亮折的一样多?”部分学生不理解,不知从何入手。而这个问题的潜台词是小红折得少,小亮折得多。在教学时引导学生将这一问题转化为“小红比小亮少折几架?”或“小亮比小红多折几架?”这两个熟悉的比多少的问题。如此一转化使原本难以理解的新问题变成学生容易理解的旧问题,解答时就能如鱼得水。
(二)精彩的例举使数量关系更形象、具体
理清数量关系,才能“知其所以然”地解决问题。数量关系很抽象,只有和具体的情境相结合,才能形象具体。因此,要让学生联系生活实际举例子,结合例子说清数量关系。
例如,在教学《减法的初步认识》时,笔者出示了一幅气球图。
师:原来有4个气球,飞走了1个,还剩几个?可以怎样列式?
生1:4-1=3。
师:为什么用减法解决?
生1:因为4个气球中飞走了1个,就少了1个,所以减去1,剩下3个。
师:是呀,4个是总数,1个是飞走的部分,因为总数-飞走的=剩下的,所以用4-1=3计算。
笔者请学生用简练的语言表达图中3个数量的关系,而这个关系正是用减法解决这个问题的依据。
师:生活中还有许多像这样数量变少用减法解决的例子,你能说一说吗?
生2:有4张白纸,用了2张,还剩几张?4-2=2。
师:为什么用减法?
生2:因为总数-用了的=剩下的。
生3:停车场有5辆汽车,开走了2辆,还剩几辆?5-2=3。
师:为什么用减法?
生3:因为总数-开走的=剩下的。
……
师:我们刚才说的“飞走的”、“用了的”、“开走的”……都是总数中的一部分,是“去掉”的部分,总数-“去掉”的部分=剩下的部分。
这样,学生亲历了“减法”意义的建构过程,在具体情境中理解了总数与部分数之间的数量关系,为下一阶段解决问题的教学打下了坚实的基础。
(三)强化学生的问题意识
1. 从无到有,内驱产生问题
一年级学生对事物的认识总是先入为主,受第一印象影响深刻。如果直接出示错例1,引发不了问题意识,学生不免纳闷:“明明已告知答案(左边有4个菠萝),为什么还要算?”有无病呻吟之感,缺乏提出问题的内驱力。于是,笔者先遮住左边部分,呈现问号,让学生有明确的问题感;接着练习有问号,也有不完整的图示信息;再到“一图四式”,提供全部信息,请学生选择其中两个,想象假设在图中不同处打问号,从不同角度提出完整的数学问题。这样从问题呈现图示内容的“无”逐渐到“有”,学生的问题意识愈加深刻,才能对“?”郑重其视。
2. 细致类比,使数量关系的转化更有理、易懂
数量关系中三个量可以相互转化,由其中任意两个量就能求出第三个量。而学生在思考时,往往单一地往一个方向思考,逆向思维能力较弱。因此,在图文问题中渗透数量关系间的转化是非常必要的。例如,笔者利用图1、2、3进行类比。
师:这3幅图有什么相同点?
生:画的都是菠萝,左边有4个,右边有2个,一共有6个。
师:有什么不同?
生:问号位置不同。
师:也就是什么不同了?
生:问题、信息不同了。
之后,笔者让学生用3句话分别描述这3幅图的信息和问题,分析数量关系。
图1:左边有4个,右边有2个,一共有几个?4个是左边的数量,2个是右边的数量,这两个数量怎样计算才能求出总数量呢?左边的数量+右边的数量=总数量,4+2=6。
图2:一共有6个,右边有2个,左边有几个?6个是总数量,2个是右边的数量,这两个数量怎样计算才能求出左边的数量呢?总数量-右边的数量=左边的数量,6-2=4。
图3:一共有6个,左边有4个,右边有几个?6个是总数量,4个是左边的数量,这两个数量怎样计算才能求出右边的数量呢?总数量一左边的数量=右边的数量,6-4=2。
师:图中3个数量之间有什么关系?
生:这3个数量可以变来变去,调换位置。
师:也就是说,3个数量只要知道其中2个就能求出第3个。
学生虽然无法用“相互转换”这个词确切表达相关联的3个数量间的关系,但从他们稚嫩的语言中可以感受到他们已经意会了。理解数量关系间的转化,能提高逆向思维能力,解决问题就更加轻松、灵活、有依据。
3. 借助画图,感悟理解
一年级学生以直观形象思维为主,单纯地从抽象的文字中理解题意、分析数量关系很难。怎么办?可以训练学生使用画图策略。如出现错例8时,笔者设计如下:
师:这样解决对吗?用你喜欢的符号把题意表示出来,你发现了什么问题?
(学生尝试画图)
师:说说你是怎么画的?
生1:我先画了一个大圆表示说话的同学,然后在大圆的前面画了9个小圆,后面画了5个小圆,我数了一下一共是15个圆,这题应该一共有15人,14人这个答案是错的。
师:这个同学是用圆来表示的,你是用什么来表示的?
生2:我用正方形表示说话的同学,然后用三角形表示他前面和后面的人,我也发现合起来是15人。
师:尽管他们用的图形不一样,但每个图形都代表一个人。仔细观察,14人这个答案错在哪儿?要想求出一共有几人到底该怎么列式?
生2(迫不及待地):说话的同学漏算了!应该是9+5+1=15(人)。
师:真善于观察,一共的人不仅包括排在这个同学前面和后面的人,还包括他自己!(将学生图中的大圆和正方形描红)看来,画图能清楚地表示出这道题的意思,让我们一看就能明白。
4. 反思训练,积累经验
反思和检验,应该是解决问题的压轴戏,它有利于培养学生的反思能力和实践应用能力。解答完题后,要有目的地引导学生思考:收集了哪些信息,有无遗漏?为什么这样列式?算式中的每个数字表示什么意思?请学生回顾反思自己的解答是否正确或合理,以得到强化或矫正。如错例9,可以引导学生把结果5个椰子放到“?”处检验,树上5个与地上4个合起来是9个,发现与已知信息一共有10个不符。为什么树上只画了5个椰子?经过反思,学生就会意识到另一个椰子被树叶遮住了,此处用直觀数的方法不准确,应该采用计算的方法。像这样,通过有意识地长期训练,可以逐步培养学生思维的自觉性,同时积累更多的解题经验。
“学习是一种渐进的尝试错误的过程”,没有错误就没有真正意义上的学习。学生出错是难免的,作为教师要乐于错中寻源,积极探索每一错题背后的有效教学策略,真正做到因学定教,进而达到减少学生解决问题中顽固错误的目的,使数学教学更为有效。

