城市轨道列车发车间隔的优化方法研究

刘东晓，姜志侠，周圣杰

（1.长春理工大学 理学院，长春 130022；2.长春理工大学 电子信息工程学院，长春 130022）

城市轨道列车发车间隔的优化方法研究

刘东晓1，姜志侠1，周圣杰2

（1.长春理工大学 理学院，长春 130022；2.长春理工大学 电子信息工程学院，长春 130022）

在城市轨道交通中，考虑乘客和运营商两方面的利益，以车站等候人数最少和运营商经济效益最高为优化目标，建立了发车间隔优化模型。基于模糊目标规划，利用lingo软件对模型进行求解。在实际生活中，基于客流聚集特征和线路运营之间的协调关系，建立的城市轨道列车发车间隔优化模型，在安全运营列车的条件下对于提高线路运营效率、减小交通压力有非常重要的意义。

城市轨道交通；优化；模糊目标规划；发车间隔

城市轨道交通的运营是路网运营的关键环节，考虑到客运压力的不断增大而列车运输潜力一定的现状，在安全运营的条件下研究优化基于客流的城市轨道列车发车间隔势在必行。国内关于行车间隔的研究主要有：郑晓龙等［1］基于对城市轨道交通系统列车间隔的影响因素的分析，推导得出不同闭塞方式下列车间隔的计算公式，提高线路整体的通行能力，缓解髙峰时期客流压力；史瑞洁［2］、方蕾［3］、严波［4］等建立了不同目标的行车间隔模型；邵伟娟［5］提出基于客流的城市轨道交通线路协同安全运营优化方法。国外，Yuhem C，Chunghsing.Y［6］以总运营成本最低和乘客旅行时间最低为目标建立了优化城市轨道交通列车时刻表的多目标整数规划模型；Harris and Anderson［7］对列车停站时间的估计模型中的各个时间段都进行了分析。目前国内外学者从客流分布发车计划等多方面做了大量研究，为研究轨道交通的安全运营提供了一定的基础和理论依据。

目前，大多数基于客流的城市轨道交通运营的研究还局限于对客流的预测和分配等传统的客流统计、分析，不能适应现阶段复杂多变的交通运营环境。本文基于列车的运行过程和线路的运营过程之间的关系，考虑行人和运营商两方面的利益，以在一条线路上的客流高峰时间段内车站等候人数最少、单位成本的经济效益最高为目标函数，以线路运营安全为约束条件，建立了城市轨道交通列车发车间隔优化模型，基于模糊目标规划求解得到一种综合了两个目标需求的合理的发车间隔方案。

1 城市轨道列车发车间隔优化模型的建立

1.1 前提假设

为解决一条城市轨道交通线路在客流高峰时间段内的安全运营问题，在断面客流量为已知的情况下，综合考虑客流聚集特征和线路运营之间的关系，建立优化列车发车间隔模型，提出如下假设：统计时间段内各车站的乘客到站服从均匀分布，且遵循先到先服务的原则；列车到站停稳后，乘客先下后上；列车在运行过程中每站都停，不会跨行和越线停车；线路上列车的型号固定，每辆列车的最大载客量为Cmax，额定载客量为C。

1.2 目标函数的建立

目标函数I：车站等候人数最少

如果城市轨道交通线路上一共有m个车站，而一条轨道线路上相邻两个车站之间为一个行车区间，那么轨道线路就会被分割成m-1个行车区间。把时间段T作为完整的统计时间段，细划为nr个时间段，其中第j个时间段的时间长度为ΔTj(j=1,2,...,nr)，第j个时间段的列车发车间隔为hj，在第j个时间段内从行车区间i-1到i的断面客流量为Qij(i=1,2,...,m-1)。每一个时间段车站的等候人数就是在每个时间段的总客流量减去在这个时间段的列车额定载客量与发车数的乘积，因此，在统计时间段T内，车站的总等候人数为所有被划分的小时间段上车站等候人数的和。当在整个统计时间段T内车站总等候人数达到最小值时，充分考虑了行人的利益，让行人能够舒心的乘坐列车。故目标函数I为：

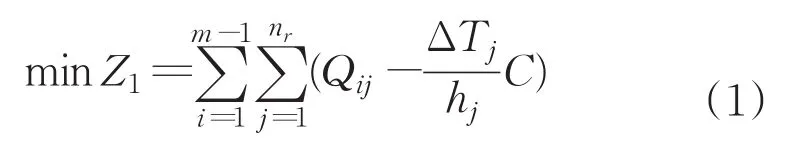
目标函数II：单位成本的经济效益最高

城市轨道线路上，在第j个时间段内从行车区间i-1到i的断面客流密度为λij，其中此时，列车运载的乘客总数为Fij，列车运载乘客总数应为在所有车站所有时间段上断面客流密度与发车间隔乘积的总和，即：

按照轨道交通运营单位票价制定原则，人均单位票价M＝人均运营成本P*（1+利润率a）。在统计时间段内，运营收入=列车运载乘客总数*人均票价，即：

单列车额定运营成本=列车额定客流量*人均运营成本。整个统计时间段上线路的运营成本=单列车列车额定运营成本*整个统计时间段被划分的时间段数。当列车运营商在整个统计时间段内的单位成本的经济效益达到最高时，也就意味着充分考虑了列车运营商的利益，让运营商有充分的动力安全运营轨道线路。故目标函数II为：

1.3 约束条件

为保证城市轨道交通线路能够安全运营，目标约束主要有：

约束条件1：列车实际载客数不能超过列车最大载客量Cmax。列车的实际载客量如果超过列车的最大载客量，列车将很容易发生刹车失灵等交通事故。因此，为保证行车安全应要求列车实际载客量不能超过列车最大载客量。

约束条件2：列车发车间隔不能过小也不能过大。若列车发车间隔过小，两车之间很容易发生追尾事件；若列车发车间隔过大，可能导致车站等候人数超出车站站台的容纳能力，使行人行动不便，严重时可能发生踩踏事件。因此，为保证行人和列车行驶安全应要求发车间隔不能过大或过小。

可如下表示约束条件：

1.4 基于模糊目标规划的模型求解理论

假设模型有n个目标函数Zq(q=1,2,...,n)，用模糊目标规划求解多目标规划的有效解的步骤为：

（2）计算反映各目标函数重要性的伸缩性指标lq(lq≥0)；

（3）给出模糊目标集Gq的隶属度函数；

当求目标函数的最小值时：

当求目标函数的最大值时：

（4）求解模糊目标集Gq，令等价于求以下线性规划问题：

该线性规划的最优解即为原多目标规划问题的有效解。

2 上海地铁1号线发车间隔优化方案

以2015年4月30日上海地铁1号线富锦路站到莘庄站为例建立城市轨道列车发车间隔优化模型。上海地铁1号线采用8节A型列车方案，A型列车一节车厢的额定载客量为310人，最大载客量为410人，因此列车额定载客量C=2480，最大载客量Cmax=3280。考虑到列车行驶和行人的安全，目标设计发车最小发车间隔为2分钟，最大发车间隔为10分钟。

表1 上海地铁1号线断面客流量（T=150分钟）

2.1 数据处理及分析

为了优化早高峰7：00-9：30时间段，即统计时间段T=150分钟，上海地铁1号线（车站数m=28）列车的发车间隔，将整个统计时间段划分为nr=5个时间段，每个小时间段为30分钟，对应的发车间隔即决策变量设为h1、h2、h3、h4、h5，其中列车运营商的利润率a=20%。通过对上海地铁卡的刷卡记录进行统计得到上海地铁1号线断面客流量，如表1所示，进而用表1中的数据进行列车发车间隔优化模型的求解。

2.2 模型的建立与求解

由式（1）-（4）建立多目标整数规划模型：

目标函数I：车站等候人数最少

目标函数II：单位成本的经济效益最高

由式（3）、（4）可计算出约束条件为：

其中，h1、h2、h3、h4、h5取整数。

首先，用lingo软件求得目标函数I在约束条件（11）下的最优解为：

h1=2分钟，h2=2分钟，h3=2分钟，h4=2分钟，h5=2分钟，Z1的最小值此时将求得的发车间隔带入式（10）中求得目标函数II的值

其次，用lingo软件求得目标函数II在相同约束条件（11）下的最优解为：

h1=8分钟，h2=5分钟，h3=6分钟，h4=10分钟，h5=10分钟，Z2的最大值此时将求得的发车间隔带入式（9）中求得目标函数I的值

根据模糊目标规划求解：

令G=G1G2，等价于求解以下线性规划问题：

该线性规划的解，即多目标规划的有效解为：

h1=8分钟，h2=5分钟，h3=2分钟，h4=2分钟，h5=2分钟，此时Z1=651460，Z2=11.9739。

由模糊目标规划求解得到的发车间隔方案可以看出，在早高峰时间段内，上海地铁1号线在7：00-7：30时间段内发车间隔应为8分钟，在7：30-8：00时间段内发车间隔应为5分钟，在8：00-9：30时间段内发车间隔为2分钟。现阶段，上海地铁1号线在早高峰7：00-9：30时间段的发车间隔为2分钟44秒，由此可计算上述两个目标函数的值分别为Z1=651142.439，Z2=6.9413。两者相比可以看出，虽然在现阶段发车间隔为2分钟44秒的情况下车站的等候人数少一点，但单位成本的经济效益降低了很多，且车站的等候人数几乎没有差别，相差数很小，因此，根据模型求解得发车间隔更好。在该模型得到的发车间隔方案综合考虑了列车运营商和行人两方面的利益，并在保证列车行驶和行人安全的基础上，使上海地铁1号线的列车运营效率有所提高，有效的缓解交通压力。

3 结论

城市轨道交通是城市公共交通的重要组成部分。现阶段，城市轨道交通中的大客流量与有限的运输能力之间的矛盾不断突出，因此，在列车安全运营的条件下研究优化基于客流的城市轨道交通的运营势在必行。本文深入研究了在线路运营层面上代表客流风险的指标即客流密度，结合列车运行过程，建立了基于客流的城市轨道交通发车间隔优化模型，利用模糊目标规划理论求解在两个目标需求下的合理的发车间隔方案。结合上海地铁1号线的实例分析可以看出细分客流统计时间段，更能有效的利用客流随时间变化的规律，在满足目标需求的条件下求解合理的发车间隔方案，并与上海地铁1号线真实的发车间隔比较得到根据模型求解的发车方案更好的结果，且模型的计算效率高，可实施性强，为城市轨道交通的运营提供了新的参考思路。

［1］郑晓龙，马琳，唐涛，等.城市轨道交通系统中列车间隔的有关分析［J］.交通与计算机，2005，23（3）：26-28.

［2］史瑞洁.城市轨道交通运营组织优化研究［D］.成都：西南交通大学，2011.

［3］方蕾，庞志显.城市轨道交通客流与行车组织分析［J］.城市轨道交通研究，2005，7（5）：42-44.

［4］严波.城市轨道交通行车间隔优化模型研究［J］.城市轨道交通研究，2008（6）：53-57.

［5］邵伟娟.基于客流的城轨交通线路协同安全运营优化方法研究［D］.北京：北京交通大学，2016.

［6］Yu-Hern Chang，Chung-Hsing Yeh，Ching-Cheng Shen.A multiobjective model for passenger train services planning：application to Taiwan’s high-speed rail line［J］.Transportation Research Part B，2000，34（2）：91-106.

［7］Harris Nigel G，Anderson R J.An international comparison of urban rail boarding and alighting rates［J］.Proceedings of the Institution of Mechanical Engineers Part F：Journal of Rail and Rapid Transit，2007，221（4）：521-526.

Study on Optimization Method of Departure Interval of Urban Rail Transit Train

LIU Dongxiao1，JIANG Zhixia1，ZHOU Shengjie2
（1.School of Science，Changchun University of Science and Technology，Changchun 130022；2.School of Electronics and Information Engineering，Changchun University of Science and Technology，Changchun 130022）

In the urban rail transit considering the interests of both passengers and operators，the optimization model of the departure interval is established based on the minimum number of passengers waiting for the station and the highest economic benefit of the operators.Based on the fuzzy goal programming，the lingo software is used to solve the model.In the real life，the optimization model of urban rail transit interval is established based on the coordination relationship between passenger flow characteristics and line operation.The model is very important for improving the operation efficiency and reducing the traffic pressure under the condition of safe operation of trains.

urban rail transit；optimization；fuzzy target planning；departure interval

U292.4

A

1672-9870（2017）04-0115-05

2017-06-12

国家自然科学基金资助项目（51378076）

刘东晓（1992-），女，硕士研究生，E-mail：1297732180@qq.com

姜志侠（1976-），女，博士，教授，E-mail：zhixia_jiang@126.com