求解模糊最短路问题的动态规划法

李 红 霞

(陇东学院 数学与统计学院，甘肃 庆阳 745000)

求解模糊最短路问题的动态规划法

李 红 霞

(陇东学院 数学与统计学院，甘肃 庆阳 745000)

提出动态规划法求解模糊最短路问题。对于给定起点和终点的有向模糊图，可以从终点出发，逆向追溯分阶段探寻最短路，同时删去非最短路。而对于每个阶段的最短路问题，给出了求解最短路长度和最短路的方法，即利用模糊最小算子求最短路长度，并根据每条路与最短路长度的贴近度来确定最短路。最后通过例子说明此种方法的可行性和有效性。

模糊数；最短路；动态规划

Abstract： The dynamic programming method for solving fuzzy shortest path problem is given.For the fuzzy graph with a given starting point and end point,we can reversely explore the most short circuit from the end point in stages,and delete non shortest path.For the shortest path problem in each stage,a method to calculate the shortest path length and the shortest path is presented to solve the shortest path length by using the fuzzy minimum operator and to determine the shortest path according to the closeness of each road with the shortest length.Finally the validity and feasibility of this method is illustrated through an example.

Keywords： fuzzy number;the shortest path;dynamic programming

最短路问题是经典的网络优化问题。在经典网络图中,两点之间的边不仅表示距离,而且还表示时间,运费等,而这些涉及到路况、库存等许多因素的量一般都是不确定的,因而用模糊数表示不失为一种有效方法。对于由有限个顶点和有向边构成的网络,假定每两个点之间都存在有向边,边的权重都表示为模糊数,于是路的长度即为组成路的边权之和,找到长度最短的路即为模糊最短路问题。Dubois和Prade[1]首先进行模糊最短路问题的研究,其算法是推广了经典的Floyd和Ford-Moore-Bellman算法。Okada和Gen[2,3]等推广了Kjikstra算法。Takaoka[4]通过信息共享改进了一类特殊图最短路问题的计算复杂度。Dou[5]给出了最优,最劣的模糊理想路,比较所有路与模糊理想路的相似度,从而得到最优路。Cheng[6]给出了约束条件的最短路问题,其边为独立的正态分布,并提出了分支定界算法。关于最短路问题的研究可参阅文献[7-10]。然而我们考虑到,在寻找最优，最劣路的过程中，如果从顶点到终点的所有路中去考察,计算量会很大，同时还可能遗漏掉某些路,因此这个过程异常复杂。。由于最短路的子路应该是最短路，如果分阶段进行并且删去子路的非优路将会减少计算量。因此本文给出了基于模糊理想路的动态规划方法，从目标点出发逆向搜索最短路，同时删去非最优路，而对于每个阶段的最短路问题，给出了求解最短路长度和最短路的方法，即利用模糊最小算子求最短路长度，并根据每条路与最短路长度的贴近度来确定最短路。最后通过例子说明此种方法的可行性和有效性。

1 基础知识

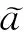
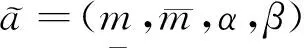
其中α,β分别为左右扩张。

下面给出模糊数的加法运算和序关系:

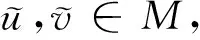
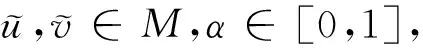
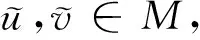
此定义较不适合计算，我们给出下面的等价定义1.6，利用模糊数的α水平集表示，更加符合人们的直觉。

2 模糊图及模糊最短路

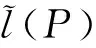
在有向图中，给定起点和终点的所有路有n条，其模糊长度为Li(i=1,2,…,n)，我们给出求最短路长度的步骤如下：

第一步：置L=L1，令i=2。

第二步：根据公式计算L=min(L,Li)。

第三步：i=i+1，重复第二步到第三步，直到i=n+1。

上述过程可以用下面例子来说明：

假定有四条路，其对应的模糊长度用梯形模糊数表示为：L1=(30,40,10,5),L2=(25,45,6,8),L3=(25,33,3,2),L4=(33,38,6,5)。

第一步：置L=L1=(30,40,10,5),令i=2。

第二步：计算L=min(L,Li)=min(L,L2)=(25,40,6,8)。

第三步：i=i+1，重复第二步到第三步，直到i=5。由此我们得到L=(25,33,6,2)。

为了求出模糊最短路,我们求每条路与最短路长度的贴近度，与最短路长度最贴近的即为最短路。关于模糊贴近度的研究也比较多,其定义如下：

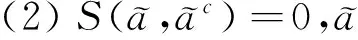
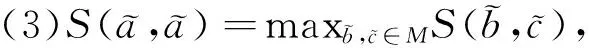
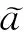
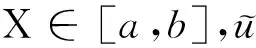
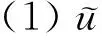
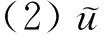
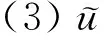
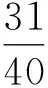
3 用动态规划法求模糊最短路

对于有始点和终点的有向模糊图，我们可以从终点出发，逆向溯源，分阶段寻找最短路，删掉显然的非最短路，同时可以简化运算量。对于有向模糊图，根据模糊路的长度的计算，模糊最短路有下面的定理:

定理3.1 设G(V,A)为有向模糊图,路pst={s,(s,v1),v1,…,vi-1,(vi-1,vi),vi,…，(vn,t),t}为顶点s到t的路，则pst为最短路当且仅当从顶点s到任意中间点vi的子路psvi为s到vi的最短路。

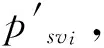
设有向图G(V,A)由有限个顶点V={1,2,…,n}和m条有向边A⊆V×V构成,对于从始点1到终点n的模糊最短路问题，我们给出如下动态规划法算法：

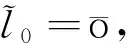
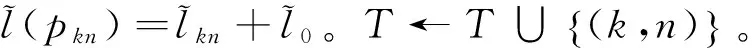
第三步：对每个顶点i,使得(i,j)∈A，执行下面(1)到(3)。

第四步：找出从顶点1到n的最短路。

下面我们借用文[12]中的例子来介绍动态规划法。

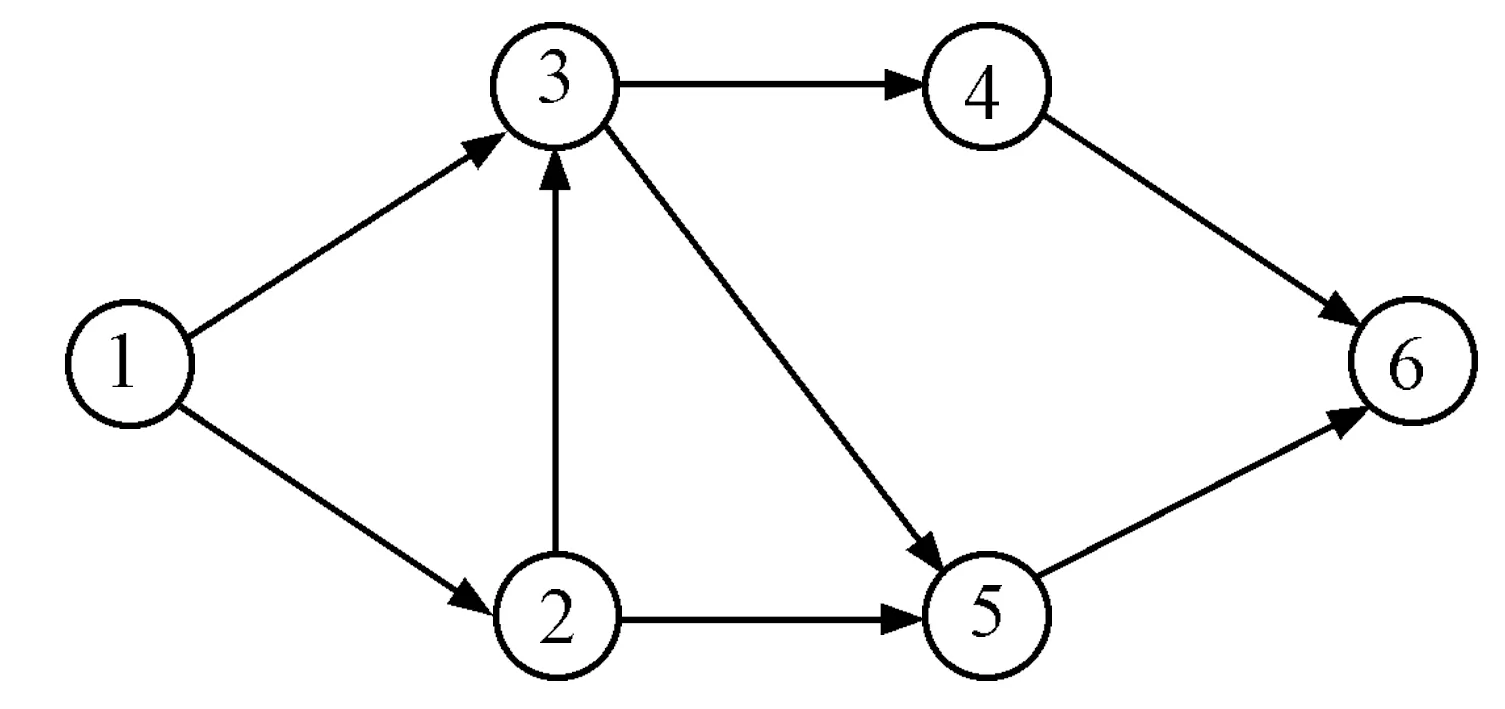
图1

图1中两点i和j之间的有向弧长度分别用梯形模糊数lij来表示，l12=(20,20,10,10),l13=(62,65,10,5),l23=(38,40,3,5),l25=(55,60,3,5),l34=(13,17,3,3),l35=(9,9,1,1),l46=(75,85,5,12),l56=(70,80,20,20),我们要利用动态规划法计算从顶点1到6的最短路。

这可被看作三阶段动态规划问题。第一阶段从顶点5开始，因为从顶点5到6只有一条路，其模糊长度为(70,80,20,20),则路5-6为输入点为5的最短路。同时，从顶点4到6只有唯一的路4-6，其模糊长度为(75,85,5,12),也是输入点为4的最短路。

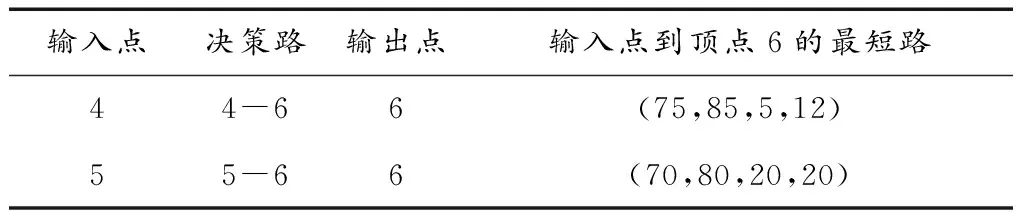
表2 第一阶段

第二阶段从顶点3开始，有两条路3-4-6和3-5-6，其模糊长度分别为(88,102,8,15),(79,89,21,21),根据第二节的算法，3-5-6为从顶点3输入的模糊最短路，删去3-4-6。对于顶点2，有2-3与2-5两条路，通过计算，2-3-5-6为顶点2输入的模糊最短路，删去2-5-6。

第三阶段从顶点1开始，类似地，得到1-2-3-5-6为模糊最短路，其长度为(137,149，34,36)。这个结果与文[12]中的应用标签法计算的结果相同,由此前面的动态规划法计算模糊最短路问题不失为一种有效的算法。

第二阶段(删去3-4，2-5)

第三阶段(删去1-3)

4 小结

模糊最短路问题的广泛应用已引起许多学者的关注。对于决策者来说，模糊最短路长度和相应的模糊最短路是重要的信息。这篇文章试图找到模糊最短路长度和模糊最短路。首先给出了求解模糊最短路长度和模糊最短路的方法，对于n条路，利用模糊最小和贴近度找到模糊最短路长度和模糊最短路。其次，在给定始点和终点的模糊有向图中，从终点出发，我们给出了逆向追溯的动态规划方法，在非最优路的删除过程中，计算量将会减少。因而，对于较复杂的网络图来说，所提出的方法不失为一种有效方法。

[1]D.Dubois,H.Prade.Fuzzy Sets and Systems:Theory and Applications[M].New York:Academic Press,1980,144(3):370-374.

[2]S.Okada,M.Gen.Order relation between intervals and its applications to shortest path problem[C],in:Proc.15th Annu.Conf.on Computers and Industrial Engineering,Vol.25,1993.

[3]S.Okada,M.Gen.Fuzzy shortest path problem[C],in: Proc.16th Ann.Conf.on Computers and Industrial Engineering,Vol.27,1994.

[4]T.Takaoka.Sharing information for the all pairs shortest path problem[J].Theoretical Computer Science,2014(520):43-50.

[5]Y.L.Dou,L.C.Zhu,H.S.Wang.Solving the fuzzy shortest path problem using multi-criteria decision method based on vague similarity measure[J].Applied soft computing,2012(12):1621-1631.

[6]J.Q.Cheng,A.Lisser.Maximum probability shortest path problem[J].Discrete Applied Mathematics,2015(192):40-48.

[7]D.Cantone,S.Faro.Fast shortest paths algorithms in the presence of few destinations of negative weight arcs[J].Journal of dscrete algorithms,2014(24):12-25.

[8]杨晓凌.最短路及最小支撑树的灵敏度分析[D].长沙：国防科学技术大学，2007:5-8.

[9]Shinkoh Okada.Fuzzy shortest path problems incorporating interactivity among paths[J],Fuzzy sets and Systems,2004(142),335-357.

[10]F.Hernandes,M.T.Lamata,J.L.Verdegay,A.Yanakami.The shortest path problem on networks with fuzzy parameters[J].Fuzzy Sets and Systems,2007(158):1561-1570.

[11]吴从炘,马明.模糊分析学基础[M].北京：国防工业出版社,1991:56-60.

[12]S.Okada,T.Soper.A shortest path problem on a network with fuzzy arc lengths[J].Fuzzy Sests and Systems,2000(109):129-140.

【责任编辑朱世广】

TheDynamicProgrammingMethodforSolvingtheFuzzyShortestPathProblem

LI Hong-xia

(CollegeofMathematicsandStatistics,LongDongUniversity,Qingyang745000,Gansu)

O159

A

1674-1730(2017)05-0001-04

2016-11-12

甘肃省高等学校科研项目《模糊图在网络优化中的应用研究》(2015A-144)；2016年度甘肃省“十三五”教育科学规划课题《地方高校师范专业教师职业技能嵌入式培养的应用研究》(GS[2016]GHB1255)

李红霞(1970—)，女，甘肃庆阳人，副教授，硕士，主要从事模糊分析与模糊图的研究。