基于MATLAB的光传播特性的数值计算

郑兴荣，宋小永，郑燕飞，王 琪，姜 蓉

(陇东学院 电气工程学院，甘肃 庆阳 745000)

基于MATLAB的光传播特性的数值计算

郑兴荣，宋小永，郑燕飞，王 琪，姜 蓉

(陇东学院 电气工程学院，甘肃 庆阳 745000)

基于物理光学理论和麦克斯韦电磁理论，通过对波动方程和菲涅耳公式的推导，研究了电矢量在介质表面的光传播特性。运用Matlab软件对光传播特性进行了数据计算和仿真模拟。结果表明：光在介质面传播时会引起反射和折射，光的反射和折射特性主要取决于电矢量的振动；影响介质面反射、折射特性的因素主要有三个，分别是入射角、介质折射率和入射光的波动特性；利用MATLAB得到了光在介质面上传播的各种特性曲线；光以不同入射角穿过两介质面时，反射光与折射光的相位、振幅以及能流等都会发生相应的变化。通过特性曲线可以看出：光以布儒斯特角入射时会发生全偏振现象；以大于临界角入射时发生全反射现象，发生全反射时能流透射率为0；随着入射角变化，反射光与透射光各分量相位发生突变或渐变，并因此造成半波段或整波段的损失。

光传播特性；数值计算；仿真模拟；Matlab软件

Abstract： Based on physical optics theory and maxwell’s electromagnetic theory,the propagation characteristics of light from the dielectric surface are studied by deducing wave equation and Fresnel formula.By using Matlab software,we calculated and simulated the propagation characteristics of light.These conclusions can be drawn that the propagation of light from dielectric surface can cause the optical reflection and refraction which mainly depends on the vibration of the electric vector.The factors which influence the optical reflection and refraction are incident angle,refractive index and the wave characteristics of incident light.By using MATLAB software,we obtained the various characteristic curve of light travel.When the light go through the two dielectric surfaces under different incidence angle,the reflected light and the phase,amplitude and energy flow of the refracted light will accordingly change.We found that only when the incidence zenith angle is equal to Brewster angle,the polarization phenomenon is occurred.The transmissivity of energy flow is 0 when total reflection phenomenon occurs,and the change of incident angle causes the loss of half or the whole wave band.

Keywords： propagation characteristics of light;numerical calculation;simulation;MATLAB software

光特性的研究在生产生活中具有十分重要的意义。在工业上,它广泛应用于通讯业,计算机业,制造业及数据存储等的产品中。对于与之相关的物理现象，光作为一种电磁波,其在介质中的传播,可以用Maxwell方程组来刻画。对于不同类型的材料,可以体现在方程本身的参数中,也可以体现在其方程所满足的边界上。我们希望可以不用实际物理实验就能对光在介质中的传播给出一些判断,比如说,光起作用的介质是什么形状的？为什么光和物质作用中主要是电磁波中的电矢量起作用？光与电磁波到底有什么关系？这些问题都可以通过求解所对应的数学模型给出结论,我们关心的就是这类具有实际物理意义的特征值问题[1]。总之，所有的探讨或是争论都是有意义的，它们推动了光学的发展，加深了人们对光本质的认知。现在普遍认为光具有波粒二相性[2]，而人们对光的认识还远远没有结束。随着计算机的快速发展，许多计算软件运用在各个学科领域，正是在这种趋势下MATLAB软件也被运用在光学的各方面研究之中。MATLAB是Matrix Laboratory(矩阵实验室)的简称，它在数学类科技应用软件中的数值计算方面首屈一指。MATLAB软件可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等，主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域,是一种用于算法开发、数据分析、数值计算以及数据可视化的高级技术计算语言[3]。

本文运用MATLAB软件的数值计算和仿真模拟功能，光的电磁理论推导反射、折射定律以及菲涅耳公式[4-9]，分析光在介质内传播特性的影响因子有入射角、介质折射率和入射光的波动特性；利用Matlab的强大数值计算与仿真功能[4]，计算模拟了光以不同入射角入射时的相关特性，得到了相关的特性曲线，并通过求解方程得到了振幅、相位和能流相对强度的变量函数关系，即电矢量的振动函数；最后分析计算机模拟结果与实验结论的符合程度[10-13]。

1 理论模型

光是横波，光射在两种介质的界面上时将发生反射和折射。能流的分配与入射角有关，还存在相位的跃变和偏振态的变化[5]。因此，根据平面波的横波特性，电矢量在垂直传播方向的平面内任意方向振动。可以分解成垂直于入射振动面和平行于入射振动面的分量。把垂直于入射振动面的分量称为s分量，把平行于入射振动面的分量称为p分量,如图1所示：

图1 s分量和p分量及其正反向规定

根据矢量点积运算性质，入射波、反射波和折射波的电场表达式，可得：

(1)

其中，m=s，p分别表示s分量和p分量，k1=2πn1/λ、k2=2πn2/λ。以下讨论s分量。

由反射定律得θi=θr，由折射定律得n1·sinθi=n2·sinθt，则：

k1·sinθi=k1·sinθr=k2·sinθt.

(2)

对光波振幅进行归一化处理，并令振幅反射系数rp=E0rp/E0ip，rs=E0rs/E0is，振幅透射系数tp=E0tp/E0ip，ts=E0ts/E0is。

利用式(2)，介质面边界条件可化为：

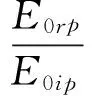
(3)

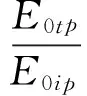
(4)

(5)

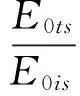
(6)

式(3)、(4)、(5)、(6)就是平面光波电矢量平行入射和垂直入射的菲涅耳公式[6]。其中式(3)、(4)是反射公式，式(5)、(6)是折射公式，各光波分量代表瞬时值。菲涅耳公式表明，反射、折射光波里的p分量只与入射光波里的p分量有关，s分量只与入射光波里的s分量有关。

由菲涅耳公式可以得到入射光、反射光和折射光的振幅关系与相位关系，现在进一步探讨三者之间的能流关系。假定光在传播过程中无吸收和散射无损耗，即总能量是保持不变的，以一束强度为Ii的平面光波入射到介质面上为例，当入射角为θi时，单位面积每秒的入射能量为：

(7)

式中ε1为介质1的介电常数，μ0为真空磁导率，θi为入射角。同理可得到相应的反射光和折射光的能量[1]：

(8)

(9)

对光波的能流也进行归一化处理，定义p分量和s分量的能流反射率分别为Rp=Wrp/Wip，Rs=Wrs/Wis，能流透射率分别为Tp=Wtp/Wip，Ts=Wts/Wis。根据能量守恒定律有Wrs+Wts=Wis，Wrp+Wtp=Wip。化简各分量反射与透射的关系式得：

(10)

综合以上探究可知：光的反射和折射特性主要取决于电矢量的振动情况，光在介质面的反射和折射特性主要由三个因素确定，分别是入射光的偏振态、介质折射率和入射角；以不同入射角入射时反射光和折射光的相位、振幅以及能流等特性发生相应变化。

2 数值计算与仿真模拟

2.1光疏介质进入光密介质的模拟计算

当光由光疏介质进入光密介质时，随着入射角的变化，反射光的振幅反射率、反射系数、强度以及透射光的振幅反射率、反射系数、强度均会发生变化。

2.1.1 振幅随入射角的变化特性

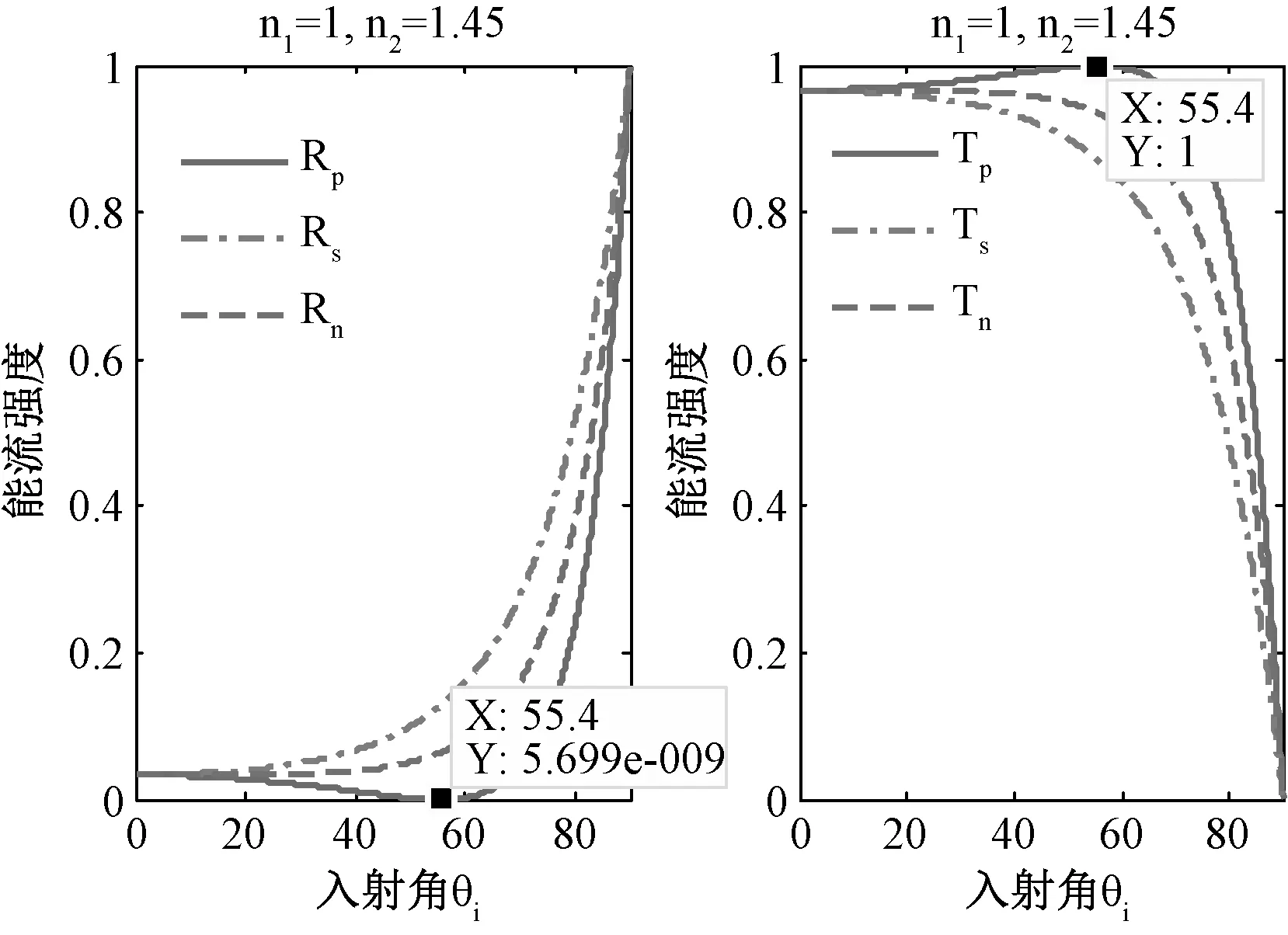
对于光由光疏介质传播到光密介质的情况，本文以入射介质折射率为1，透射介质折射率为1.45(如光由空气入射到石英玻璃)为例，根据介质面的边界条件，运用Matlab的数值计算和仿真模拟，得到了光由光疏介质传播到光密介质的振幅特性曲线，如图2所示：

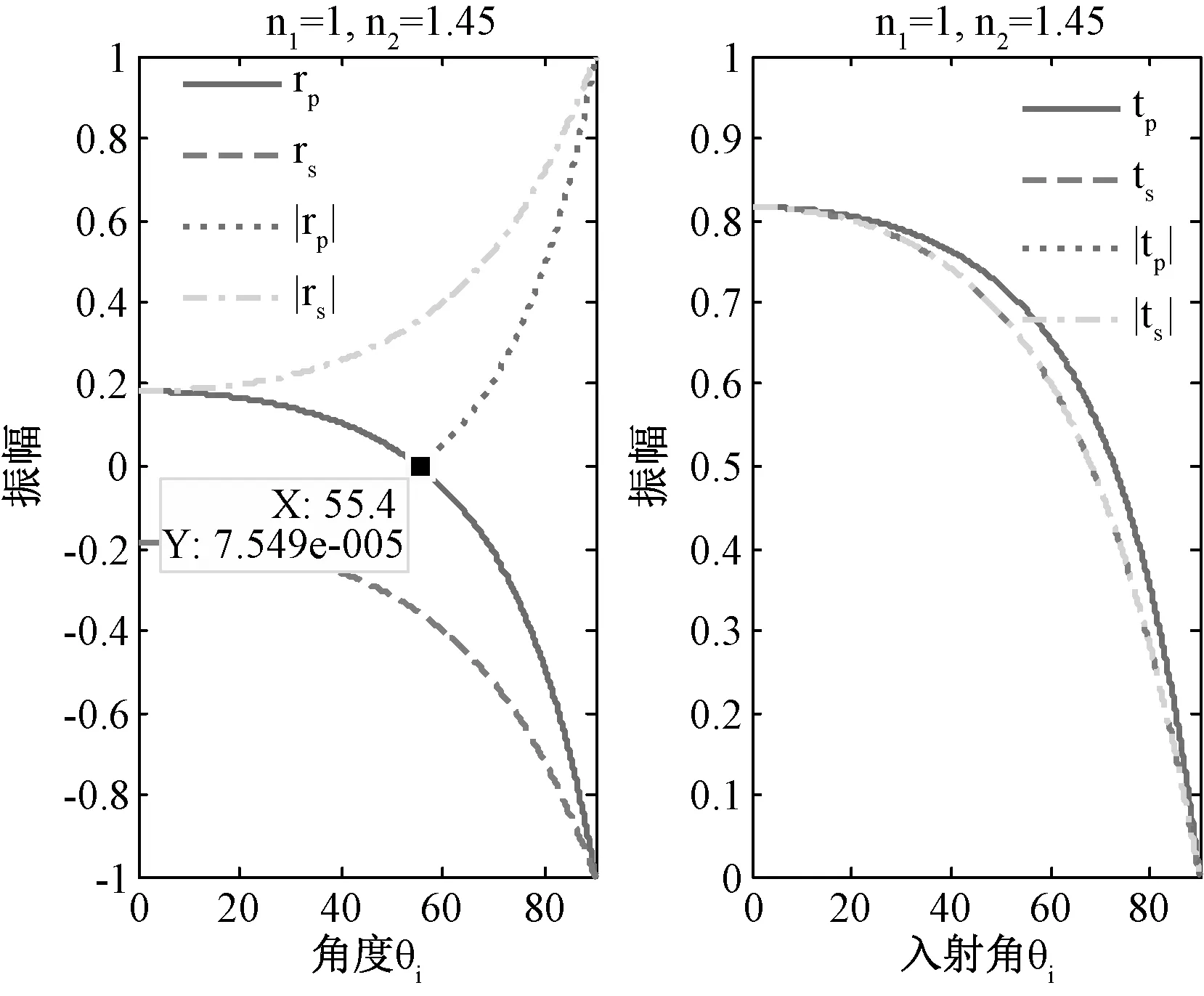
图2 光由光疏介质传播到光密介质的振幅特性曲线

由图2可以看出：当掠入射时，即入射角θi=90°时，rp=rs=1，tp=ts=0，表明此时没有折射光波，入射光全部被反射；当垂直入射即入射角度θi=0°时，rp，rs，tp，ts都不等于0，表明此时反射波和折射波同时存在。从图中还可以看出：|rs|随着入射角θi的增大而增大，|rp|随着入射角θi的增大而减小，当入射角θi达到一个特定值θB=55.4°时，|rp|=0，表明此时的反射光波中只有s分量而没有p分量，也就是产生全偏振现象，这个特殊角θB就是布儒斯特角，之后其随着入射角的增大不断增大，直到等于1；tp、ts随着入射角的增大而减小直到几乎为0。

2.1.2 相位特性

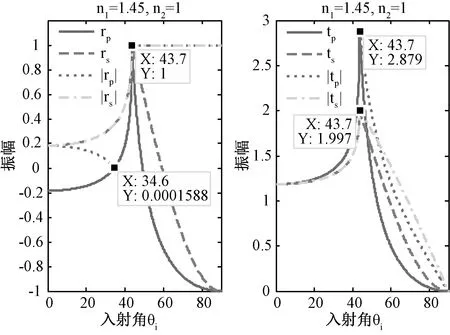
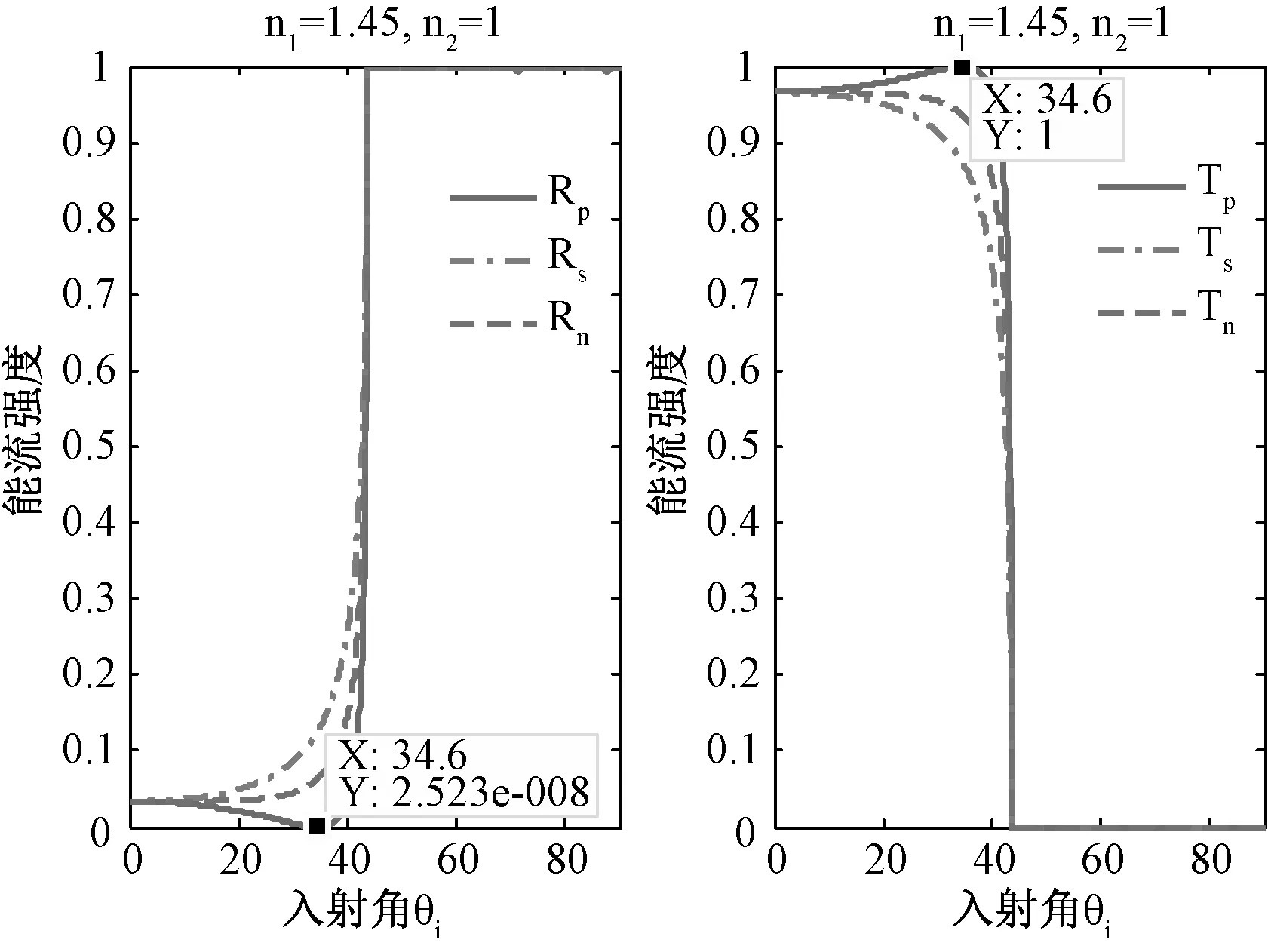
光由光疏介质进入光密介质时，由于n1

图3 光由光疏介质传播到光密介质的相位特性曲线

2.1.3 能流随入射角的变化特性

运用能流反射率、透射率公式(8)和(9)，计算了不同入射角度下的能流反射率和透射率，利用Matlab对反射光和透射光能流变化进行仿真模拟，结果如图4所示：

图4 光由光疏介质传播到光密介质的能流特性曲线

从图中可以看出：当垂直入射即入射角度θi=0°的情况下反射率和透射率Ts、Tp都不等于0，表明反射波和折射波同时存在；当掠入射即入射角度θi=90°的情况下，Rp=Rs=-1,Ts=Tp=0,表明此时没有透射光波，也就是发生了全反射现象。在图中还可以看出，随着入射角θi增大，Rs不断增加，Rp先减小直到入射角达到一特殊角θB时变为0，这个特殊角也即是布儒斯特角θB，而后又随着入射角的增大而增大。在整个过程中Ts和Rs变化相反，Tp和Rp变化也相反，始终有等式Ts+Rs=1、Tp+Rp=1恒成立。

2.2光密介质进入光疏介质的模拟计算

当光由光密介质进入光疏介质时，随着入射角的变化，反射光的振幅反射率、反射系数、强度以及透射光的振幅反射率、反射系数、强度同样会发生相应的变化，但可以预见由于全反射的存在，与3.1所探讨的光波由光疏介质进入光密介质的情况有所不同。

2.2.1 振幅随入射角的变化特性

根据介质面边界条件，运用Matlab的数值计算和仿真模拟，得到了光由光密介质传播到光疏介质的振幅特性曲线，如图5所示：

图5 光由光密介质传播到光疏介质的振幅特性曲线

由图可以看出：当垂直入射，即入射角θi=0°时各分量都不为0，表明反射波和折射波同时存在；对于反射光波中的p分量，|rp|随着入射角θi的增大而减小,直到入射角达到一特殊角时减为0，后又不断增大，直到入射角又达到一特殊角θC时变为1，这一特定角度即为全反射临界角。由图还可以看出：当入射角超过全反射临界角之后，rp、rs又不断减小，tp、ts也同样是减小，即透射与反射强度均减弱。但是由实验可知当入射角大于全反射临界角时，依旧发生全反射现象并不减弱[8]。

通过仿真计算可知：当入射角小于43.6°时rp、rs都是实数，当入射角为43.7°时开始出现虚数[9]。在Matlab中调用plot函数作图时对虚数只取实部，因此造成与实际情况不符。因此在入射角大于全反射临界角时，|rs|保持为1，rs不断减小直到-1。

2.2.2 相位特性

光由光密介质进入光疏介质时，当大于等于全反射临界角时发生全反射。为探讨区间的相位变化特性，利用菲涅耳公式计算得到的rp、rs在此区间为复数，再结合Matlab求复数辐角函数angle()，分别求出rp、rs和tp、ts，并得到了相位特性曲线，如图6所示[8]：

图6 光由光密介质传播到光疏介质的相位特性曲线

由图中可以看出：rp的相位在入射角小于θB=34.6°时为π，在θB到θC=43.6°保持为0,在发生全反射之后逐渐减为-π；rs、tp和ts的相位在发生全反射前保持为0，在全反射区间rs逐渐减为-π,tp和ts则逐渐减为-π/2。

2.2.3 能流随入射角的变化特性

根据2.1.3，同理可得到光由光密介质进入光疏介质时在界面上的能流变化情况，如图7所示：

图7 光由光密介质传播到光疏介质的能流特性曲线

由图中可以看出：当入射光垂直入射即入射角θi=0°时，Rs、Rp和Ts、Tp均不为0，表明反射光波和透射光波同时存在；随着入射角的增加，Rs同时增加且增加速度愈来愈大，Rp则先减小到0(此时入射角为一特定角)，随后又迅速上升到1；在此之后Rs、Rp始终保持为1。结合菲涅耳公式可知在全反射区间能流反射率保持为1，所有光波皆被反射回光密介质，在界面上无能量损失。

3 结论

基于MATLAB数值计算，物理光学理论和麦克斯韦电磁理论，运用理论推导的方法分别对不同边界条件下的波动方程、光的反射、折射定理和平面光波电矢量平行入射和垂直入射的菲涅耳公式等电矢量在介质表面的光传播特性做了研究。最后运用Matlab数据分析和作图功能，分别探究了光由光疏介质进入光密介质和由光密介质进入光疏介质两种情况下的光传播特性，并作出相应的光传播特性曲线。结果表明：光在介质面传播时会引起反射和折射现象，光的反射和折射特性主要取决于电矢量的振动；影响介质面反射、折射特性的因素主要是入射角、介质折射率和入射光的波动特性；光传播特性曲线能够直观简洁地展示光在介质面上传播的各种特性；光以不同入射角穿过两介质面时，反射光与折射光的相位、振幅以及能流等都会发生相应的变化。通过特性曲线还可直观地看出：光以布儒斯特角入射时发生全偏振现象；以大于临界角入射时发生全反射现象，发生全反射时能流透射率为0；随着入射角变化，反射光与透射光各分量相位发生突变或渐变，并因此造成半波段或整波段的损失。

[1]杨菁.物理光学模型中特征值问题的分析、计算及优化[D].杭州：浙江大学,2016:28-29.

[2]石顺祥.物理光学与应用光学[M].第2版.西安：西安电子科技大学出版社,2008:56-57.

[3]华初一.Matlab在光学教学及实验中的应用[D].呼和浩特：内蒙古大学,2013:17-20.

[4]欧攀,林志立,江洁.MATLAB数值计算在光学仿真和教学中的应用[J].教育教学论坛,2012(33):80-81.

[5]姚启钧.光学教程[M].第4版.北京：高等教育出版社,2008:43-48.

[6]蒲利春,姜毅.电磁矢量的菲涅耳公式[J].烟台师范学院学报(自然科学版),2005(2):126-129.

[7]魏仁怀,朱孟正.平面电磁波在运动介质界面上折射行为的研中[J].牡丹江师范学院学报(自然科学版),2009,69(4):10-12.

[8]徐诗池.电磁波“半波损失”的全面分析[J].上饶师范学院学报,2009,29(3):49-52.

[9]刘燕.电磁波在运动媒质表面的反射和折射[J].云南教育学院学报,1998,14(2):34-38.

[10]魏振博,王占山.光在非均匀介质中传播规律的演示[J].物理与工程,2014,24(3):34-36.

[11]高田桂.相对论与光在高速运动界面上的反射和折射[J].广西大学学报(自然科学版),1999,4(3):219-221.

[12]蔡新华.电磁波在运动媒质表面反射和折射时的多普勒频移[J].大学物理,1994,13(4):20-21.

[13]郑其明.基于折射定律的渐变介质中光传播路径研究及其应用[J].安徽师范大学学报(自然科学版),2015,38(3):245-249.

【责任编辑答会明】

NumericalCalculationonthePropagationCharacteristicsofLightBasedonMATLAB

ZHENG Xing-rong,SONG Xiao-yong,ZHENG Yan-fei,WANG Qi,JIANG Rong

(CollegeofElectricalEngineering,LongdongUniversity,Qingyang745000,Gansu)

O436.1；TP391.72

A

1674-1730(2017)05-0036-05

2016-12-16

陇东学院青年科技创新项目《轻惰性元素零点振动能的量子化学计算》(XYZK1501)

郑兴荣(1986—)，男，甘肃天水人，讲师，硕士，主要从事凝聚态理论物理与材料计算研究。