安装误差对面齿轮传动接触轨迹与接触应力的影响规律

陈书涵，高 洁，丁文强，严宏志，明兴祖

（1. 中国航发湖南动力机械研究所，湖南 株洲 412002；2. 中南大学 机电工程学院，湖南 长沙 410004；3. 长沙理工大学 汽车与机械工程学院，湖南 长沙 410114；4. 湖南工业大学 机械工程学院，湖南 株洲 412007）

安装误差对面齿轮传动接触轨迹与接触应力的影响规律

陈书涵1,2,3，高 洁1，丁文强1，严宏志2，明兴祖4

（1. 中国航发湖南动力机械研究所，湖南 株洲 412002；2. 中南大学 机电工程学院，湖南 长沙 410004；3. 长沙理工大学 汽车与机械工程学院，湖南 长沙 410114；4. 湖南工业大学 机械工程学院，湖南 株洲 412007）

基于面齿轮传动啮合原理，建立了含安装误差的面齿轮齿面方程，进而得出了面齿轮齿面主曲率及接触应力的计算方法。在此基础上，分别分析了轴向偏移误差、轴交角误差和轴交错误差对面齿轮传动的接触轨迹与接触应力的影响规律。研究结果表明：各项误差条件下，接触应力均从齿顶到齿根逐渐变小；所分析的误差中，轴交角误差与轴交错误差对面齿轮的接触轨迹与接触应力的影响较大，且当轴交角误差为负或轴交错误差为正时，接触应力仿真值均明显高于无误差时的接触应力正常值，因此在安装面齿轮副时，应该严格控制此二项误差的下上偏差。

面齿轮；安装误差；主曲率；接触应力

1 研究背景

长期以来，直升机主减速器的传动性能与可靠性、简化主减速器的结构、减轻其质量，一直是人们关注的重点[1]。在此情况下，寻找替代螺旋锥齿轮传动的面齿轮传动技术体现了其优越性，并逐步得到了广大科研人员的重视。面齿轮传动[2-3]是圆柱齿轮与一环形端面齿轮啮合构成的正交与非正交传动，两轴线正交的面齿轮传动如图1所示。

图1 正交面齿轮副示意图Fig. 1 Sketch of orthogonal surface gear pair

由于面齿轮传动具有传动平稳、动力分流效果好等优点[4-5]，因而受到了世界各国，尤其是西欧和北美等先进工业国家的重视，其早在20世纪后期就开始加快了对面齿轮传动的研究进程。如美国NASA（National Aeronautics and Space Administration）经过多年的实验研究，已将面齿轮传动技术应用到主减速器中，并且充分发挥了面齿轮传动的优越性，简化了其主减速器的结构与质量等。譬如美国的ART（the Advanced Rotorcraft Transmission）计划中，波音公司生产的阿柏奇战斗直升机应用了面齿轮副(如图2所示)，以其代替原来的弧齿锥齿轮传动结构[6]，这一改进使得齿轮箱的总成质量减轻了40%，但承载能力提高了35%，并节省了大量空间。

图2 ART计划的面齿轮分扭传动Fig. 2 Torque-split transmission of face gears with ART plan

在面齿轮接触应力的研究方面，已有研究主要集中在有限元分析方法上。如F. L. Litvin等[7]运用TCA（tooth contact analysis）理论，并结合有限元分析及实验验证，获得了面齿轮不同啮合位置的接触应力及随啮合位置的分布规律。韦贤玕[8]应用有限元方法分析了面齿轮多齿啮合周期中5个不同啮合状态下的接触应力，并获得了面齿轮多齿啮合下接触应力的分布规律。刘艳平[9]采用有限元分析方法，对面齿轮多齿模型进行了LTCA分析，获得了不同载荷条件对面齿轮接触应力、弯曲应力等传动性能的影响规律。严宏志等[10]考虑表面粗糙度的影响，对面齿轮齿面接触应力进行了分析。

本研究拟从正交面齿轮传动设计出发，针对面齿轮的安装误差，分析其对面齿轮副传动在传动过程中啮合点处接触应力的变化规律，以期为面齿轮副的安装提供理论参考依据。

2 建立含安装误差的面齿轮齿面方程

按照图1所示面齿轮副建立正交面齿轮的安装坐标系，如图3所示。

图3 正交面齿轮传动中安装坐标系与安装误差示意图Fig. 3 Schematic diagram of installation coordinate and installation error of orthogonal surface gear transmission

图3中δp为轴向偏移误差，δγm为轴交角误差，δa为轴交错误差，这3种误差统称为正交面齿轮的安装误差。

假设Sf为无安装误差时的坐标系，Sf′为有安装误差的坐标系。根据齐次坐标转换原理可得由Sf′坐标系变换成Sf坐标系的变换矩阵Mff′为

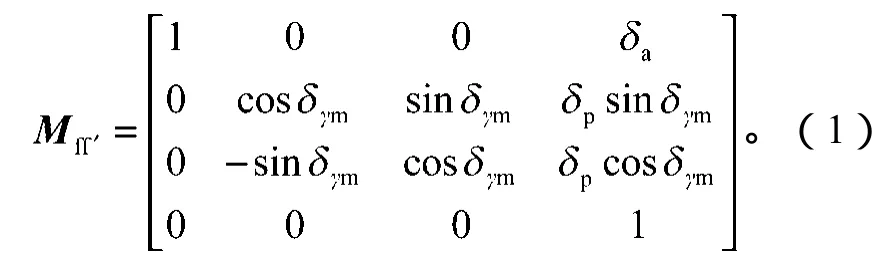
Ag1为S1动坐标系变换至Sg固定坐标系的矩阵，且；

r1为圆柱齿面方程；

rb1为圆柱齿轮基圆半径；

u1为圆柱齿面上一点沿Z1方向的轴向参数；

n1为单位法向量；

Lg1为Ag1的子矩阵（去掉最后一行与一列）。

点接触正交齿轮传动的原理如图4所示。

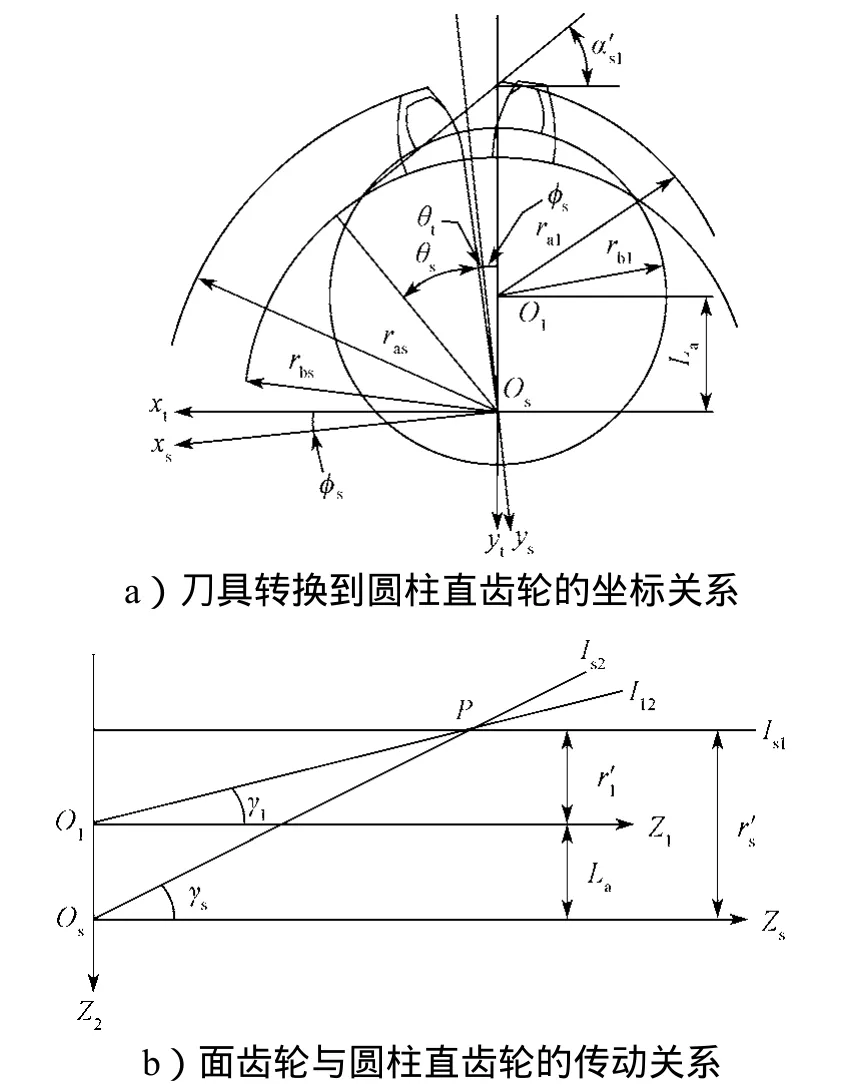
图4 点接触正交面齿轮传动原理图Fig. 4 Schematic diagram of point contact orthogonal face gear transmission

图4所示原理图中，αs1′为啮合角，θs为插齿刀具渐开线函数，θt为插齿刀具齿槽对称线到渐开线起点的角度参数；ra1为圆柱齿轮齿顶圆半径，rb1为圆柱齿轮基圆半径，ras为插齿刀具齿顶圆半径，rbs为插齿刀具基圆半径，s为圆柱齿轮齿槽对称线到渐开线起点的角度参数，La为插齿刀具到圆柱齿轮的中心距；γ1为圆柱齿轮节锥角，γs为插齿刀具节锥角，Is1为插齿刀具与圆柱齿轮的瞬时接触线，Is2为插齿刀具与面齿轮的瞬时接触线，I12为圆柱齿轮与圆柱齿轮的瞬时接触线，P为节点，r′1为圆柱齿轮节圆半径，r′s为插齿刀具节圆半径。

由图4所示点接触正交齿轮传动原理图，可得在节点P的u1为

另外，考虑安装误差，由坐标系S2至坐标系Sg的转换矩阵Ag2为

根据坐标系的齐次变换关系，可得rg(2)和ng(2)的方程为

利用式（2）（3）（9），可获得含安装误差的面齿轮接触轨迹方程如下：

3 面齿轮齿面接触点主曲率与接触应力计算

根据弹性力学理论，对于任意形状的两个曲面接触点的主曲率，都与接触点的接触应力与变形大小有关，因此需要对接触点的主曲率进行计算。

根据参考文献[11]，设一曲面的参数方程为

式中：E、F、G为Ⅰ类量，L、M、N为Ⅱ类量，且E=ruru；F=rurv；G=rvrv；L=-nuru=ruun；M=-nurv=ruvn；N=-nvrv=rvvn。

由微分几何知，主曲率的计算公式为

由公式（14）可以看出，主曲率的计算存在着两个不同的根，即曲面上一点存在着两个不同主曲率，而且主方向相互垂直。

因此，在计算圆柱直齿轮主曲率K11、K12与面齿轮主曲率K21、K22时，只要把圆柱直齿轮与面齿轮的齿面方程分别按照上述步骤进行计算即可。

另外，根据赫兹接触理论，得到面齿轮接触点的最大接触应力公式为

式中：a为接触椭圆的长轴半径；b为接触椭圆的短轴半径；P1为接触点的法向作用力。其中a、b可通过式（16）计算得出，P1可通过式（18）计算得出。

式（16）中：α、β、ζ为椭圆计算系数，查表并线性插值可得；

E1、E2为弹性模量；

μ1、μ2为泊松比；

A、B为关于接触曲面主曲率的方程，且

其中，T为齿轮传动的负载扭矩，Rb1为小轮（圆柱直齿轮）的基圆半径。

4 安装误差对面齿轮接触点接触轨迹与接触应力的影响

4.1 安装误差对面齿轮接触轨迹的影响

根据前文得到的方程（10），运用Matlab进行编程计算，分别对上述3种安装误差对接触轨迹的影响进行仿真分析，所得仿真结果如图5所示。设计的基本参数如下：小齿轮齿数N1=23；面齿轮齿数N2=125；模数m=6.35 mm；压力角α=20º；弹性模量E1=E2= 2.06×105MPa；泊松比μ1=μ2=0.30；载荷为负载扭矩T=42 N·m。

图5 当考虑安装误差影响时的接触轨迹仿真图Fig. 5 Contact trajectory simulation diagram with the installation error considered

对图5进行分析可知：

1）当轴交角误差δγm为正时，接触轨迹沿着面齿轮的大端发生位移；当轴交角误差δγm为负时，接触轨迹沿着面齿轮的小端发生位移。

2）当轴交错误差δa为正时，接触轨迹沿着面齿轮的小端发生位移；当轴交错误差δa为负时，接触轨迹沿着面齿轮的大端发生位移。但是相对来说，接触轨迹的运动在这3种类型的误差影响中是最小的。因此，点接触面齿轮传动的齿面接触轨迹对轴交错误差相对不敏感。

3）当轴向偏移误差δp为正时，接触轨迹沿着面齿轮的大端发生位移；当轴向偏移误差δp为负时，接触轨迹沿着面齿轮的小端发生位移。

综上所述，在装配面齿轮传动时，对轴交角误差δγm要严格要求。

4.2 接触应力影响分析

根据上述面齿轮参数，编制Matlab程序对式（16）进行面齿轮长短轴a、b值计算，进而根据式（15）得到接触点的接触应力，所得仿真结果如图6～8所示。

图6 轴交角误差影响时的接触应力图Fig. 6 Contact force under the in fl uence of intersection angle error

图7 轴交错误差影响时的接触应力图Fig. 7 Contact stress of the axis staggered error

图8 轴向偏移误差影响时的接触应力图Fig. 8 Contact stress of the axial deviation error

分析图6～8，可以得到以下结论：

1）由于接触点从齿顶逐渐向齿根位置移动时，它的椭圆长轴与短轴是逐渐增大的，因而从图6～8可知，齿面接触应力是由齿顶向齿根逐渐变小的。

2）由图6可知，当轴交角误差取正或取负时，接触应力都要偏离无轴交角误差时的接触应力，而且这种偏离随着接触点往齿根移动而逐渐变小。当误差为正时，接触应力少于正常的接触应力；当误差为负时，接触应力大于正常的接触应力，此时对面齿轮传动的接触强度有影响。

3）由图7可知，当轴交错误差取正或取负时，接触应力都要偏离无轴交角误差时的接触应力，而且这种偏离随着接触点往齿根方向移动而逐渐变小。当误差为负时，接触应力小于正常的接触应力；当误差为正，接触应力大于正常的接触应力，此时对面齿轮传动的接触强度有影响。

4）由图8可知，当轴向偏移误差取正或取负时，对齿面接触应力的影响相对较小，且当轴向偏移误差为负时，影响更小。

综上所述，从这3项误差影响接触应力的大小来看：轴向偏移误差影响最小，轴交错误差影响次之，轴交角误差影响最为显著。

5 结论

本文从安装误差的角度出发，分析了轴向偏移误差、轴交角误差和轴交错误差对面齿轮的接触轨迹及接触应力的影响，由仿真结果可以得知：

1）轴交角误差与轴交错误差对面齿轮的接触轨迹与接触应力的影响相对较轴向偏移误差的大，因此在面齿轮安装时，应该严格控制轴交角误差的下偏差及轴交错误差的上偏差。

2）不考虑安装误差时，由仿真结果可知，接触应力在齿顶的位置最大，这是因为在此位置容易发生齿顶边缘接触。且选择的3项误差影响接触应力的大小为轴向偏移误差影响最小，轴交错误差影响次之，轴交角误差影响最为显著。

综上，本研究为面齿轮的安装及对安装误差的控制提供了理论依据。

[1]王 志，刘建炜，刘 锐，等. 面齿轮传动的国内研究进展[J]. 机械设计与制造，2012(3)：219-221.WANG Zhi，LIU Jianwei，LIU Rui，et al. The Domestic Research Progress of Face Gear Transmission[J].Machinery Design and Manufacture， 2012(3)：219-221.

[2]HANDSCHUH R，LEWICKI D，BOSSLER R.Experiment Testing of Prototype Face Gears for Helicopter Transmissions[R]. Solihull：NASA.TM-105434，1992.

[3]LITVIN F L， ZHANG Y， WANG J C，et al.Design and Geometry of Face-Gear Drive[J]. Journal of Mechanical Design，1992 ，114(4)：642-647.

[4]DENG G，KATO M，MARUYAMA N，et al. Initial Temperature Evaluation for Flash Temperature Index of Gear Tooth[J]. Journal of Tribology，1995，117(3)：476-481.

[5]HANDSCHUH R F. Thermal Behavior of Spiral Bevel Gears[D]. Cleveland：Case Western Reserve University，1993.

[6]LITVIN F L，IGNACIO G P，ALFONSO F，et al.Design，Generation and Stress Analysis of Face-Gear Drive with Helical Pinion[J]. Computer Methods in Applied Mechanics & Engineering，2005，194(36)：3870-3901.

[7]LITVIN F L，EGELJA A，TAN J，et al. Computerized Design，Generation and Simulation of Meshing of Orthogonal Offset Face-Gear Drive with a Spur Involute Pinion with Localized Bearing Contact[J]. Mechanism and Machine Theory，1998，33(1/2)：87-102.

[8]韦贤玕. 正交面齿轮传动几何计算及强度分析[D]. 哈尔滨：哈尔滨工业大学， 2016.WEI Xiangan. Geometric Calculation and Strength Analysis of Orthogonal Face Gear Drive[D]. Harbin：Harbin Institute of Technology，2016.

[9]刘艳平. 直齿-面齿轮加载接触分析及弯曲应力和接触应力计算方法研究[D]. 长沙：中南大学，2012.LIU Yanping. Study on the Loading Contact Analysis and Bending Stress and Contact Stress Calculation Method of the Straight Teeth-Face Gear[D]. Changsha：Central South University，2012.

[10]严宏志，胡 威，何国旗. 考虑表面粗糙度的面齿轮齿面接触应力分析[J]. 机械设计与研究，2012，28(4)：58-65.YAN Hongzhi，HU Wei，HE Guoqi. Contact Stress Analysis of Face-Gear Drive with Considering the Surface Roughness[J]. Machine Design and Research，2012，28(4)：58-65.

[11]李瑰贤.空间几何建模与工程应用[M].北京：高等教育出版社，2007：11-17.LI Guixian. Space Geometry Modeling and Engineering Applications[M]. Beijing：Higher Education Press，2007：11-17.

(责任编辑：廖友媛)

In fl uence of Installation Errors on Contact Trajectory and Contact Stress of Face Gear Drive

CHEN Shuhan1,2,3，GAO Jie1，DING Wenqiang1，YAN Hongzhi2，MING Xingzu4
（1. Hunan Power Machinery Research Institute of China’s Aviation Engine Group，Zhuzhou Hunan 412002，China；2. School of Mechanical and Electrical Engineering，Central South University，Changsha 410004，China；3. School of Automobile and Mechanical Engineering， Changsha University of Technology，Changsha 410114，China；4. School of Mechanical Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China）

Based on the meshing principle of face gear drive, a surface equation has been established of the face gear with the installation error, thus obtaining the calculation method of the main curvature and contact stress of the tooth surface of face gear. On this basis, a respective analysis has been made of the in fl uence of axial deviation error, axial angle error and axial staggered error on the contact trajectory and contact stress of the face gear drive. The results show that the contact stress decreases gradually from the addendum to the root under various error conditions.According to the error analysis, the shaft angle error and axial across error are the most important in fl uential factors on the contact trajectory and contact stress of the face gear, when the angle error is negative or axis error is positive in its value, the contact stress simulation values are signi fi cantly higher than those normal contact stress without errors.Therefore, it is highly recommended that the upper and lower deviation of these two errors be strictly controlled when installing the face gear pair.

face gear；installation error；main curvature；contact stress

TP215

A

1673-9833(2017)04-0008-06

10.3969/j.issn.1673-9833.2017.04.002

2017-06-02

国家自然科学基金资助项目（51575533，51375161），湖南省自然科学基金资助项目（2017JJ4023）

陈书涵（1977-），男，湖南衡阳人，长沙理工大学讲师，中国航发湖南动力机械研究所传动中心博士后，主要研究方向为面齿轮传动强度设计，E-mail：29094680@qq.com