强声波作用下烟气夹带单颗粒煤粉传热特性的数值研究
许伟龙, 姜根山, 安连锁, 刘月超
(1.华北电力大学 能源动力与机械工程学院,北京 102206;2.华北电力大学 数理系,河北保定 071003)
强声波作用下烟气夹带单颗粒煤粉传热特性的数值研究
许伟龙1,2, 姜根山2, 安连锁1, 刘月超1,2
(1.华北电力大学 能源动力与机械工程学院,北京 102206;2.华北电力大学 数理系,河北保定 071003)
根据二维轴对称、非稳态、层流的质量、动量和能量守恒方程,研究了强声波作用下夹带在烟气中单颗粒煤粉的传热特性.分析了声压级为145~167 dB,频率f分别为50 Hz、1 000 Hz和5 000 Hz时,颗粒壁面的温度场、局部努塞尔数、表面平均努塞尔数及时间-空间平均努塞尔数的分布.结果表明:当f=50 Hz时,颗粒壁面流场主要受到曲率效应的影响,努塞尔数随着振荡速度幅值的增大而增大;随着频率的增大,流动加速度的作用逐渐加强,当f=5 000 Hz时,热边界层与流场之间出现了相位迟滞;不同频率时颗粒的努塞尔数相差不大,时间-空间平均努塞尔数的最大差值比为2.82%;当声压级为167 dB,f=5 000 Hz时,颗粒的时间-空间平均努塞尔数是无声场时的1.78倍.
强声波; 传热特性; 局部努塞尔数; 表面平均努塞尔数; 时间-空间平均努塞尔数; 相位迟滞
Abstract: Heat transfer characteristics around single coal particles entrained by flue gas under the action of high intensity acoustic field were studied based on two-dimensional, unsteady and laminar equations for mass, momentum and energy conservation and transport, so as to analyze the temperature field, local Nusselt, surface-averaged Nusselt and space- and time-averaged Nusselt numbers around the coal particles at the sound pressure level (SPL) varying in 145-167 dB and at frequencies of 50 Hz, 1 000 Hz and 5 000 Hz, respectively. Results show that at 50 Hz, the flow field around coal particles is mainly affected by curvature effects, and the Nusselt number increases with the rise of amplitude of oscillation velocity; with the rise of frequency, the effect of flow acceleration increases, and phase lag would appear between the thermal boundary layer and the oscillating flow field at 5 000 Hz; the combined effects of curvature and flow acceleration result in the maximum difference of 2.82% in the space- and time-averaged Nusselt number at different frequencies, i.e. little difference of Nusselt number; the space- and time-averaged Nusselt number is 1.78 times of that without acoustic field at 167 dB and 5 000 Hz.
Key words: high intensity acoustic wave; heat transfer characteristics; local Nusselt number; surface-averaged Nusselt number; space- and time-averaged Nusselt number; phase lag
在电站锅炉中,煤粉高效燃烧主要通过3种途径来实现:(1)强化煤粉气流的传热传质;(2)提高煤粉的高浓度聚集;(3)强化燃烧的初始阶段.近年来大量研究表明,振荡流体中固体的传热传质率明显增强.在工程应用上这一现象受到了广泛的关注和研究,如强化燃烧[1-2]、干燥[3]以及强化管道换热[4]等.实验证明,煤颗粒在强声波形成的振荡流中燃烧时,燃烧时间明显缩短,有效地提高了燃煤率[5].与机械振荡流不同,强声波驱动下的振荡流不但具有大振幅的特性,同时还有声流等次级效应.
在气固两相流、固定床及流化床等涉及到颗粒流的场合下,要分析整个过程的传热情况首先需要对单颗粒的传热特性有正确的理解,继而将单颗粒的传热特性与气体流动关联起来,可对整个过程的传热情况进行可靠的分析和计算[6].单个球形颗粒和液滴在振荡流场中的传热传质研究最早是在20世纪40年代,Marthelli等[7]对单一球形颗粒和小球滴燃料燃烧时热量和质量传输随振荡流场的变化进行了探索.Ranz等[8]通过理论推导和实验分析,提出了稳流中单颗粒在不同条件下的传热传质计算公式,这一结果被研究者们广泛接受,并应用于实际工业计算和相关数值模拟计算中.Sayegh等[9]研究了环境为空气时的传热传质现象,提出了振荡流中单颗粒的传热传质计算公式.Ha等[10]采用数值计算方法计算了二维非稳态气相层流质量、动量及能量守恒方程,给出了无叠加稳态项的时态方程下不同振荡流时颗粒表面速度场和温度场.何雅玲等[11]对脉动流动强化凸块散热进行了数值研究,分析了雷诺数Re、斯特劳哈尔数Sr和脉动振幅A等参数对凸块散热性能和通道中压力损失的影响.Hossein等采用实验方法研究了频率为25 kHz的超声波声场中铜球的传热特性,并分析了普朗特数Pr和声强等参数对传热系数的影响.
根据目前的文献,已有部分针对振荡流中单颗粒或液滴传热传质特性的研究.然而,这些研究大多数为实验研究,对于振荡流中单颗粒或液滴传热传质特性的机理研究很少.基于炉内高温负压环境,笔者采用数值计算方法建立并求解了球坐标系下的二维非稳态、层流的动量、质量及能量守恒方程,分析了强声波作用下炉内单颗粒煤粉的传热特性,并讨论了局部努塞尔数、表面平均努塞尔数及时间-空间平均努塞尔数随声压级和频率变化的分布规律,为进一步研究强声波强化煤颗粒燃烧提供了理论基础.
1 物理模型与控制方程
1.1 物理模型与控制方程
煤粉是由不规则形状的微细颗粒组成的颗粒群,颗粒在炉膛中由于碰撞、温差等因素会影响其传热特性.为了简化研究,主要对单个颗粒的传热特性进行了分析,将煤颗粒近似为球体,颗粒夹带在烟气气流中,颗粒相对于烟气处于静止状态,物理模型如图1所示,其中T0为烟气温度,Tp为颗粒温度,U1为声质点振荡速度的幅值,f为声频率,t为时间,r为颗粒外某点与球心之间的距离,θ为此点和球心的连线与轴之间的夹角.模型圆周对称并以穿过颗粒中心且与流动方向平行的线为轴,图1中所示变量沿着切向和径向变化.炉内压力p0=101 225 Pa(负压为100 Pa),烟气温度T0=1 000 ℃,颗粒温度Tp=1 400 ℃,用于计算流体物性的定性温度为1 200 ℃.
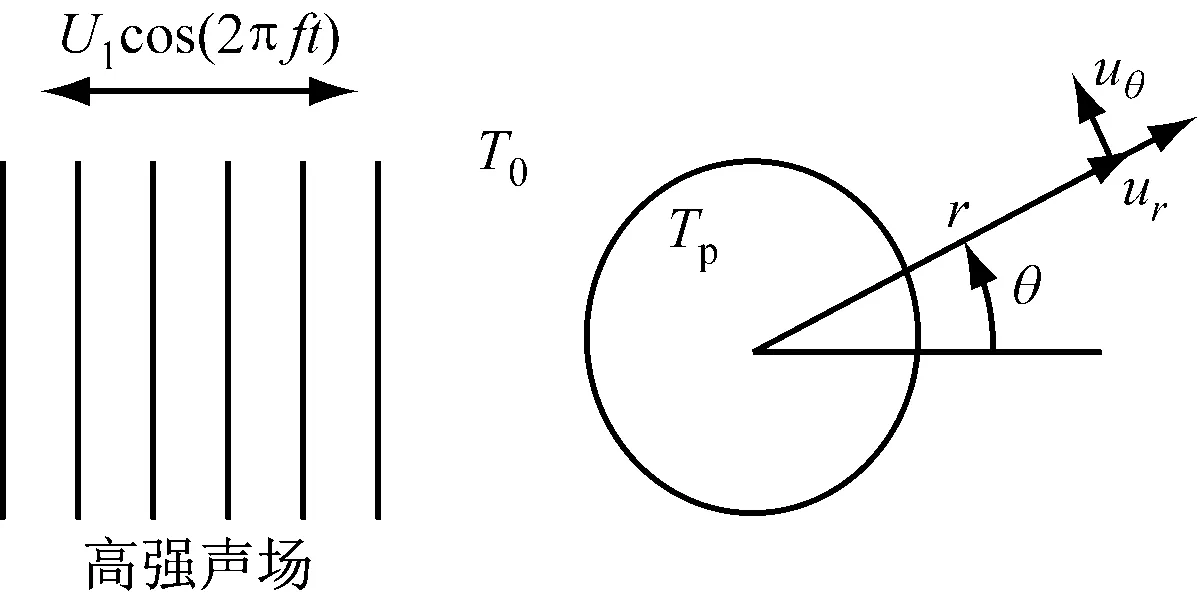
图1 高强声波作用下振荡流绕球形颗粒流动及流场变量分布示意图
1.2 控制方程
在球坐标系下,二维轴对称、非稳态、常物性、无内热源、层流的质量、动量及能量守恒的通用微分方程[12]如下:
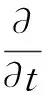
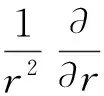
(1)
式中:φ=ur,ur、uθ和e分别为径向速度、轴向速度和内能;Sφ为源项,见表1,其中p为压强,λ为流体的导热系数;μ为流体的动力黏度;cp为比定压热容;ρ为流体密度;Γφ为影响变量的特性参数.

表1 式(1)中源项Sφ的表达式
2 数值计算
2.1 无量纲数
炉内颗粒与烟气之间的稳定滑移速度为U0,其雷诺数定义为:
Re0=U0D/ν
(2)
式中:D为颗粒的粒径;ν为烟气的运动黏度.
强声波作用于颗粒时,声雷诺数定义为:
Re1=U1D/ν
(3)
斯特劳哈尔数定义为:
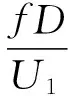
(4)
颗粒壁面局部努塞尔数Nuθ定义为:
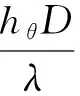
(5)
式中:hθ为颗粒壁面局部传热系数;Tsph为温度;R为颗粒半径.
沿着轴向对局部努塞尔数Nuθ进行积分运算,得到表面平均努塞尔数Nus:

(6)
经过几个周期的运算时间后,程序达到准静态状态,不同周期内的表面平均努塞尔数Nus分布相同.时间-空间平均努塞尔数可表示为:

(7)
式中:T为声振动周期.
2.2 边界条件及网格划分
控制方程式(1)的初始条件及边界条件[10]分别如下:
初始条件,t=0时,
φ=φ0
(8)
边界条件,t>0时,θ=0及θ=π时(轴对称条件),

(9)
当r=R时,
φ=φp
(10)
且离球心无穷远处,即r→∞时,
(11)
式中:φp为颗粒表面独立变量φ的值;由于颗粒相对于烟气静止,表面无滑移,因此颗粒表面径向速度urp及轴向速度uθp均为0.
电站锅炉炉膛中煤粉颗粒粒径在100 μm左右,本文中取颗粒粒径为100 μm,计算区域为颗粒粒径的10倍区域,计算模型如图2所示.模型中计算区域采用有限差分格式进行离散,沿着θ角,在切向划分为360等分,沿着径向,划分为50等分.算法采用SIMPLEC算法.根据文献[5]中的方法,对模型进行了正确性验证.
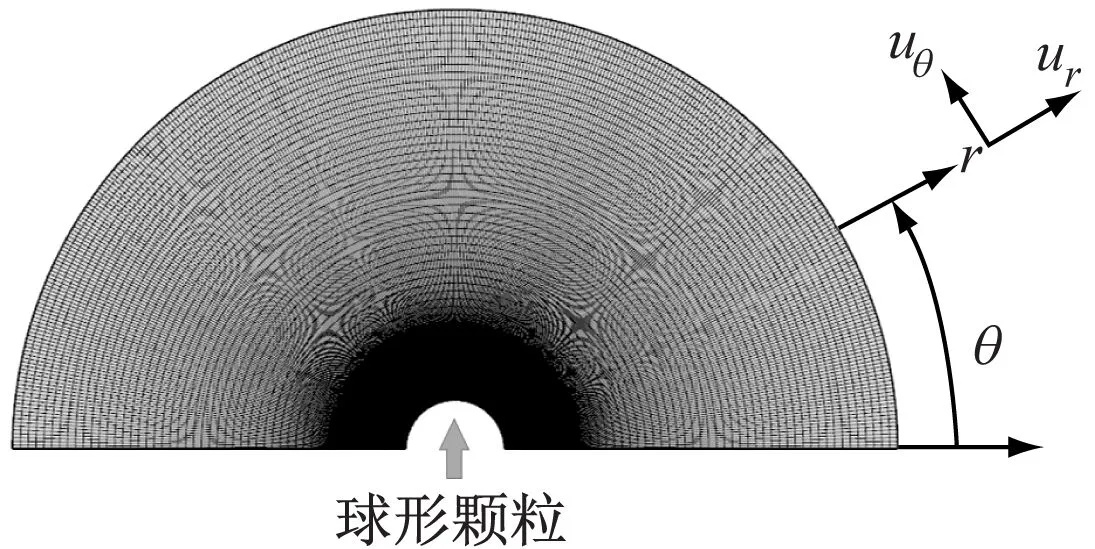
图2 模型坐标系及计算网格
2.3 物性参数
当有一列平面波射入炉膛时,有效声压为prms,声阻抗为ρgC0(其中ρg为烟气密度,kg/m3;C0为炉膛中声速,m/s),则声质点振荡速度振幅U1为:

(12)
式中:prms=10A,A=(Lp-94)/20,Lp为声压级.

3 计算结果与分析
图3和图4为声压级为157 dB,声雷诺数Re1=4.98 (U1=11 m/s),稳流雷诺数Re0=0,频率f分别为50 Hz (Sr=4.55×10-4)和5 000 Hz (Sr=4.55×10-2)时,计算区域内颗粒表面的等温线分布.图中所示等温线代表无量纲过余温度(Tsph-T0)/(Tp-T0).在τ=0T(τ=f·t,τ表示一个稳定周期内不同的时间点)时,由于振荡速度呈余弦形式变化,此时方向从左至右,沿着颗粒表面θ从90°至180°,等温线分布越密,温度梯度越大.而在τ=0.375T时,由于振荡速度方向改变,沿着θ从90°至0°等温线分布越来越密.

表2 炉膛压力为101 225 Pa时烟气的热物理性质

(a)τ=0T(b)τ=0.125T(c)τ=0.25T(d)τ=0.375T(e)τ=0.5T(f)τ=0.625T(g)τ=0.75T(h)τ=0.825T
图3 强声波声压级为157 dB,频率为50 Hz时颗粒在不同时刻的等温线分布
Fig.3 Isothermal lines around a spherical particle at 157 dB and 50 Hz in high intensity acoustic field

(a)τ=0T(b)τ=0.125T(c)τ=0.25T(d)τ=0.375T(e)τ=0.5T(f)τ=0.625T(g)τ=0.75T(h)τ=0.825T
图4 强声波声压级为157 dB,频率为5 000 Hz时颗粒在不同时刻的等温线分布
Fig.4 Isothermal lines around a spherical particle at 157 dB and 5 000 Hz in high intensity acoustic field
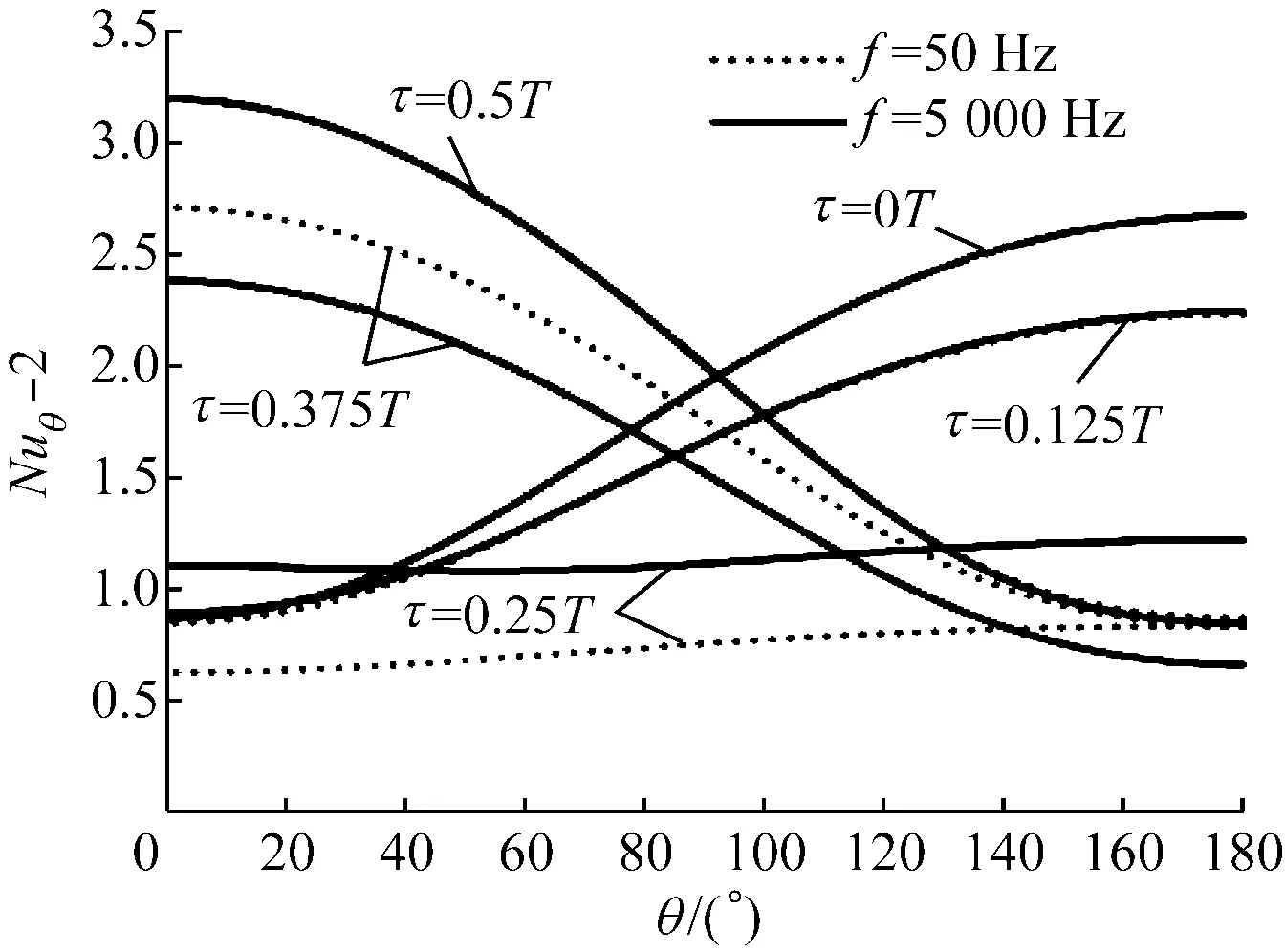
图5给出了声压级为157 dB,Re1=4.98,Re0=0,f分别为50 Hz和5 000 Hz时,不同时刻局部努塞尔数Nuθ在颗粒壁面的分布.由于Nuθ=2时,颗粒表面的换热形式仅为热传导,为了区分对流与热传导,图5纵坐标选为Nuθ-2.由图5可知,由于颗粒壁面不同点的温度梯度不同,各点的Nuθ也不一致,且振荡速度呈余弦形式变化;在不同时刻,颗粒壁面的Nuθ也不相同.在τ=0T~0.25T,θ=180°处Nuθ出现最大值;在τ=0T,f=50 Hz时,Nuθ最大值为3.568;当f=5 000 Hz时,Nuθ最大值为3.483.在τ=0T~0.25T,随着振荡速度幅值不断减小,Nuθ不断减小;在τ=0.25T,f=50 Hz时Nuθ最大值为2.817,f=5 000 Hz时Nuθ最大值减小为3.09.
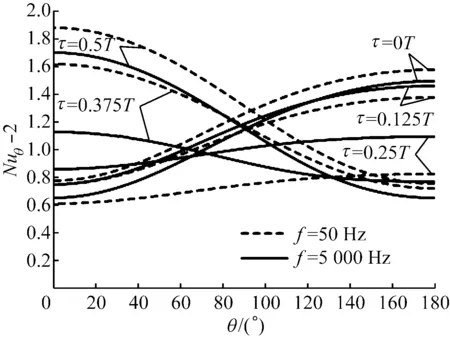
图5 声压级为157 dB,频率为50 Hz和5 000 Hz的强声波声场中不同时刻Nuθ沿颗粒表面角度变化的分布
Fig.5 Distribution ofNuθon surface of a particle at 157 dB, 50 Hz and 5 000 Hz, respectively, in high intensity acoustic field
在τ=0.25T~0.5T,由于振荡速度方向发生变化 (即从右至左),在θ=0°处Nuθ出现最大值.在这个时段随着振荡速度幅值的增大,Nuθ增大;在τ=0.5T,低频时Nuθ最大值为3.873,高频时Nuθ最大值为3.694.可以发现在τ=0.5T时,无论低频还是高频,Nuθ最大值均大于τ=0T时的Nuθ最大值.根据Ha等[13]的研究,振荡流中物体在振荡速度为负最大值时,Nus要大于振荡速度为正最大值时的Nus,本文计算结果与其吻合.与一般振荡流不同,强声波除了具有大振幅特性外,在其作用下颗粒表面会形成一个独立的稳定流动,与振荡流的速度、方向无关,即为声流.声流的形成导致在τ=0T和τ=0.5T时Nuθ最大值出现微小差别.
在τ=0.5T~0.75T和τ=0.75T~T,外部势流的流动速度与流动加速度的幅值分别与τ=0T~0.25T和τ=0.25T~0.5T时相同,只是方向相反.因此,Nuθ-2在τ=0.5T~0.75T和τ=0.75T~T时的分布特性分别与在τ=0T~0.25T和τ=0.25T~0.5T时的分布相似,但曲线均为反对称关系.
由于颗粒表面形成一个与外部声场无关的稳定流场,热边界层与声场之间可能会形成相位迟滞.振荡流的特征时间尺度tch,f为:
tch,f=1/ω
(13)
式中:ω为角频率,当f=50 Hz时,tch,f=3.18 ms;而当f=5 000 Hz时,tch,f=0.031 8 ms.
动量交换的特征时间尺度为:
tch,h=δh/Urms
(14)
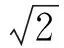
传热的特征时间尺度tch,f为:
tch,T=δT/Urms
(15)
式中:δT为热边界层厚度.
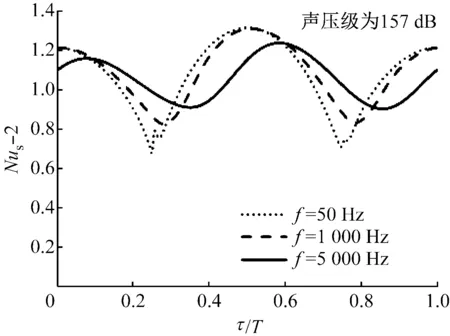
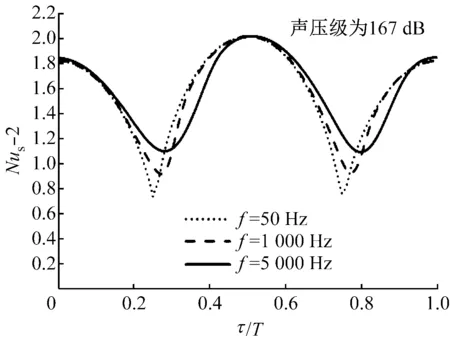
烟气的普朗特数Pr=0.56,因此热边界层厚度与流动边界层厚度几乎相同.当tch,T< 相比于频率,振荡速度是影响热边界层响应的特征时间的最重要因素.由于,响应时间主要受到惯性力和黏滞力的作用,随着声压级的增大,振荡速度增大,响应时间减小.然而外部势流的特征时间更多的是受到频率的影响.为了计算传热的近似特征时间量,将颗粒壁面θ=90°的点沿着径向与无量纲过余温度为(Tsph-T0)/(Tp-T0)=0.01时等温线的距离定义为热边界层厚度δT.当声压级为157 dB,f=50 Hz,τ=0T、τ=0.25T及τ=0.5T时,tch,f分别为0.039 2 ms、0.050 8 ms及0.037 7 ms,在这种情况下,tch,T< 当声压级由157 dB增至167 dB,Re1由4.98增至15.75时,流动边界层厚度不断减小,颗粒壁面处温度梯度变得更为陡峭,传热效率增强.图6和图7给出了声压级为167 dB,Re1=15.75 (U1=34.8 m/s),Re0=0,f分别为50 Hz (Sr=1.44×10-4)和5 000 Hz (Sr=1.44×10-2)时,计算区域内颗粒表面的等温线分布.当f=50 Hz,τ=0T、τ=0.25T及τ=0.5T时tch,f分别为0.006 27 ms,0.015 96 ms及0.005 66 ms,此时tch,T< (a)τ=0T(b)τ=0.125T(c)τ=0.25T(d)τ=0.375T(e)τ=0.5T(f)τ=0.625T(g)τ=0.75T(h)τ=0.825T 图6 强声波声压级为167 dB,频率为50 Hz时颗粒在不同时刻的等温线分布 图7 强声波声压级为167 dB,频率为5 000 Hz时颗粒在不同时刻的等温线分布 Fig.7 Isothermal lines around the spherical particle at 167 dB and 5 000 Hz in high intensity acoustic field 图8 声压级为167 dB、频率分别为50 Hz和5 000 Hz的强声波声场中不同时刻Nuθ沿颗粒表面角度变化的分布 Fig.8 Angular variation ofNuθaround a particle at 167 dB, 50 Hz and 5 000 Hz, respectively, in high intensity acoustic field 根据式(9)计算得到颗粒的Nus.图9给出了f=50 Hz,Re0=0, 声压级为145~167 dB (Re1=1.25~15.75)时,颗粒在一个周期内的Nus分布.由图9可知,随着声压级的增大,Nus增大.这主要是因为随着声压级的增大,Re1增大,颗粒表面的速度梯度变得陡峭,进而导致温度梯度增大.图中出现的极大值点与极小值点分别对应着振荡速度最大值与最小值. 图9 颗粒Nus的分布 图10给出了声压级为145~167 dB,Re0=0,Re1=1.25~15.75时,不同频率时颗粒在一个周期内的Nus分布.由上文可知,随着频率的增大,声场与热边界层之间的相位迟滞逐渐产生并增大.当声压级为157 dB,f=50 Hz时,Nus-2的极大值在τ=0T和τ=0.5T时出现,分别为1.21和1.31;Nus-2的极小值在τ=0.25T和τ=0.75T时出现,分别为0.68和0.71,此时振荡速度的幅值为0.当f增至5 000 Hz时,Nus-2的极大值在τ=0.08T和τ=0.585T时出现,分别为1.16和1.23;而Nus-2的极小值在τ=0.35T和τ=0.855T时出现,分别为0.91和0.9.频率不同时,极大值与极小值出现的时间点不同,表明存在相位迟滞.同时也可以发现相同声压级时,随着频率的增大,Nus-2极小值的数值越大,这是因为随着频率的增大,颗粒周围流场的分布由受到曲率效应和振荡速度影响变为同时受到曲率效应、振荡速度和流动加速度的影响,频率越大,颗粒壁面周围流动分离的现象越严重,形成的涡越多,对流场扰动也越大,因此在图10中可以看到Nus-2极小值数值的增大.当U0=0 m/s时,对于稳定流绕颗粒运动,Nus-2=0,然而对于声场驱动下的振荡流绕颗粒运动,当振荡速度幅值为0时,Nus-2>0,除了相位滞后的原因外,颗粒壁面所发生的流动分离与声流效应也起到了一定作用. 当声压级为167 dB,f=50 Hz时,tch,T< (a) (b) (c) (d) 根据式(7)计算得到颗粒的Nut.文献[8]中的单颗粒传热计算公式为: (16) 文献[9]中给出的适用于空气介质的单颗粒传热计算公式为: (17) 式(16)和式(17)的适用条件均为tch,T< 图11给出了声压级为145~167 dB,Re1=1.25~15.75,不同频率时Nut-2的值以及由式(16)、式(17)所得Nut-2的值.由图11可知,模拟计算值要大于机械振荡流绕颗粒经验公式所得的值,这主要是由于在强声波作用下声流效应的产生以及低雷诺数下颗粒壁面流动分离的发生、涡的形成扰动了颗粒壁面的流场,增大了表面温度梯度,进而增大了努塞尔数.当Re1=1.25、4.98和9.05,f=1 000 Hz时,Nut-2的值最大;而当Re1=15.75时,随着频率的增大,Nut-2的值增大.其中,Re1=1.25,f=1 000 Hz时Nut-2的值与f=5 000 Hz时Nut-2的值存在最大差值比,比率为2.82%.当声压级为167 dB时,Nut=3.56,是无声场时的1.78倍,颗粒的传热效率增强了近一倍. 图11 不同声雷诺数时Nut-2的值 (1)随着声压级的增大,颗粒的努塞尔数增大,传热效率增强. (2)当频率分别为50 Hz、1 000 Hz和5 000 Hz时,颗粒的努塞尔数相差不大,Nut-2的最大差值比为2.82%.在流动分离现象与相位滞后的共同作用下,努塞尔数并不随着频率的增大而单一增大. (3)当声压级为167 dB时,颗粒的Nut是无声场时的1.78倍,颗粒的传热效率得到了增强. (4)为强化煤颗粒与烟气之间的传热,应尽量增大强声波的声压级. [1] JIANG Genshan, ZHENG Yinchao, PAN Jie, et al. The enhancement of pulverized-coal combustion by using sound waves[J].TheJournaloftheAcousticalSocietyofAmerica, 2012, 131(4): 3468. [2] 王瀛洲,韩璞. 声场强化煤粉燃烧的试验研究[J].动力工程学报, 2014, 34(4): 271-274. WANG Yingzhou, HAN Pu. Research on boiler combustion enhancement by sound field[J].JournalofChineseSocietyofPowerEngineering, 2014, 34(4): 271-274. [3] KIANI H, SUN D W, ZHANG Z. Effects of processing parameters on the convective heat transfer rate during ultrasound assisted low temperature immersion treatment of a stationary sphere[J].JournalofFoodEngineering, 2013, 115(3): 384-390. [4] DHANALAKSHMI N P, NAGARAJAN R, SIVA-GAMINATHAN N, et al. Acoustic enhancement of heat transfer in furnace tubes[J].ChemicalEngineeringandProcessing:ProcessIntensification, 2012, 59: 36-42. [5] HA M Y, KIM S M. Combustion of a single droplet in the presence of an oscillating flow[J].KSMEJournal, 1995, 9(2): 209-224. [6] 虞君武, 何榕. 张衍国. 分形颗粒在低Reynolds数条件下传热特性[J].清华大学学报(自然科学版), 2014, 54(6): 781-786, 798. YU Junwu, HE Rong, ZHANG Yanguo. Heat transfer characteristics of a fractal particle in a low Reynolds number flow[J].JournalofTsinghuaUniversity(ScienceandTechnology), 2014, 54(6): 781-786, 798. [7] MARTHELLI R C, BOELTER L M K. The effect of vibration on heat transfer by free convection from a horizontal cylinder[C]//Proceedings5thInternationalCongressofAppliedMechanics. USA: MIT, 1939, 578-584. [8] RANZ W E, MARSHALL W R. Evaporation from drops, part I and part II[J].ChemicalEngineeringProgress, 1952, 48(3): 173-179. [9] SAYEGH N N, GAUVIN G D. Numerical analysis of variable property heat transfer to a single sphere in high temperature surroundings[J].AIChEJournal, 1979, 25(3): 522-534. [10] HA M Y, YAVUKURT S, KIM K C. Heat transfer past particles entrained in an oscillating flow with and without a steady velocity[J].InternationalJournalofHeatandMassTransfer, 1993, 36(4): 949-959. [11] 何雅玲, 杨卫卫, 赵春凤, 等. 脉动流动强化换热的数值研究[J].工程热物理学报, 2005, 26(3): 495-497. HE Yaling, YANG Weiwei, ZHAO Chunfeng, et al. Numerical study of enhancing heat transfer by pulsating flow[J].JournalofEngineeringThermophysics, 2005, 26(3): 495-497. [12] HA M Y. A theoretical study of augmentation of particle combustion via aocusitc enhancement of heat and mass transfer[D]. Pennsylvania, USA: The Pennsylvania State University, 1990. [13] HA M Y, YAVUKURT S. A theoretical investigation of acoustic enhancement of heat and mass transfer-II. Oscillating flow with a steady velocity component[J].InternationalJournalofHeatandMassTransfer, 1993, 36(8): 2193-2202. Heat Transfer Characteristics Around Single Coal Particles Entrained by Flue Gas Under the Action of High Intensity Acoustic Field XUWeilong1,2,JIANGGenshan2,ANLiansuo1,LIUYuechao1,2 (1. School of Energy, Power and Mechanical Engineering, North China Electric Power University,Beijing 102206, China; 2. Department of Mathematics and Physics, North China Electric Power University, Baoding 071003, Hebei Province, China) 2016-09-29 2016-12-20 国家自然科学基金资助项目(11474091, 11674093, 11274111);河北省自然科学基金资助项目(A2015502077) 许伟龙(1988-),男,湖北荆门人,博士研究生,主要从事声波在炉内的传播特性及声效应方面的研究. 姜根山(通信作者),男,教授,博士生导师,电话(Tel.):13603229460;E-mail:gsjiang@ncepu.edu.cn. 1674-7607(2017)10-0788-08 TK124 A 470.30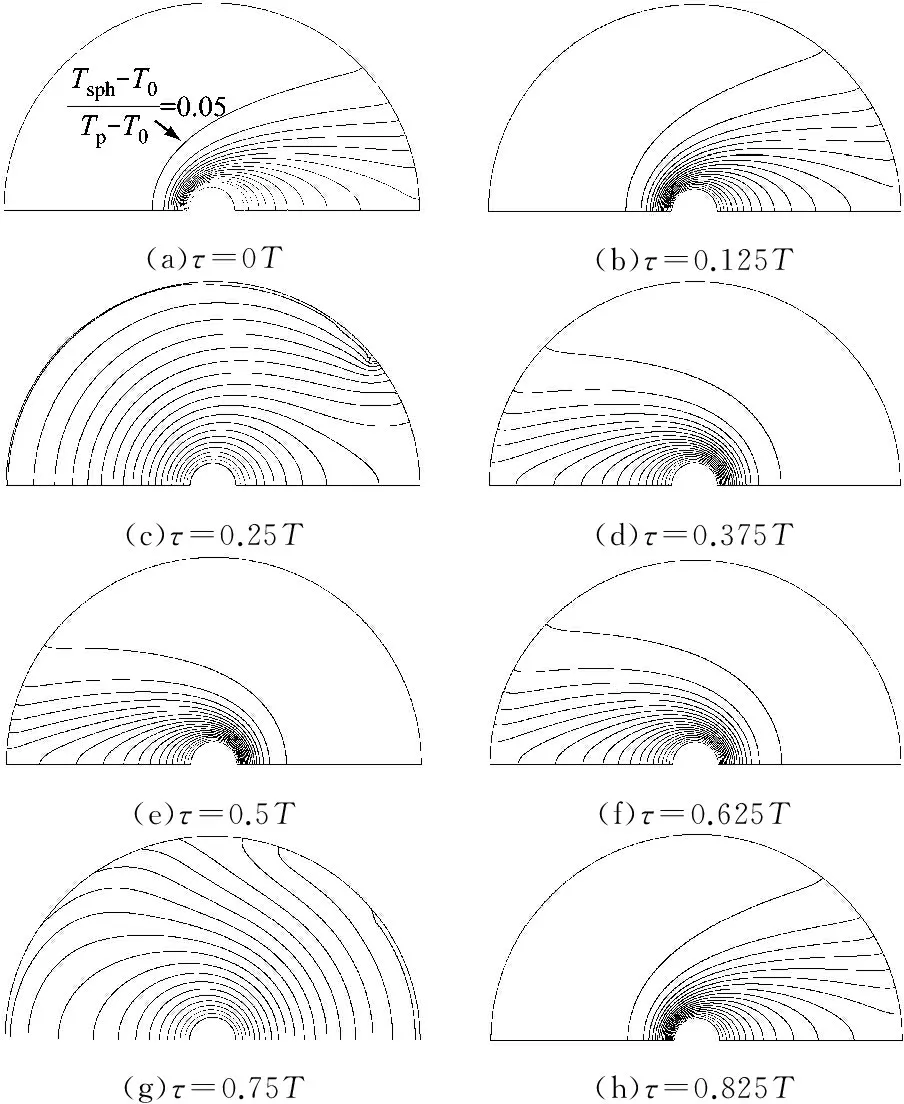



4 结 论

