基于空间填充曲线排列码划分的并行缓冲区算法
申金鑫,吴 烨,陈 荦,景 宁
(国防科技大学 电子科学与工程学院, 湖南 长沙 410073)
0 引 言
进入大数据时代,空间数据呈现“爆炸式”增长,对现有计算资源及分析方法造成了巨大挑战。OSM(OpenStreetMap)全球道路网数据已经达到了1亿条以上,且在不断完善更新。因此,传统分析计算和架构在应对这样日趋海量、日益复杂的空间数据时已经越来越“捉襟见肘”。相较之下,依托日益成熟的并行技术的高性能计算方法日益显露出优越性,得到广泛关注。
矢量缓冲区分析确定近邻度,是GIS空间分析中的一个重要的基本功能,应用广泛[1]。如计算通信基站覆盖范围、河流水患影响区域、公共交通服务保障面积等。
在矢量数据缓冲区生成算法研究方面,很多工作基于平行双线算法。文献[2-5]针对平行双线算法遇到的特定问题进行了改进。此外,文献[6-7]分别使用边约束三角网辅助法和缓冲区方程近似描述方法提高了缓冲区生成效率。但是,这些方法大多基于单机串行进行,应对更大规模的海量数据时性能提升有限。
并行计算方法研究方面。制定并行计算策略主要考虑数据划分和任务分解两方面问题,因而在并行缓冲区分析应用中,计算流程可以分为数据划分、任务分解、缓冲区计算、缓冲区合并等流程,且已有一些相关研究。
文献[8]主要聚焦数据划分以及空间聚集特性保持,提出了基于图层和地理空间区域的任务分解方法,在网格环境下实现了缓冲区的并行计算,但容易导致子任务间粒度差异大。
文献[9-10]针对并行计算中任务划分和合并的问题,基于MPI提出了基于节点数量的任务划分和二叉树任务合并的优化方法。此外,文献[11]通过裁剪算法将单条数据切分成多个几何部件,而后进行合并得到该对象的缓冲区范围。但是,这两种方法在任务划分时都没有涉及数据空间聚集特性的保持。
文献[11]着重考虑了数据任务分解过程中的负载均衡,根据线面数据的复杂性特点,在集群环境下,利用MPI和GRASSGIS实现了等弧段分解任务,但是在保持空间关系以及更大规模数据集的执行效率等方面还有待验证。
基于此,综合考虑并行优化方法,得到以下研究思路。首先,保持空间数据邻近关系,在此基础上进行划分数据,同时避免数据倾斜问题;然后,合理分解数据块,保持负载均衡;最后,结果合并时,设计调度方法充分利用并行计算资源。
由于MPI模型多进程编程较复杂,在可扩展的并行缓冲区计算上存在瓶颈[10]。近年来,MapReduce、Spark等大数据处理框架,以其良好可扩展性、高效迭代等优点提升了数据处理效率。虽然这些框架本身不支持对空间数据的处理,但在其基础上,各种空间数据处理方法不断提出并完善。如GeoSpark[12]提供了SRDD,支持kNN和空间连接操作,并且能够添加网格和R树索引。此外还有SpatialSpark[13]和Simba[14]等。上述系统支持很多基本的空间操作,但并没有针对缓冲区计算等基本的空间分析功能进行设计与改进。
本文以分布式内存计算框架为基础,结合整体计算流程提出了一种基于空间填充曲线排列码进行数据划分的并行缓冲区分析算法(SPBM,SFC-based Partition Buffer Method)。本文的主要工作如下:
1)引入空间填充曲线排列码对空间矢量对象划分,进一步提出了一种基于Hilbert编码的自适应的划分方法,为了应对边界相交问题,针对线矢量数据提出了一种近似切割的空间数据划分策略;
2)在基于数据点数量的任务分解方法基础上,采取了设定深度参数下的“树状”结果合并方法。
3)在一系列真实数据集上,与多种缓冲区分析方法进行单机和集群环境下的对比实验,验证了本文方法的有效性。
1 问题描述
空间矢量数据可以表示为集合D={di|i=1,2,…,N},其中d表示单个矢量对象,N表示数据集总数量。集粗粒度下,缓冲区分析可以表示为描述为Fs(D,r),如式(1),其中,Fs表示串行计算映射函数,输入包括数据D和缓冲区距离r。就属性而言,可以分为两个步骤,单个对象缓冲区计算Fbuffer,和缓冲区合并Funion。
在并行计算时,如式(2),数据划分成了p份,可以描述为Fp(D,r,p),其中,Fp表示并行计算映射函数,计算过程中数据被分成了p块。并行计算中,显而易见,Fbuffer不涉及节点间通信,但是如何将D分布到c个计算节点上需要考虑以下3个问题:
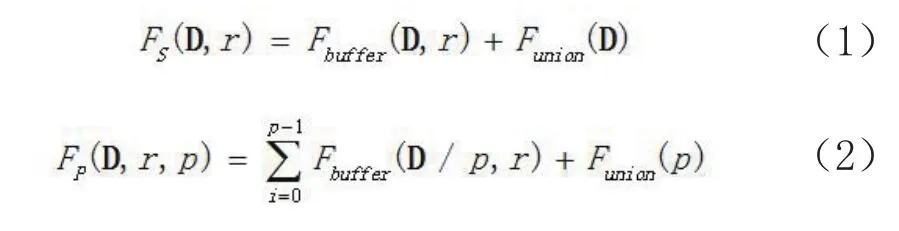
问题1:空间数据聚集性
数据分块后,D→{Di|i=1,2,…,p},数据块Di对应的缓冲区计算结果Gi空间重叠应当尽量小,否则后续Funion开销很大。因此,需要按照空间属性来进行二维划分。应当满足条件:空间上邻近的数据划分到相同的Di中。
问题2:切分数据块合理性
Di应当花费大致相同计算时间,否则会造成阻塞。现实情况却是,实际矢量数据空间分布不均衡,线、面数据长度len(d)不一,按照对象数量的分解方式效果不佳。优化方法应当包含:①数据倾斜处理,避免出现单条大数据;②负载均衡考虑,单个Di的计算量以及p与c的合理配置。
问题3:结果合并并行化
Funion合并应当避免串行方式,否则会“滚雪球”方式不能充分利用资源。
2 基于区域划分的并行矢量缓冲区分析算法
缓冲区分析算法可以分成数据划分、边界数据处理、任务分解,以及结果合并等几个步骤,如图1所示。数据读入后,进行空间填充曲线数据划分,得到〈Sc,d〉形式的数据,其中,Sc是空间填充曲线编码值;按照Sc排序,即可体现聚集特性。然后,对跨越网格的数据进行切分处理,避免出现单条大数据。之后,根据输入数据总数据量N对数据进行分解,得到数据量分别为B1,B2,…,Bi(i∈[1,p])的子任务D1,D2,…,Di,使得B1,B2,…,Bi基本相等,以避免出现负载不均衡的问题。最后,进行结果合并,由于串行的方法将导致计算过程中的等待,本文采用指定归并树深度的“树状”归并方法,将每个Di计算得到的结果Gi(i∈[1,p])逐级归并,最终将结果输出。
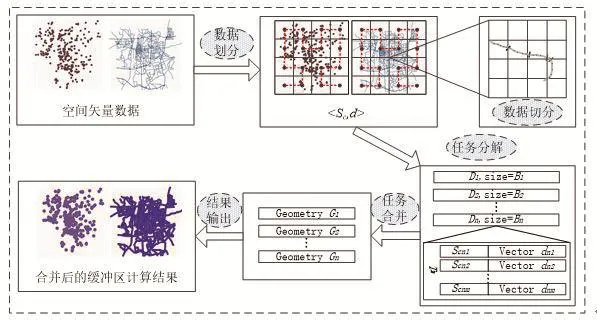
图1 基于区域划分的并行矢量缓冲区分析算法框架图Fig.1 Flow chart of parallel vector buあer analysis algorithm based on region partitionc
2.1 基于空间填充曲线的数据划分
在并行计算时,需尽可能保证空间聚类特性,避免将空间相邻的数据分配到不同的计算节点上,以此来减少网络开销。空间填充曲线在保持空间邻近特性方面有着无可比拟的优点,包含Hilbert曲线、Z-order曲线等,其中Hilbert曲线的空间邻近性更好[15-16]。本文基于Faloutsos[17]等提出的Hilbert曲线编码生成算法对空间数据进行数据划分。按照Hilbert曲线划分排序后,可以保持空间聚集特性,为后续任务分解过程提供组织模式,为缓冲区合并过程减少了拓扑判断开销。文献[10]表明,基于Hilbert编码的数据划分方法是其并行缓冲区优化算法尚待继续研究的问题。
在选定空间填充曲线的类型SFC基础上,需要设定合理的空间曲线层级Li。Li设定的目标是每个网格内的数据量差异不会太大,以缓解数据倾斜问题带来的影响。为了针对不同分布特征的数据集得到最佳的空间填充曲线层级,本文提出了一种基于空间填充曲线编码的自适应数据划分算法。最终的算法描述如算法1。
算法1.基于空间填充曲线编码的自适应数据划分算法.
输入:初始输入空间矢量数据,空间填充曲线SFC,初始选定层级Lk,阈值Tsc;
输出:空间填充曲线层级k.
for (l=k) do
根据k,按SFC算法生成填充曲线
if (data.type=POINT)
根据公式(2)计算Scki
else if (data.type=LINE)
拆分数据为多个X&Y坐标对Vij(j∈[1,len(Di)]),按公式(2)分别计算Sckij
end if
对得到的〈Scki,Di〉按不重复的Scki(i∈[1,m])分为m组
统计Scki对应的数据量Ti
if (max(Ti)>Tsc)
k=k+1
else
输出结果
end if
end for
2.2 边界数据切分
在划分过程中,不可避免地遇到跨越网格的d,为了避免这些数据因为遗漏而造成结果错误,需要对在网格边界上的点和线数据采取不同的处理方式。当前并行分布式计算方法中,主要有指定网格法和复制法两种处理方法[18]。本文对点矢量数据采用指定网格方法。然而,实际线矢量数据长度差异明显,且存在单条长矢量数据,跨越多个网格。基于此,指定网格法无法避免单条长d造成的数据倾斜问题;复制法既不能解决数据倾斜问题,而且会带来计算量的增长。即便采取按照网格边界切分法,这需要考虑到线d与多个网格的拓扑关系,计算复杂度大。因此,结合之前Hilbert编码网格划分方式,本文采取一种近似切分方式。
线矢量数据近似切分。通过几何部件划分合并的方式可以得到单个对象的缓冲区范围[10],进一步,可按照网格在单条线数据的节点处进行切分,并为每一条新得到的数据计算其对应的编码值Sc。这样大的数据就分解成了对应多个网格的多条数据,从而进一步破解计算瓶颈,得到总数量为M的新数据。算法描述如算法2。设定一个不切分数据的阈值F,在顺序计算各个节点Sc时,从Sc变化的节点进行切割。为了保持最终计算结果的正确性,分割节点既是上一条数据的终点,又是下一条数据的起点。
算法2.线矢量数据近似切分算法.
输入:输入空间数据di(i∈[1,N]),空间SFC的层级k;
输出:处理完边界问题后的〈Sci,di〉(i∈[1,M])数据对.
按照k生成SFC
for each di
计算数据长度len(di)
if (len(di)<F)/* F对一般实际空间数据设为3即可*/
Sci=OF(Vij|j=[ F/2]), 输出〈Sci,di〉
else
for Vijin di
if (OF(Vij)!= OF(Vi(j-1)))
在Vij处切割,得到切割数据dix/*Vij既是切割数据终点,又是原数据起点*/
Scix=OF(Vi(j-1)), 输出〈Scix,dix〉/*切分得到的数据对应一个SFC编码值*/
end if
end for
end if
end for
2.3 给定深度“树状”结果合并
空间缓冲区分析中,最后的步骤就是缓冲区计算结果的合并,先将d的单个缓冲区求出,后将其全部合并得到最终结果。该步骤与2.2节之间还有任务分解过程,本文对切分后数据按照均匀节点方法进行分解。
并行计算过程中,Funion合并需要考虑相互的空间位置和拓扑关系,涉及到大量网络传输开销,因而合并任务的调度成为一个性能提升的瓶颈。树状合并方法能够起到优化作用,使得计算复杂度由O(p)降为了O(logp)。文献[9-10]中均采取的是二叉树类似的进程合并方式,在2z个进程(z∈[1,5])的情况下验证了优化效果。不同于进程合并,本文从数据块树状合并的角度出发,使用了给定深度树状缓冲区合并方法。输入给定深度参数h,按照该参数进行近似“树状”任务合并。如图2所示,首先,D1…D6先计算出数据块中数据的缓冲区及其合并结果,得到数据块的缓冲区计算结果集G1…G6。然后,根据给定的深度h开始树状归并。由于给定深度的合并方法减少了合并过程中的数据块数量,减少了网络传输开销,因而起到了明显的优化效果。
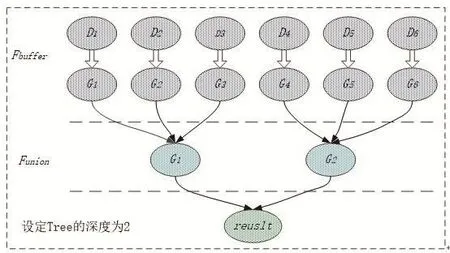
图2 给定深度“树状”结果合并示例Fig.2 Example of tree-like task combination with given depth
3 实验与分析
3.1 实验设置
在本节中,分别在单机和集群两种不同环境下进行了实验。代码用Scala语言实现。实验基于Spark1.6.1,Hadoop2.6,Java1.8_101;QGIS版本为2.0;PostGIS版本为2.1;CitusData版本为5.2(是对PostGIS的集群扩展)。实验硬件环境见表1。

表1 实验环境Tab.1 Experiment environment
实验使用了点、线等实际数据,其中线要素最大规模达到了60万量级。数据汇总见表2。考虑更大规模的数据集的计算结果十分复杂,对前端可视化造成巨大压力,当前实际应用效果有限,因而并未进行相关实验。其中,P1和P2是兴趣点数据;L1是城市道路数据,长度比较均衡;L2是地区道路数据,较L1包含了更多单条长数据,由节点数量对比也可看出;L3与L2为同一地区,是该地区更全面的数据集;L4是国家道路网数据集。

表2 实验使用的数据集Tab.2 Datasets used in the experiment
3.2 实验结果对比分析
实验1至实验3验证算法影响因素,并说明本文方法的科学性,在单机中进行;实验4是算法对比实验,分别在单机和集群环境中进行,以验证SPBM的高效性和可扩展性。所有实验中,缓冲区距离r设置为200 m。
实验1 网格划分方式对比实验
为验证空间填充曲线划分方法带来的性能提升,对无划分方法(No Partition,NP)、普通网格的划分方法(Grid Partition,GP)、Z曲线编码网格划分方法(Z-curve Partition,ZP)以及本文采取的Hilbert曲线编码网格划分方法(Hilbert-curve Partition,HP)等4种方法进行了对比,其中,NP、GP以及HP方法采用相同的网格生成方法。为了隔离数据切分等优化措施的影响,因而没有采用线矢量数据集进行实验,而是基于点矢量数据集P1和P2。由表3可知,3种网格划分方法相较于NP都实现了很高的加速比。就GP、ZP和HP而言,HP方法因为空间邻近性更好而效率略高。在P2数据集上,由于数据密集带来数据块内实际计算量增长,因而3种方法加速比下降。

表3 数据划分方法对比实验结果Tab.3 Experiments on data partition methods.
为验证自适应空间填充曲线层级设定的必要性,在P2数据集上进行空间填充曲线层级影响实验。见表4,3种方法都受曲线层级的影响,趋势大致相同,随曲线层级增加,计算效率先显著增加,然后稍微下降。当层级过低,单个网格中的数据量过多,划分不能起到相应的效果,曲线层级L=11和L=12的实验结果相比,单个网格中最大数据量显著降低,因而更好的空间聚集特性使得平均加速比达到了6.21。当层级过高,划分过密,反而增大了计算量,不会起到性能提升作用。
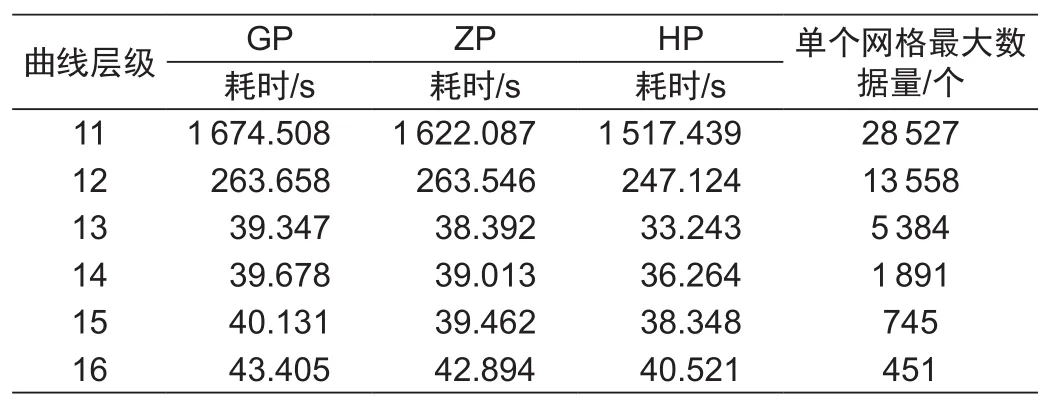
表4 曲线层级对实验结果影响Tab.4 Experiments on diあerent layers of SFC curve
实验2 跨网格数据处理方法对比实验
本实验对无网格划分法(No Partition,NP)、指定网格法(Selected Copy,SC)、以及本文采用的近似切分法(Approximate Split,AS)3种方法进行比较。由于复制法相较于指定网格方法而言复杂度更高,因此未参与比较。
实验结果见表5。在较小数据集L1测试时,SC和AS较NP处理效率高。但是由于城市道路网数据长度比较均衡,因而SC和AS间差距并不明显。当处理包含更多单条长数据的L2时,AS带来的性能提升十分明显,较SC实现了12.2的加速比。由于SC已经按照其中间的节点得到了编码值SC,因而相较于NP实现了明显的计算效率提升。但当处理更大的数据集L3时,NP和SC超过3个小时没能返回结果,而AS依然能以较快的效率完成计算。

表5 跨越网格数据处理方法对比实验结果Tab.5 Experiments on cross-grid data processing methods
实验3 树状合并方法对比实验
对顺序合并方法(Sequential Merge,SM)、二叉树合并方法(Binary Tree-like Merge,BTM),以及本文采用的给定深度树状合并方法(Depth-given Tree-like Merge,DTM)3种方法进行对比,结果见表6。显而易见,两种树状合并方法均较顺序合并方法优越。当数据量增加时,加速比更加明显,BTM和DTM相较于SM在L3数据集上分别实现了4.2和5.4的加速比。这是由于数据量的增加,而BTM合并过程中的处理效率却未提升,更加凸显了顺序合并方法的瓶颈。此外,DTM较BTM好,利用较DTM中小的深度h实现了更高的计算效率。这是由于深度增减小后,计算中间结果的等待时间以及网络开销也均减少了,在计算效率和计算资源间达到了较好的平衡。同时,除Funion操作外,3种方法的开销时间基本相等。

表6 树状合并方法对比实验结果Tab.6 Experiments on tree-like merge methods
但是h设置需要综合考虑数据总量以及数据分块数量p。为了验证给定深度树状合并方法中h与数据集以及数据集分块数量p之间的关系,相关实验结果见表7和表8,实验中c=32。表7得出,3个数据集在同等分块(分块足够大)情况下,最优的h均接近log2p-2,即p固定时,对于相同大小的数据集,h的最优深度大致相同。类似的,根据表8,当p变化时,最优h随着p的变化而变化。一步说明本文数据划分方法的效果;实验1的结果已经说明空间填充曲线带来的明显性能提升,这样做方便对其他方法的优化效果进行说明。SPBM优化前的方法为Algorithm3。由于线矢量数据更复杂、具有代表性,且Algorithm1原文中采用线矢量数据测试,因此,本文比较实验均基于线矢量数据进行。
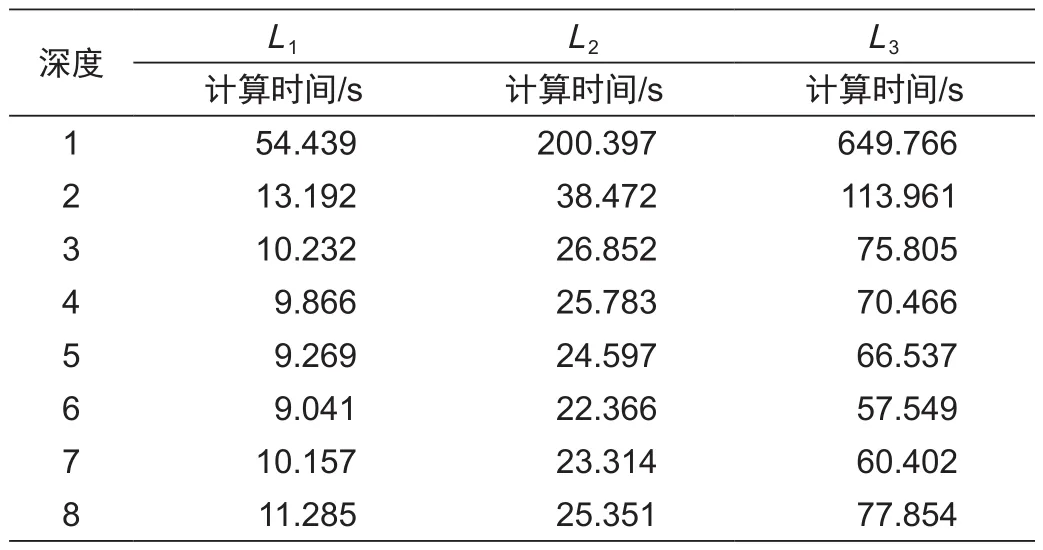
表7 固定p=256,不同数据集时深度参数h影响Tab.7 Fixed p=256, depth h impacted on the experiments on various data
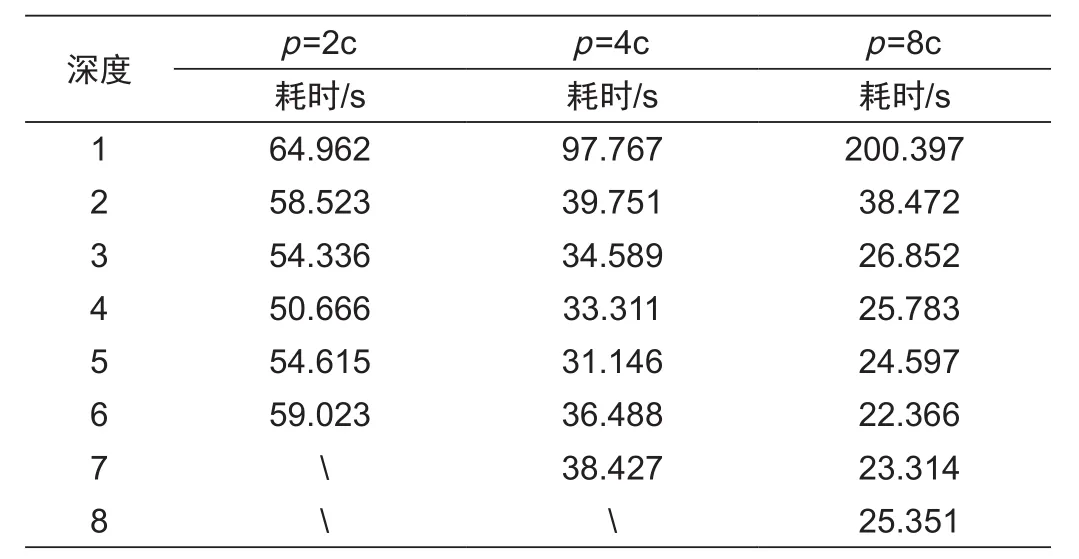
表8 固定数据集L2,不同p时深度参数h影响Tab.8 Fixed data=L2, depth h impacted on the experiments on vary p
在单机环境中,实验结果如图3所示,对于等待3个小时没能返回结果的情况不予列出。SPBM在4个数据集上的计算效率均最高,且优化效果随着数据量增加而更加明显。处理L1时,SPBM与Algorithm1、Algorithm2差异较小。但处理分布不均衡、存在很多单条大数据的L2时,SPBM的优越性立马体现出来。当应对更加密集的L3时,SPBM和Algorithm1较Algorithm2的优势进一步扩大,因为前两种方法采取了二叉树状合并,而后者的顺序合并方法的瓶颈随着数据量增加而愈加凸显。由于没有采取优化措施,Algorithm3的缺点很明显,在4个数据集上的实验处理效率都不高。PostGIS是基于数据库的方法,其中也采取了树状合并方法,性能比较稳定且能够应对较大的数据集,优势随着数据量增加而增加,在L3和L4上的计算效率超过了Algorithm2。实验结果也表明,相较之下QGIS的处理效率仅比Algorithm3稍好。
实验4 算法比较实验
在单机计算环境和集群环境下都进行了比较分析。SPBM是本文提出的方法。Algorithm1基于文献[9-10]中均采取的按节点数量的任务划分和两两树状合并方式这两种优化措施;Algorithm2基于文献[11]中采取的等弧段的任务划分方式。这两种方法只是部分优化措施的使用,和原文有一定区别,既因为实现平台,又因为数据不同且原文献中没有对缓冲区计算距离进行说明。此外,Algorithm1和2均采取了本文提出的空间填充曲线编码的划分方法,有以下两点原因,Algorithm2原文中未在超过1万条的数据集上进行实验,而在本实验中,将要应对20万条以上的数据集,这样改进也能进

图3 单机环境中算法性能比较Fig.3 Algorithm comparison in standalone environment
在集群环境中,与Algorithm1、Algorithm2、Algorithm3以及CitusData进行了比较。实验结果如图4所示,与单机环境中比较类似。其中CitusData采用先在从节点计算,再统一到主节点上合并的方法。由于任务分解以及分布式计算等带来的优化,CitusData在L2和L3上的性能较Algorithm2好;但是应对L4时,由于子任务结果的结构十分复杂,合并时效率受到影响,并未能计算出结果。综合看来,SPBM的效率较其他Algorithm提升了50%以上。

图4 集群环境中算法性能比较Fig.4 Algorithm comparison in cluster environment
4 结束语
在大规模数据缓冲区计算过程中,本文采取一种基于空间填充曲线排列码进行区域划分的缓冲区分析并行算法(SPBM),在Hilbert空间填充曲线排列码的基础上实现了自适应数据划分;对造成数据倾斜的单条大数据进行近似切分处理;此外,以负载均衡为目标进行任务分解;并通过给定深度的“树状”归并方法最大化缓冲区计算效率。通过实验可以证明本方法的科学性和高效性。
空间缓冲区分析涉及大量拓扑关系判断和迭代计算,通过实验比较确定了本文的优化方法的可行性,也为其他空间分析方法提供了一种参考。由于空间缓冲区计算涉及点、线、面等多种数据类型,面数据的结构更为复杂,针对空间面矢量数据的优化方法是下一步的研究方向。

