湖北省开发区开发强度差异特征及效益响应研究
夏令军, 刘艳芳,2,王程程,彭明军
(1.武汉大学 资源与环境科学学院,湖北 武汉 430079;2.武汉大学 教育部地理信息系统重点实验室,湖北 武汉 430079;3.武汉市国土资源和规划局,湖北 武汉 430014)
0 引 言
开发区是各级政府为促进经济发展,在具有开发前景的区域内划出的实行特殊政策的区域,作为推动区域经济发展的增长极,是我国快速工业化和城市化的重要动力和主要载体[1]。相较于城市其他区域,开发区开发建设强度明显更高[2]。但同时,开发区发展过程中又存在开发秩序混乱、土地利用粗放、产业低质同构、开发区重复建设等问题[3-5]。开发区开发强度反映了开发区整体的现状承载水平,不仅包含开发区土地利用强度,也包含建筑活动强度。合理控制开发强度是提高土地利用效率的关键[6]。
目前,学术界关于开发强度的研究主要集中于区域整体开发强度、城市土地开发强度和城市中心区开发强度等方面,如赵亚莉等以建设用地面积占该区域土地总面积的比例为土地开发强度的表征指标,运用GIS和经济计量模型,探讨了1996-2008年长三角地区城市土地开发强度的特征及其影响因素[6];周炳中等从5个方面构建指标体系对长三角地区土地资源开发强度进行了定量评价[7];刘艳军等定量分析了1995-2009年中国区域开发强度与资源环境水平的耦合关系[8];尧德明等运用参照系比较法,对海南省及其18个市县的土地开发强度进行了定量评价[9];赵亚莉运用222个地级及以上城市的面板数据分析了城市土地开发强度差异及影响因素[10];王忠诚等研究了城市中心区的土地开发强度特征[11]。以上研究一般以行政区为研究单元,表征开发强度的指标相对单一。现有的关于开发区开发强度的研究则主要强调开发强度指标的规划控制[12],多以开发区内地块和单个建设项目为研究单元[13],表征的指标一般为容积率、建筑密度和建筑高度等[14-15],对开发区整体开发强度的研究较少。学者们主要从省、市等不同空间尺度[16-17],构建指标体系[18-19],结合相关模型方法[20-22]来进行开发区土地集约利用评价,开发区开发强度的内涵仅被作为评价指标体系中的一部分,由此得出的评价结果难以刻画开发区开发强度与用地效益之间的关系,也难以揭示开发区开发强度与城市发展之间的关系。基于此,本研究以湖北省119个开发区为研究对象,构建二维度的指标体系,采用熵值法、泰尔指数、方差分析和计量模型等方法测度开发区开发强度,分析其差异特征,并探求开发区开发强度的效益响应情况,旨在进一步揭示开发区发展规律。
1 数据与研究方法
1.1 指标选取与数据来源
已有研究中,区域开发强度一般从人口、经济、土地、资源和生态等多维度来刻画[7],而城市土地开发强度一般仅以建设用地比重[10]来表示,城市中心区开发强度则以地块为单元,考虑中心区的建筑密度,容积率和建筑高度[11]等。本文针对湖北省119个开发区,分别从宏观的土地利用强度和微观的建筑活动强度两方面来表征开发区的开发强度。在东部地区产业向中西部转移的背景下[23],中西部地区开发区作为承接产业转移的主阵地,大多数仍以制造业工业为主。所以土地利用强度选取土地建设率和工业用地率两个指标,土地建设率反映了开发区整体的土地开发情况,工业用地率反映了工业活动的开发强度。建筑活动强度则选取工业用地综合容积率和工业用地建筑系数两个指标,从纵向尺度来刻画开发区开发强度。指标体系包括目标层,准则层和指标层3个层次,具体见表1。

表1 开发区开发强度指标体系、信息熵及权重Tab.1 The index system, information entropy and weight of development intensity in development zone
截至2013年,湖北省共有各类型开发区130个(不含湖北神农架盘水生态产业园区),其中国家级开发区12家,省级开发区118家。开发区批准规划面积达5106.9km2,实际占地面积1976.6km2。2013年全省开发区规模以上工业总产值27194.3亿元,占全省规模以上工业总产值的69.36%,税收总额达到1233.26亿元。由于部分开发区统计指标缺失,在充分评估各指标数据的完整性、可操作性以及样本代表性的基础上,本文选取119个开发区为研究对象,占开发区总数的91.5%,其中国家级开发区11家,除神农架林区外,其他市、州均有分布,一定程度上能够反映湖北省整体开发区的发展情况,各开发区空间分布如图1所示。开发区开发强度指标数据来源于湖北省各开发区2014年《开发区土地集约利用评价技术报告》,评价时间节点为2013年12月31日,其他相关社会经济指标数据来源于《2014湖北统计年鉴》及2014年湖北省各市、州统计年鉴。

图1 湖北省开发区空间分布Fig.1 Spatial distribution of development zones in Hubei province
1.2 研究方法
1.2.1 熵值法
熵是对不确定性的一种度量,信息论中用信息熵来度量系统的无序程度,而信息则是有序程度的度量,两者绝对值相等,符号相反[24]。在由多个指标组成的评价体系中,某个指标的指标值离散程度越大,其信息熵就越小,信息量则越大,故该指标的权重值也应该越大;反之也成立[25]。据此,可以根据指标之间数据的离散程度,客观地对各指标的权重进行赋值,避免人为主观因素的影响。
针对本文的评价指标,构建一个由m个开发区,n个指标构成的原始数据矩阵X={xij}m×n(i=1,2,…,m;j=1,2,…,n),xij表示第i个开发区第j个指标的值。运用熵值法计算各指标权重的步骤[26]如下:
1)数据标准化
由于各指标的量纲,数量级和正负效应等存在差异,故需要标准化。这里采用最大最小值标准化方法,对于正向指标:,对于负向指标:。
2)计算标准化矩阵
为了避免对数计算的影响,先将xij进行坐标平移,yij= xij+A,A为平移距离(这里A=0.01)。再根据公式:pij=yij/∑i=1myij),得到标准化矩阵P=(pij)m×n。
3)计算第j项指标的信息熵ej和冗余度djdj衡量了指标间的差异程度,信息熵越小,指标间差异越大,指标就越重要。
4)计算第j项指标的权重

进而可以计算出开发区i的开发强度DIi=。
1.2.2 泰尔指数
泰尔指数是衡量不平等和差异的一个重要指标,由于其具有可加性和可分解性,被广泛应用于区域差异方面的研究[27-28]。泰尔指数可以在自定义分组的基础上,将区域整体差异分解为组间差异和组内差异,能够分别度量组间差异和组内差异对总体差异的贡献率。本文用泰尔指数来表征湖北省开发区开发强度的区域差异,其计算公式[21]为:

式中,T表示泰尔指数;Tb表示开发区开发强度组间差异;Tw表示开发区开发强度组内差异;I是将开发区按某种特征分类得到的组数;J指大组内开发区的个数;Yi/Y表示第i组开发区开发强度占所有开发区开发强度的比重;Ni/N表示第i组开发区总面积与所有开发区总面积的比重;Yij/Yi表示i组中第j个开发区开发强度占该组总开发强度的比重;Nij/Ni表示i组中第j个开发区面积占该组开发区总面积的比重。
2 开发区开发强度差异分析
2.1 开发区开发强度总体特征
根据熵值法确定各指标权重后见表1,得到湖北省119个开发区的开发强度。不同开发区之间开发强度差异明显,其中湖北公安经济开发区最高,达0.7831,最低的是湖北利川经济开发区,仅为0.2109,前者大约是后者的3.7倍。湖北省开发区整体平均开发强度为0.4937,高于平均水平的占52.1%。
将湖北省划分为江汉平原、鄂东南、鄂东北、鄂西南、鄂西北五大区域 。表2显示,江汉平原地区开发区个数最多,平均开发强度最大,这一区域人口密集,物产丰富,一直以来是湖北省重点发展区域。此外鄂东南和鄂西北地区的平均开发强度也相对较高,均在0.5以上,而鄂西南和鄂东北地区的平均开发强度较低。从各开发区开发强度的空间格局(如图2所示)可以看出,虽然各地区均有不同层次开发强度的开发区分布,但开发强度高的开发区主要集中在江汉平原的荆门、荆州、武汉和仙桃市,鄂西北的十堰和襄阳市,鄂东南的咸宁市等;而鄂西南的恩施州,鄂东北的黄冈市,以及江汉平原的天门、潜江和鄂州等地区开发区开发强度较低。

表2 湖北省不同区域开发区个数及开发强度Tab.2 The numbers and development intensity of diあerent regional development zones in Hubei province

图2 湖北省开发区开发强度空间格局Fig.2 Spatial pattern of development intensity in development zones of Hubei province
2.2 开发区开发强度区际与区内差异
以不同区域为分组标准,根据公式(1)得到湖北省开发区开发强度的泰尔指数,并进一步分解为区域间差异和区域内差异,计算各区域对总体差异的贡献率见表3。湖北省开发区开发强度的泰尔指数为0.5368,说明整体开发区开发强度差异明显。
从贡献率的分解结果来看,五大区域间开发强度差异为0.0135,对总体差异的贡献率仅为2.51%,而五大区域内部开发强度差异为0.5233,对总体差异的贡献率为97.49%。区域内部差异贡献率远远大于区域之间的差异贡献率,说明开发区开发强度差异主要来源于区域内部。就五大地区内部对总体差异的贡献率来看,江汉平原地区贡献率最大,达到43.37%,其次是鄂西北地区为22.86%,鄂东南地区为13.56%。鄂东北和鄂西南地区贡献率都在10%以下,说明其内部开发区开发强度差异相对较小,各开发区建设发展水平相近。

表3 湖北省开发区开发强度泰尔指数及不同区域贡献率分解Tab.3 Tail index and the contribution rate decomposition of diあerent regions in the development zones of Hubei province
2.3 开发区开发强度市际与市内差异
以市级行政区为分组依据,除了神农架林区,共分为16组,分别计算各市州之间和市域内部的泰尔指数差异贡献率。各市州之间开发区开发强度差异对总体差异的贡献率为8.65%,市域内部的差异贡献率为91.35%,可见市域内部的开发区开发强度差异同样远远大于市域之间的差异。图3a表明,不同城市内部开发区开发强度差异有所不同,其中,武汉市、荆州市和十堰市贡献率均超过了10%,其内部开发区开发强度差异明显,三者差异占总体差异的46.76%,接近一半。天门市贡献率为0,是因为天门市只有一个开发区,不存在内部差异。鄂州市和仙桃市的贡献率均不足1%,潜江市和孝感市不足2%,说明这些城市内部的开发区开发强度相差不大,基本处于同一发展水平。
从不同城市内部差异贡献率的空间分布(图3b)可以进一步细致地揭示区域开发强度差异,也能清楚地看到其存在尺度嵌套现象。江汉平原地区的城市内部差异贡献率有4种类型,鄂东南地区有3种类型,鄂西北地区有2种类型,而鄂东北地区的城市处于同一类型,类型越多,表明地区内差异越大,这与前面按区域分组的各地区差异贡献率情况基本相同。

图3 不同城市内部开发区开发强度差异对总体差异的贡献率(a)及空间分异(b)Fig.3 Contribution rate to the overall diあerence (Fig.a) and spatial diあerentiation (Fig.b) of the development intensity diあerence of development zones in diあerent cities
2.4 不同类型、等级与成立年限开发区开发强度差异
开发区开发强度差异除了空间上的组间差异和组内差异外,开发区类型、等级和成立年限等自身属性的不同分类之间也可能存在差异。湖北省开发区类型根据《开发区土地集约利用评价规程》(2014年度试行)分为工业主导型和产城融合型;开发区等级根据批复设立机构分为国家级开发区和省级开发区;2006年国家发改委颁布《中国开发区审核公告目录》(2006版),湖北省很多开发区在2006年才正式成立,故以2006年为节点,将2006年以前成立的开发区认为是成立年限长的类型,2006年及以后成立的开发区属于成立年限短的类型。各类型开发区情况见表4。
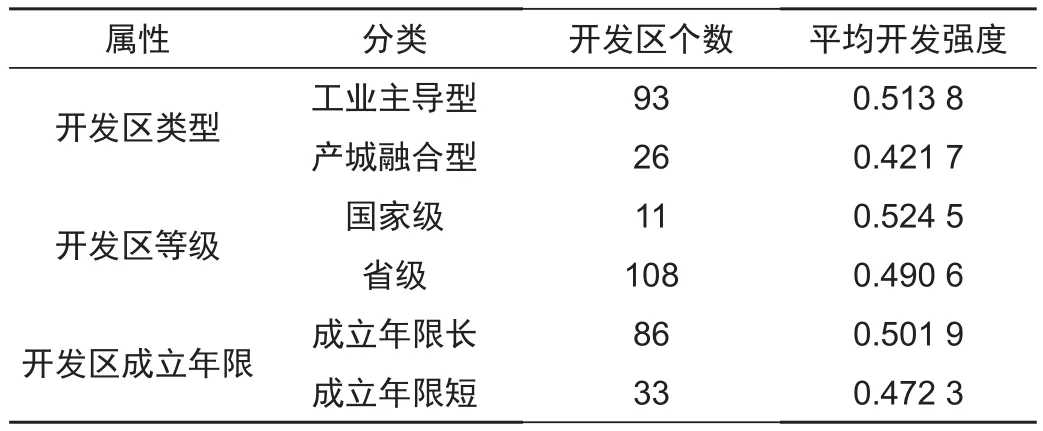
表4 开发区属性分类Tab.4 Attribute classification of development zones
为了考察不同类型、不同等级和不同成立年限开发区之间开发强度是否存在显著的差异,这里选用方差分析的方法来检验这种差异是否存在。方差分析是一种参数检验方法,能够检验观测变量在控制变量的不同水平上是否存在显著差异。这里的观测变量即是各开发区的开发强度,控制变量为开发区类型(Type)、等级(Level)和成立年限(Age),每个控制变量有两种水平。以下检验过程均在SPSS22.0软件的相应模块中完成,通过单样本K-S检验和方差同质性检验显示,样本数据属于正态分布且方差齐性,满足方差分析条件,由于控制变量不只一个,故采用多因素方差分析,检验结果见表5。

表5 开发区开发强度多因素方差分析结果Tab.5 The results of multivariate analysis of variance of development intensity of development zones
结合表4,从表5可以看出,开发区类型在1%的水平下通过了显著性检验,表明工业主导型和产城融合型开发区其开发强度存在显著差异,这是由于开发区发展定位不同,产城融合型开发区更多地处于转型升级阶段,产业发展由传统的加工制造向现代化工业和服务业转变,更多注重产业升级与城市综合服务功能的提升,工业用地率较低,故其平均开发强度相对工业主导型开发区来说比较低。开发区成立年限在5%的水平下通过了显著性检验,即开发区成立年限也影响开发区的开发强度,虽然从平均开发强度来看,成立年限长的开发区(0.5019)与成立年限短的开发区(0.4723)相差不大,但成立较早的开发区,一般是城市重点发展的产业集聚的增长极,工业活动规模相对较大,基础设施相对完善,平均开发强度也相对较大。开发区等级没有通过显著性检验,说明国家级和省级开发区开发强度不存在显著差异,这可能是由于国家级开发区个数相对较少,且国家级开发区产业层次相对较高,开发区转型升级处于领先阶段,传统以高密度开发的工业发展模式逐渐转变,虽然有更多的优惠政策和吸引力,但相较众多以工业为主的省级开发区而言,其开发强度并不明显偏高。
3 开发区开发强度效益响应
开发区作为推动区域经济发展的重要载体,其发展效益是评价开发区成功与否的关键。开发区开发强度与开发区效益关系如何?本文主要从开发区自身效益和开发区对城市的综合效益两方面来考察。开发区工业活动的效益可以从上缴的税收来反映,所以用工业用地地均税收来表示开发区自身效益(ZB);开发区对城市的综合效益按以下公式得出:

式中,CBi表示第i个开发区对城市的综合效益;gi表示第i个开发区的规模以上工业增加值;Gi指第i个开发区所在地级市的规模以上工业增加值;li表示第i个开发区已建成城镇建设用地面积;Li指第i个开发区所在地级市城镇建设用地面积。
设定效益响应模型为:

式中,Bi依次取开发区自身效益ZBi和对城市的综合效益CBi;DIi为第i个开发区开发强度;α0,α1为回归系数,εi为随机扰动项。
运用SPSS22.0软件进行估计,结果见表6。

表6 效益响应模型估计结果Tab.6 Estimation results of benefit response model
湖北省开发区开发强度对自身效益(α1=0.855)和对城市的综合效益(α1=1.087)均有一定的正面促进作用,这是因为对处于中部地区的开发区来说,工业规模的扩大有赖于土地高强度的开发。从可决系数R2来看,开发强度仅能解释自身效益的4.8%,解释对城市综合效益的5.6%,说明开发强度并不是提高开发区效益的主导因素,如开发区产业结构、环境保障条件、配套政策支持、企业创新和集聚、管理绩效等都能影响开发区效益。这也从另一个角度揭示了开发区需要走土地集约利用之路,转变发展方式,积极寻求转型升级,仅依靠高强度的开发并不能有效提高开发区效益。
4 结束语
本文以湖北省119个开发区为研究对象,采用熵值法、泰尔指数、方差分析和计量经济模型等方法系统分析了湖北省开发区开发强度的差异特征及其效益响应,研究表明:
1)湖北省不同开发区开发强度差异明显。江汉平原、鄂西北和鄂东南地区的开发区开发强度相对较高,鄂西南和鄂东北地区开发强度相对较低。区域内的差异远远超过区域间的差异,区域内的差异贡献率达97.49%,其中江汉平原的贡献率最大,为43.37%;市域内的差异也远远大于市域间的差异,市域内的差异贡献率亦超过90%,湖北省开发区开发强度个体异质性明显。不同类型和不同成立年限的开发区开发强度存在显著的差异,但不同等级的开发区之间开发强度差异不明显。
2)湖北省开发区开发强度的效益响应不明显。整体上开发区开发强度对开发区自身效益和对城市的综合效益均有一定的正面促进作用,但并不是影响开发区效益的主导因素。这也从另一个角度揭示了开发区仅依靠高密度的开发并不能显著提高开发区效益,需要转变低效发展方式,提高开发区土地集约利用水平。
尽管本研究取得了一些成果,但仍有进一步完善的地方。限于数据原因,本文采用的是截面数据,仅揭示了湖北省开发区开发强度某一时刻的静态差异特征,无法描述开发强度的动态变化,后续可以采用面板数据来进行动态分析。

