顾及地形的滇中引水工程最低成本线路研究

鲍 倩，葛 莹，闻 平，童麟凯，司建强

(1.河海大学 地球科学与工程学院，江苏 南京 211100；2.中国电力建设集团 昆明勘测设计研究院有限公司，云南 昆明 650051)

0 引 言

云南省滇中高原地区是云贵高原重要的组成部分，所占面积大约9.63×104km2。它具有特殊的地理位置、复杂的地形状况，主要表现为山岭纵横，地势波状起伏，海拔高差悬殊，是长江流域三大干旱区之一。同时，滇中高原地区又是云南省社会经济发展的核心。正因为如此，中国工程院2000年编写的《21世纪中国可持续发展水资源战略研究》报告明确指出：经济较发达的滇中高原地区，因地势高、水利骨干工程缺乏，倘若建设滇中高原地区补水工程，就能满足该地区大开发需要。因此，滇中引水工程项目受到广泛重视[1-6]。

引水工程线路规划是这类项目建设前期的主要内容，它除了要分析当地水文条件之外，还要考虑地形、工程地质、交通等因素的影响[7-9]。杜伟超[10]认为地形对引水工程线路规划有影响；郭永鑫[11]认为引水工程线路规划要充分利用地形的自然高差, 当地形条件许可时优先考虑自流输水。但上述文献对于如何在引水工程线路规划时引入地形因素并没有详细说明。一般来说，坡度是衡量工程建设成本的重要因素[12]；而地势起伏度是描述地貌形态的定量化指标，它可以在宏观上较好地反映地面起伏特征[13]。所以，本文考虑的地形因素主要是指地势起伏度和坡度。

本文从地形的角度出发，以滇中地区引水工程线路为研究对象，在广泛收集引水工程线路规划资料的基础上，分析滇中地区地形特征，引入地势起伏度和坡度作为度量地形的参数。并运用数理统计学的均值变点分析法，探讨地势起伏度最佳统计单元的确定，以期较准确地反映滇中地区复杂地形特征，解决地势起伏度最佳统计单元确定的随意性。在此基础上，运用GIS技术生成研究区地势起伏度和坡度数据，运用专家打分评价方法，建立关于引水工程线路规划的地势起伏度、坡度评价标准，再结合基于栅格的成本加权分析法，构建出滇中引水工程地形成本栅格。以适用于栅格数据的Dijkstra算法为理论基础，编写Python语言程序，求解出基于成本栅格计算的引水工程最低成本线路。

1 地势起伏度的提取

地势起伏度是区域海拔高度和地表切割程度的综合表征[14]。它是指一定统计单元内最高点和最低点高程之差[15-16]，其公式为：

式中，Rs表示s×s统计单元内的地势起伏度，Hmax表示该统计单元内最大高程值，Hmin表示该统计单元内最小高程值。最佳统计单元的确定能恰到好处地反映山体的完整性，所以计算地势起伏度的关键是确定最佳统计单元[17]。利用DEM数据提取地势起伏度是获取地表信息的有效手段[18-19]。本文以ZY-3DSM为地形数据源，在ArcGIS软件支持下，借助Python语言，结合GIS窗口分析方法，编程实现统计单元3×3，4×4，5×5，…60×60地势起伏度计算。

为了描述不同统计单元下的地势起伏度，本文以栅格整体地势起伏度的均值为全局指标，对统计单元与地势起伏度均值进行多项式方程拟合，如图1所示。拟合曲线的判定系数为R2=0.997 4，经拟合优度检验，曲线拟合效果良好。从理论上来说，随着统计单元的增加，地势起伏度均值逐渐增大后趋向平缓，而由陡变缓所对应的点即是最佳统计单元[17]。尽管如此仅从图1中很难获得地势起伏度的最佳统计单元。

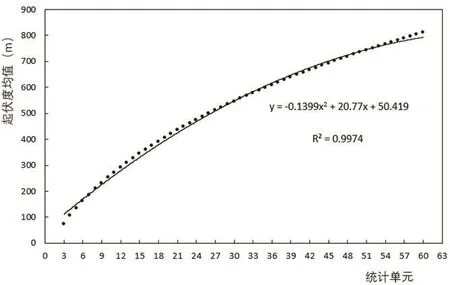
图1 统计单元与地势起伏度均值的拟合曲线Fig.1 Fitting curve of statistical unit and mean of relief

之前研究多为人工判断曲线上由陡变缓点的位置，这种定性方法存在随意性[20-21]。为了能定量搜索地势起伏度最佳统计单元，本文采用均值变点分析法确定研究区地势起伏度最佳统计单元。均值变点分析法是一种对非线性数据进行处理的数理统计方法，它对恰有一个变点的检验非常有效[22]。本文所指的变点是“地势起伏度均值突然发生变化的点”,这种突然发生变化的点能反映地势起伏度某种结构的变化。

本文以滇中引水工程线路为例，ZY-3 DSM为数据源、GIS窗口递增原理获得的地势起伏度均值为样本，通过均值变点分析法寻找地势起伏度均值变化的点，以确定最佳统计单元。均值变点分析法原理如下：

1）设样本{xi,i=1,2,…,N},将其分为x1,x2,…,xi-1和xi,xi+1,…,xN两段,计算每段样本的算术平均值和，以及两段样本方差之和Si

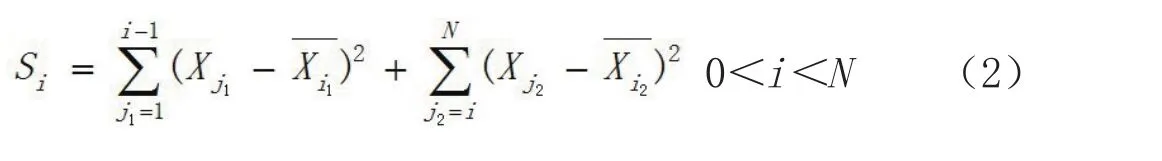
2）计算样本的总体算术平均值X和总体方差S

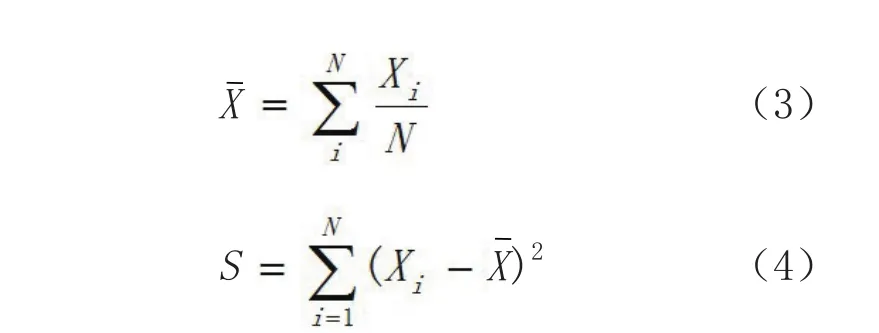
3）变点的存在会使S和Si的差值增大，两者差值最大对应的点即为变点，故计算S和Si的差，其差值最大对应的i即为变点

式中，S表示总体方差，Si表示两段样本方差之和，Di表示S与Si差值，Di最大值即为变点。

本文在ArcGIS云平台上，利用Python语言编程实现地势起伏度最佳统计单元的确定，其算法步骤是：①以上述地势起伏度的均值为样本，令i=1,2,…, N-1，并运用式（2）计算两段地势起伏度均值方差之和Si；②运用式（3）和式（4）计算地势起伏度均值X（X={xi，i=1,2,3…,N}）的总体算术平均值X和总体方差S；③运用式（5）计算S和Si的差值Di，并取Di的最大值对应的点i，这一点正是i的变点。表1为均值变点分析法的计算结果。

表1 均值变点分析法的计算结果Tab.1 Statistical results of mean change points analysis

表1显示随着统计单元的增加，Di值逐渐增大；当它增大到一定程度时，即统计单元为24×24，Di值达到最大，此时统计面积为24 km2。此后，Di值又逐渐减小。依均值变点分析法可知，Di最大值对应的点i即为变点，故研究区最佳统计单元为24×24。该值与涂汉明等[17]得出的适合我国的最佳统计面积是21 km2非常接近，所以，在这一统计单元下生成的地势起伏度能很好地反映滇中地区的地形基本特征。

2 引水工程最低成本线路建模

2.1 引水工程最低成本线路总体框架

引水工程最低成本线路求解是建立在地形评价的基础上，其建模方法如下：①在ArcGIS环境下，按掩膜提取研究区DEM数据，再由DEM数据派生坡度图；②使用程序生成各统计单元的地势起伏度，由此确定地势起伏度的最佳统计单元，生成最佳统计单元的地势起伏度图；③运用专家打分评价方法，建立滇中引水工程地形评价体系，以确定坡度、地势起伏度的权重，并给出合理的等级划分标准；④利用GIS技术对坡度、地势起伏度进行等级换算、按权重叠加运算等操作，构建出滇中引水工程地形成本栅格；⑤按照栅格数据的Dijkstra算法[23]，求解出引水工程的最低成本线路。引水工程最低成本线路算法如图2所示。

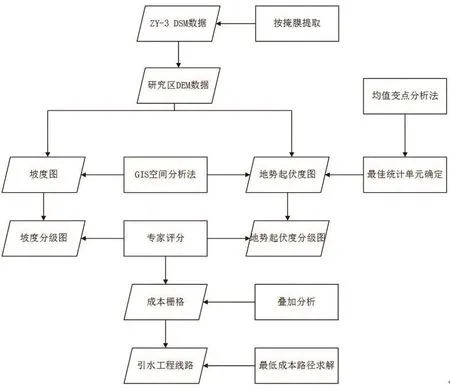
图2 顾及地形的引水工程最低成本线路的算法流程Fig.2 The technical flow of the minimum cost line of water diversion project

2.2 引水工程最低成本线路求解

引水工程线路最低成本线路求解依据GIS栅格数据最短路径分析。最短路径分析是基于成本栅格寻找指定的源点和目标点之间符合某种度量的最“短”路径，Dijkstra算法是广泛应用于网络数据的最短成本路径算法。但由于数据组织方式差异，本文采用的栅格数据Dijkstra算法与网络数据有所不同[24-28]。

在求解引水工程最低成本线路之前，首先要构建地形成本栅格。在分析地形对滇中引水工程线路影响的前提下，根据引水工程项目的评价目标，运用专家打分评价法作为引水工程项目规划的评价方法。具体地说，第一步考虑地势起伏度、坡度为最低成本线路的影响因子，第二步通过专家法[13]结合滇中高原地形特点，建立1至9标度的等级序列，见表2，第三步确定坡度、地势起伏度的指标影响权重分别是0.3和0.7，第四步利用GIS技术采用栅格的成本加权分析法，计算地形要素和地形指标的组合权重，构建滇中引水工程项目的地形成本栅格。

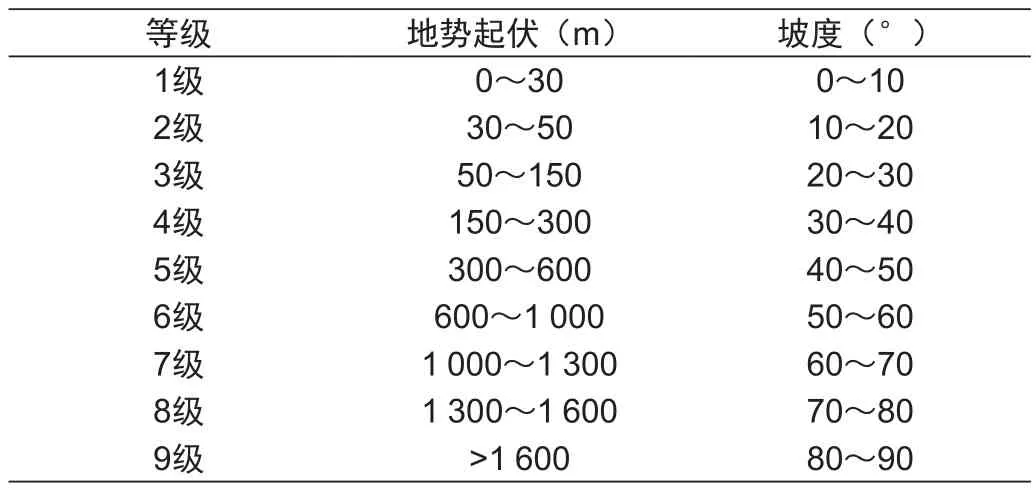
表2 滇中引水工程的地形影响因子等级划分Tab.2 Classification of terrain influence factor in Dianzhong water diversion project

在上述构建成本栅格的基础上，结合指定的源点和目标点坐标，以适用于栅格Dijkstra算法为理论基础，使用自编Python程序，计算出每个栅格单元到源点的最小累积成本，标记出每个栅格最低成本线路的走向，在ArcGIS环境下求解出源点到目标点的最低成本线路。滇中引水工程最低成本线路如图3所示。

图3 顾及地形的引水工程最低成本线路图Fig.3 Water diversion project route based on regional terrain

3 结束语

滇中地区是长江流域三大干旱区之一，资源性缺水与工程性缺水已成为制约滇中地区乃至云南省经济社会可持续发展的瓶颈，建设滇中高原地区引水工程，可满足该地区大开发需要。然而，该地区地形地貌复杂，施工难度大，引水工程线路布置很困难，故引水工程线路规划的重要性列于首位。针对该问题，本文分析了滇中地区地形状况，引入地势起伏度和坡度作为度量地形的参数。为了较准确地反映滇中地区复杂地形特征，解决地势起伏度最佳统计单元确定的随意性，本文通过自编Python程序实现其最佳统计单元的确定，生成地势起伏度和坡度图。并运用专家打分评价方法，建立滇中引水工程地形评价体系，以确定坡度、地势起伏度的权重，并给出合理的等级划分标准。采用基于栅格的成本加权分析法，构建滇中引水工程地形成本栅格。并基于构建的成本栅格，将引水工程线路规划问题转化为GIS最低成本路径的求解问题，以栅格数据Dijkstra算法为基础，编写Python语言程序，求解并输出引水工程最低成本线路。本文从地形角度出发，研究了滇中引水工程线路智能布置的方法，对于顾及地形的滇中引水工程线路规划做了有益尝试。