基于多密度聚类算法的路网提取

朱鸿博，王山东，李 贺，方 琪，征 程

(河海大学 地球科学与工程学院，江苏 南京 210000)

0 引 言

随着国家经济迅速发展，城市汽车总量持续增长，道路交通拥挤成为制约城市发展的一个瓶颈。如何快速高效实时反映路况成为新的研究课题，而对于路网提取与更新是实现实时反映路况的前提条件。如果导航地图无法做到及时快速更新，其现势性将不能满足应用需求。浮动车轨迹数据凭借其成本低、实时性强、信息量大等优点，逐渐地得到重视，对有效地提取路网提供了强有力的保证。

基于GPS轨迹数据提取路网已经涌现出三类方法[1]：

1）利用各种聚类算法对栅格或是矢量数据聚类；

2）核密度估计算法;

3）轨迹合成算法。

本文主要针对第一种方法研究了国内外的现状。Edelkamp等人[2]最先提出了基于K-Means算法的路网提取方法，并引入了拟合方法来表示道路中心线，进一步提高了路网的精度。Worrall等人[3]在K-Means算法基础上，提出用简洁的线段与弧模型来表示生成的路网。Schroedl等[4-5]提出一种类似K-means 算法的路网提取方法，并引用最小二乘法拟合道路中心线，但是K-means算法不能满足自动确定类簇数目的要求，且迭代的过程具有很高的时间复杂度；朱云龙等人[6]将基于网格相对密度的多密度聚类算法用于道路提取，虽然该法能够有效地确定交叉口的位置及数量，能够实现路网结构的快速构造，但是没有考虑不同邻接网格对当前网格影响的不同。基于DBSCAN算法的聚类方法不能很好地确定合适的密度阈值，可能会将相邻的道路特征点合并或者同一个道路特征点拆分。

本文在研究了国内外现状的基础上，提出将基于网格密度因子的多密度聚类算法引入路网提取，该聚类算法通过密度可达性来确定聚类类簇，有效地解决了K-Means算法需要事先设置类簇个数的缺点。且该算法考虑了相邻网格之间的联系，解决了大部分网格聚类算法只考虑网格内包含的浮动车数据，而忽视相邻网格之间数据的相关性的问题。解决了这些问题之后得到的聚类点精度和准确性都有了一定的提高。

1 理论与方法

1.1 疑似特征点提取

浮动车轨迹中道路特征点可以看做是道路发生明显变化的点，即行驶过程中航向角变化较大的点，这些点大都集中在道路交叉口附近。区别于路口转弯点，利用道路特征点来生成路网拥有更好的拟合性，同时也能通过交叉判别，提取出路口转弯点，建立完整的路网。

根据浮动车轨迹中相隔一个频率的前后相邻的两个轨迹点的方向角变化值进行判别，如果变化角度超过一定的阈值，那么就怀疑这两个点在真实转弯点附近，为道路特征点。如图1所示。

图1 路口轨迹点Fig.1 Track point in intersection

以道路交叉口为例，图1中点2和点3应为道路特征点，但是其聚集性不好，并没有聚集到交叉口中心位置，这是由于GPS点的粗粒度特性[7]。根据这样的道路特征点提取路口点不够精确，所以，本文引入聚集性更强的疑似道路特征点。

道路交叉口存在于道路转弯点的行驶方向，因此，我们将转弯点前后两点的行驶方向的交会点作为真实道路的转弯点，并使得行驶方向上当前点与前一点连线的方向角之差小于转向阈值，如图2中，点5为更具集聚性的交叉路口点，即疑似道路特征点。

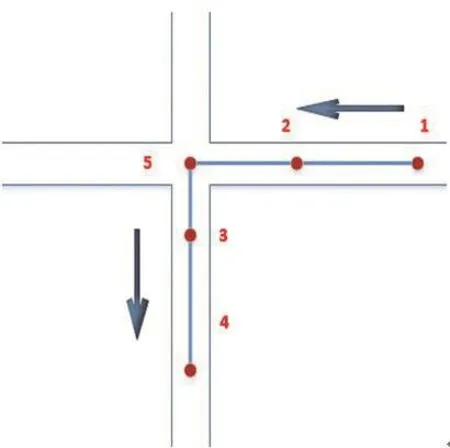
图2 疑似道路特征点Fig.2 Suspected road feature points

疑似道路特征点提取流程图如图3所示。

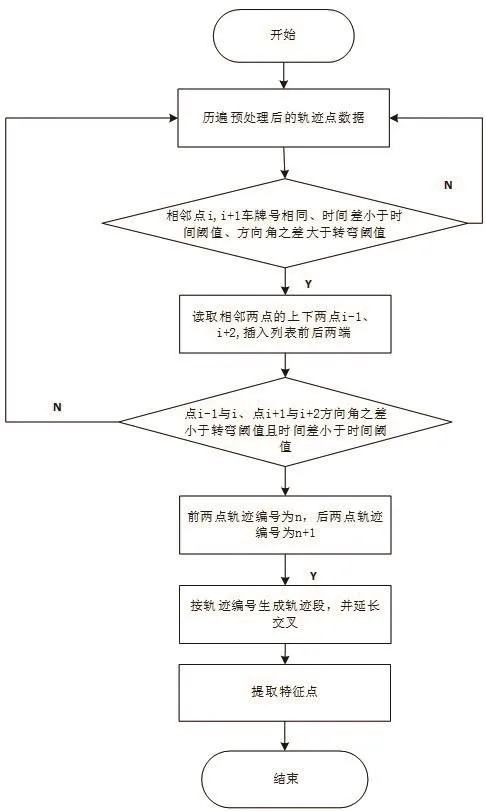
图3 提取流程图Fig.3 Extract flow chart

1.2 基于网格密度影响因子的多密度聚类算法

定义如下：

定义1，数据集X。X={xi,i=1,2,…,n},X是一个二维空间的点集，xi=(xi1, xi2)，代表第i个数据对象，xi1和xi2这里用来描述浮动车轨迹的经纬度坐标。

定义2，网格单元。在研究区域内，设置取值范围，并对该范围进行划分，得到m×n个矩形单元集合U，U={u1,u2,…,um×n}，其中ui为网格单元。

定义3，网格密度。网格单元ui中，数据对象的数目之和称为网格密度，记做den(ui)。当den(ui)=0时，称ui为空单元；当den(ui)＞0时，称ui为非空单元。

定义4，邻接网格。当且仅当网格单元ui和uj有公共边或公共点时，称ui和uj是邻接网格。ui所有的非空邻接网格的集合记为Ngs(ui)。

二维空间中的邻接网格只有两种情况：第一种是有且只有一个公共点，这类我们称为第一类邻接网格；第二类是具有一个公共边，这类我们称为第二类邻接网格。

对于网格ui的非空邻接单元Ngs(ui)，若uj属于上面所说的第α类(α=1，2)，则uj对ui的影响权重ωij为：

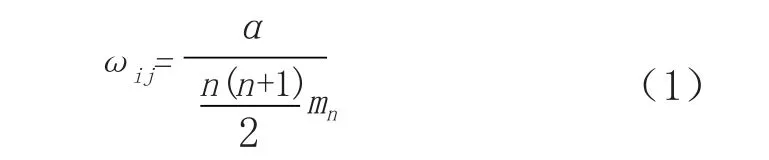
式中，n为空间的维数，mα为Ngs(ui)中属于第α类的非空邻接单元的总个数，

定义5，网格的密度影响因子(impact factor of grid density ,IFGD)。网格ui的IFGD是指ui的网格密度与其非空邻接网格Ngs(ui)中所有网格的密度值与权重值乘积的总和的比值[8]。

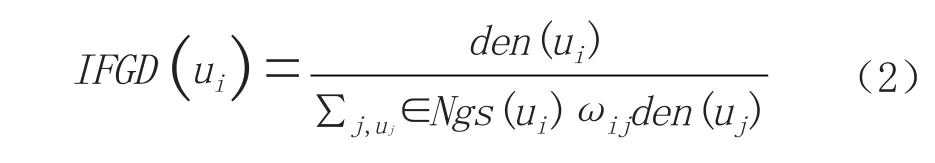
当IFGD(ui)＜1时，说明网格ui的密度值小于邻接网格的平均密度；当IFGD(ui)=1时,说明网格ui的密度值和邻接网格的平均密度相近；当IFGD(ui)＞1时，说明网格ui的密度值大于邻接网格的平均密度。IFGD(ui)的值越大，表明ui处于类簇的中心位置的概率越大，反之，则偏离类簇中心位置的概率越大。

定义6，核心网格。当IFGD(ui)≥1时，说明网格ui更靠近某个类簇的中心，则认为是核心网格。

定义7，直接密度可达。若uj∈Ngs(ui),且满足：

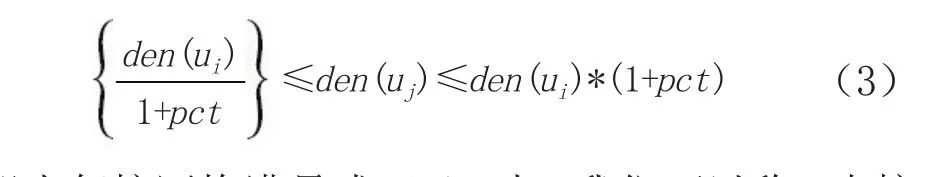
即当邻接网格满足式（3）时，我们可以称uj直接密度可达ui，式（3）中pct是密度浮动参数，易证直接密度可达是对称的，即如果uj直接密度可达ui，则ui也直接密度可达uj。这样就可以在聚类过程中来判别网格是否应当合并扩展成类簇的主要轮廓。

定义8，密度可达。在网格序列u1,u2,…,un中，ui=p,un=q，满足ui直接密度可达ui+1，1≤i＜n，则称网格p密度可达网格q，同样易证网格密度可达是对称的。

定义9，基类。基类C即一个簇的骨架，是一个非空子集，满足：至少存在一个核心网格u0∈C,且任意ui是从u0基于密度可达的，则ui∈C（极大性和连通性）。

基于以上定义，基于网格密度影响因子的多密度聚类算法步骤如下：

1）将数据集D所在的空间范围划分为 m×n个网格单元；

2）计算每个网格单元的密度值和网格密度影响因子；

3）根据定义6提取核心网格；

4）根据密度可达性进行标记、归类，得到类簇。

1.3 基于加权质心的特征点确定

确定了道路特征点的类簇之后，再提取出每个类簇的质心，确定道路特征点的位置，就可以完成道路特征点的最终提取。针对本文这种具有明显集聚性的数据，此处采用了加权求质心的方法[9]。

我们假设一个聚类好的点集数据W={W1,W2,…,Wn}，n为类簇的个数，Wp={wp1,wp2,…,wpm}，为第p个类簇的点集，p=1,2,…,n，m为该类簇内点的个数，wpq={xi,yi},为p类中的一个点，q=1,2,…,m，i=1,2,…,m。每个类簇的质心都是未知的，其坐标为(Xe,Ye)，则加权质心计算公式如下：

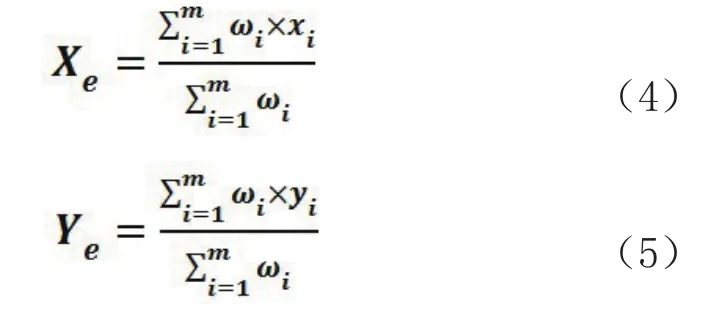
式（4）和（5）中：ωi表示每个疑似道路特征点赋的权重值。这里，根据统计，我们将每个点在其位置出现的次数作为权重值，出现的次数越多，代表其越靠近真实位置，其影响也越大。

通过加权求质心的方法，可以求得每个类簇质心的坐标值，即道路特征点的位置。

1.4 道路拓扑结构及路网构建

基于道路网络几何模型可以得到道路网络拓扑结构，将路网数据中的交叉口和路段以节点-弧段模型的方式记录，即以图的形式存储起来[10]。

本文选取了邻接表表示法，通过创建路段表来存储相关数据和拓扑信息[11]。表结构见表1。

表1 路段存储结构表Tab.1 Section of the storage structure table

表1中路段ID是路段的唯一标识号；道路特征点编号为路段从起始点编号依次记录到路段终止点编号。

有了道路特征点，通过轨迹段的获取，就可以判断相邻道路特征点间是否存在道路段，完成路网的构建。通过判断两个道路特征点之间是否存在一定数量的公共轨迹段，如果存在，则说明这两个点之间可能存在路段，反之，则不一定存在路段。

这里，我们将浮动车的轨迹按照车牌号、采集时间的顺序排列，当满足一定的时间连续性和方向角变化时，可按照同一辆车时间的先后顺序将其转化为车辆的轨迹段T，T={x1,x2,…,xn}，xi为浮动车轨迹点。

对提取得到的道路特征点进行缓冲区生成，将车辆轨迹段所经过的道路特征点按照时间先后顺序排成一个序列R={r1,r2,…,rn}, ri为道路特征点，i=1,2,…,n，则称道路特征点ri和ri+1存在一条公共轨迹段。遍历所有的轨迹段和道路特征点，得到所有道路特征点两两之间公共轨迹段的数量，当数量达到一定的阈值时，则认为这两个道路特征点之间存在直接相连的道路。确定所有道路特征点的邻接关系，将存在路段的道路特征点相连接得到道路段，就完成了路网的构建工作。本文提取路网流程图如图4所示。

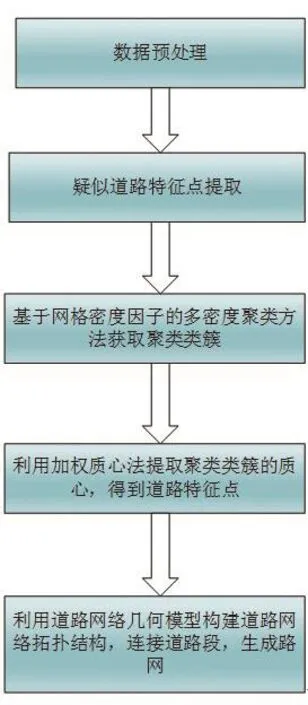
图4 路网提取流程图Fig.4 Flowchart of road network extraction

2 实验结果与分析

2.1 疑似特征点提取

1）实验数据

本文数据是2010年9月南京市区及周边地区的1万多辆出租车1天的轨迹数据，采样频率在30～60 s之间。预处理后的部分轨迹点数据如图5所示。

图5 预处理后部分轨迹点Fig.5 Partial trajectory after pretreatment

2）疑似特征点提取

将完成数据预处理后的轨迹点按照车牌号和采集时间进行排序，得到数据集X={x1,x2…,xn1}，n1为车辆的数量，xi为第i辆车按照采集时间排序的车辆轨迹，i=1,2,…,n1，xi={p1,p2,…,pn2}，n2为第i辆车轨迹点的数量，pj为第i辆车的轨迹点，j=1,2,…,n2，pj={xj,yj,tj,dirj,vj}，其中，xj为pj的经度坐标，yj为pj的纬度坐标，tj为pj的采集时间，dirj为pj的方向角，vj为pj的瞬时速度。设定时间阈值为Δt阈，方向角阈值为Δdir阈，当Δt=ti+1-ti＜Δt阈，且Δdir=diri+1-diri＞Δdir阈时，则认为pi和pi+1为转弯点，将pi和pi-1的连线作为当前路段的行驶方向，将pi+1和pi+2的连线作为即将转入的路段的行驶方向，那么可以认为两个行驶方向的交会点为疑似道路特征点。同时，通过方向角确定出当前车辆的行驶方向。这里根据采样间隔和经验值，设置Δt阈=60 s，Δdir阈=30°，提取出来的疑似道路特征点如图6所示。

图6 疑似道路特征点Fig.6 Suspected road feature points

2.2 基于聚类方法及加权质心提取特征点

1）将实验区域划分成n×m个矩形网格，并统计每个网格内疑似道路特征点的数目，利用基于网格密度影响因子的多密度聚类算法对疑似道路特征点进行聚类。

网格大小的设定对于算法的效果有很大的影响，网格设置太小，会影响算法的效率，网格设置太大，则分类效果不好。这里考虑到正常的道路宽度，并结合经验值和多次实验，将实验区域划分成10 m×10 m的网格，第一类邻接网格有4个，影响因子为1/12，第二类邻接网格有4个，影响因子为1/6。将空网格剔除，设定pct=0.8，通过基于网格密度影像因子的方法进行聚类，剔除噪声点。

2）提取出每个类簇的质心，即道路特征点，结果如图7所示，共265个道路特征点，这些特征点中还包括了道路段上可以进行转向掉头的岔口。将道路特征点和影像图进行比对，发现具有较高的吻合性。

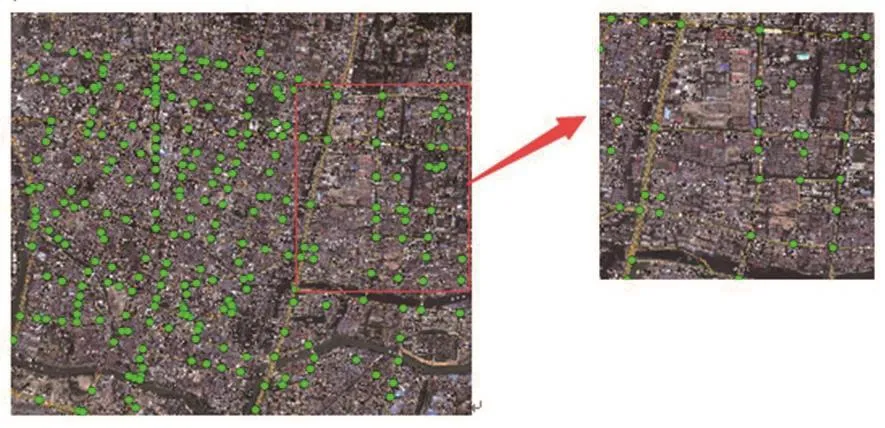
图7 道路特征点Fig.7 Road feature points

2.3 路网生成

将上述步骤生成的道路特征点加入到道路网络模型中构建道路网络拓扑结构，以节点-弧段的方式存储生成轨迹段，通过生成的轨迹段来确定道路特征点的邻接关系，完成路网的提取。如果相邻两个特征点具有足量的共同轨迹，则认为这两个道路特征点之间存在路段，可以连接形成道路段。路网生成结果如图8所示。

图8 路网Fig.8 Road Network

部分道路拓扑关系表见表2。

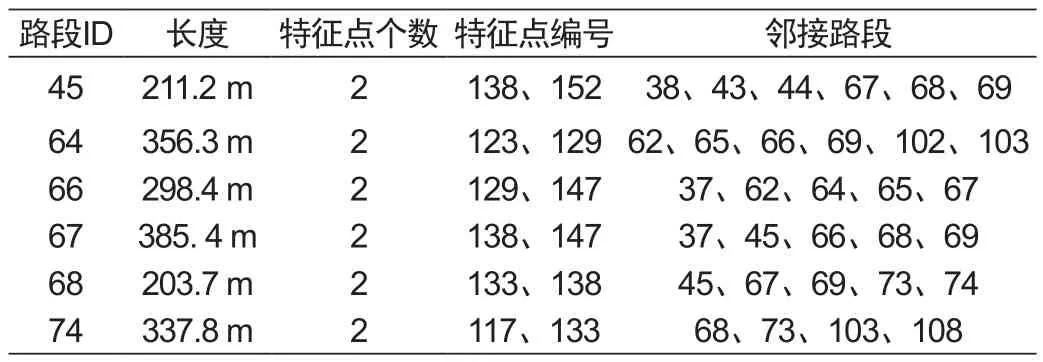
表2 道路拓扑关系表Tab.2 Road topological relation table

2.4 结果分析

本文的数据是2010年的浮动车轨迹数据，参考路网的矢量数据为2008年的数据，通过匹配判别，可以看出提取路网的准确性。如图9所示，通过比较，可以发现提取得到的道路交叉口和路网数据具有较好的一致性，有些没有匹配成功的道路，一是存在一些变动过的道路，如新增道路或者废弃道路等，二是存在一些错误相连的道路，三是存在数据覆盖率不足的原因。其中，错误相连的道路情况如图10所示。

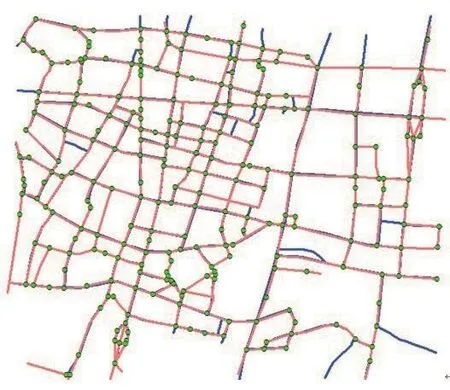
图9 对比分析Fig.9 Comparative analysis

图11 中转向口B与交叉口A和C相邻接，但是由于路段AB、BC都较短，因此，当车辆从A快速行驶至C时，会忽略B的存在，认为交叉口A和C是直接相连的，且存在路段，因此会生成错误的不存在的路段[6]。

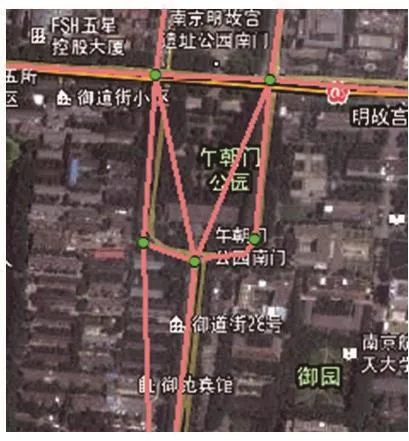
图10 错误关联道路Fig.10 Wrong connected road

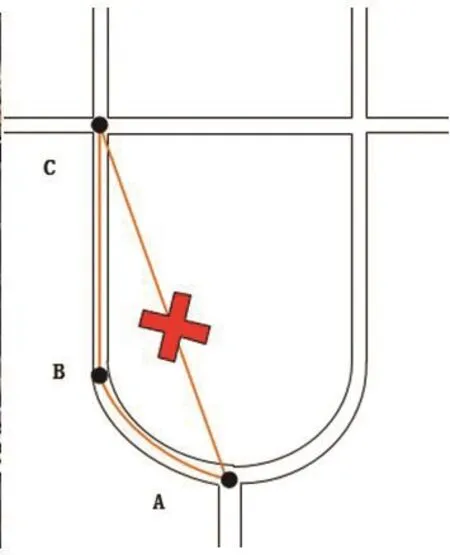
图11 示意图Fig.11 Illustration

3 结束语

随着车载定位设备的普及应用，车辆轨迹数据的来源越来越丰富。尤其是出租车的轨迹数据具有覆盖面广、信息更新速度快等特点。利用车辆轨迹构建的道路网络，可更新现有电 子地图的道路信息。本文将基于网格密度影响因子的多密度聚类算法引入路网提取，在实验区范围内取得了不错的结果，但是由于实验数据较少，而且没有考虑立交桥，高架等复杂道路情况。在以后的研究中，这些复杂路况也会成为我们研究的重点。