走进压轴题的“一线三等角”
江苏省南京金陵中学河西分校 李玉荣 (邮编:210019)
走进压轴题的“一线三等角”
江苏省南京金陵中学河西分校 李玉荣 (邮编:210019)
1 基本模型
文[1]、[2]把下面一个几何基本图形称为“一线三等角模型”:
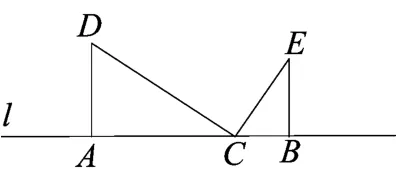
图1
如图1,直线l上有三点A、B、C,且 ∠DAC=∠DCE=∠CBE=90°,则△DAC∽ △CBE.特别地,当DC=CE 时,△DAC≌△CBE.我们把具有此特征的图形称为“一线三等角模型”.
2 中考压轴题
例1(2017年扬州卷)如图2,已知正方形ΑΒCD的边长为4,点Ρ是ΑΒ边上的一个动点,连接CΡ,过点Ρ作ΡC的垂线交ΑD于点Ε,以ΡΕ为边作正方形ΡΕFG,顶点G在线段ΡC上,对角线ΕG、ΡF相交于点Ο.
(1)若ΑΡ=1,则ΑΕ=_________________;
(2)①求证:点Ο一定在 △ΑΡΕ的外接圆上;
②当点Ρ从点Α运动到点Β时,点Ο也随之运动,求点Ο经过的路径长;
(3)在点Ρ从点Α到点Β的运动过程中,△ΑΡΕ的外接圆的圆心也随之运动,求该圆心到ΑΒ边的距离的最大值.
分析(1)、(2)①、②略;
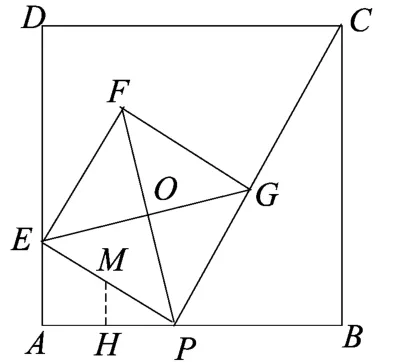
图2

备用图
(3)易知△ΑΡΕ的外接圆的圆心为PE的中点M,作MH⊥AB于H,产生“一线三等角模型”,圆心到ΑΒ边的距离为MH,求MH的最大值可借助二次函数求解.
解(3)取EP的中点M,则M为 △ΑΡΕ的外接圆的圆心,作MH⊥AB于H,则PA=2PH.
设PH=x,MH=y,则PB=4-2x,根据“一线三等角模型”知△MHP∽△PBC,得MH PB,即
例2(2017年南京卷)折纸的思考.
【操作体验】
用一张矩形纸片折等边三角形.
第一步,对折矩形纸片ABCD(AB>BC)(图①),使AB与DC重合,得到折痕EF,把纸片展平(图②).
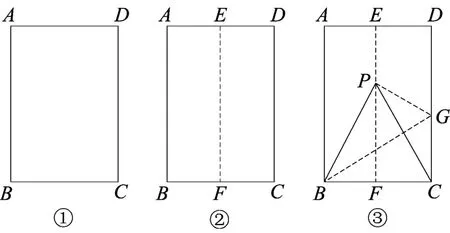
第二步,如图③,再一次折叠纸片,使点C′落在EF上的P处,并使折痕经过点B,得到折痕BG,折出PB、PC,得到△PBC.
(1)说明△PBC是等边三角形.
【数学思考】
(2)如图④.小明画出了图③的矩形ABCD和等边三角形PBC.他发现,在矩形ABCD中把△PBC经过图形变化,可以得到图⑤中的更大的等边三角形.请描述图形变化的过程.
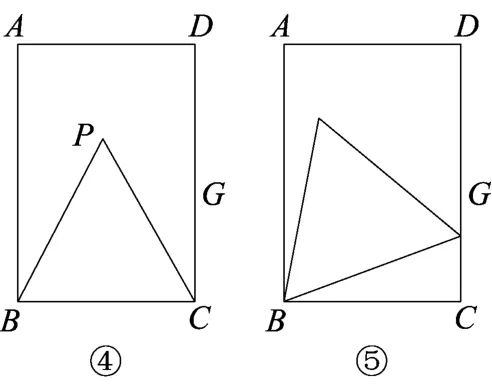
(3)已知矩形一边长为3cm,另一边长为acm.
对于每一个确定的a的值,在矩形中都能画出最大的等边三角形.请画出不同情形的示意图,并写出对应的a的取值范围.
【问题解决】
(4)用一张正方形铁片剪一个直角边长分别为4cm和1cm的直角三角形铁片,所需正方形铁片的边长的最小值为______cm.
分析(1)、(2)、(3)略;
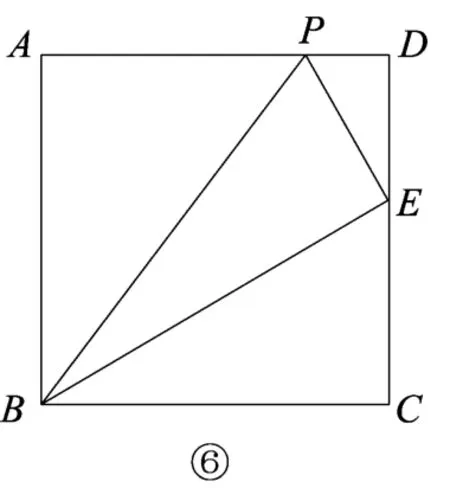
(4)由(2)、(3)积累的数学活动经验,可知点P落在AD上时,所需正方形铁片的边长最小,此时图中出现“一线三等角模型”.
解(4)如图⑥,点P在AD上,Rt△BPE中,∠BEP=90°,BE=4cm,PE=1cm.
例3(2017年无锡卷)如图,已知矩形ΑΒCD中,ΑΒ=4,ΑD=m.动点Ρ从点D出发,在边DΑ上以每秒1个单位的速度向点Α运动,连接CΡ,作点D关于直线ΡC的对称点Ε.设点Ρ的运动时间为ts().
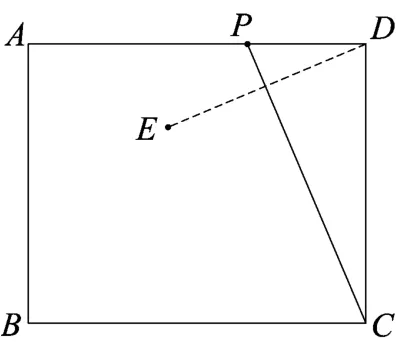
(1)若m=6,求当Ρ、Ε、Β三点在同一直线上时对应的t的值.
(2)已知m满足:在动点Ρ从点D到点Α的整个运动过程中,有且只有
一个时刻t,使点Ε到直线ΒC的距离等于3,求所有这样的m的取值范围.
分析(1)略;
(2)此题需分两种情形,找到点P的极端位置(与点A重合),求出AD的值,即可解决问题:①如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.②如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3,两种情况都与“一线三等角模型”密切相关.

图2
解(2)如图2中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3.
作EG⊥BC于G,延长GE交DA于F.则EG=3,CE=DC=4,
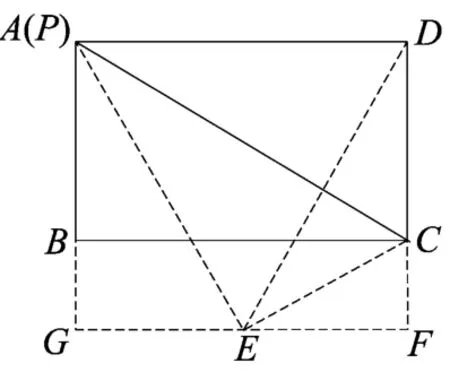
图3
如图3中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.
作EF⊥DC于F,延长FE交AB于G.则CF=BG=3,AG=7,所以
根据“一线三等角模型”知△PGE∽△ECF,
解得GE=37,即AD=GF=47.
综上所述,在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,这样的m的取值范围
例4(2017市台州卷)在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根,比如对于方程x2-5x+2=0,操作步骤是:
第一步:根据方程系数特征,确定一对固定点A(0,1),B(5,2);
第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点A,另一条直角边恒过点B;
第三步:在移动过程中,当三角板的直角顶点落在x轴上点C处时,点C的横坐标m,即为该方程的一个实数根(如图4);
第四步:调整三角板直角顶点的位置,当它落在x轴上另一点D处时,点D的横坐标为n即为该方程的另一个实数根.
(1)在图5中,按照“第四步“的操作方法作出点D(请保留作出点D时直角三角板两条直角边的痕迹);
(2)结合图4,请证明“第三步”操作得到的m就是方程x2-5x+2=0的一个实数根;
(3)上述操作的关键是确定两个固定点的位置,若要以此方法找到一元二次方程ax2+bx+c=0(a≠0,b2-4ac≥0)的实数根,请你直接写出一对固定点的坐标;
(4)实际上,(3)中的固定点有无数对,一般地.当m1、n1、m2、n2与a、b、c之间满足怎样的关系时,点P(m1,n1),Q(m2,n2)就是符合要求的一对固定点?
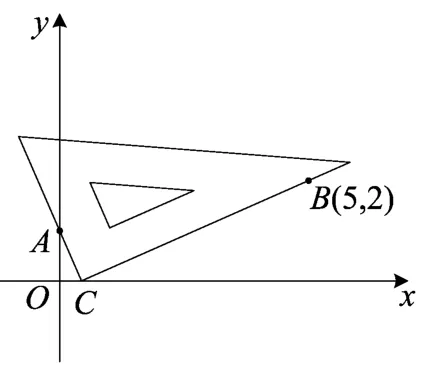
图4
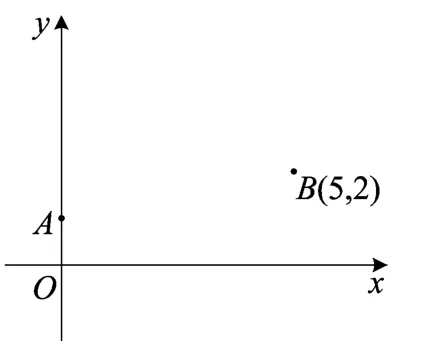
图5
分析(1)略;(2)根据∠ACB=∠AOC=90°,联想到过点B作x轴的垂线构造“一线三等角模型”,将问题转化为相似三角形求解,在此基础上领悟方法,即可解决问题(3)、(4).
解(1)略;
(2)证明:在图6中,过点B作BD⊥x轴,交x轴于点D.
根据“一线三等角模型”,知△AOC∽△CDB.
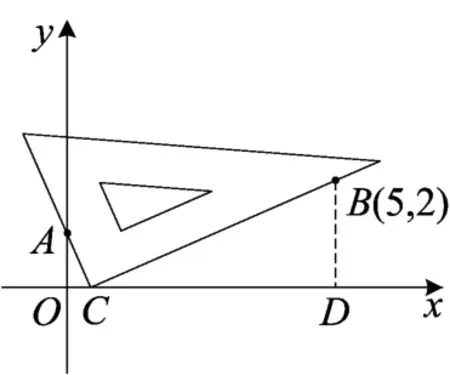
图6
所以m是方程x2-5x+2=0的实数根.
(3)方程ax2+bx+c=0(a≠0)可化为x2+,模仿研究小组作法可得:A(0,1),或等.

图7
(4)以图7为例:P(m1,n1)、Q(m2,n2),
设方程的根为x,根据“一线三等角模型”,利用相似三角形得,上式可化为x2-(m1+m2)x+m1m2+n1n2=0.又ax2+bx+c=0,即
3 教学启示
(1)数学是关于数和形的科学,形是数学的重要表现形式,学习数学离不开对几何图形的研究,《义务教育数学课程标准》在几何学习方面的要求是“能从较复杂的图形中分解出基本图形,并能分析其中的基本元素及其关系,利用直观来进行思考”.可见从复杂图形中“离析”出基本图形是学生必须具备的重要能力之一,也是解决几何问题的重要方法.同时数学也是关于模式的科学,这反映在数学解题时,需要进行模式识别,需要建构标准的模型,当我们面对一个陌生的、看似复杂的几何问题时,往往都可以将它转化为已经解决过的、较熟悉的、简单的几何图形.这里用到的基本图形就是解决问题的一个模式,用基本图形来分析、解决问题,是解题的常用方法、通用方法,可以发挥数学教学的长期效益,因此,必须重视基本图形在解题中的作用.
(2)教学中的基本图形一般分为两种:一种是教材中的定义、定理所对应的图形——单一型基本图形;另一种基本图形是例题或习题所对应的图形——复合型基本图形,它是单一型基本图形内容的扩展与延伸,它常常把一些重要的、常用的图形加入到单一型基本图形成为复合型基本图形的一部分.学生对单一型基本图形通常较为熟悉,用得比较得心应手,而对于复合型基本图形,虽然知道图形与结论,但解题时却常常忽略它的存在,导致解题困难或失败.为什么单独把这些复合型基本图形提出来,学生马上就能知道结论,而解题时为什么却熟视无睹?这就要求我们在教学过程中,一方面应重视基础知识、基本技能、基本方法的教学,注重对知识的发生、发展过程的揭示;另一方面,要注重对这些基本图形的提炼,要引导学生研究这些看似不起眼的复合型基本图形,分析基本图形的特征,深刻掌握基本图形,再精选相关的习题给学生练习,进一步理解基本图形的性质都是以怎样的方式发挥作用.
(3)罗增儒教授在《数学解题引论》中指出:学习数学的过程中,所积累的知识经验经过加工,会得出有长久保存价值或基本重要性的典型结构与重要类型——模式,将其有意识地记忆下来,当遇到一个新问题时,我们辨认它属于哪一类基本模式,联想起一个已解决的问题,以此为索引,在记忆储存中提取相应的方法来加以解决,这就是模式识别的解题策略.因此,在平时的教学中,应该培养学生对一些基本题型和基本图形的敏锐观察力,借给学生一双“数学慧眼”.在每学习一部分课本内容后,可以尝试以“专题讲座”的教学模式,引导学生自主探索、自我总结、逐步提高,对课本的这部分中的例题、习题加以提炼并深刻研究,形成结论储备起来,达到“见到图形,想到性质.想到性质,想全图形”的要求,在头脑中形成系统完备的待用“基本图形库”,最终把基本图形当作利刃,用到解题中去.
总之,教师在平时的教学和复习中,要寻找一些具有“广阔发展前景”的教材例题、习题或数学素材,深入研究,形成模型,探索利用模型解决问题的方法,启迪学生的数学思维,培养学生的创新意识,提升学生的思想素养,从而提高中考复习效率.
1 王元友.基于“一线三等角模型”的创新能力综合题设计[J].中国数学教育(初中版),2012(5)
2 周礼寅.一线三等角模型的建立与应用[J].中国数学教育(初中版),2012(10)
2017-06-26)
——《认识直角》教学片断与解读

