傅里叶变换下的直方图均衡化图像特征识别算法的研究∗
樊颖军
傅里叶变换下的直方图均衡化图像特征识别算法的研究∗
樊颖军
(陕西工业职业技术学院 咸阳 712000)
针对当前众多的智能识别系统中,通常需要通过一定的数学算法来实现一些特定的智能控制和模式识别,使得研发出来的产品具备较高的智能化程度。论文提出了傅里叶变换下的直方图均衡化图像特征识别算法的研究。通过对傅里叶算法的原理进行分析,明确了傅里叶变换在提取图像频谱信息时的作用;然后对图像频谱信息进行研究,确定了图像频谱图与识别特征的关系;接着对直方图均衡化的方法进行了分析,研究了利用直方图均衡化对图像中特征进行识别的实现方法。最后,对论文所设计的图像特征识别算法进行了实验结果分析,表明了论文所设计的特征识别算法具有较高的识别准确率。
图像特征识别;傅里叶变换;频谱图;直方图均衡化;模式识别
AbstractIn view of the current large number of intelligent recognition systems,it is usually necessary to achieve some specif⁃ic intelligent control and pattern recognition through a certain mathematical algorithm,which makes the products have a high degree of intelligence.In this paper,a histogram equalization algorithm is proposed based on Fourier transform.Through the analysis of the principle of Fourier transform,it is clear that the role of Fourier transformin extracting the spectrum information of the image.Then the spectrum information of the image is studied,and the relationship between the image spectrum and the recognition feature is de⁃termined.Then,the method of histogram equalization is analyzed,and the realization method of image recognition based on histo⁃gram equalization is studied.Finally,the experimental results of the image feature recognition algorithm designed in this paper are analyzed,which shows that the feature recognition algorithm designed in this paper has a high recognition accuracy.
Key Wordsimage feature recognition,fourier transform,spectrum map,histogram equalization,pattern recognition
Class NumberTG292
1 引言
随着科学技术日新月异的发展,图像特征识别技术已在诸多领域得到了应用,例如:医学检测分析、航空航天、遥感探测、森林火灾防护等[1]。当今社会智能化无处不在,在众多的智能化系统中模式识别是其不可或缺的一部分,而图像特征识别又是模式识别的重要实现方法,故图像特征识别已成为智能识别系统研究领域中的一项研究热点[2]。
对此,本文提出了傅里叶变换下的直方图均衡化图像特征识别算法的研究。首先,通过对傅里叶算法的原理进行分析,研究了图像的幅度谱、相位谱和功率谱信息的获取方法;然后对图像频谱信息进行研究,分析了图像频谱与识别图像中高、低频信息的关系,接着对直方图均衡化的方法进行了分析,研究了利用直方图均衡化对图像中特征进行识别的实现方法;最后通过实验分析表明了本文所设计方法具有较高的识别准确率。
2 傅立叶算法原理
在数字图像处理,科学家们提出了好多种适用于不同领域的数字图像变换方法,如小波变换,K-L变换等,其中傅立叶变换是图像处理中最常见,也是最重要的一种数字图像变换方法。
在1982年,Fourier在“热传导理论”中提出,一个任意的周期函数都可以分解为无穷多个不同频率的正弦信号之和,即傅立叶级数,求解傅立叶级数的过程即为傅立叶变换。设一维信号 f(x),则傅立叶变换公式为[3]
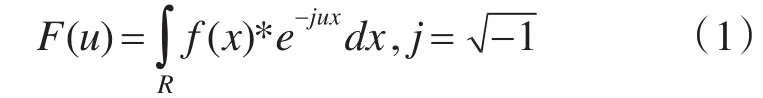
二维傅立叶变换在现代数字信号处理领域具有非常重要的地位。根据其算法的基本原理可以知道:在时域上任何连续测量的时序或信号,都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理创立的傅立叶变换算法就是利用直接测量到的原始信号,并且以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位信息[4]。
二维图像傅立叶变换的数学意义是将非周期的离散矩阵变换成一系列的周期离散矩阵,而其物理意义是将空间域的图像亮度值分布转化为图像的频域分布,即频谱图[5]。傅立叶变换为数字信号和数字图象处理提供了另一种分析方法。
对于二维图像而言,假设该图像大小为M*N,则图像即为周期的M*N离散信号,傅立叶变换类型为2-DFT,其表达公式如下[6]:
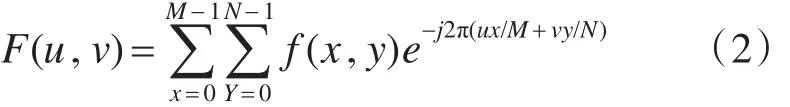
其中 u=0,1,2,…,M-1;v=0,1,2,…,N-1,且u,v为频率值。x,y为空域中的频率值,M 和N为数字图像的尺寸大小。由上公式可以看出,数字图像经傅立叶变换后,频域周期信号也为M*N大小。
傅立叶变换具有正交性、移位以及奇、偶、虚、实对称等性质,同时在时域和频域中满足循环卷积定理。
假设 x(n)、y(n)、h(n)均是 N点序列,相应的DFT 为 X(n)、Y(n)、H(n)。
如果有:

则有

对于DFT而言,工程人员在实际的应用中主要问题在于傅立叶算法的变换速度,在此以一维离散傅立叶变换为例[7]:

其中 k=0,1,2,…,N-1。
在实际使用时,为求出式(5)中N点的 X(k)需要N2次复数乘法和N(N-1)次的复数加法。若N=256,则需要运算65536次复数乘法和65280次复数加法,而这仅仅是对于一维信号的傅立叶变换的计算量。而对二维的数字图像而言,尤其是高分辨率的数字图像,其算法的运算量更为惊人,所以就需要更为快速的傅立叶算法。在1965年,快速傅立叶算法提出后,N点的X(k)复数乘法运算量从 N2降为N/2*log2N,仍然以N=256为例,复数乘法的计算量仅为1025,为原来计算量的1.56%[8]。图1为 FFT与 DFT所需运算量与计算点数的关系曲线。在图1中可以明显地看出FFT算法的优越性[9]。
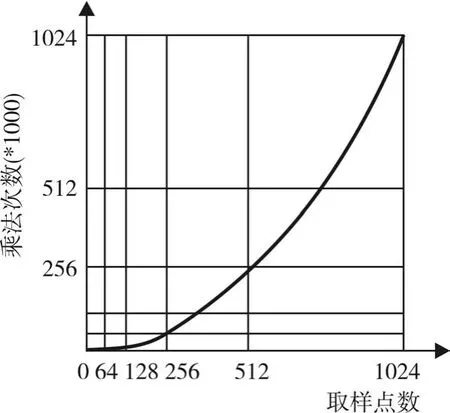
图1 FFT与DFT所需运算量与计算点数的关系曲线
自此,特别是现代计算机的发展,快速傅立叶变换得到了快速发展。也推动了快速傅立叶变换在数字图像处理中的广泛应用。
在实际的工业应用中,数字图像经过快速傅立叶变换后,可以得到三种频谱图,即频谱、相位谱和功率谱[10]。其频谱数学描述方式如下:
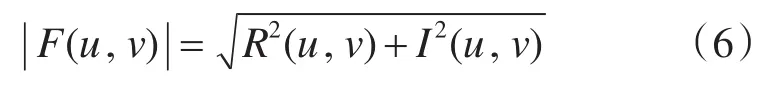
其相位谱数学描述方式如下:
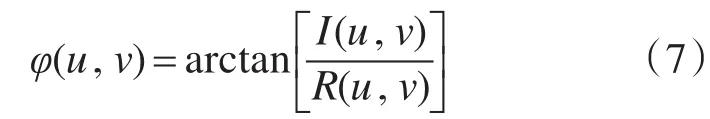
其功率谱数学描述方式如下:

其中R2(u ,v )与 I2(u ,v)是图像经过傅立叶变换后的实部和虚部。
由以上三个公式可知,图像信号经过快速傅立叶变换之后能够得到图像的幅度谱、相位谱和功率谱信息。而频谱图中的频率特性是表示图像中灰度变化剧烈程度的指标,功率谱图则反映了图像各个频率段的分布情况。
3 频谱描述
图像的频谱信息反映的是数字图像中各个频率在整个图像中的分布情况,图像信号经过傅立叶频谱变换后,其频谱分布规律是:随着频率从低到高,能量分布则从大到小,且图像的频谱图以直流所对应的频谱分量为中心分布。频谱图像中的直流分量反映的是数字图像中的平均亮度。如大面积的沙漠在数字图像中就是一幅色彩单一且变化缓慢的区域,对应的频率值很低;而相比较于那些地表属性变换剧烈的区域,如城市遥感图像,则其对应的高频率含量较大。从物理效果看,二维傅立叶变换是将数字图像从时间域转换到频率域,即分析其频域特性来提取该图像的时域特征。从另一个角度讲,傅立叶变换的本质是将图像的灰度分布函数通过二维傅立叶变换为图像在频域上的分布函数,从而实现从频域的角度去分析和提取图像的时域特征。
设图像 f(x ,y),其像素大小为M*N,则其图像的均值为[11]
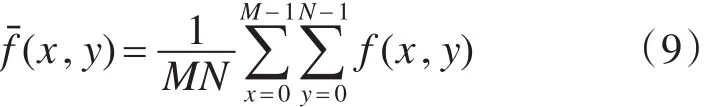
经过傅立叶变换后,图像的频谱途中直流分量的频率是u=0,v=0。由傅立叶变换公式可知:
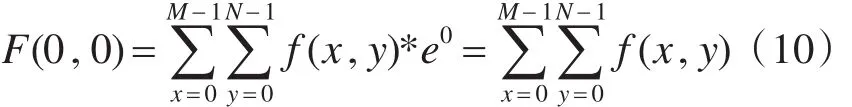
即:
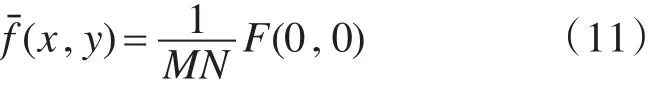
由上述公式可知,图像的能量频谱在坐标(0 ,0)点的幅值即为图像直流分量的值,为原图像所有像素点亮度均值的M*N倍。
通过研究傅立叶变换原理可以得知,频谱图中的低频成分主要反映原数字图像的色调信息。而频谱图中的高频部分反映的是原图像的边缘、噪声和纹理等信息。若采集到的图像信号变化比较平缓,没什么色彩的剧烈变化,比如说沙漠、海洋、成片的森林等。则该图像经过频谱变换后所得频谱图的低频分量较大,高频分量较小。若采集到的图像有很多结构性的纹理,边缘变化比较明显,例如城市遥感图像、风景区图像等。则该图像经过傅立叶变换得到的频谱图像中,高频分量占比比较大。在此以森林图像为例,具体分析图像的频谱特征。如图2所示。

图2 森林图像频谱分析图
从图中可以得知,图像的频谱图中有一条亮度明显的数值线。这是由于原图像中的山区与背景天际接壤处是明显的横向线,而原图像中在竖直方向无剧烈变化部分,故在频谱图中无水平方向的亮线。并且在图像频谱变换中,亮线分布方向与原图像中地物分布情况垂直。
4 直方图均衡化

其中T(r)要满足条件:(0≤T(r)≤1)。
而应用于数字图像的离散形式中,变换函数T(r)与原函数概率密度函数 pr(r)之间的数学关系式为

在本文中,需要将图像中的林火区域进行增强处理,以便后续处理器更能区别图像中的林火部分。在此以直方图均衡化的方法来实现图像的区域增强。直方图均衡化是一种利用灰度变换自动调节图像对比度质量的方法,其基本的变换原理是通过灰度级的概率密度函数求出灰度变换函数,简单的说就是把一概率分布已知的数字图像通过特定的变换方式,变成一幅概率分布均匀的数字图像。使得后续处理更加方便。其中在连续随机变量为基础的情况下,变换函数T(r)与原函数概率密度函数 pr(r)之间的数学关系式为[12]
其中(0≤rj≤1 k=0,1,2,…,L-1)。
在数字图像处理中,数字图像直方图均衡化的一般步骤为[13]
1)通过下式求出待处理数字图像的直方图。
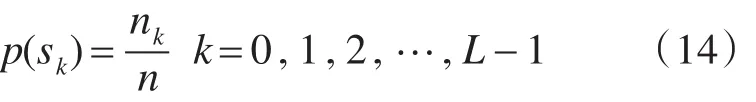
2)利用累计分布函数对原数字图像的统计直方图做变换,得到新的图像灰度。
3)进行近似处理,将新的灰度图取代旧的灰度图。同时将灰度值相等或相近的灰度直方图合并在一起,从而完成数字图像直方图均衡化。
在实际的图像变换过程中,首先统计出原始图像的灰度分布,然后利用傅里叶变换计算出原始数字图像的直方图分布,最后根据直方图灰度分布函数对原始图像的像素进行一一变换,即可实现对原始图像的均衡化。
5 实验结果与分析
文中以一林火图像为例,展示数字图像直方图均衡化的效果。其对比如图3和图4所示。
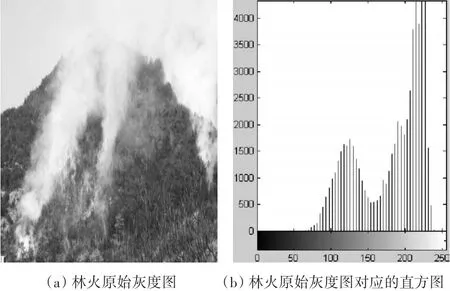
图3 林火灰度图与直方图
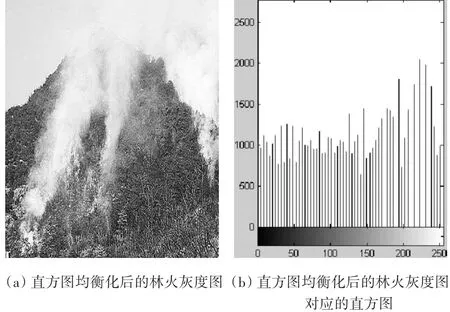
图4 直方图均衡化后的林火灰度图与直方图
由上述实验效果可以看出,数字图像经过直方图均衡化后明显提高了数字图像的对比度。图中的烟雾和火焰区域更加明显,突出了图像的边缘特征。这为接下来的图像频谱分析和图像数字滤波起到了很大的作用。
6 结语
本文提出了傅里叶变换下的直方图均衡化图像特征识别算法的研究。首先,通过对傅里叶算法的原理进行分析,利用傅里叶变换提取图像的频谱信息,然后对图像频谱信息进行研究,确定了图像频谱图与识别特征的关系,接着对直方图均衡化的方法进行了分析,利用利用直方图均衡化对图像中特征进行识别的实现方法。实验结果分析表明,本文所设计的特征识别算法具有较高的识别准确率。
[1]唐俊,邓立苗,陈辉.基于机器视觉的玉米叶片透射图像特征识别研究[J].中国农业科学,2014,47(3):431-440.
TANG Jun,DENG Limiao,CHEN Hui.Research on Maize Leaf Recognition of Characteristics from Transmission Im⁃age Based on Machine Vision[J].Scientia Agricultura Si⁃nica,2014,47(3):431-440.
[2]谭颖,刘技恒.远程采集无人机图像的特征识别方法研究[J].计算机测量与控制,2015,23(3):1005-1007.
TAN Ying,LIU Jiheng.Remote Collection and Character⁃istic of UAV Image Recognition Method Research[J].Computer Measurement& Control,2015,23(3) :1005-1007.
[3]温芝元,曹乐平.椪柑果实病虫害的傅里叶频谱重分形图像识别[J].农业工程学报,2013,29(23):159-165.
WEN Zhiyuan,CAO Leping.Citrus fruits diseases and in⁃sect pest recognition based on multifractal analysis of Fou⁃rier transform spectra[J].Transactions of the Chinese So⁃ciety of Agricultural Engineering,2013,29(23):159-165.
[4]黄静,孔令富,李海涛.基于傅里叶-隐马尔科夫模型的
人体行为识别[J].计算机仿真,2011,28(7):245-248.HUANG Jing,KONG Lingfu,LI Haitao.Human Behavior Recognition Based on HMM[J].Computer Simulation,2011,28(7):245-248.
[5]徐贵力,毛罕平.利用傅里叶变换提取图像纹理特征新方法[J].光电工程,2004,31(11):55-58.
XU Guili,MAO Hanping.A new method for extracting im⁃age texture features by Fourier transform[J].Opto-elec⁃tronic Engineering,2004,31(11):55-58.
[6]陈绵书,陈贺新,张春雨.基于离散傅里叶不变特征的人脸识别[J].计算机工程,2002,28(9):16-19.
CHEN Mianshu,CHEN Hexin,ZHANG Chunyu.Face Recognition Based on Fourier Scale Invariant Features[J].Computer Engineering,2002,28(9):16-19.
[7]朱丹丹,潘如如,高卫东.基于傅里叶特征谱和相关系数的织物疵点检测[J].计算机工程与应用,2014,50(19):182-187.
ZHUDandan,PANRuru,GAOWeidong.Fabric defect de⁃tection using characteristic spectrum of Fourier transform and correlation coefficient[J].Computer Engineering and Applications,2014,50(19):182-186.
[8]刘应钦,李红梅,白尚旺.基于圆谐-傅里叶矩与支持向量机的癌细胞识别[J].太原科技大学学报,2013,34(5):372-377.
LIU Yingqin,LI Hongmei,BAI Shangwang.Cancer Cell Identification Based on Circular Harmonic-Fourier Mo⁃ments with Support Vector Machines[J].Journal of Taiyu⁃an University of Science and Technology,2013,34(5):372-377.
[9]崔广才,窦凤平,王春才,等.基于傅里叶与局部特征结合的人体姿态识别方法研究[J].长春理工大学学报(自然科学版),2016,39(1):82-87.
CUIGuangcai,DOU Fengping,WANGChuncai,et al.Hu⁃man Behavior Recognition Method Research Based on Fourier Combined with Local Characteristics[J].Journal of Changchun University of Science and Technology(Natu⁃ral Science Edition),2016,39(1):82-87.
[10]方益明,郑红平,冯海林.基于傅里叶变换和独立成分分析的木材显微图像特征提取与识别[J].浙江林学院学报,2010,27(6):826-830.
FANG Yiming,ZHENG Hongping,FENG Hailin.Fea⁃
Research on Image Feature Recognition A lgorithm Based on Fourier Transform Coup ling H istogram Equalization
FAN Yingjun
(Shanxi Industrial Vocational College,Xianyan 712000)
TG292
10.3969/j.issn.1672-9722.2017.09.033
2017年3月10日,
2017年4月23日
樊颖军,男,硕士,讲师,研究方向:图像处理、计算机应用。

