基于间断有限元模型的给排水干湿分离研究∗

杨金英

基于间断有限元模型的给排水干湿分离研究∗

杨金英

（秦皇岛市山海关排水管理处 秦皇岛 066200）

针对给排水干湿分离难以确定运动交界的问题，该研究将利用离散格式有限元建立浅水方程模式，结合细分化单元内物理量进行线性重构，提出了一种新的给排水干湿分离方法。该方法保证了干湿交界处水体静止状态不被破坏，并且在水体非物理流动条件下的干湿处的过渡区域之间可连续。经过数值实验结果表明，采用间断式的有限元模式能够准确地模拟给排水的水体情形，计算过程中可精确计算间断间运动过程。

有限元模型；给排水；干湿分离；浅水方程

AbstractIn order to solve the problem that the movement boundary is difficult to be determ ined by the dry and wet separation of water supply and drainage，a new method of water and wet separation is proposed by using discrete finite element method to estab⁃lish the shallow water equation model and linear reconstruction with the physical quantities in the subdividing unit.The method can ensure that the static state of the water and wet junction is not destroyed，and can be continuous between the transitional areas of the wet and dry place under the non-physical flow condition of the water body.The results of numerical experiments show that the inter⁃mittent finite element model can accurately simulate the situation of water supply and drainage，and the process of intermittent mo⁃tion can be accurately calculated.

Key Wordsfnite element model，water supply and drainage，wet and dry separation，shallow water equation

Class NumberTN915.6

1 引言

有限元方法被广泛地应用于求解水体流动模型中，利用改进数值算法的形式将有限元划分与空间数阶相结合可以得到高精度的数值解［1～3］。在面对给排水工程项目时，间断有限元模型可通过浅水域模拟得到非结构化网格单元，确保了流体运动中的初始条件与流动边界的有机结合［4］。在模拟相流问题和激流问题过程中，传统的数值求解在处理强对流问题时易出现数值求解的耗散并导致模拟失真的结果［5］。间断有限元模型在模拟给排水这类间断性流体可避免连续性空间单元数值求解，因此本文为了研究给排水过程中的干湿分离技术，利用间断有限元模型分析水体浅水方程组，采用HLL函数的形式来对边界处数值的通量加以计算，结合水深非负算子对间断有限元模型进行Runge-Kutta格式化以提高算法精度，通过水体体积守恒定律对干湿处过渡进行数值分析。

2 间断有限元模型

2.1 浅水方程

在计算水体质量时采用固定网格的方法并且需要保证单元的拓扑关系稳定，由于基于水体质量守恒定律［6］，因此整个过程牵涉到的计算量较小。通常会采用一种线性近似方法来对单元内的水深进行重新构建［7］，以此达到干湿交接单元内水深为负的目的。但是采用上述的方法可能存在弊端，可能会造成水体自由表面计算错误，这样的情况就使得单元内的水体向周围邻近的单元内形成非物理性的流动，同时会导致单元内干湿交界面位置的计算错误［8］。采用上述的方法还会导致水体干湿界面捕捉困难的问题。存在这样的原因主要在于真实的界面有可能会存在于水体单元的内部而并非水体单元的表面或者交界处［9］。除上述情况之外，采用近似线性的薄层方法来处理，可能会使得浅水方程和谐性质遭到破坏，这样就无法对水体静止的情况进行模拟仿真，加大了研究的难度。即水体静止形式如下［10］

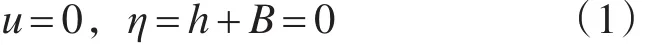
尽管列出了上述的一些局限性，大多数的研究仍然利用薄层方法对水体加以计算，因为其计算的量较小，且使用的条件和范围比较广泛，因此仍然能够广泛的应用于各种水体的浅水方程模型当中。

关于一维的水体浅水方程组，一般由两个方程所组成，一个方程用于描述水体的质量守恒，另一个方程用于描述物理动量恒等。用于描述能量守恒的方程形式如式（2），其中U代表能量守恒，F(U)代表流量项，S(U)代表源项等，对于方程中每一项的定义如式（3）。

在上式的描述中，关于水体的总水深用h表示，水体的水流速度用u表示，q=hu则表示能量守恒，动量用x表示，关于水体中的底坡的高程则利用b来表示。在水中的重力加速度用g来表示。为了方便研究的进行，在研究中我们将只考虑一种情况，即无粘情形，这样的情况适用于更加复杂的附加源项，类似于科氏力、底部摩擦项以及风应力等因素都将被考察在内。

2.2 间断有限元格式

为了对间断有限元格式加以应用，我们首先需要对域离散互不重合的区间Ωi=[xi-1/2，xi+1/2]加以计算。利用上述的域离散互不重合控制方程（4）乘以实验函数φ∈Vp(Ωi)，同时在不重合区间Ωi内进行积分的运算，则可以得到方程的弱解：

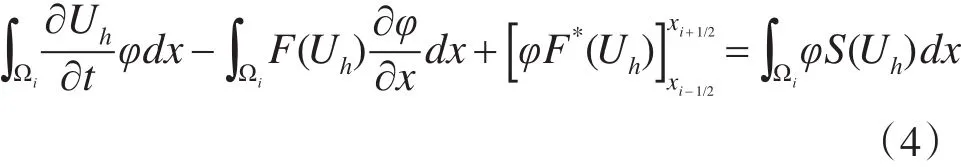
在上述的弱解形式中，Uh表示物理能量守恒变量的U的近似解。与实验函数φ类似，它们同属于解空间Vp(Ωi)内。在Ωi内，存在不超过 p的多项式共同组成了解空间Vp(Ωi)，这样的解空间使得多项式在单元的边界不连续成为可能。同时为了使得解空间内的单元间能够实现信息的交换和处理［11］，将利用数值通量 F*(Uh)来代替通量项F(Uh)。在本文的研究中，将采用HLL函数的形式来对边界处数值的通量加以计算［12］，同时为了获取到半离散的格式，本文中选用的基函数为Lagrang⁃ian函数［13］。利用上述提出的方法，我们将得到水体一维浅水方程的半离散化的形式，同时将其表示为常微分的形式，如下

一般情况下关于半离散形式的常微分方程，则能够实现二阶显式TVD Runge-Kutta格式化的计算，详细的推理过程如下

在推理的式中，Runge-Kutta的各个分步的系数一般用 βil以及αil来表示。Un以及Un+1则用于表示n以及n+1时刻的数值的解。通过对上述的模型采用TVB限制器，实现对于每一步数值的解的计算，同时还需要对数值振荡进行控制以保证数据的格式稳定。通过上述的公式与模型，我们最终能够得到空间精度的Runge-Kutta以及具有二阶时间的有限元间断浅水方程模型。

3 给排水干湿分离

3.1 水深非负算子

对于水深我们需要设定其为正值，因此本文将采用水深非负算子，并将其作用于每个Runge-Kut⁃ta的分步过程中［14］。为了方便研究的进行，我们需要对一些变量进行标识。Ui+=(hi+，q+i)用于表示非重复区间Ωi内的变量均值，Ui=(hi，qi)用于表示节点i∈{1，2 }处的解。其中非负算子的具体表达式如下

上式中，hmini表示非重复区间Ωi内的最小水深。根据上式的内容不难发现，对于所有的水深进行修正后得到的水深值都为非负数值。同时还能够保持水体单元内的总体积以及总动量不发生变化。关于水深的平均值为负的干单元，则需要将其平均水深重新修正为h+i=0。

3.2 干单元处理方法

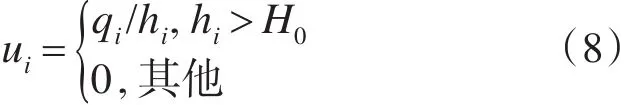
3.3 干湿处过渡

为了避免Gibbs现象的产生，本部分将采用对水体单元进行细分的方法实现对过渡单元的重新构建。完成干湿边界分区之后，将过渡的水体单元以及为节点分为两个子单元。同时为了使得干湿交界点的流速较小，也将以动量q为对象使用线性重构方法在子单元实现对动量的重新分布。细分后h与q在子单元的分布将如下所示。

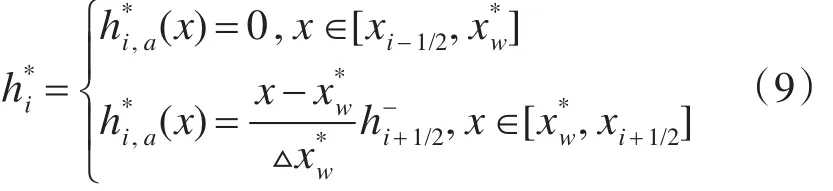
对于干湿过渡区域处于全湿状态的单元，这样的重新构建的过程要较为简单。全湿状态的单元底坡以及水体自由面所组成的形状为梯形形状。水深连续以及参照物理水体体积守恒定律，单元内水体深度的分布由以下公式确定：

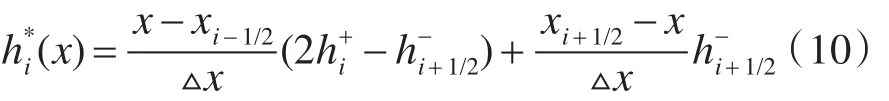
4 实验分析

在本部分的试验中，将不均匀底坡上水面静止的情况考虑在内，同时需要验证在干湿交界时模型对于水体数值的处理能够保持和谐的性质。设定[0，1]为计算域，同时需要将区间划分为100个均匀的小单元。底坡的高程如下式计算：

其中r=|x-0.5|，a的系数设定为1.3，rm的系数设为0.5。关于水体的初始水位高程则设定为η(x)=max(b(x)，1)，水体静止即速度为0。根据CFL的条件，时间步的长度取为0.0001s，而模拟2s后则计算过程结束，结果如图1所示。

图1 给排水干湿分离计算结果

由图1可见，对于干湿的处理方式有不同的方法，（a）与（b）为进行比较的结果。CONV为针对传统的线性重新构建方法得出的计算结果，HREF为针对满足和谐性质的干湿处理线性重新构建方法得出的计算结果。通过结果的对比显示，传统干湿处理方法无法对于水体的状态稳定下来，即无法保证水体的静止。如图1（b）所示，模拟2s后，在湿的单元内水体流入能够过渡到过渡单元内，从而使得动量q由干湿交界的单元向水深值较大的区域流动。同时对于新的干湿区域处理方法，通过将过渡的单元划分为干和湿两个部分，并使其保持连续，这样在动量q的计算过程中就能避免大量的舍入误差的产生。

5 结语

本研究主要围绕给排水过程中的干湿分离技术，以水体静止情形为出发点，利用间断有限元模型对离散互不重合的区间进行计算。采用HLL函数的形式对边界处数值的通量加以计算，同时，选用的基函数为Lagrangian函数得到水体一维浅水方程的半离散化的形式和二阶显式TVD Run⁃ge-Kutta格式化。运用水深非负算子和Lagrangian基函数作用于每个Runge-Kutta的分步。参照Lewy的限制条件将过渡的水体单元以及为节点分为两个子单元，使用线性重构方法在子单元实现对动量的重新分布。

［1］唐亮，凌贤长，艾哈迈德·艾格玛.液化侧向流动场地桩基动力反应振动台试验三维有限元数值模拟方法［J］.土木工程学报，2013（1）：180-184.

TANG Liang，LIN Xianchang，AIGema.Three Dimension⁃al Finite Element Numerical Simulation of Shaking Table Test for Dynamic Response of Pile Foundation in Lique⁃fied Lateral Flowing［J］.China Civil，2013（1）：180-184.

［2］鲁阳，邹建锋，郑耀.基于非结构网格的TTGC有限元格式的实现及在超声速流动中的应用［J］.计算力学学报，2013（5）：712-716.

LU Yang，ZOU Jianfeng，ZHANG Yao.Realization of TT⁃GC Finite Element Scheme Based on Unstructured Grid and Its Application in Supersonic Flow［J］.Chinese Jour⁃nal of Computational Mechanics，2013（5）：712-716.

［3］魏匡民，苏佩珍.有限元法中非关联流动条件下刚度矩阵的存储方式及平衡方程求解［J］.三峡大学学报（自然科学版），2011，33（5）：10-14.

WEI Kuangmin，SU Peizhen.Storing Method of Stiffness Matrix and Solving Equilibrium Equation in Non-associat⁃ed Flow Condition［J］.Journal of China Three Gorges Uni⁃versity Natural Sciences，2011，33（5）：10-14.

［4］张忠宇，姚熊亮，张阿漫.基于间断有限元方法的并列圆柱层流流动特性［J］.物理学报，2016，65（8）：1-11.

ZHANG Zhongyu，YAO Xiongliang，ZHANG Aman.Flow characteristics of parallel laminar flow based on discontin⁃uous finite element method［J］.Acta Physica Sinica，2016，65（8）：1-11.

［5］杨青远，周苏芬，卢伟真，等.明渠交汇水流阻力对平面二维数值模拟的影响［J］.水科学进展，2012，23（2）：236-242.

YANG Qingyuan，ZHOU Sufen，LU Weizhen，et al.Influ⁃ence of Flow Resistance in Open Channel Crossing on Two-dimensional Numerical Simulation［J］.Advances in Water Science.2012，23（2）：236-242.

［6］马鑫磊，任光明，夏敏.滑坡涌浪预测评价方法综述［J］.水利水电科技进展，2015（3）：89-98.

MA Xinlei，REN Guangming，XIA Min.Summarization of forecasting and evaluating methods of landslide surge［J］.Advances in Science and Technology of Water Resources，2015（3）：89-98.

［7］李艳华，丁建丽，闫人华.基于国产GF-1遥感影像的山区细小水体提取方法研究［J］.资源科学，2015，37（2）：408-416.

LI Yanhua，DING Jianli，YAN Renhua.Study on Extrac⁃tion of Small Waters in Mountainous Area Based on Do⁃mestic GF-1 Remote Sensing Image［J］.Resources Sci⁃ence，2015，37（2）：408-416.

［8］吴锋，钟万勰.浅水动边界问题的位移法模拟［J］.计算机辅助工程，2016，25（2）：5-13.

WU Feng，ZHONGWanxie.Displacement method for shal⁃low water dynamic boundary［J］.Computer Aided Engi⁃neering，2016，25（2）：5-13.

［9］王增辉，夏军强，李涛.两步计算模式下的三门峡水库异重流模拟［J］.四川大学学报（工程科学版），2016，25（2）：5-13.

WANG Zenghui，XIA Junqiang，LI Tao.Simulations of three-grade calculation of three-gorges reservoirs with density flow［J］.Journal of Sichuan University Engineer⁃ing Science Edition，2016，25（2）：5-13.

［10］程文龙，史英标，吴修广.基于AUSM+-UP格式的有限体积模型及其在钱塘江河口的应用［J］.水力发电学报，2013，32（3）：82-86.

CHENG Wenlong，SHI Yingbiao，WU Xiuguang.Finite Volume Model Based on AUSM-UPScheme and Its Ap⁃plication in Qiantang Estuary［J］.Journal of Hydroelec⁃tric Engineering，2013，32（3）：82-86.

［11］徐立云，荣巨，郭昆吾.基于改进粒子群算法的制造单元构建方法研究［J］.制造技术与机床，2014（3）：47-53.

XU Liyun，RONG Ju，GUO Kunwu.Research on Manu⁃facturing Cell Construction Based on Improved Particle Swarm Optimization［J］.Manufacturing Technology&Machine Tool，2014（3）：47-53.

［12］杨金波，李订芳，陈华.和谐WAF格式在带干河床浅水波方程中的应用［J］.华中科技大学学报（自然科学版），2012，40（2）：54-57.

YANG Jinbo，LI Dingfang，CHEN Hua.Application of Harmonic WAF Scheme in Shallow Water Wave Equa⁃tions with Dry Riverbed［J］.Journal of Huazhong Univer⁃sity of Science and Technology Natural Science Edition，2012，40（2）：54-57.

［13］李俊杰，张颖.高分子稀溶液的多尺度模型研究进展［J］.厦门大学学报（自然科学版），2013，52（2）：289-296.

LI Junjie，ZHANG Ying.Progress in Research on Multi⁃scale Models of Polymer Dilute Solution［J］.Journal of Xiamen University Natural Science，2013，52（2）：289-296.

［14］赵张益，张庆河，李世森.Runge-Kutta间断有限元格式在一维浅水方程中的应用［J］.水科学进展，2012，23（5）：695-701.

ZHAO Zhangyi，ZHANG Qinghe，LI Shisen.Application of Runge-Kutta Discontinuous Finite Element Scheme in One Dimensional Shallow Water Equation［J］.Advances in Water Science，2012，23（5）：695-701.

［15］刘存良，潘振宽，郑永果.两种保持符号距离函数的水平集分割方法［J］.吉林大学学报（工学版），2013，43（3）：115-119.

LIU Cunliang，PAN Zhenkuan，ZHENG Yongguo.Two Level Set Segmenting Methods for Preserving Symbol Dis⁃tance Function［J］.Journal of Jilin University Engineer⁃ing and Technology Edition，2013，43（3）：115-119.

Study on Dry and W et Separation of W ater Supp ly and Drainage Based on Discontinuous Finite Elem ent

YANG Jinying
（Drainage Administrative Department of Shanhaiguan District of Qinhuangdao City，Qinhuangdao 066200）

10.3969/j.issn.1672-9722.2017.09.043

2017年3月8日，

2017年4月23日

杨金英，女，硕士，高级工程师，研究方向：给排水方面。