初中数学如何解题快

杨中建

摘要：函数对中学生来说是一个比较难解决的数学问题，为了让学生更好，更快的解决这一问题，可让学生借助于一些简单的口诀来解决实际的函数图像问题，从而提高学生对数学学习的兴趣。

关键词：函数；口诀；解题；效率

一般的，要判定一个函数图像y=kx+b（k，b为常数且k≠0），都要经过列表、描点、连线等过程确定，最简单的也要用两点（-k/b，0）和（0，b）来确定。

为了便于记忆，根据k，b的正负性的四种情况的特点让学生将其总结为以下口诀：

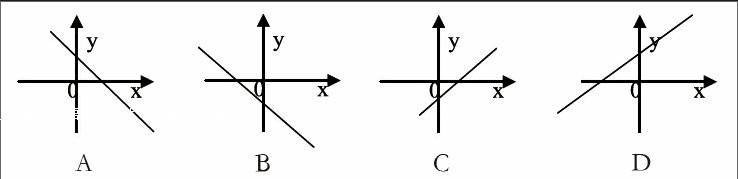
大大不经四，小小不经一，大小不经三，小大不经二，B在前K在后。如下图所示

一、根据解析式判定图像的位置。

例如：函数y=3x+2的图像，因为b=2>0，k=3>0，根据口诀：“大大不经四”可得，该函数不经过第四象限。同理可以用：“小小不经一”判定，y=-2x+（-5）的函数图像不经过第一象限；“大小不经三”判定，y=-8x+0.8的函数图像不经过第三象限；“小大不经二”判定，y=6x+（-2）的函数图像不经过第二象限。

二、根据图像判定解析式y=kx+b中k，b的符号。

如圖1：

函数图像未经过第三象限，根据：“大小不经三”可得b>0，k<0；

如图2：

函数图像未经过第一象限，根据：“小小不经一”可得；b<0，k<0

如图3：

函数图像未经过第二象限，根据：“小大不经二”可得；b<0，k>0

如图4：

函数图像未经过第四象限，根据：“大不经四”可得；b>0，k>0

三、口诀的灵活应用。

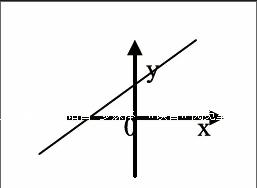
例如：已知y=kx+b（k，b为常数且k≠0）的图像如图五所示则y=bx+k的图像为（）。

图五：

分析：观察函数图像图五，未经过第三象限，根据“大小不经三”可得b>0，k<0，现需判定y=bx+k的函数图像，因为b，k符号可以确定，根据b，k的符号，用口诀“小大不经二”加以判定答案为C。

让学生学会综合运用所学的知识和方法解决简单的实际问题，加深对所学知识的理解，获得运用数学解决问题的思考方法。综合起来能培养学生这几方面的能力：一是收集信息、整理信息的能力；二是利用所学知识解决实际问题的能力等。更要的是，在数学实践活动中，学生经历观察、操作、总结、验证、推理等活动，在实践的过程中，获得了良好的情感体验，感受数学知识间的相互联系，体会定理、口诀等在数学的作用。促进学生全面、持续和谐地发展。这是21世纪拔尖人才所必须的素质，也是《数学课程标准》所倡导的新的学习方式。学科实践活动作为一种新的学习内容及方式，对于我们来说是一个崭新的课题。在实践和探索中我们认识到，学生的学习不仅是知识的积累，更应在知识应用中强调灵活应用的意识；不仅要让学生主动地获取知识，还要让学生去发现和研究问题；不仅要让学生运用知识解决实际问题，更要在寻求问题解决的过程中激发学生的创新潜能，感悟学习思想和方法。endprint