基于承诺的可验证公平性微支付

刘忆宁 赵全玉



基于承诺的可验证公平性微支付

刘忆宁*①②赵全玉①

①(桂林电子科技大学数学与计算科学学院 桂林 541004)②(桂林电子科技大学广西可信软件重点实验室 桂林 541004)

微支付交易具有交易量极大且单次交易额极小的特点，使得复杂的认证协议不适用于微支付。Micali等人(2002)提出的基于概率选择微支付方案，把微支付聚合成宏支付，大幅提高了微支付的效率。Liu-Yan在(2013)提出了保证所有参与者的数据融入概率选择结果的生成, 而且使得所有参与者可以验证结果的公平性。然而，Liu-Yan方案中银行可能获得额外利益，从而破坏了协议的公平性。该文首先分析了Liu-Yan方案的安全威胁，并且以“1个用户-1个商家”的模型代替Liu-Yan方案中“大量用户-1个商家”的模型，以数据承诺技术为基础保障结果的公平性与可验证性。

微支付；承诺；公平性；可验证性

1 引言

电子支付方案是电子交易中实现各方支付信息正确、安全、保密进行的规则和约定，通常包含3方参与：用户(U)，商家(M)，银行(B)[1]。电子支付方案分为宏支付和微支付方案，宏支付交易金额较大、安全性要求高，通常使用数字签名、公钥加密等实现安全性；微支付交易金额小、效率性要求高，支付金额甚至远远小于支付能耗的成本。微支付交易对效率性要求高，因此并不能照搬宏支付方案来实施。

微支付是实现电子交易实时支付的一种技术[2]，应用非常广泛，如流量收费，歌曲下载等。交易所需支付的金额小，如果每次交易都采用常规计费方式(身份认证等)代价太大。微支付交易在满足一定安全性前提下，要求交易过程尽量简单，通讯能耗尽量低。因此微支付的一些性质被提出，如：安全性，高效性，隐私性[9]，公平性[10,11]等。

1997年，Rivest等人[12]提出基于Payword的高效微支付方案，但在该方案中，商家无法聚合不同用户的微支付进行兑换。Rivest基于概率选择的微支付[13]中，大量用户和商家共同选择一个用户支付账单，实现大量用户的微支付以较小概率转化成某一用户的宏支付，如：每次交易时1000个用户和商家共同选择一个用户，每个用户被选中的概率是0.001，那么每个用户平均1000次交易中有一次被选中，被选中后需要支付之前的账单。但文献[13]存在两个弱点：(1)如何保证用户被选择的公平性；(2)如何防止用户超额支付。文献[14]提出MR1, MR2, MR3。MR1保证了用户和商家公平的选择用户，但存在用户超额支付的情况；MR2解决了超额扣除用户金额的风险，但恶意用户和商家会合谋攻击银行；MR3把计算中心转移到银行，但并未解决超额扣除的问题。另外在MR2和MR3中，用户使用私钥对每次交易进行签名并发送给商家，可能会泄露用户身份，破坏协议的隐私性。同时数字签名计算比hash链和对称加密更加复杂，影响在移动终端中的使用。

Liu-Yan(2013)提出一种基于hash函数[15,16]和插值多项式的微支付方案[17]。该方案使用插值多项式生成可验证性随机数来选择支付用户，保护了隐私性，降低了计算负担。但该方案存在安全威胁。银行可以定向的选择用户, 谋取非法利益；另外，Liu-Yan方案很难实现大量用户同步操作，而且用户数增加时，计算负担会大幅度增加。本文提出基于承诺的可验证公平性微支付方案，商家和用户利用承诺协同生成一个小概率的结果，而且用户可以验证这个结果的公平性，该方案不仅满足其他安全特性，还具有更好的公平性。

2 Liu-Yan方案

2.1 Liu-Yan方案

在Liu-Yan方案中，有3个参与者：用户(U)，商家(M)，银行(B)，分为4个阶段：注册阶段，支付阶段，概率选择阶段，验证阶段。在方案中，每次交易值为1分，每个用户以的概率被选中去支付其账单，每次交易都在1000个用户中选择一个用户。

(1)注册阶段：

(3)概率选择阶段：

2.2 Liu-Yan方案的分析

Liu-Yan方案中被选择去支付的用户U和M都可以验证是否参与生成，但其安全性存在风险。1000个用户中一些用户的账单，另外一些, B每次选择其中一个用户支付账单，而给商家充值1000分。

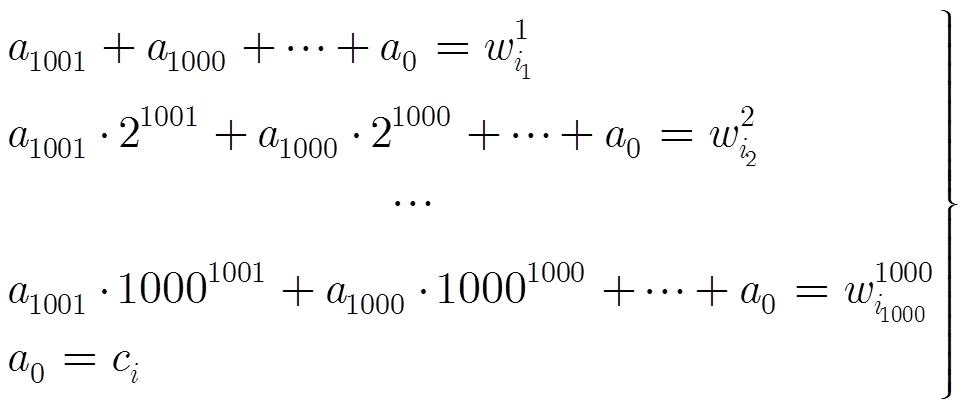
表1 次选择得到账单大于1000分用户的概率

表1 次选择得到账单大于1000分用户的概率

(次数)123456 概率1/23/47/815/1631/3263/64

在Liu-Yan方案中，需要大量用户同步共同选择一个进行宏支付的用户，同步性要求太强，限制了方案的实用性。现实生活中更多是用户和商家之间的双方交易，如果每次选择1000个用户来生成多项式，交易时间不统一会使得完成交易的时间大幅度增加。Liu-Yan方案中假设用户为1000个，则需要生产一个1001次多项式。现实生活中单笔商品或服务的价格极低，但交易量极大的微支付交易越来越多，也就需要更多用户的微支付才能以更小概率转化成某一个用户的宏支付，生成的多项式次数更高，计算复杂度增加，使得交易的开销大幅提升。为了降低计算复杂度，提高交易效率，降低同步性，并且防止银行通过选择特定用户来谋取利益，本文提出基于承诺的可验证公平性微支付方案。

3 基于承诺的可验证公平性微支付方案

3.1 承诺

承诺方案是密码学领域中的一个重要工具, 承诺函数的性质使承诺在零知识证明，安全多方计算，身份认证等方面得到广泛的应用。通常承诺方案应满足两个目标：

满足以上目标的承诺方案很多，其至少应该包括：承诺阶段和打开阶段。假设承诺双方为Alice, Bob，承诺阶段：Alice根据承诺函数计算，并将发给Bob。打开阶段：当Alice需要打开承诺，Alice公布消息, Bob可以验证承诺值是由生成的。

3.2 基于承诺的可验证公平性微支付方案

基于承诺的可验证公平性微支付方案中，有3个参与者：用户(U)，商家(M)，银行(B)，对应的公钥、私钥分别为：,,。本文以hash函数作为承诺函数，这不影响基于其它承诺方案微支付协议的各项安全性质。交易过程分为4个阶段：注册阶段(与Liu-Yan方案相同)、概率选择阶段、支付阶段、验证阶段。具体步骤如下：

4 效率性及和安全性分析

4.1 效率性分析

微支付的效率性包括计算效率和通讯效率，没有使用复杂的数字签名进行认证的协议是高效的。方案中可验证性随机数生成的主要运用hash运算，采用分层结构运算，大幅度降低了整体的计算量。本方案根据自己选择的随机数来生成可验证性随机数，降低了用户验证随机数的计算量，在普通的移动终端上也可以瞬间完成。

假设1000个人需要和商家完成交易，每个人和商家交易1000次，那么每人有一次被选中支付账单。假设1000个被选中的人中有1个人要求验证参与生成，比较Liu-Yan方案和本文方案中1000人每人交易1000次的总的计算量和通讯量，发现签名运算的次数、生成hash链的条数、验证hash运算的次数和数据通讯量相差不大。本文方案在生成的时间和验证阶段计算上有很大优势，比较结果如表2所示。

表2 1000人每人交易1000次生成R的时间和验证阶段计算比较

由表2可知：本文方案在计算时间和验证计算上更加高效。另外Liu-Yan方案中用户人数成倍数增加时，生成可验证性随机数的计算负担大幅度增加。利用电脑参数为：系统：Ubuntu 14.04.3LTS, CPU: 2.50 GHz，内存：8 G的电脑分别计算生成可验证性随机数的时间，得到表3。本文中hash函数以SHA-256为例。

表3 生成可验证性随机数R的时间(ms)

4.2 安全性分析

4.2.1 SVO逻辑语法和公理 安全性分析是安全协议的基本组成部分，本文利用SVO逻辑对方案进行安全性分析。SVO逻辑定义了消息语言和公式语言。以,和分别表示消息，公钥和私钥，P和Q表示协议的实体。在消息语言中，以表示消息。表4中介绍SVO逻辑使用的符号。

表4 SVO逻辑语法的符号说明

4.2.2 SVO逻辑的形式化分析

(1) SVO逻辑对安全协议给出了4种安全目标：

(2)初始化假设：

(3)协议分析：

(3)

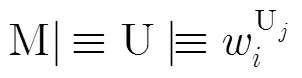
(5)

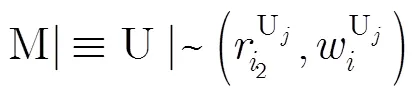
(7)

(9)

4.2.3 公平性分析 公平的目的在于确保协议参与各方的地位和作用平等，参与各方拥有的能力是相同的。微支付协议公平性指参与者在任何时刻都不会得到特别的好处。

命题2 本文方案对U, M和B都是公平的。

在Liu-Yan方案中，B可以特定选择用户，从中谋取利益，对U和M是不公平。在本文方案中U, M和B都是公平的参与交易，所以本文方案比Liu-Yan方案具有更好的公平性。 证毕

5 结束语

本文对Liu-Yan基于插值多项式的微支付方案进行分析，提出了基于承诺的可验证公平性微支付方案。在本文方案中，用户和商家利用承诺协同生成概率验证性的结果，决定用户是否需要支付之前账单。用户和商家都可以验证是否参与生成结果，和Liu-Yan方案相比，本文方案除了满足安全性、隐私性、可验证性和高效性外，还具有更好的公平性。

[1] YANG Chingnung and WU Chihcheng. MSRC: Micropayment scheme with ability to return changes[J]., 2013, 58(1/2): 96–107. doi: 10.1016/j.mcm.2012.07.010.

[2] 王涛, 姚松涛, 郭荷清. 安全微支付技术应用于分布式系统安全审计的研究[J]. 通信学报, 2005, 26(5): 118-121.

WANG Tao, YAO Songtao, and GUO Heqing. Research on the application of secure micropayment technology in security auditing of distributed system[J]., 2005, 26(5): 118-121.

[3] GHAFOORI Z, DEHGHAN M, and NOURHOSEINI M. PPayWord: A Secure and Fast P2P Micropayment Scheme for Video Streaming[M]. Springer International Publishing Switzerland, Springer International Publishing, 2014: 79-91. doi: 10.1007/978-3-319-10903-9_7.

[4] HWANG Shinjia. Security Flaws of Off-Line Micro Payment Scheme with Dual Signatures[M]. Springer Science Business Media Dordrecht, Springer Netherlands, 2014: 905-909. doi: 10.1007/978-94-007-7262-5_103.

[5] CHA Byungrae, LEE Sanghun, PARK Soobong,Design of micropayment to strengthen security by 2 factor authentication with mobile and wearable devices[J]., 2015, 109(7): 28-32. doi: org/10.14257/astl.2015.109.07.

[6] DECKER C and WATTENHOFER R. A Fast and Scalable Payment Network with Bitcoin Duplex Micropayment Channels[M]. Springer International Publishing Switzerland, Springer International Publishing, 2015: 3-18. doi: 10.1007/ 978-3-319-21741-3_1.

[7] CHEUNG Helen and YANG Cungang. A secure electronic payment protocol for wireless mesh networks[J]., 2014, 6(5): 1-22.doi: 10.5121/ijnsa.2014.6501.

[8] YEN Sungming, LIN Hsichug, CHEN Yenchang,PayStar: A denomination flexible micropayment scheme[J]., 2014, 259: 160-169. doi: 10.1016/ j.ins.2013.07.031.

[9] BIRYUKOV A and PUSTOGAROV I. Proof-of-Work as Anonymous Micropayment: Rewarding a Tor Relay[M]. Springer Verlag Berlin Heidelberg, Springer Berlin Heidelberg, 2015: 445-455. doi: 10.1007/978-3-662-47854-7_27.

[10] 樊利民, 廖建新. 公平的移动小额支付协议[J]. 电子与信息学报, 2007, 29(11): 2599-2602.

FAN Limin and LIAO Jianxin. Fair mobile micropayment protocol[J]., 2007, 29(11): 2599-2602.

[11] 万仁福, 李方伟, 朱江. 一种适用于移动环境的认证和支付协议[J]. 电子与信息学报, 2005, 27(3): 498-501.

WAN Renfu, LI Fangwei, and ZHU Jiang. An efficient authentication and payment protocol for mobile communication[J].&, 2005, 27(3): 498-501.

[12] RIVEST R L and SHAMIR A. Payword and micromint: Two simple micropayment scheme[C].International Workshop on Security Protocols, Springer-Verlag, 1997, 1189: 69-87. doi:10.1007/3-540-62494-5_6.

[13] RIVEST R L. Electronic lottery tickets as micropayments[C]. International Conference on Financial Cryptography, Springer Berlin Heidelberg, 1997: 307-314. doi:10.1007/ 3-540-63594-7_87.

[14] SILVIO M and RIVEST R L. Micropayment Revisited[C]. Topics in Cryptology CT-RSA 2002, Springer Berlin Heidelberg, 2002: 149-163. doi: 10.1007/3-540-45760-7_11.

[15] RAFAEL M, HOMERO T, JOEL R,. P2PM-pay: Person to person mobile payment scheme controlled by expiration date[J]., 2015, 85(1): 289-304.doi: 10.1007/s11277-015-2738-y.

[16] LIU Yining, HU Lei, and LIU Heguo. A micropayment scheme based on weighted multi-dimensional hash chain[J].(), 2006, 23(5): 791-794. doi: 10.1007/s11767-005-0219-2.

[17] LIU Yining and YAN Jihong. A lightweight micropayment scheme based on Lagrange interpolation formula[J]., 2013, 6(8): 955-960. doi: 10.1002/sec.643.

[18] SAZE G. Generation of key pre-distribution schemes using secret sharing scheme[J]., 2003, 128(1): 239-249. doi: 10.1016/S1571-0653(04)00173-8.

Verifiable Fairness Micropayment Scheme Based on Commitment

LIU Yining①②ZHAO Quanyu①

①(,,541004,)②(,,541004,)

Due to the large transaction number and tiny value in micropayment, it is not practical to authenticate each transaction. Micali. (2002) propose a lottery-based micropayment to integrate multiple micropayment to one macro-payment that is worth using complicated authentication. Liu-Yan scheme (2013) guarantees the result is verifiable by involving all participants’ data. However, there still exists a flaw that the malicious bank maybe obtain the illegal benefit by controlling the specific purchaser not be selected to execute the macro-payment, moreover, this attack can not be detected. In this paper, the flaw is firstly described, then, an improved version is proposed. Specifically the model “multiple purchasers to 1 merchant”in Liu-Yan’s scheme is replaced with a new model “1 purchaser to 1 merchant”, which guarantees the fairness and verifiability for all using the commitment technique.

Micropayment; Commitment; Fairness; Verifiability

TP309

A

11009-5896(2017)03-0743-06

10.11999/JEIT160300

2016-03-31；改回日期：2016-07-29；

2016-10-09

刘忆宁 ynliu@guet.edu.cn

国家自然科学基金(61363069, 61301166, 61662016)，桂林电子科技大学研究生教育创新计划(2016YJCX44)，广西研究生教育创新计划(YCSZ2015149)

The National Natural Science Foundation of China (61363069, 61301166, 61662016), The Innovation Project of GUET Graduate Education (2016YJCX44), The Innovation Project of Guangxi Graduate Education (YCSZ2015149)

刘忆宁： 男，1973年生，教授，博士，博士生导师，主要研究方向为轻量级安全协议.

赵全玉： 男，1989年生，硕士生，研究方向为微支付协议、电子投票协议.