基于圆柱绕流直径压强差的二维风测量方法

刘 成 赵 湛 杜利东 方 震



基于圆柱绕流直径压强差的二维风测量方法

刘 成①②赵 湛*①杜利东①方 震①

①(中国科学院电子学研究所 北京 100190)②(中国科学院大学 北京 100049)

基于流量传感器的圆柱结构2维风传感器，其测量性能对地面风测量而言不够准确。由此，该文通过分析风洞实验数据，建立一种数学模型来描述圆柱绕流中直径两端压强差的分布，并根据该模型提出一种通过检测该直径压强差来计算风速风向的2维风测量方法。对风洞测试数据应用该方法，在2~40 m/s风速范围内，风速计算值误差不超过±(0.2+0.03 V) m/s，风向计算值误差不超过±5°。相比使用流量传感器的圆柱结构2维风传感器，该方法提高了测量准确度。同时，该方法不需要转动部件，不受机械摩擦和惯性的制约，需要占用的空间小。

2维风测量；圆柱绕流；直径压强差；风速风向

1 引言

风速和风向是气象观测中的重要参数。在地面风测量中，风速矢量基本可以被认为是2维矢量[1]，在大部分实际使用的场合中，风速矢量也基本是平行于某个平面[2]，因此2维风的测量具有实用意义。传统的旋转式2维风速计有转动部件，需要占用较大的空间，同时性能受机械磨擦和惯性的制约。应用MEMS技术能够使2维风传感器满足日益增多的新需求。热学原理的单片风传感器是MEMS 2维风传感器的一个研究热点[3]，能大大降低传统热学原理风传感器的功耗[2,4]，适合低速[5]、低密度[6,7]空气的流速测量。但这类传感器的敏感元件直接接触气流，脆弱的敏感元件没有得到较好保护[2,8]，在对鲁棒性有要求的应用场合中需要额外的保护结构[9]。

通过特定形状物体在受到风作用时表面压强分布的规律来测量风，可以使敏感元件不必直接接触被测气流。得到广泛应用的五孔皮托管利用了这种原理，但只能测量一定角度范围内的风[10]。文献[2]于2009年首次提出利用圆柱的直径两端压强差来测量2维风速矢量的思路，设计分支管路将这一压强差转化为流量，再使用热学原理MEMS流量传感器来测量这一流量，进而计算出风速风向。在近似处理不同雷诺数对压强分布的影响时，文献[2]提出的方法引入了12%的误差。文献[11]在文献[2]的基础上，制作了圆柱形2维风传感器的原型机，在风洞中测试其风向测量误差不超过。文献[12]对圆柱形2维风传感器的设计作了改进，在风洞中测试其风速测量相对误差8%，风向测量误差。相比于自动气象站风速测量误差±(0.5+0.03 V) m/s和风向误差的水平[1]，这一测量准确度有待提高，其中表示指示风速。

不同圆柱绕流状态下圆柱表面压强分布有明显差异，上述基于流量传感器的方法在近似处理这一差异时引入了较大的误差。由于使用热学原理MEMS流量传感器来间接测量圆柱直径两端压强差，存在流过MEMS敏感部分的气流，且流量测量对管路结构敏感。针对上述问题，本文建立了一种数学模型来描述圆柱绕流中圆柱直径两端压强差分布，并根据此模型提出一种基于圆柱绕流直径压强差的2维风测量方法。该方法在风洞测试中表现出了更高的测量准确度。同时该方法不需要转动部件，不受机械摩擦和惯性的影响。

2 理论基础

利用直径压强差测量2维风的方法，涉及到流体力学的圆柱绕流问题，常用压强系数来描述圆柱表面压强分布，其定义[13]为

(2)

式(2)表明，圆柱任意一条直径的两端压强相等。由于流体的粘性，圆柱表面压强实际分布与理想情况有明显差异，直径两端压强不一定相等。使用雷诺数来判断流体的流动状态，其定义[14]为

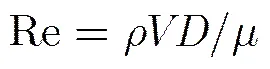
在通常雷诺数情况下，阻风圆柱一条直径的两端之间存在压强差。如图1所示，本文定义圆柱绕流中阻风圆柱直径两端压强差为该直径正端与负端的压强之差。则可定义压强差系数为

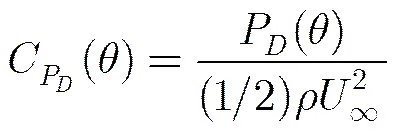
在雷诺数约350~1×105范围内，圆柱受风阻力与动压的比值随雷诺数的变化较为平缓，并在雷诺数1×104~1×105范围内几乎不变；如果高于此雷诺数范围，圆柱受风阻力急剧下降[15]。这一阻力是由圆柱两端压强差引起的，说明在此雷诺数范围内，压强差系数分布受雷诺数影响较小。本文方法的远期目标是测量高至60 m/s的风，如果此风速在标准空气条件下对应雷诺数为1×105，则圆柱的直径为26.04 mm。如果圆柱尺寸小于此值，圆柱受风阻力在雷诺数1×104~1×105范围内的良好特性不能被充分利用。

3 测量方法设计

3.1 风洞实验

为了测量圆柱绕流中直径压强差的实际分布，在FS-003一级标准风洞中进行实验。实验使用金属圆柱，表面抛光为亮光泽面，其上开有8个测压孔。测压孔直径应尽量小以准确测量某一角度处的压强；受限于加工条件，本文采用1 mm孔径，在圆柱上对应圆心角。测压孔内部通过管道与压差传感器相连，测量4条直径的两端压强差，这4条直径相互间隔。根据本文第2节的描述，圆柱的直径采用26 mm。

记录风洞中标准皮托管风速计示数为参考风速，同时记录的还有气温和气压。被测阻风圆柱固定在一个角度计圆盘上，随角度计一起转动，通过角度计示数可以读出各条被测直径的方位角。皮托管在被测圆柱上游约30 cm处[16]，并且与被测圆柱上的测压孔不在同一高度，以避免相互影响。

实验中测量了11个风速点，从3.6 m/s到34.0 m/s又回到3.1 m/s，对应雷诺数范围5.1×103~5.7×104，动压范围5.5~680 Pa，温度范围21°C~ 26°C，气压范围101.9~102.4 kPa。在每个风速点，选定的一条直径的方位角，从0°开始，在60°内以5°步长、在60°外以10°步长扫描了360°范围。压差传感器的读数以4 Hz的采样率输出，在每一种风速和方位角的组合下记录4个压差传感器各约50个样本，并按照结构对称性将对应相同方位角的来自不同压差传感器的数据整合。在测试风速范围内，阻风圆柱下游漩涡具有规则性和周期性[1,17,18]，使用时间平均的方法计算平均值。整理出的阻风圆柱直径两端压强差系数的平均值如图2所示。

从图2(a)可以看出，不同雷诺数下，阻风圆柱直径两端压强差系数随直径方位角的分布基本一致，特别是在范围内。此分布呈现出非单调性，在约65°附近达到最小值。图2(b)是对压强差系数分布的另一种表示，当直径方位角固定，此直径对应的压强差系数在雷诺数5.1×103~5.7×104范围内基本保持不变。

3.2 建立模型

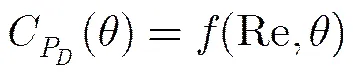
(6)

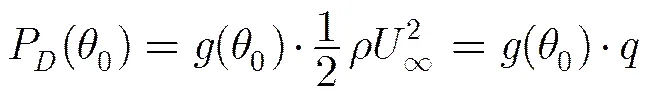
(8)

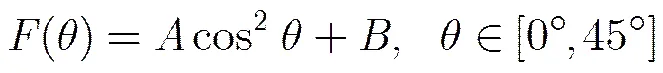
(10)

此即为描述圆柱绕流中圆柱直径两端压强差的数学模型。

图2 压强差系数测量值与雷诺数和方位角的关系

图3 对压强差系数与方位角关系的拟合

表1 对直径压强差与流体动压之间关系的线性拟合结果

值(°)051015202530354045 值1.47691.47211.43521.34591.23561.07220.9163 0.72210.5173 0.3429 值0.14140.42590.26200.82190.94480.61950.4668-0.17770.3992-0.3543 拟合优度1.00001.00001.00000.99990.99991.00001.0000 0.99991.0000 1.0000

3.3 测量方法

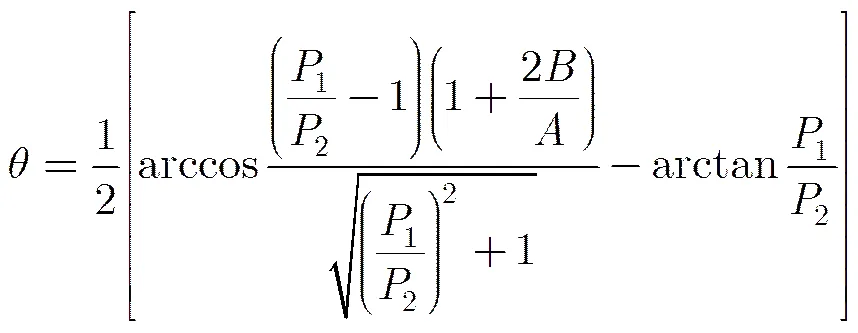
(12)

4 实验验证

为验证提出的测量方法的可行性，将其应用在建模时使用的FS-003风洞数据上。对每一风向情况，使用距离前驻点分别为和的两点的测试数据作为计算的已知量。每个风速点下，风速计算值按风向进行平均，结果如图4(a)所示；每种风向情况下，风向计算值按风速进行平均，结果如图4(b)所示。图中同时给出了计算值相对实际值的误差，平均风速相对误差不超过2%，平均风向误差不超过，证明了此测量原理在雷诺数范围5.1 ×103~5.7×104内的可行性。

为进一步验证提出的测量方法原理的可行性，衡量其性能，设计制作了相应原型机[20]，在另一台F-03风洞中进行测试。该风洞工作段截面尺寸320 mm×320 mm，可调风速范围0.5~45 m/s，紊流度不大于0.5%。在2.1~39.1 m/s风速范围内选择了7个风速点，对应雷诺数范围3.55×103~6.85×104，环境温度19°C~20°C，气压100.8~102.5 kPa。每个风速点下，以步长扫描范围的风向。在每一测试点，以4 Hz采集4个测压孔的压差数据各约100个样本，并按对称性将整合数据，计算平均值。按照和上文相同的计算方法，计算结果如图5和图6所示。

图5(a)是风速计算值按风向进行平均的结果，风速计算值与实际风速的相对误差绘制在图5(b)中，其相对误差不超过±5%。在风速10 m/s以上时，风速相对误差不超过±3%；在10 m/s以下时相对误差不超过5%，误差大小不超过(0.2+0.03 V) m/s。总体来说，风速误差小于(0.2+0.03 V) m/s。图6(a)是风向计算值按风速进行平均的结果，风向计算值与实际风向的误差绘制在图6(b)中，其误差不超过。F-03风洞测试数据的计算结果证明，本文提出的测量方法在雷诺数3.55×103~6.85×104范围内可行。

5 结束语

本文基于风洞实验数据，通过两次线性拟合建立了一种数学模型来描述圆柱绕流中阻风圆柱直径两端压强差的分布。根据该模型，本文提出了一种通过检测该压强差来计算风速和风向的2维风测量方法，该方法计算步骤简单，无需迭代。对FS-003风洞数据应用该方法，验证了其在雷诺数5.1×103~5.7×104范围内的可行性。对在另一台F-03风洞中获得的实验数据应用该方法，风速计算值误差不超过(0.2+0.03 V) m/s，风向计算值误差不超过5°，验证了该方法在雷诺数3.55×103~6.85×104范围内的可行性。该方法相比应用MEMS流量传感器的圆柱形2维风传感器的测量方法，近似处理引入的误差得到了降低。由于没有转动部件，该方法不受机械摩擦和惯性的制约，不需要占用较大的空间，本文所用圆柱形探头直径为26 mm。

压差传感器在测量直径压强差时，测压管路中几乎没有气流，测量性能对管路结构不敏感，制作传感器时对加工一致性的要求较低。从直观上来说，较小的气流能更好地保护内部的传感器敏感元件，将敏感元件与灰尘和雨水隔离。但灰尘和雨水仍有可能堵塞测压孔，影响测量准确度，这将是设计制作供现场测量使用的2维风传感器时需要解决的问题。

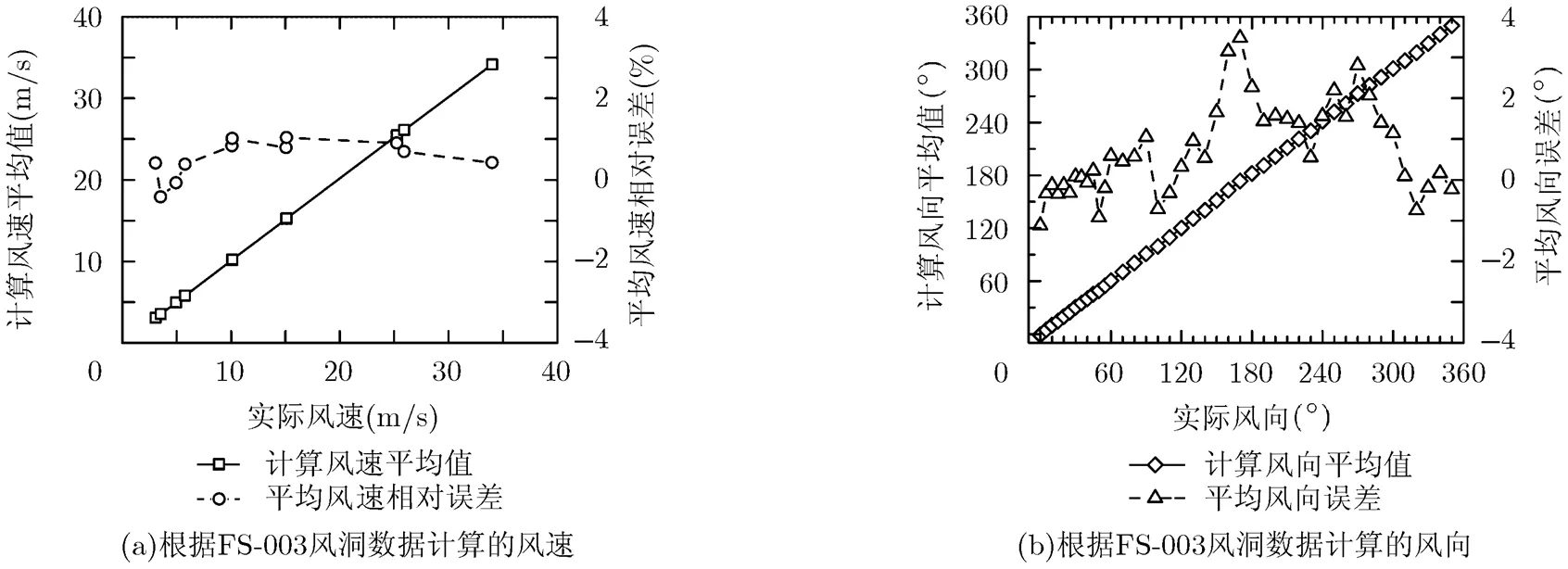
图4 根据FS-003风洞数据计算的风速和风向

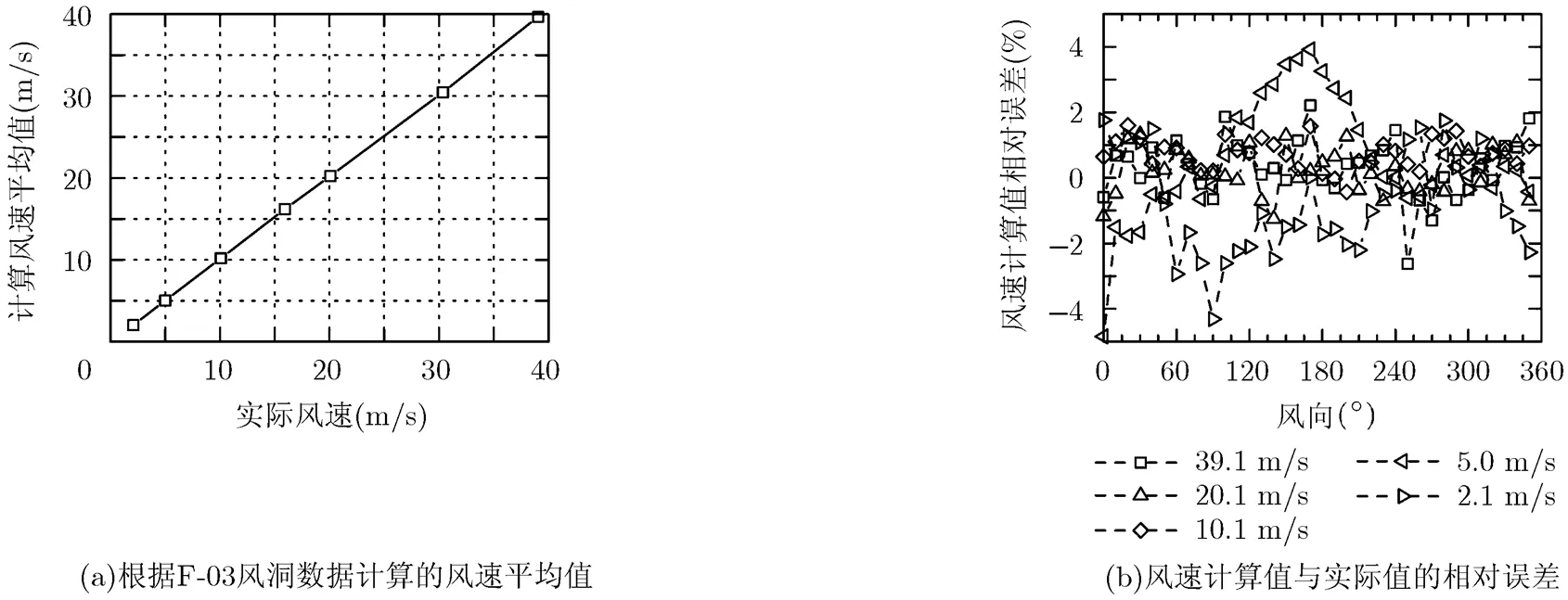
图5 根据F-03风洞数据计算的风速及其相对误差

图6 根据F-03风洞数据计算的风向及其误差

[1] 孙学金, 王晓蕾, 李浩, 等. 大气探测学[M]. 北京: 气象出版社, 2009: 172-247.

SUN Xuejin, WANG Xiaolei, LI Hao,. Atmospheric Observation[M]. Beijing: China Meteorological Press, 2009: 172–247.

[2] BRUSCHI P, DEI M, and PIOTTO M. A low-power 2-D wind sensor based on integrated flow meters[J]., 2009, 9(12): 1688–1696. doi: 10.1109/JSEN.2009. 2030652.

[3] ZHU Yanqing, CHEN Bei, QIN Ming,. 2-D micromachined thermal wind sensors--A review[J]., 2014, 1(3): 216–232. doi: 10.1109/ JIOT.2014.2319296.

[4] VERESHCHAGINA E, TIGGELAAR R M, SANDERS R G P,. Low power micro-calorimetric sensors for analysis of gaseous samples[J].:, 2015, 206: 772–787. doi: 10.1016/j.snb.2014.08.077.

[5] LIU Haobing, LIN Nay, PAN Shanshan,. High sensitivity, miniature, full 2-D anemometer based on MEMS hot-film sensors[J]., 2013, 13(5): 1914–1920. doi: 10.1109/JSEN.2012.2236014.

[6] KOWALSKI L, JIMENEZ V, DOMINGUEZ-PUMAR M,. Low pressure spherical thermal anemometer for space missions[C]. 2013 IEEE Sensors, Baltimore, Maryland, USA, 2013: 1–4. doi: 10.1109/ICSENS.2013.6688493.

[7] KOWALSKI L, ATIENZA M T, GORRETA S,. Spherical wind sensor for the atmosphere of Mars[J]., 2016, 16(7): 1887–1897. doi: 10.1109/JSEN. 2015.2509168.

[8] DONG Ziqiang, CHEN Jingjing, QIN Yukun,. Fabrication of a micromachined two-dimensional wind sensor by Au-Au wafer bonding technology[J]., 2012, 21(2): 467–475. doi: 10.1109/JMEMS.2011.2179014.

[9] ZHU Yanqing, CHEN Bei, GAO Di,. A robust and low-power 2-D thermal wind sensor based on a glass-in-silicon reflow process[J]., 2015, 22(1): 151–162. doi: 10.1007/s00542-015-2423-9.

[10] GEORGIOU D P and KYPROS F M. Fabrication and calibration of a sub-miniature 5-hole probe with embedded pressure sensors for use in extremely confined and complex flow areas in turbomachinery research facilities[J]., 2014, 39: 54–63. doi: 10.1016/j.flowmeasinst.2014.07.005.

[11] PIOTTO M, DEI M, PENNELLI G,. A miniaturized 2D solid state anemometer based on thermal flow sensors[J]., 2009, 1(1): 1463–1466. doi: 10.1016/j. proche.2009.07.365.

[12] PIOTTO M, PENNELLI G, and BRUSCHI P. Fabrication and characterization of a directional anemometer based on a single chip MEMS flow sensor[J]., 2011, 88(8): 2214–2217. doi: 10.1016/j.mee.2010.11.009.

[13] 张兆顺, 崔桂香. 流体力学[M]. 北京: 清华大学出版社, 1999: 167–168.

ZHANG Zhaoshun and CUI Guixiang. Hydromechanics[M]. Beijing: Tsinghua University Press, 1999: 167–168.

[14] SCHLICHTING H. Boundary-Layer Theory[M]. 7th Edition, New York: McGraw-Hill, 1979: 12–23.

[15] ZURELL Cory. Aerodynamics of a circular cylinder inclined to airflow and wind-induced vibrations of dry, inclined cables at high wind speeds[D]. [Ph.D. dissertation], University of Ottawa, 2004: 22–25.

[16] CARE I and ARENAS M. On the impact of anemometer size on the velocity field in a closed wind tunnel[J]., 2015, 44: 2–10. doi: 10.1016/j.flowmeasinst.2014.11.007.

[17] CHEN Wenli, LI Hui, and HU Hui. An experimental study on a suction flow control method to reduce the unsteadiness of the wind loads acting on a circular cylinder[J]., 2014, 55(4): 1–4. doi: 10.1007/s00348-014-1707-7.

[18] LYSENKO D A, ERTESVÅG I S, and RIAN K E. Large- eddy simulation of the flow over a circular cylinder at Reynolds number 2×104[J].,, 2014, 92(3): 673–698. doi: 10.1007/s10494-013- 9509-1.

[19] GIACOMO P. Equation for the determination of the density of moist air (1981)[J]., 1982, 18(3): 33–40. doi: 10.1088/0026-1394/18/3/011.

[20] LIU Cheng, DU Lidong, and ZHAO Zhan. A directional cylindrical anemometer with four sets of differential pressure sensors[J]., 2016, 87(3): 035105. doi: 10.1063/1.4943222.

Method of Measuring Two-dimensional Wind Based on Diametrical Pressure Differences Developed by Flow Around Cylinder

LIU Cheng①②ZHAO Zhan①DU Lidong①FANG Zhen①

① (Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China) ②(University of Chinese Academy of Sciences, Beijing 100049, China)

The cylindrical two-dimensional wind sensor employing flow meters is not accurate enough for surface wind measurement. By analyzing the data from wind tunnel experiments, a model is proposed to describe the diametrical pressure differences developed by the flow around a circular cylinder. A method is derived from the model for two-dimensional wind measurement by detecting the diametrical pressure differences. When the proposed method is applied to the data from wind tunnel tests in range of 2~40 m/s, the relative wind speed errors and the wind direction errors are no more than ±(0.2+0.03 V) m/s and ±5° respectively. The proposed method is more accurate than the cylindrical two-dimensional wind sensor using flow meters. Without moving parts, the method is immune to mechanical wear and inertia.

Two-dimensional wind measurement; Flow around a cylinder; Diametrical pressure difference; Wind speed and direction

TP212.1

A

11009-5896(2017)03-0737-06

10.11999/JEIT160468

2016-05-09；改回日期：2016-09-23；

2016-11-14

赵湛 zhaozhan@mail.ie.ac.cn

公益行业专项(GYHY201006044)，国家自然科学基金(51305423)

Special Fund for Public Welfare (GYHY- 201006044), The National Natural Science Foundation of China (51305423)

刘 成： 男，1990年生，博士生，研究方向为微传感器与系统集成以及风传感器.

赵 湛： 男，1958年生，研究员，研究领域为多传感器集成及微纳制造技术、无限传感器网络应用技术、生命信息感知与计算等.

杜利东： 男，1980年生，助理研究员，研究方向为微传感器系统与集成、无线传感器网络.

方 震： 男，1976年生，副研究员，研究领域为无线传感网、可穿戴技术、健康物联网.