大型机载相控阵雷达天线受扰分析
李艳艳 林中朝 张 玉 赵勋旺 路宏敏
大型机载相控阵雷达天线受扰分析
李艳艳 林中朝 张 玉*赵勋旺 路宏敏
(西安电子科技大学天线与微波技术重点实验室 西安 710071)
该文利用基于并行核外高阶矩量法的区域分解法(DDM)快速准确地分析了机载雷达相控阵的受扰特性。分析机载相控阵主波束相位扫描变化时,可将其分为机载平台和相控阵两个区域。由于机载平台不变,故在求解过程中只需计算一次,并利用核外技术将该部分的阻抗矩阵等相关数据信息存入硬盘。每改变一次扫描角,只需重新计算相控阵区域,进而结合已存储的机载平台区域,通过迭代便能得到机载相控阵的受扰特性。该方法能够大幅度降低大型机载问题的计算时间和存储需求。数值仿真实例表明,该方法可用于高效分析大型机载平台中的雷达相控阵天线布局问题。
相控阵雷达;区域分解法;高阶矩量法
1 引言
机载相控阵雷达(PAR)是航空电子系统中的重要组成部分。相控阵雷达于20世纪60年代问世,与传统的机械扫描雷达相比,它具有波束控制灵活、能够快速扫描及可实现多种工作方式多目标搜索和跟踪等优点,被广泛应用于地基、海基和空基等领域。近年来,随着我国经济和科技实力的提高,在相关领域也有了突破性进展,相继完成了两种机载有源相控阵雷达的研制,为我国下一代机的研制提供了强大的支撑。然而机载雷达的研制过程中,仅依靠实验测量手段,不仅要耗费大量的经费,且许多实际的情况不允许也难以实现精确的实验测量,同时还会大大延长研制周期。
随着国内高效能计算机的蓬勃发展,现代高性能电磁仿真技术为机载相控阵雷达等复杂系统的研制提供了高效的解决途径。目前比较常用的电磁数值方法有矩量法(MoM)、有限元(FEM)和时域有限差分(FDTD)等。其中MoM的高理论精度使其被广泛应用于电磁辐射和散射问题的仿真分析,然而在处理诸如机载平台等复杂电大系统问题时,会产生庞大的复数稠密矩阵,所需付出的计算存储资源与计算时间代价极高。尽管笔者所在团队在前期工作中已采用大规模并行计算技术大幅度提高了求解规模和速度[1],但在处理机载雷达天线布局问题时仍需耗费大量的计算资源和较长的计算时间。为此,本文提出一种基于并行核外高阶MoM的区域分解方法(DDM),通过一种“分而治之”的思想,将处于分离状态的机载平台和相控阵分为两个区域。当相控阵架设到飞机平台后,阵列主波束在方位面或俯仰面进行相位扫描时,机载平台不发生任何变化,因此在求解过程中只需被计算一次,然后利用核外技术将该部分的阻抗矩阵等相关数据信息存入硬盘中。每计算一次不同扫描角度,只需重新计算天线所在区域,并结合已存储的机载平台区域,通过区域间的迭代便能得到整个问题的解,这一方案能够快速高效地实现机载雷达天线的布局研究,给工程应用提供了一种可靠的方法。
2 高阶矩量法及区域分解算法
2.1 高阶矩量法
相对于传统的低阶RWG基函数矩量法,高阶基函数矩量法是定义在参数坐标系下的多项式组合函数,它通过合理调整多项式的阶数来表达电磁流相位变化,将网格边长的要求放松到1个波长左右[6,7]。一般只需约20个基函数就可以描述一个平方波长表面的电磁流,极大地减少了矩量法未知量的数目,降低了计算机资源消耗。高阶矩量法对金属和介质的表面采用双线性曲面进行几何建模。双线性曲面是一个非平面的曲面四边形,由4个顶点唯一地确定。参数方程可表示为
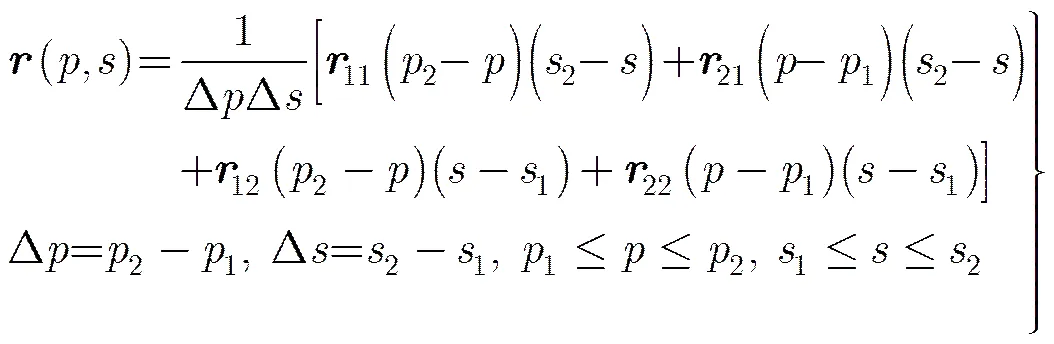
另外,高阶多项式基函数能够自动满足连续性方程,从而保证了金属介质连接区域的电磁流连续性[8]。以方向的分量为例,双线性曲面上的电流和磁流密度可以分别展开为
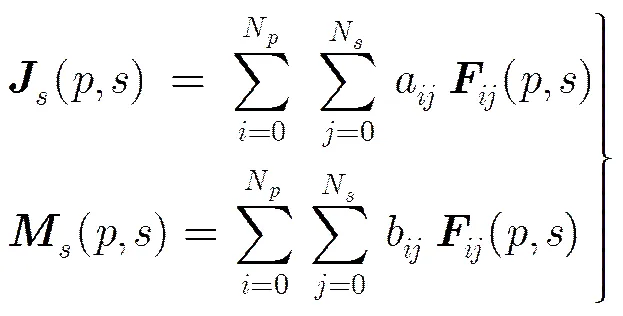
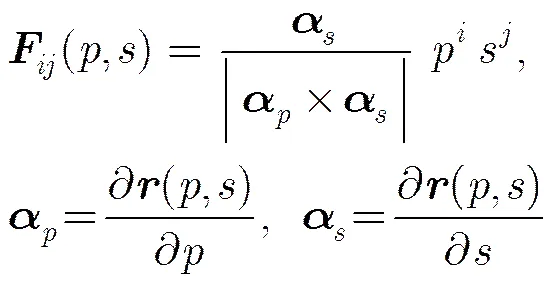
2.2 区域分解算法
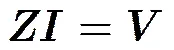
对于几何上不连续的电磁目标,我们可将其适当的分成若干个子区域,如图2所示,将目标划分为个子区域。由于各个子区域几何上互不相连,区域之间不存在电流的连续性问题,理论上有严格的数值解。只需将各个子区域分别采用高阶矩量法求出,然后考虑各区域间耦合作用,通过迭代就可以准确求出整个问题的解。
这里以两个区域为例,即=2,式(4)矩阵方程可写为
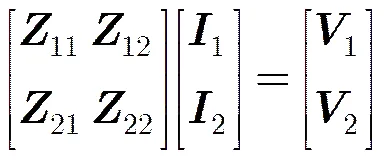
图2 区域分解示意图
采用高斯赛德尔迭代方法求解矩阵方程式(5),设置迭代收敛精度为,初始时,电流,则第次迭代时,区域的电流可表示为[15,16]
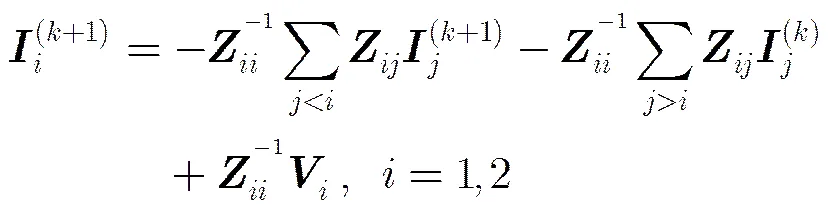
3 数值算例
这里以一个机载微带相控阵问题为例来表明本文方法的高效性,机载相控阵模型如图3(a)和图3(b)所示。阵列尺寸为7.54 m×1.57 m×0.02 m,单元数为26×6,工作频率为400 MHz。将该微带阵列架设到飞机平台上,飞机平台的尺寸为52.69 m×53.74 m×14.97 m,阵中心距离飞机机背顶部5.5 m,距离机头25.3 m。阵列主波束在方位面内分别向机翼两侧进行扫描-60°, -30°, 0°, 30°, 60°(主波束指向机翼为0°),如图3(c)所示。此处将该仿真模型分为两个区域进行求解,即微带阵列区域和机载平台区域。
图4–图6给出了阵列安装到飞机平台前后的2维和3维方向图。从图中可以看出,阵列安装到飞机平台后增益最大值较天线本身均有微小的增加,方向图主瓣出现很多毛刺,受飞机机翼的影响,阵列俯仰面副瓣电平明显降低。阵列主波束直指向机翼时,天线方向图受扰最为严重,其主波束变窄开裂并出现很多毛刺,图6(b)中在105°~180°范围内天线副瓣电平降低大约15 dB且发生剧烈抖动。随着阵列主波束偏离机翼,其受飞机平台的影响逐渐减小,阵列方向图变化减弱。
为验证本文区域分解法(DDM)的准确性,图5和图6中同时给出主波束直指向机翼时的整体矩量法解作对比。对比可见,两种方法的计算结果吻合良好。值得注意的是,在利用本文方法求解时,由于在整个相位扫描过程中飞机平台保持不变,此处只需要计算一次。当阵列相位变化时,仅需重新计算阵列所在区域,通过两个区域间的迭代就可以得到整体目标的解。表1给出了求解这一问题的计算资源和时间。由表1可见飞机平台的未知量为167219,在整个计算中占相当大的比例。虽然初次计算时,区域分解方法消耗的时间比矩量法整体求解时间略长,但在其余扫描角度的计算中优势极其明显,故利用本文方法无疑可以大幅度节省这一问题的计算时间,这在工程应用中具有很重要的意义。本算例使用的计算机平台为一集群系统共包含136个刀片节点,每个刀片节点配置两颗Intel Xeon E5-2692v2 2.2 GHz 12核的CPU, 64 GB内存,2块900 GB SAS硬盘,集群系统使用Mellanox FDR 56 Gb/s InfiniBand 进行互联。
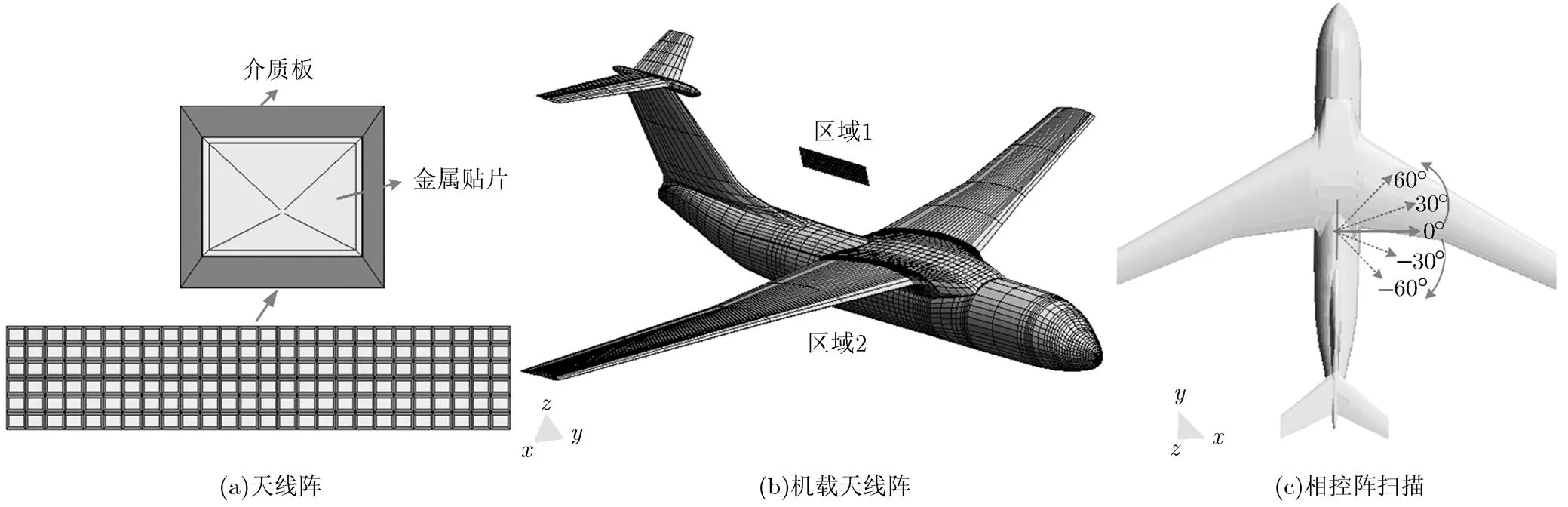
图3 26×6微带天线阵加载飞机平台仿真模型
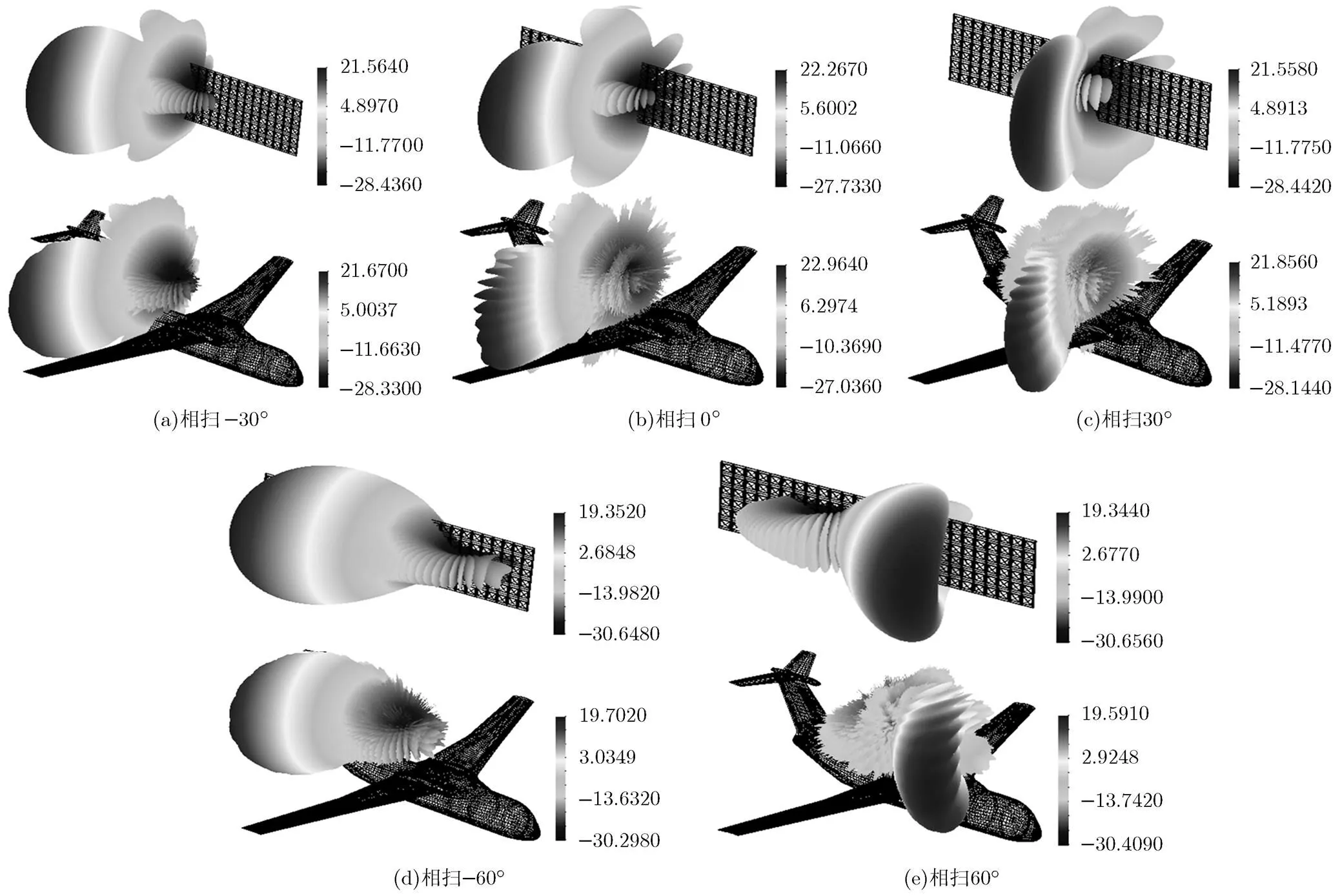
图4 3维增益方向图
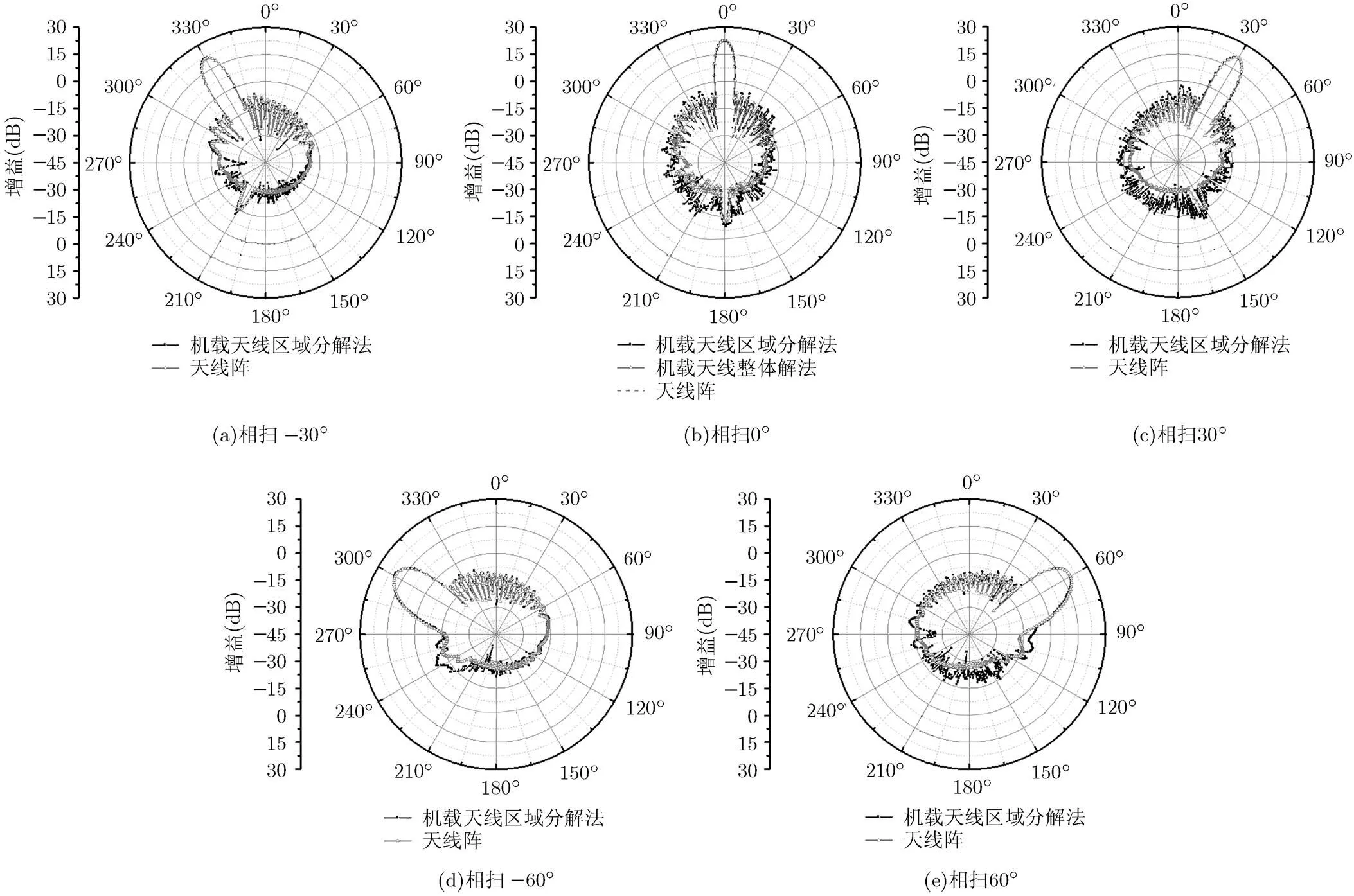
图5 机载雷达相控阵天线2维方位面增益方向图

图6 机载雷达相控阵天线2维俯仰面增益方向图
表1 计算数据

计算方法区域个数未知量个数CPU核数计算时间(s) 区域分解法2167219 (飞机平台)240扫描角178607557 扫描角2 420 扫描角3 434 37525 (天线阵)扫描角4 425 扫描角5 418 整体解法1225016240扫描角1697334865 扫描角26973 扫描角36973 扫描角46973 扫描角56973
4 结束语
基于并行核外高阶矩量法,本文利用区域分解法(DDM)对机载微带相控阵在相位扫描过程中的受扰电磁特性进行了仿真分析,并与矩量法整体求解法(DDM)的结果进行了对比。本文的研究目的是提出一种能够快速高效地解决机载相控阵天线布局问题的途径,该方法在充分利用相控阵雷达天线相位扫描或改变安装位置时,其机载平台区域保持不变的特点,将机载平台区域计算得到的阻抗矩阵等求解相关数据存储到本地磁盘中以供重复使用,大幅度降低了这一系统问题的计算量和计算时间。数值结果也表明了这一方案的高效性。接下来的工作中将会对该方法作进一步拓展研究,例如对平台进行分区域求解及多种电磁算法相结合等。使其能够高效分析更多的电磁问题。另外,目前主要关注的是载机平台处于静态时对雷达天线性能的影响,关于运动状态下的机载雷达天线性能分析以及气动与电磁联合仿真等问题正在研究中。
[1] 林中朝, 陈岩, 张玉, 等. 国产CPU平台中并行高阶矩量法研究[J]. 西安电子科技大学学报, 2015, 42(3): 43-47. doi: 10.3969/j.issn.1001-2400.2015.03.008.
LIN Zhongchao, CHEN Yan, ZHANG Yu,. Study of the parallel higher-order MoM on a domestically-made CPU platform[J]., 2015, 42(3): 43-47. doi: 10.3969/j.issn.1001-2400.2015.03.008.
[2] TOSELLI A and WIDLUND O. Domain Decomposition MethodsAlgorithms and Theory[M]. New York: Springer, 2005: 75-131.
[3] 朱汉清. 区域分解法在电磁问题分析中的应用研究[D]. [博士论文], 电子科技大学, 2002.
ZHU Hanqing. Application of domain decomposition method in the analysis of electromagnetic problems[D]. [Ph.D. dissertation], University of Electronic Science and Technology of China, 2002.
[4] RAO S M. A true domain decomposition procedure based on method of moments to handle electrically large bodies[J]., 2012, 60(9): 4233-4238. doi: 10.1109/TAP.2012.2207056.
[5] STEINBACH O and WINDIACH M. Stable boundary element domain decomposition methods for the Helmholtz equation[J]., 2011, 118(1): 171-195. doi: 10.1007/s00211-010-0315-6.
[6] 王少刚, 关鑫璞, 王党卫, 等. 求解电场积分方程的高阶矩量法[J]. 电子与信息学报, 2007, 29(9): 2265-2268.
WANG Shaogang, GUAN Xinpu, WANG Dangwei,. Solution of the electric field integral equation using higher-order method of moments[J].&, 2007, 29(9): 2265-2268.
[7] ZHANG Yu, LIN Zhongchao, ZHAO Xunwang,. Performance of a massively parallel higher-order method of moment code using thousands of CPUs and its applications[J]., 2014, 62(12): 6317-6324. doi: 10.1109/TAP.2014.2361135.
[8] ZHANG Yu and SARKAR T K. Parallel Solution of Integral Equation Based EM Problems in the Frequency Domain[M]. Hoboken NJ, Wiley-IEEE, 2009: 107-136. doi: 10.1002/ 9780470495094.
[9] 王长清. 现代计算电磁学基础[M]. 北京: 北京大学出版社, 2005: 116-157.
WANG Changqing. Computational Advanced Electro- magnetics[M]. Beijing: Pe king University Press, 2005: 116-157.
[10] 盛新庆. 计算电磁学要论[M]. 合肥: 中国科学技术大学出版社, 2008: 17-87.
SHENG Xinqing. A Brief Treatise on Computational Electromagnetics[M]. Hefei: Science and Technology of China Press, 2008: 17-87.
[11] LI M K and CHEW W C. Wave-field interaction with complex structures using equivalence principle algorithm[J]., 2007, 55(1): 130-138. doi: 10.1109/TAP.2006.888453.
[12] PENG Zhen, WANG Xiaochuan, and LEE J F. Integral equation based domain decomposition method for solving electromagnetic wave scattering from non-penetrable objects[J]., 2011, 59(9): 3328-3338. doi: 10.1109/TAP.2011.216542.
[13] MAURIN J, BARKA A, GOBIN V,. Domain decomposition method using integral equations and adaptive cross approximation IE-ACA-DDM for studying antenna radiation and wave scattering from large metallic platforms[J]., 2015, 63(12): 5698-5708. doi: 10.1109/TAP.2015.2481931.
[14] BARKA A. Integration of antennas onboard vehicles and diffraction by large and complex structures with multiple- domain-multiple-methods techniques[J]., 2013, 101(2): 280-297. doi: 10.1109/JPROC.2012. 2199069.
[15] BAUTISTA M, VIPIANA F, FRANCAVILLA M,. A nonconformal domain decomposition scheme for the analysis of multi-scale structures[J]., 2015, 63(8): 3548-3560. doi: 10.1109/TAP. 2015.2430873.
[16] WIEDENMANN O and EIBERT T. A domain decomposition method for boundary integral equations using transmission condition based on the near-zone couplings[J]., 2014, 62(8): 4105-4114. doi: 10.1109/TAP.2014.2322881.
Analysis of Disturbed Large Airborne Phased Radar Antenna Array
LI Yanyan LIN Zhongchao ZHANG Yu ZHAO Xunwang LU Hongmin
(,,710071,)
A parallel higher-order and out-of-core based Domain Decomposition Method (DDM) is proposed for analyzing the disturbed characteristics of large airborne phased radar antenna array. When the phase of main beam sweeps for the airborne phased radar antenna array, the problem is divided into two parts: radar antenna array and airborne platform. The platform which remains unchanged during the overall solution is simulated only once at the beginning, and then the relative data, such as impedance matrixes are written into hard disk using out-of-core technique. When the phase sweeps, only the phased antenna array part is concerned. Finally, the accurate results are obtained by iterative solution. This method largely reduces the CPU time and storage requirements. The numerical example demonstrates that the proposed method is very suitable for analyzing the layout of large airborne phased radar antenna array.
Phased radar; Domain Decomposition Method (DDM); Higher-order MoM
TN958.92; TN957.2
A
1009-5896(2017)03-0684-06
10.11999/JEIT160425
2016-04-28;改回日期:2016-09-02;
2016-11-14
张玉 yuseexidian@163.com
国家自然科学基金(61301069),教育部新世纪优秀人才支持计划(NCET-13-0949),中央高校基本科研业务费(JB160218),国家863计划(2012AA01A308)
The National Natural Science Foundation of China (61301069), The Program for New Century Excellent Talents in University of China (NCET-13-0949), The Fundamental Research Funds for the Central Universities (JB160218), The National 863 Program of China (2012AA01A308)
李艳艳: 女,1988年生,博士,研究方向为计算电磁学、大型机载天线阵列分析.
林中朝: 男,1988年生,博士,研究方向为计算电磁学、大规模并行算法.
张 玉: 男,1978年生,教授,研究方向为计算电磁学、大规模并行算法.
赵勋旺: 男,1983年生,副教授,研究方向为计算电磁学、大规模并行算法.
路宏敏: 男,1961年生,教授,研究方向为电磁兼容、微波技术与天线、信号完整性分析.

