基于星座软信息的猝发信号盲均衡算法
黄 焱 邱钊洋 欧阳喜
基于星座软信息的猝发信号盲均衡算法
黄 焱 邱钊洋*欧阳喜
(解放军信息工程大学信息系统工程学院 郑州 450001)
针对非协作通信中猝发类幅相调制信号先验信息少,数据量小,信噪比低等特点,该文在修正常模算法(MCMA)数据重用算法基础之上提出一种基于星座软信息的猝发信号盲均衡算法,采用接收信号的统计信息代替调制信息,并引入循环迭代的思想,实现了猝发信号的快速盲均衡。此方案不需要调制方式等先验信息,复杂度低,灵活性好,适合非合作接收条件。仿真表明,在抗噪声,抗频偏,抗相偏性能与传统算法基本保持一致的前提下,该文算法在收敛速度,稳态误差等方面均优于原算法,对深衰落信道效果显著,可应用于工程实践。
非合作接收;猝发信号;盲均衡;循环迭代
1 引言
多径效应引起的码间串扰是影响通信可靠性的重要因素之一,通过均衡技术减弱码间串扰是实现解调端星座图恢复的有效方法,其中盲均衡是指接收端不使用训练序列对传输信道进行盲估计和抵消,可以有效节省频带资源,且能够自适应信道和信号的各种变化,是均衡技术研究的热点和难点。在日益复杂的电磁环境中,大量出现着猝发类幅相调制信号,非合作接收条件下,第三方没有这类信号调制类型的先验知识,同时很难获取训练序列,尤其是在诸如载波监视、监测、通信侦察和其它非协作通信中,所以此情形下盲均衡问题一直是一个十分重要的课题。现有的盲均衡算法虽然不需要训练序列的辅助,但要求已知信号的调制方式及调制阶数,算法根据信号的标准星座点分布设计[1],这大大限制了其在非合作通信中的应用。由此调制识别成为盲均衡前的必要环节,调制识别技术研究多年,存在多径效应的情况下,这些算法普遍存在复杂度高,准确率低,且要求数据量足够多,信噪比足够高等,不能有效地应对日益复杂的电磁环境,故不能为均衡提供可靠的调制信息。现实中迫切需要一种灵活快速的盲均衡算法以应对无调制信息下猝发信号的均衡问题。
修正常模算法(MCMA)由文献[5]提出,这种方法可以应对各种幅相调制类信号,其复杂度低,灵活性好,后来被许多学者改进,并被应用于实际的通信系统中。MCMA算法结合数据重用思想是目前针对已知调制类猝发信号盲均衡的一种有效手段,许华等人在文献[6]中详细分析了常模算法结合数据重用思想在盲均衡中的性能和约束条件,使该算法更贴近实用。
2 幅相调制类信号的盲解调流程及MCMA数据重用算法
经统计,卫星通信中90%以上采用幅相调制类信号,包括MPSK, MAPSK, MQAM等。此外,短波通信、移动通信中也广泛存在着幅相调制类信号。非合作接收条件下幅相调制类通信信号的解调一般需要依次完成调制识别、定时同步、载波同步,均衡等一系列工作。
对于幅相调制信号的盲解调技术研究已进行多年,其定时同步,载波同步等均已有较为成熟的方法,如平方定时法[7],M次方谱法[8]等,这些方法都是适合于非合作接收条件的经典算法。盲均衡也是盲解调中的关键一环,MCMA算法广泛的适用性和操作的简易性使其一经提出便引起了巨大关注。目前针对非合作通信中猝发信号,应用最广泛的基于数据重用思想的盲均衡流程如图1所示。

图1 现有MCMA数据重用均衡系统原理框图
其中MCMA算法采用发送符号的统计信息设计调整准则[5]。其代价函数为

其中,
(2)
对代价函数求导采用LMS(最小均方误差)准则下的瞬时梯度法可得到均衡滤波器的调整准则为

当前研究中数据重用的方式主要分为4种:单数据向量的重用[9],数据向量串的重用[10],改进的数据向量串的重用[11],数据向量串的循环重用[12]。文献[11]提出的改进的数据向量串重用算法,在收敛速度和稳态误差方面均较优,同时证明了令尽可能长的整块的接收数据循环输入至均衡器时,均衡效果最理想。本文提出算法将以其作为比较对象。
非合作接收条件下,原MCMA算法应用于猝发信号时存在显而易见的矛盾,即调制识别的精度受多径程度的影响,而多径程度的减弱又要求高精度的调制识别。这大大限制了其在猝发类非协作通信信号盲均衡中的应用。本文针对此问题,对MCMA数据重用算法的运行流程进行改进,以克服非合作接收条件下猝发信号无调制信息,数据量小,有频偏等一系列不利因素,增加其适用性,灵活性和收敛速度,同时也为后期进行调制识别,载波同步提供有力辅助。
3 算法设计
3.1 MCMA算法统计量替换与循环迭代思想的引入
通过对MCMA算法的设计流程的研究可以发现,其对调制方式信息的使用集中体现在式(2),式(2)的意义是提取发送符号的统计信息,发送符号未知,根据发送符号的随机性,可通过其调制方式对应的标准星座进行计算。通过将式(2)变换为式(4),即将先验的调制信息替换为现有的接收信号的统计信息,可消除对调制方式的依赖,实现非合作接收下的全盲均衡。改进算法,的表达式为

图2 循环迭代盲均衡系统原理框图
算法步骤如下:

步骤4 检测均衡器的收敛性,若是则结束,均衡器的输出序列即为均衡结果;若为否,转步骤5;
步骤6 将均衡器与输入符号序列进行线性卷积,卷积结果作为均衡器第次的输入序列,转步骤3 。
步骤6保证了循环迭代过程的串联效应,卷积的可分解性使均衡过程不至引起噪声放大导致的不收敛问题,更充分地利用了均衡器输出的中间结果。此种结构的实质是多级自适应均衡器串联,逐级叠加地修正多径效应带来的码间串扰。并联结构的均衡器在收敛速度上的缺陷是明显的,基于循环迭代思想的均衡器因其实质上的串联结构,理论上可以明显提高收敛速度。
3.2 算法性能分析
3.2.1 收敛性能 从基础CMA算法模型出发,其均衡器更新准则为

(7)
Godard在文献[13]中指出,当保持均衡器输入信号不变,将增大至时,均衡器的稳态解将收敛于,其中表示原始的稳态解,说明均衡器系数会发生线性变化,此时用剩余ISI来衡量稳态误差时,的变化将不影响剩余ISI的大小,影响的是均衡器输出信号的功率,此影响可以在信号均衡完成后对信号进行能量归一化来消除。下面讨论的变化对算法收敛速度的影响。为简化分析,忽略均衡器初始化对算法的影响。此处不失一般性,令。由(6)式得,均衡器每次的调整量为

稳态误差相同时,有
(9)
此时,

(11)

联立式(11),式(12),得
(13)
多径效应及噪声对星座产生的影响可以用图3说明。

图3 多径效应对信号模值分布的影响
多径信道在不影响星座整体功率的情况下将各模值离散化,从而使星座图被扰乱而无法用于判决,这种扰乱增加了星座图模值的方差,且由于星座图的对称性,等效地增加了星座图实虚部的方差。改进算法采用类似式(13)计算的统计量(只是将实虚部分开),相当于经过多径信道引起模值方差的增大,从而增大了统计量,此时均衡器的稳态解线性增大,可实现剩余ISI不变的同时加快收敛速度。
3.2.2 频偏下均衡器的收敛特性 在非合作接收条件下,由于调制方式未知且含有多径信道影响,往往载波估计精度有限,所以均衡算法必须考虑到频差,即对载波频偏具有鲁棒性。由于本文算法采用了接收信号的统计信息代替发送符号的统计信息,所以需要研究频差对统计量的影响。令

于是,
(15)
化简得
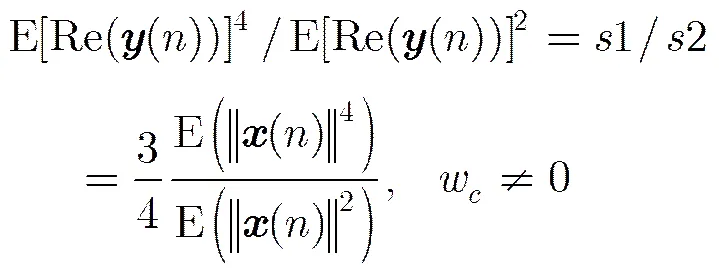
(17)
式(17)表明,存在频偏情况下,信号的实部虚部均衡器统计量是相等的,故本文算法在存在频偏的前提下仅适用于实虚对称星座(所有的PSK类,正方形QAM,所有的APSK类等等),而对非对称星座(如方形8QAM, 32QAM)的含频偏下盲均衡,则不适用;无频偏时,本文算法适合所有幅相调制信号的盲均衡。一般情况下,含频偏信号的均衡要求对接收星座先进行频偏估计,去频偏后再进行均衡,这是根据信号畸变的顺序确定,而本文经过推导证明,去频偏可以在均衡之后进行,只是需要均衡的信道发生了变化。
含频偏信号可建模为
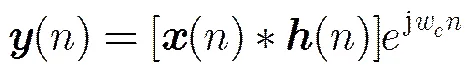
(19)
(20)
式(20)的意义是,多径信道下对信号加频偏,相当于含频偏信号经过了另一个多径信道,只是信道抽头系数与原信道相比发生了变化。由此可以先进行盲均衡再去频偏,这是算法抗频偏的理论基础。
3.2.3 相偏下均衡器的收敛特性 随机的载波初相及复多径信道等带来的相偏对统计信息的影响不容忽略。用表示含相偏信号。

(22)
对虚部统计量计算亦有相似结果。可见相偏引起的旋转对实虚部的影响是对称的,对于实虚对称的方形星座而言,含相偏信号的实虚部统计量继续保持一致且略大于原统计量。这说明相偏不会对算法收敛产生影响。随着均衡器对数据的均衡,信道的影响逐渐变弱,对统计信息的影响将随之逐渐削弱,同时由于MCMA算法的纠相偏性能,可使载波初相带来的影响同步地得到消除。
3.3 均衡器收敛性检测
由于针对不同的信道环境,均衡器循环迭代的次数不可预估,故需对均衡器的循环迭代设置终止条件。通过对图2提出的基于循环迭代结构的均衡器结构的分析可以得出,均衡器的输入是上一次的输出,故当均衡器收敛时,理论上输入与输出应保持相同,此时抽头系数应恢复为=[0 00 0 0 1 0 0 00 0]。而实际应用中,均衡器输入输出不可能完全相同,故此时可用滤波器系数与的偏差—抽头系数剩余均方误差()来衡量第次输入与输出之间的差异程度。

3.4 改进的非合作猝发类幅相调制信号盲解调流程
改进的非合作猝发类幅相调制信号盲解调流程如图4所示。本文均衡算法可将多径信道下信号的调制识别问题大大简化,从而实现准确度高,简单易操作的幅相调制信号盲解调流程。首先对接收到的过采信号进行定时同步,可采用平方定时算法,粗估载频进行下变频,获得含频偏星座图,然后采用本文盲均衡算法,均衡多径效应,最后进行频偏估计与消除、相偏估计与消除,判决获得比特流。本文算法的本质是盲均衡模块的前移,这种结构设计,可在信号处理初期减弱多径效应带来的干扰,以改善载波同步、调制识别模块的输入端信号质量,从而提升其精度。实际中,当多径已得到消除时,调制识别和频偏估计等将成为相对简单的问题[14],目前已有相对成熟的抗频偏调制识别算法,载波频偏也可以经过后续的估计算法进行补偿,如锁相环路、M次方谱等前向及后向估计算法[15]等。

图4 改进的非合作猝发类幅相调制信号盲解调流程
4 仿真实验
4.1 性能评估指标量计算
均衡器的均衡效果一般用剩余码间干扰作为衡量准则,对于MCMA数据重用算法,剩余ISI定义为

而对于本文算法剩余ISI计算中等效信道可通过式(25)计算:
(25)
4.2 蒙特卡罗仿真
实验平台选择MATLAB2014a,下文就收敛性能、抗噪性能、抗频偏与相偏性能分别进行蒙特卡罗仿真,对比本文算法与原MCMA算法性能。
4.2.1 多径信道下收敛性能 为了测试算法的抗多径性能,本实验选取了两组衰落程度不同的多径信道,如图5所示,信道2的衰落程度明显高于信道1。多径信道的码间干扰程度与其频域的衰落性成正相关,码间干扰越严重,频域衰落越严重,同时对接收端均衡算法的要求就越高。故本实验采用这两个信道对两种算法抗多径性能进行测试。

图5 信道1和信道2频域衰落程度对比
图6、图7、图8表明,在信道衰落程度较轻的信道1,两种算法性能差距不大,收敛速度均随步长因子增大而加快,稳态误差对步长因子具有鲁棒性,相等的步长因子下本文算法仅在速度上略优于MCMA数据重用算法,稳态误差二者基本相同。而在码间干扰严重的信道2,本文算法在收敛速度快的同时稳态误差更小,有约7 dB均衡增益,同时收敛速度对步长因子具有一定的鲁棒性,这点在实际应用中也是十分重要的。在深衰落信道环境下,MCMA算法性能很难提升,这是算法本身固有的缺陷。本文算法由于采用了循环迭代的均衡结构,获得了更好的抗多径性能,在对抗深衰落信道时优势明显。
4.2.2 均衡器收敛性能随信噪比变化 为了测试本文算法的抗噪性能,选取了码间干扰稍弱信道,并通过实验测试,信噪比无穷大时,两种算法的最终的收敛性能相同,通过不断增加噪声功率,测试两种算法的收敛性能。

图6 信道1均衡结果
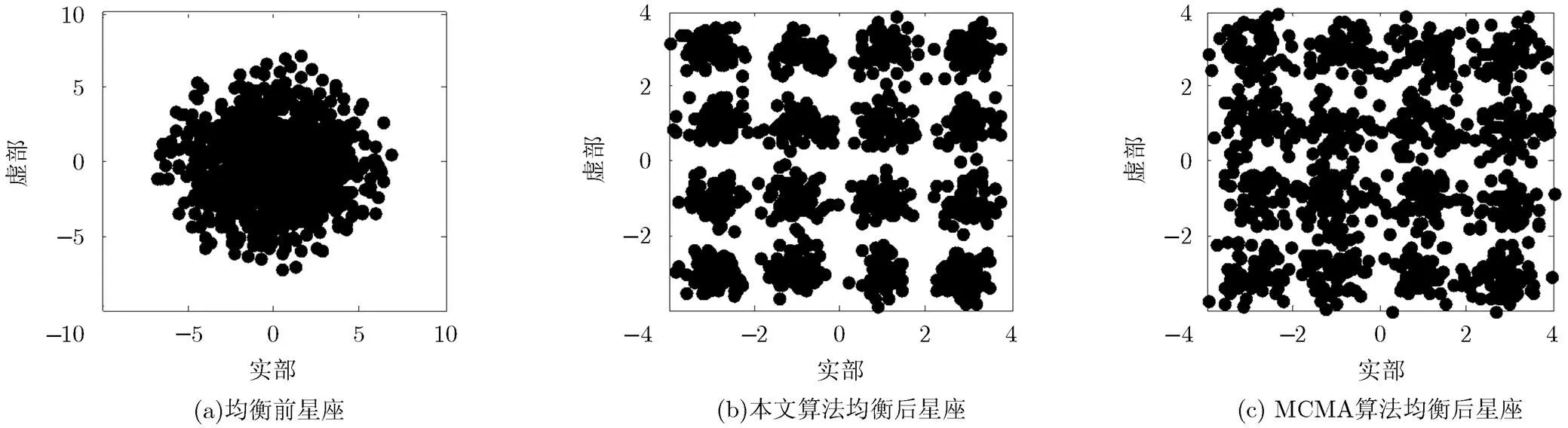
图7 信道2均衡结果

图8 收敛性能对比
由图9可见,本文算法在不使用调制信息的优势基础上,抗噪性能并无损失,基本与原MCMA数据重用算法保持一致。
4.2.3 均衡器收敛均方误差随频偏及相偏的变化
由图10(a)可以看出,两种算法性能稳态误差均与频偏有关。由于实验信号为16QAM调制,是旋转对称星座,故归一化频偏为0,1/4,1/2时,算法相当于无频偏即调制层相位模糊。这些值之间,算法性能有约8 dB的退化,本文算法略优于MCMA数据重用算法。由图10(b)可以看出,两种算法性能稳态误差均不受相偏的影响,保持了纠全范围相偏的能力。
5 结束语
本文针对非合作接收条件特点,通过改进经典的MCMA均衡结构,基于接收端星座软信息实现了无调制信息,含频偏、短数据量下的猝发信号循环迭代盲均衡器结构设计,在需要先验信息少的基础上,相比目前常用的MCMA数据重用算法,可以获得更快收敛速度的同时得到更佳的均衡效果,同时保持了原算法的抗噪性能、纠相偏性能。最后通过实验证明了算法的有效性和实用性,该算法的研究实现对后期的调制识别及盲解调等具有重要意义。

图9 抗噪性能对比

图10 两种算法抗频偏和相偏能力对比
[1] ABRAR Shafayat and NANDI Asoke K. An adaptive constant modulus blind equalization algorithm and its stochastic stability analysis[J]., 2010, 17(1): 55-58.doi: 10.1109/LSP.2009. 2031765.
[2] 杨发权. 无线通信信号调制识别关键技术与理论研究[D]. [博士论文], 西安电子科技大学, 2015.
YANG Faquan. The key techniques and theories research on Modulation recognition for wireless communication signals [D]. [Ph.D. dissertation], Xidian university, 2015.
[3] 赵雄文, 郭春霞, 李景春. 基于高阶累积量和循环谱的信号调制方式混合识别算法[J]. 电子与信息学报, 2016, 38(3): 674-680. doi: 10.11999/JEIT150747.
ZHAO Xiongwen, GUO Chunxia, and LI Jingchun. Mixed recognition algorithm for signal modulation schemes by high-order cumulants and cyclic spectrum[J].&, 2016, 38(3): 674-680. doi: 10.11999/JEIT150747.
[4] 陈泽艺. 基于循环谱和高阶累积量的联合模式识别方法[J].电讯技术, 2015, 16(3): 328-332. doi: 10.3969/j.issn.1001-893x. 2015.03.017.
CHEN Zeyi. A combined modulation recognition based on cyclic spectrum and high-order cumulants[J]., 2015, 16(3): 328-332. doi: 10.3969/j.issn.1001-893x.2015.03.017.
[5] KIL Yamoh and YONG Ohkchin. Modified constant modulus algorithm: blind equalization and carrier phase recovery algorithm[C]. IEEE International Conference on Communications, Seattle, USA, 1995: 498-502. doi: 10.1109 /ICC.1995.525219.
[6] 许华, 郑辉, 张冬梅. 基于“数据重用”的常模盲均衡算法[J].通信学报, 2009, 30(7): 73-77.
XU Hua, ZHENG Hui, and ZHANG Dongmei. Analysis of constant modulus blind equalization algorithms based on “data reuse”[J]., 2009, 30(7): 73-77.
[7] OERDER M and MEYR H. Digital filter and square timing recovery[J]., 1988, 36(5): 605-612. doi: 10.1109/26.1476.
[8] 刘少林. MPSK信号调制方式识别与参数估计[D]. [博士论文],北京邮电大学, 2015.
LIU Shaolin. Modulation recognition and parameter estimation of MPSK signals[D]. [Ph.D. dissertation], Beijing University of Posts and Telecommunications, 2015.
[9] ROY S and SHYNK J. Analysis of the data-reusing LMS algorithm[C]. The Thirty-Second Midwest Symposium on Circuits and Systems, Champaign, IL, USA, 1989: 1127-1130. doi: 10.1109/MWSCAS.1989.102053.
[10] SCHNAUFER B A and JENKINS W K. New data-reusing LMS algorithms for improved convergence[C]. The Twenty- Seventh Asilomar Conference on Signals, Systems and Computers, California, USA, 1993: 1584-1588. doi: 10.1109/ ACSSC.1993.342346.
[11] SONI R, GALLIVAN K, and JENKINS W. Low-complexity data reusing methods in adaptive filtering[J]., 2004, 52(2): 394-405. doi: 10.1109/TSP.2003.821338.
[12] 许华. 短时突发信号的盲处理技术研究[D]. [博士论文], 解放军信息工程大学, 2005.
XU Hua. Blind equalization techniques on short burst signals [D]. [Ph.D. dissertation], Information Engineering University of PLA, 2005.
[13] GODARD D N. Self-recovering equalization and carrier tracking in two-dimensional data communication systems[J]., 1980, 28(11): 1867-1875. doi: 10.1109/TCOM.1980.1094608.
[14] 廖灿辉, 涂世龙, 万坚. 一种抗频偏的卫星幅相调制信号识别算法[J]. 电子与信息学报, 2014, 36(2): 346-352. doi: 10.3724/ SP.J.1146.2013.00512.
LIAO Canhui, TU Shilong and WAN Jian. An anti- frequency-offset algorithm for modulation recognition of satellite amplitude-phase modulated signal[J].&, 2014, 36(2): 346-352. doi: 10.3724/SP.J.1146.2013.00512.
[15] 赵颖. 基于改进算法的调制信号的载波频率估计[J]. 电子设计工程, 2016, 24(6): 29-31. doi: 10.14022/j.cnki.dzsjgc.2016. 06.065.
ZHAO Ying. Estimation of carrier frequency of modulation signal based on improved algorithm[J]., 2016, 24(6): 29-31. doi: 10.14022/j.cnki.dzsjgc. 2016.06.065.
Blind Equalization for Burst Signals Based on Soft Information of Constellation
HUANG Yan QIU Zhaoyang OUYANG Xi
(,,, 450001,)
For the characteristics of amplitude and phase-modulated signals in non-cooperative burst communication like less known information, less data, and low signal to noise ratio, Modified Constant Modulus Algorithm (MCMA) is concentrated on and a blind equalization algorithm is designed based on soft constellation information. The proposed algorithm could achieve a quick blind equalization while just using the statistics of the samples of the receiver and adopting the ideology of cyclic iteration. The scheme has a lower complexity, better flexibility while disregarding the modulation type, which made it a good choice for non-cooperative condition. The simulation indicates that the new algorithm has a superior on existing algorithms in converging speed, equalization result, and durability while keeping the performance on defensing noise, frequency offset and phase offset, and can be applied into engineering practice.
Non-cooperative reception; Burst signals; Blind equalization; Cyclic iteration
TN911.6
A
1009-5896(2017)03-0568-07
10.11999/JEIT160420
2016-04-28;改回日期:2016-09-23;
2016-11-14
邱钊洋 qiuzhaoyang2010100@163.com
国家自然科学基金(61072046)
The National Natural Science Foundation of China (61072046)
黄 焱: 男,1964年生,教授,研究方向为通信信号分析与处理.
邱钊洋: 男,1991年生,硕士生,研究方向为通信信号分析与软件无线电.
欧阳喜: 男,1973年生,副教授,研究方向为通信信号分析与软件无线电.

