利用三分量磁传感器解算姿态问题研究
边宇舰 焦君圣
(声纳技术重点实验室 第七一五研究所,杭州,310023)
利用三分量磁传感器解算姿态问题研究
边宇舰 焦君圣
(声纳技术重点实验室 第七一五研究所,杭州,310023)
为精准测量载体姿态,在利用磁传感器测量地磁场来计算载体航向的基础上,从原理上推导如何利用Terrella6磁传感器来测量载体姿态角。通过数据比对,误差<1°,验证了文章推导出的姿态角解算公式正确。
三分量;磁传感器;姿态;欧拉角;坐标旋转
了解载体姿态对于载体导航、定位等工作具有重大帮助[1]。载体姿态的测量方式有多种,根据对象以及任务要求的不同,姿态传感器可选用磁感应式、惯性式等。磁感应传感器由于利用了地磁场,结构中没有可动部件,所以具有较好的抗冲击和抗干扰性,而且其结构简单、重量轻、体积较小、启动快、成本低,成为许多载体姿态测量的首选器件[2]。三分量磁传感器由三轴微加速度计和三轴微磁强计组成,利用大地磁场和重力场在地理坐标系和载体坐标系之间的方向余弦转换进行绝对角度解算,克服了传统的(如陀螺测量)需要积分得到姿态角,避免了累积误差,保证了长期的测角精度[3]。
1 姿态测量原理
目前,已有文献对姿态角的定义都不尽相同:有的定义俯仰角为载体纵轴与纵向水平轴之间的夹角;有的甚至直接定义姿态角等于欧拉角。看似类似,实则却有偏差并且是片面的。因没有姿态角的权威定义,学者参考时常会混淆[4]。在计算姿态角时,方法更是层出不穷[5]。使用欧拉角解算姿态角时,对于夹角的顺序和标记、夹角的两个轴的指定,没有任何标准规定[6],科学家对此也未达成共识。而在实际中用到欧拉角时,必须明确的表示出夹角的顺序,指定其参考轴。实际上,有许多方法可以设定两个坐标系的相对取向,欧拉角方法只是其中的一种[7]。此外,不同的作者会用不同组合的欧拉角来描述,或用不同的名字表示欧拉角。因此,使用欧拉角前,必须先做好明确的定义。
姿态测量系统需要给出的载体姿态信息是载体相对于地平面的三个姿态角:俯仰角、横滚角、航向角,这实际上是载体坐标系与地理坐标系三轴间的夹角,具体定义如下:
(1)俯仰角:载体纵轴和水平面之间的夹角,向上为正,向下为负,定义域为−90°~90°。
(2)横滚角:载体纵向对称面与纵向铅垂平面之间的夹角。横滚角从铅垂平面算起,右倾为正,左倾为负,定义域为−180°~180°。
(3)航向角:载体纵轴在水平面上的投影与地理子午线之间的夹角。航向角的数值以地理北向为起点沿逆时针方向计算,定义域为0~360°[8]。
对于载体姿态的解算方法,比较常用的是余弦法、矩阵法和角度给定法。角度给定法具有简单易懂、便于理解的特点。角度给定法可以分为 RPY(Roll,Pitch,Yaw)和欧拉角方位表示法两种[9]。RPY法起源于描绘船舶的姿态,一个是绕船前进的方向即x轴方向的Roll转角,第二个是绕水平Y轴方向的Pitch角,第三个是绕铅垂z方向的Yaw角。RPY法中的x、y、z三轴是原坐标系的三轴,如图1所示。

图1 RPY角姿态描述方法
欧拉角计算载体姿态有很长的历史了,该方法不仅计算方便有效,最主要的是用它表示载体的姿态十分简洁明了[10]。欧拉角表示法与 RPY法是不同的,首先是绕着O-xyz的z轴旋转一个角度γ,得到新的坐标系O-x1y1z1;之后绕着新坐标系O-x1y1z1的xl轴旋转φ角,得到新的坐标系O-x2y2z2;再绕着O-x2y2z2的y2轴旋转θ角,得到最终的坐标系O-NED。每次的旋转就相当于进行一次坐标变换,这个过程可以用对应的变换矩阵来表示。各矩阵排列顺序是旋转顺序的逆序,这样可以确保在后面与坐标矩阵相乘时,首先旋转的角度矩阵能先与坐标矩阵相乘。
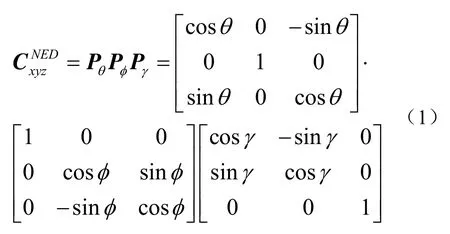
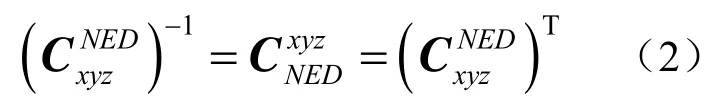
即坐标也是可以逆变换的[12],则有
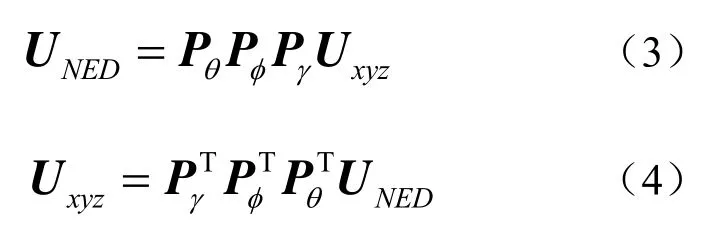
此处坐标系旋转变换时建议代入普通坐标系点进行验算。
欧拉角是坐标轴旋转时两个对应坐标轴之间的夹角,而俯仰角是载体纵轴和水平面之间的夹角,所以当且仅当先绕y产生俯仰角,再绕x产生横滚角时,姿态角与欧拉角相等。当先存在横滚角,再产生俯仰角时,姿态角与欧拉角不再相等。例如,当先绕y轴旋转30°,即存在俯仰角30°的情况下,再绕x轴旋转30°,即产生横滚角30°。此时载体的姿态与先产生30°横滚角,再产生30°俯仰角时的姿态是不相同的。因为欧拉角与 RPY法不同,每次坐标轴旋转都是绕上一次旋转完后新的坐标系轴进行的,因此旋转顺序很重要,须定义清楚。
2 利用加速度计算俯仰和横滚角
本文中定义的参考坐标系O-XHYHZH和传感器坐标系O-XYZ均是笛卡儿坐标系。默认参考坐标系为XH轴指向地球北极,YH轴与纬线平行指向东,ZH轴垂直水平面向下。传感器坐标系是传感器自身所在的坐标系。Terrella6传感器是通过感测地球地磁场和重力场所获得的信息来确定方位的。测量过程分为两步:首先由测得的重力加速度在传感器坐标系三个轴上的分量通过坐标旋转矩阵来确定其欧拉角;然后通过欧拉角将由磁传感器测得的传感器坐标下的三轴磁分量投影到参考坐标系,得到参考坐标系下的三轴磁分量,由该参数可以计算得到方位角。在传感器坐标系X、Y、Z轴上可分别测得重力加速度g在其上的分量Ax、Ay、Az,三者与重力加速度g存在一定的旋转对应关系。根据不同的旋转顺序,求出的欧拉角是不同的,由于投影三轴磁分量到参考坐标系只需用到欧拉角φ和θ,所以只解两个旋转矩阵即可。如果先绕X轴转再绕Y轴转,则根据旋转关系有

由此可得俯仰角和横滚角分别为

如果先绕Y轴转再绕X轴转,则旋转变换关系变为
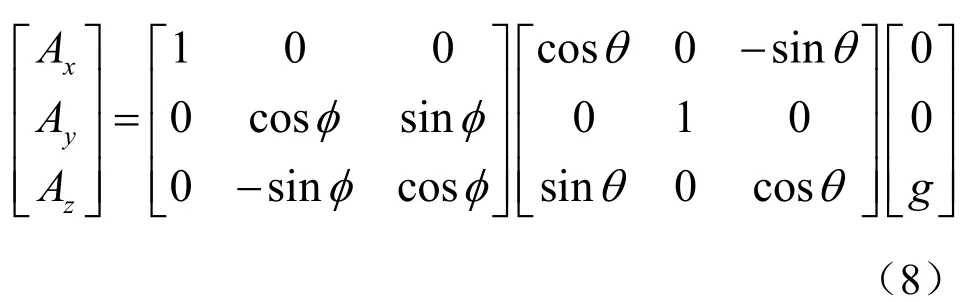
由此可得俯仰角和横滚角分别为

两种结果相似。根据上文的分析,只有先绕y轴旋转再绕x轴旋转时欧拉角才会与姿态角相等。因此只有第二种情况才是正确的。
3 利用磁场计算航向角
当传感器处在水平面上时,俯仰角α和横滚角β均为零,如图2所示。

图2 X-Y-Z坐标系内方位角定义
方位传感器方位角数学模型为:

式中,X、Y是磁传感器探测到地磁场H在两个互相垂直方向的分量。γ*角为传感器坐标系X轴正向与磁场水平分量之间的夹角,即X轴正向与磁北之间的夹角。γ*角减去或加上当地的磁偏角ε即得X轴正向与正北之间的夹角,即方位角(航向角)。
当传感器不平行水平面时,传感器坐标系O-XYZ与坐标系O-XHYHZH之间的关系用欧拉角和表示,其数学模型为:

则:

式中,X、Y和Z是三维磁传感器探测得到地磁场H在传感器三个互相垂直方向上的分量。YH和XH为利用欧拉角将测得的三轴磁分量投影到参考坐标系下的磁分量。根据式(9)、(10)、(15),我们就可以利用测量得到的数进行载体的三维姿态估计。
4 实验验证
Terrella6三分量磁传感器能够输出航向、俯仰、横滚角度值以及加速度和磁场强度分别在三轴上的分量。利用磁传感器输出的加速度和磁场分量计算其航向、俯仰和横滚,并与其自身测量所得姿态角度进行对比,以此来验证姿态角计算公式的正确性。通过串口将磁传感器的测量结果发送到上位机,调整传感器的姿态,使其输出不同结果,便于后期对比,测量结果如表1所示。表1中Mx、My、Mz分别表示载体坐标x、y、z轴上的地磁场分量。
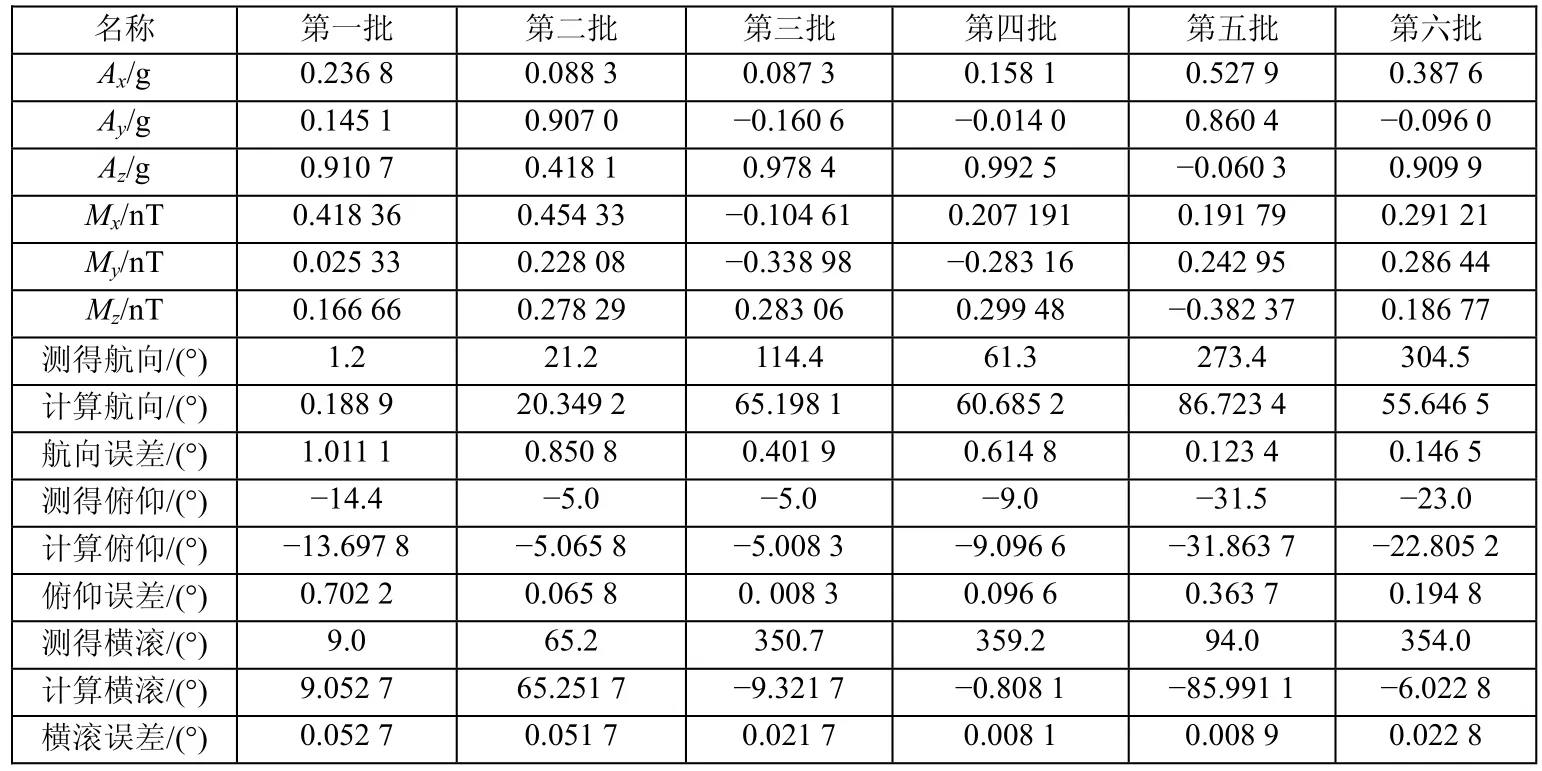
表1 用磁传感器实测数据与姿态解算公式计算姿态数据对比
通过实测数据,利用推导的姿态解算公式计算结果和传感器实测结果进行比较,航向、横滚、俯仰的计算误差都比较小,最大在1°误差左右,在可接受范围内,证明了推导出的姿态解算公式的正确性。表中有些航向角数据计算出来需要用 360°或180°相减才能得到传感器直接输出的数据,因为传感器内部已经处理过数据。
5 结论
在正确得到姿态解算公式之后,通过分析解算公式就能方便地进行误差分析,较为容易地得知影响姿态角的因素具体有哪些,对其精度影响有多大,从而进一步提高测量精度。
[1]岳志杰,王婷.AUV水下对接的导航和定位系统设计[C].2016 IEEE/OES China Ocean Acoustics Symposium,2016.
[2] LIU SHENG WU,ZHUANG JI DONG,HUNG J C,et al.Compass deviation analysis and compensation for a three-axis strapdown magnetic heading system[C].IFAC Symposia Series-Proceedings of a Triennial World Congress,1990.
[3]朱荣,周兆英.基于MEMS的姿态测量系统[J].测控技术,2002,(10):6-8.
[4]臧爱云,原魁,严志刚,等.磁传感器在导航系统中的应用[J].高技术通讯,2004,(10):53-57.
[5]高锋.应用磁阻传感器的数字航向仪设计[D].南京理工大学,2004.
[6]刘敬彪,郑玉冰,章雪挺.三轴磁罗盘的设计与误差校正[J].自动化仪表,2008,(9):10-12.
[7]刘武发,蒋秦,龚振邦.基于磁阻和MEMS加速度传感器的电子罗盘设计及应用[J].兵工学报,2008,(2):244-248.
[8]崔璐璐.基于 MEMS器件的姿态测量系统研究与实现[D].大连理工大学,2009.
[9]LIN Y,ZHANG W J,KOUBEK R J.On integration of interface design methods:can debates be resolved[J].Interacting with Computers,2006,18(4):709-722.
[10]张振友,李明,田应仲.物体空间姿态的实施测量方法研究[J].机械设计与研究,2008,(5):83-87.
[11]崔中兴.惯性导航系统[M].北京:国防工业出版社,1982.
[12]罗武胜,徐涛,杜列波.基于加速度计和磁强计的定向钻进姿态测量及方位校正[J].国防科技大学学报,2007,(1):106-110.

