基于双层Euler梁理论的土工格室加筋体变形计算*

张玲，程钦桂，赵明华

(湖南大学 土木工程学院，湖南 长沙 410082)

基于双层Euler梁理论的土工格室加筋体变形计算*

张玲†，程钦桂，赵明华

(湖南大学 土木工程学院，湖南 长沙 410082)

针对路堤工程中车辆荷载直接作用于路面板，再经路堤填土传递作用于土工格室加筋垫层的荷载传递实际，并考虑路堤填土刚度、地基土的排水固结效应对土工格室加筋体受力变形的影响，将土工格室加筋体视为置于Kelvin地基上的下梁、路面板视为置于Winkler地基上的上梁，基于双层Euler梁理论，建立考虑路面板-路堤-土工格室加筋垫层-地基土相互作用的上下梁挠曲变形微分方程并求解.将本文解答所得格室加筋体内力位移与传统弹性地基梁法计算结果进行比较，两者吻合良好.在此基础上，分析了格室体刚度、路堤填土刚度、地基反力系数、地基土固结度等因素对路面板及格室体挠曲变形的影响.结果表明：路面板及格室加筋垫层的挠曲变形会随着格室体刚度的增大及地基反力系数的增大而减小，随地基土固结度的增大而增大；此外，路堤填土刚度增大会减小路面板的挠曲变形但会增大格室加筋垫层的挠曲变形.

变形;土工格室加筋体；双层梁；Kelvin地基模型；Winkler地基模型

Abstract：For an embankment engineering，vehicle loads act on the pavement faceplate directly and then affect geocell reinforcement through the embankment fill.Considering this load transfer mechanism，and the effect of embankment fill stiffness and consolidation of soft soil，a geocell reinforced subgrade was regarded as a lower beam placed on Kelvin foundation and the pavement facelate was regarded as a upper beam placed on Winkler foundation.On the basis of the double-Euler-beam theory，a deformation control differential equation of geocell reinforcement and its solutions were proposed by taking into account the effect of the interaction among the pavement faceplate embankment fill，geocell reinforcement，and foundation soil.There is a good agreement when internal force and displacement calculated by the method in this paper are compared with internal force and displacement calculated by traditional method for elastic foundation beam.On this basis，the factors influencing the stress-deformation characteristics of the geocell reinforcement such as stiffness of geocell reinforcement，stiffness of embankment fill，coefficient of subgrade reaction force and the degree of consolidation of foundation soil,were discussed.The results show that flexural deformations of both pavement and geocell reinforcement reduce with the increment of stiffness of geocell reinforcement and the increment of coefficient of subgrade reaction force.And the deformations increase with the development of the consolidation of foundation soil.In addition，with higher embankment fill stiffness，the deformation of the pavement is smaller，while the deformation of geocell reinforcement is larger.

Keywords：deformation；geocell reinforcement；the double beam；Kelvin foundation model；Winkler foundation model

土工格室作为一种新型的土工合成材料，是由聚合物宽条带经由强力焊接或铆接键连接成的立体网状物.因其优异的工程性能而广泛应用于软土地基加固、路基边坡防护、高速公路扩建、路基支挡工程、沙漠地区筑路等工程中[1-7].

然而到目前为止，土工格室加筋地基的理论研究尚处于初级阶段，其变形计算尚无统一方法.而变形是路堤设计的一个重要参数，关于其计算方法也越来越受到学术界的重视.分析格室加筋地基受力变形时，可将其视为置于弹性地基上的有限长梁，采用弹性地基梁法进行计算.如赵明华等[8-9]视土工格室加筋垫层为弹性地基梁，提出了考虑筋土界面摩阻效应的土工格室加筋体的受力变形分析方法；张福海等[10]视土工格室加筋垫层为具有一定刚度的梁板，并提出了考虑水平抗力的双参数法土工格室加筋体的受力变形分析方法.但上述方法仍存在一些问题与不足，如将车辆荷载视为直接作用于格室加筋体上的集中荷载，并未考虑车辆荷载是直接作用于路面板，再经过路堤填土传递作用于格室体上的荷载传递实际情况，且不能反映路堤刚度对土工格室加筋体受力变形的影响.边学成等[11]视路基填料和地基土层为采用双参数的 Pasternak 模型，克服了传统 Winkler 地基模型无法考虑路基填料和地基中应力扩散的缺点，但未考虑地基土的排水固结效应.

因此，本文在前人研究的基础上，分别采用Winkler模型和Kelvin模型模拟路堤填料和地基土，基于双层Euler梁理论，视路面板为置于Winkler弹性地基的上梁，格室加筋体为置于Kelvin地基上的下梁，提出考虑路面板-路堤填土-土工格室加筋垫层-地基土之间相互作用的土工格室加筋体受力变形的计算公式，并给出相应解答.

1 模型的建立及公式推导

1.1 模型的建立

对如图1(a)所示的典型的路基路面结构进行分析，由上至下分别为：路面结构、路堤填土、土工格室加筋垫层和地基土.为简化计算，沿垂直路堤纵向取单位宽度的路基路面结构进行分析.视路面板为长2l1、刚度EI1的上梁、土工格室加筋垫层为长2l2、刚度EI2的下梁；车辆荷载为集中荷载，直接作用于路面板，再经由路堤填土作用于格室加筋垫层上.采用Winkler弹性地基模型模拟路堤填土，则其可提供的地基反力p1为：

p1=k1(y1-y2)

(1)

式中：y1为路面板的挠曲变形；y2为土工格室加筋垫层的挠曲变形；k1为路堤填土地基反力系数，其值与土的性质有关，可通过室内模型试验或现场载荷试验确定，也可查经验值表粗估[13].当路堤填土高度较小，可将路堤填土作薄压缩层处理，故k1取值参考文献[13]如式(2)所示：

(2)

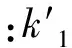
考虑垫层下地基土的排水固结效应影响，采用如图1(b)所示的Kelvin地基模型模拟地基土.根据太沙基有效应力原理，可得：

p2=σ′+ue

(3)

式中：p2为地基土可提供的总反力； σ′为有效应力；ue为t时刻的平均超孔隙水压力.

有效应力σ′可按式(4)计算：

σ′=k2y2

(4)

式中：k2为地基反力系数.

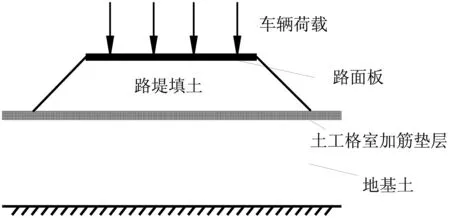
(a) 典型路堤工程横截面图

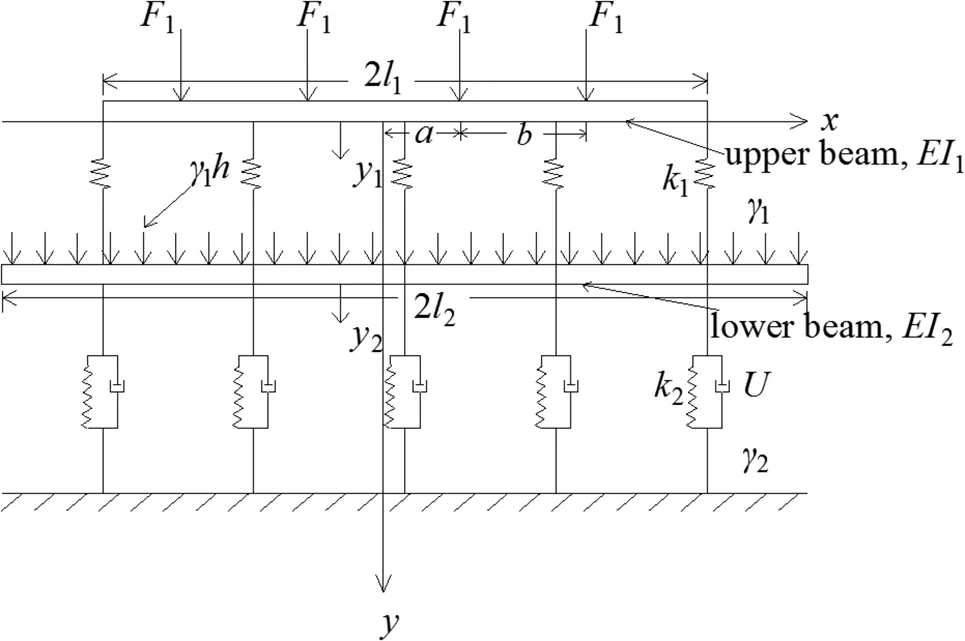
(b)沉降计算模型图 图1 路堤下土工格室加筋体沉降计算模型示意图

根据固结度的定义，t时刻的超孔隙水压力ue与t时刻地基的固结度U存在如下关系：

ue=u0(1-U)

(5)

式中：u0为初始孔隙水压力，u0=p2；固结度U可根据实际情况，采用一维或二维固结理论计算.

将式(4)，(5)代入式(3)，整理后可得：

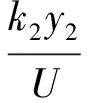
(6)

1.2 变形控制微分方程的建立及求解

根据对称原则，取路面板的中点为坐标原点，只对其右半部分(x≥0)进行分析.根据车辆集中荷载位置及上下梁的横截面尺寸，将梁的右半部分划分为若干段进行分析，第i段长度为li,(i=1,2,…,N-1)，第N段的长度为l2-l1.

当0≤x≤l1时，如图1所示，上梁(路面结构层)上表面作用有车辆荷载，下表面作用有路堤填土提供的地基反力；而下梁(土工格室加筋垫层)上表面除作用有因车辆荷载引起的Winkler弹簧(路堤填土)的反力外，还作用有来自路堤填土的自重.为简化计算，路堤填土的自重按面积相等原则将梯形分布荷载等效为均布矩形荷载，与此同时，下梁下表面受到地基土地基反力作用.分别在上梁和下梁取一微段进行受力分析，根据弹性地基梁理论，可得上梁、下梁挠曲变形控制微分方程分别为：

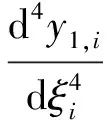
(7)

和

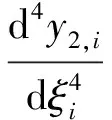
(8)

式中：EI1为路面板的抗弯刚度，EI2为土工格室的抗弯刚度.

将方程(7)变形后可得：

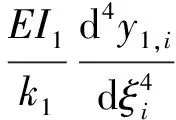
(9)

对方程(9)求4次导，并结合方程(8)，可得：

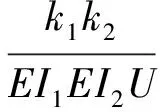
(10)

其通解为：

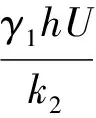
(11)

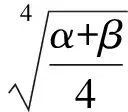
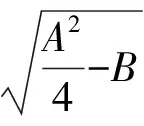
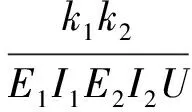
当li≤x≤l2时，由图1(b)可知，仅有下梁，此时下梁上表面仅作用路堤填土自重，可得其变形控制微分方程：

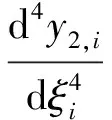
(12)

方程(12)可改写成：

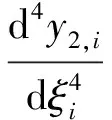
(13)

其通解为：

y2,i=eλ3ξi(D1,icosλ3ξi+D2,isinλ3ξi)+

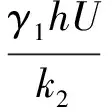
(14)

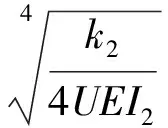
基于Euler-Bernoulli 梁理论，可得转角θi、弯矩Mi和剪力Qi如下：

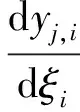
(15)

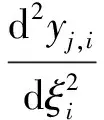
(16)

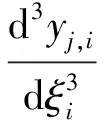
(17)

式中下标j=1表示上梁，j=2表示下梁，i=1，2，…，N.

式(11)中待定系数Cj,i(j=1，2，…，8；i=1，2，…，N-1)及式(14)中待定系数Dj,i(j=1，2，3，4；i=N)需通过以下边界和连续条件求得.

1)边界条件

(ⅰ)对于上梁，在x=0时，梁的转角和剪力都为0；在x=l1时，梁的弯矩和剪力为0.

(ⅱ)对于下梁，在x=0时，梁的转角和剪力都为0；在x=l2时，梁的弯矩和剪力为0.即：

对于上梁：

当x=0时，y1=0，Q1=0；

当x=l1时，M1=0，Q1=0；

对于下梁：

当x=0时，y2=0，Q2=0；

当x=l2时，M2=0，Q2=0；

2)连续条件

y1,i-1|ξi-1=li-1=y1,i|ξi=0；

θ1,i-1|ξi-1=li-1=θ1,i|ξi=0；

M1,i-1|ξi-1=li-1=M1,i|ξi=0;

Q1,i-1|ξi-1=li-1=Q1,i|ξi=0-F1.

y2,i-1|ξi-1=li-1=y2,i|ξi=0；

θ2,i-1|ξi-1=li-1=θ2,i|ξi=0；

M2,i-1|ξi-1=li-1=M2,i|ξi=0；

Q2,i-1|ξi-1=li-1=Q2,i|ξi=0.

结合边界条件和连续条件，求得待定系数，代入式(11)，(14)分别可得上、下梁任意点的挠曲变形，再由式(15)～(17)分别可得上、下梁任意点的转角，弯矩和剪力.

2 算例验证

为验证本文方法公式推导及编制程序的正确性，将本文方法所得下梁的内力位移计算结果与传统弹性地基梁法[13]计算结果进行比较.采用本文的双层梁理论分析计算传统单层地基梁时，为忽略上梁及路堤填土刚度的影响，分别取上梁的刚度、长度，地基填土刚度为一相对小值，参数取值具体如下：F1=100 kN作用于梁的中点，γ1=20 kN/m3，h=1 m，EI1=1 kN·m2，k1=0.01 kN/m2，l1=0.01 m，k2=12.5 MN/m2，EI2=208.33 MN·m2，l2=5 m.

两种方法的计算结果如图2～4所示.由图可见，忽略上梁影响时，本文方法计算所得的下梁挠曲变形y，转角θ，弯矩M与传统弹性地基梁法计算结果基本一致.

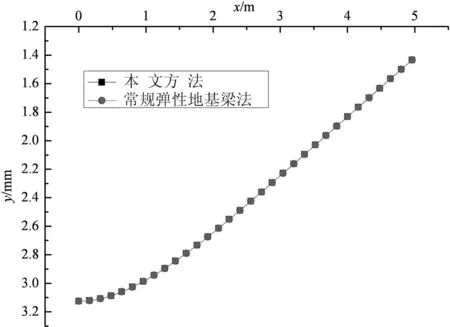
图2 两种方法挠曲变形y的比较

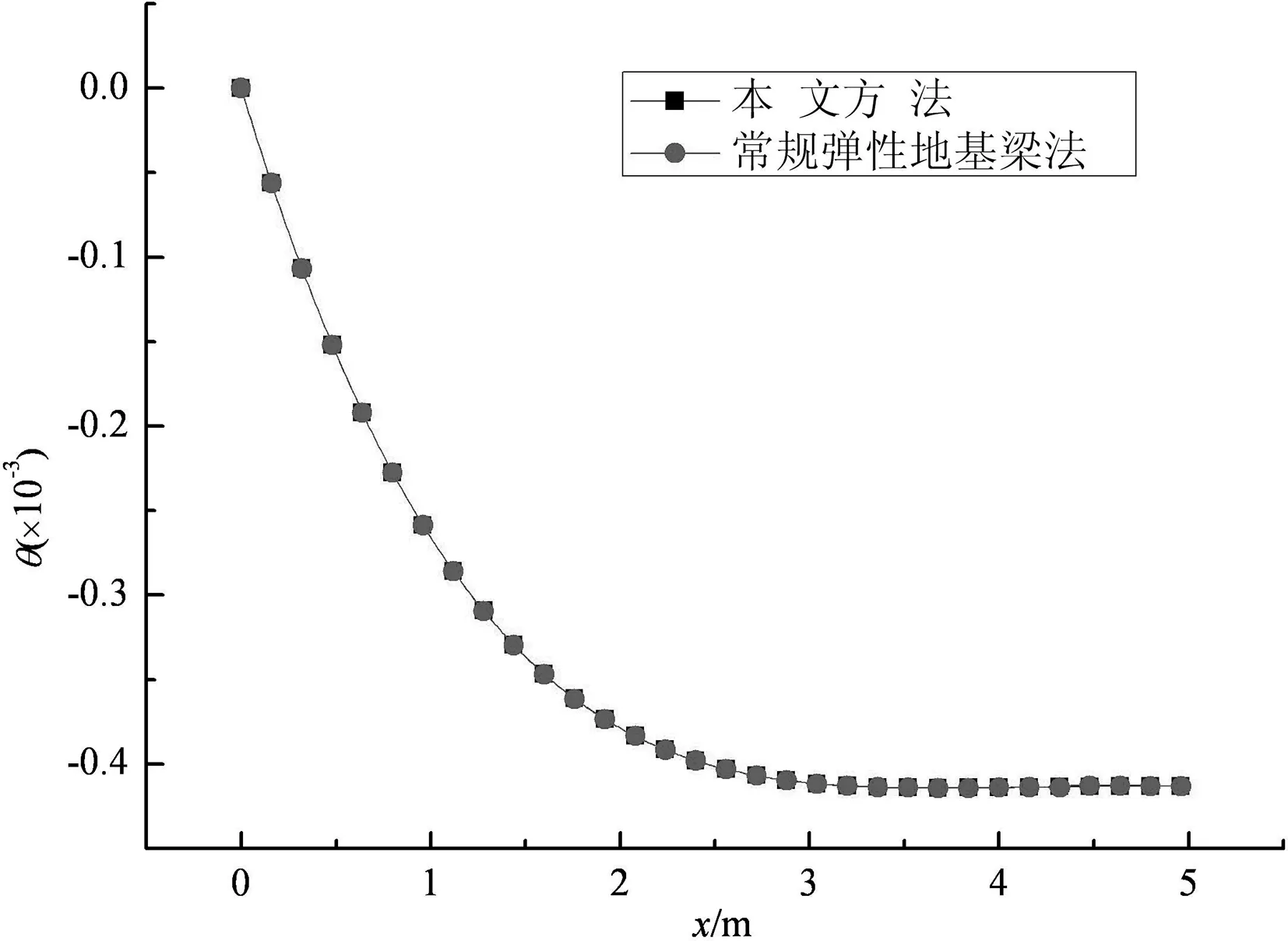
图3 两种方法转角θ的比较

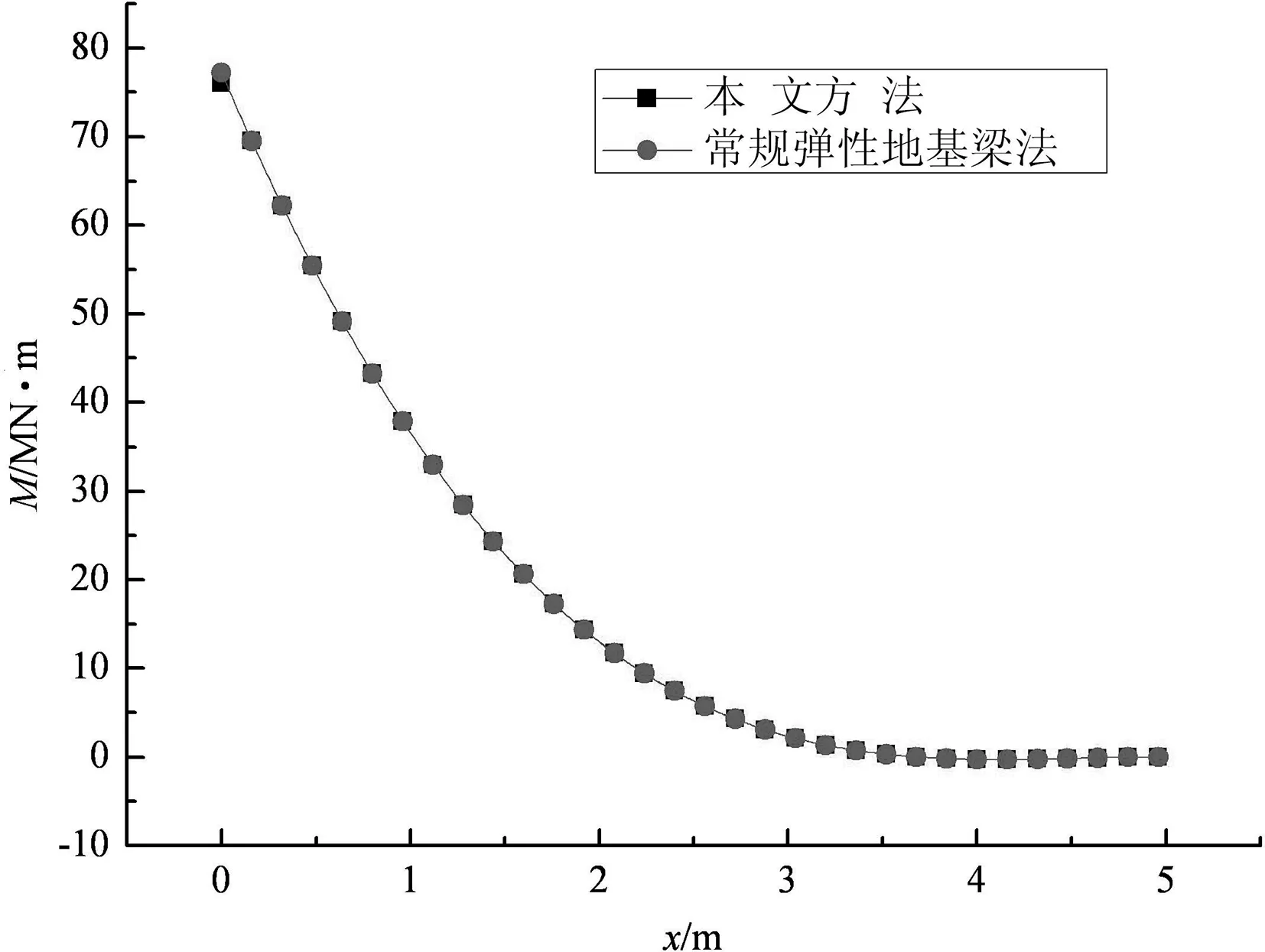
图4 两种方法弯矩M的比较

3 影响参数分析

为进一步分析土工格室加筋垫层的抗弯刚度EI2，路堤填土反力系数k1，地基土反力系数k2，地基土固结度U等因素对路面板中点和土工格室加筋垫层中点的挠度变形的影响，对某一路堤下格室加筋地基进行分析，基本计算参数如下：EI1=200 MN·m2，k1=50 MN/m2，l1=5 m，h=5 m，EI2=10 MN·m2，k2=5 MN/m2，l2=12.5 m，a=1.0 m，b=1.8 m，F1=50 kN，γ1=20 kN/m3，U=100%.

3.1 3种不同方法格室体变形的比较

图5为将车辆荷载等效为1 m高填土路堤、车辆荷载直接作用土工格室和本文双层梁法计算所得的路堤横截面上土工格室加筋垫层的挠曲变形.

由图5可见，对车辆荷载作不同的处理所得的格室体的挠曲变形有较大差异.将车辆荷载直接等效为一定高度的路堤填土自重，或直接将车辆荷载视为集中力作用于格室加筋垫层上，虽计算相对简便，可直接采用传统弹性地基梁分析，但均不能反映车辆荷载经由路面板、路堤填土扩散的实际，且结果与本文的双层梁理论所得的格室加筋体的挠曲变形差异较大.将车辆荷载直接等效为一定高度的路堤填土自重时，中心点处的挠曲变形偏小，且横截面上各点因车辆荷载引起的附加变形相等，这明显与实际情况不符.将车辆荷载视为集中力直接作用于格室加筋垫层上时，无疑又夸大了车辆荷载对格室加筋体受力变形的影响.因此本文基于双层地基梁理论所得的格室加筋体的挠曲变形因能反映车辆荷载-路面板-路堤填土-加筋垫层相互作用而更能符合实际情况.

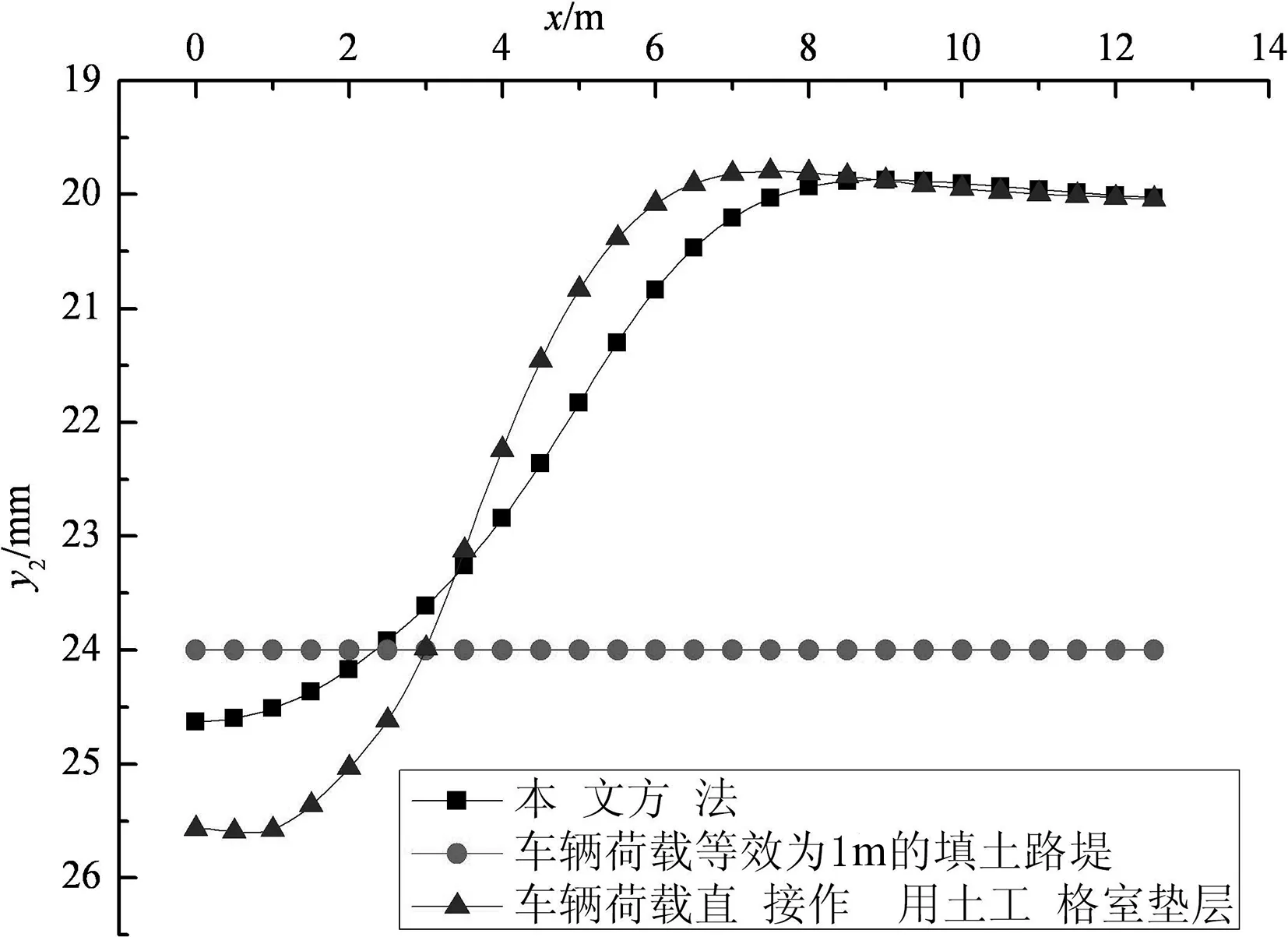
图5 3种方法挠曲变形y2的对比

3.2 土工格室加筋垫层抗弯刚度的影响

图6，图7分别为路面板中点的挠度变形y1,0、土工格室加筋垫层中点的挠度变形y2,0与土工格室加筋垫层抗弯刚度EI2的关系曲线.

由图6可见，当其它条件不变时，路面板中点的挠度变形随着土工格室加筋垫层抗弯刚度的增大而减小.当加筋垫层EI2从10 MN·m2增加到100 MN·m2时，路面板中点的挠度变形y1,0从25.09 mm减少到24.76 mm，减小幅度不大.

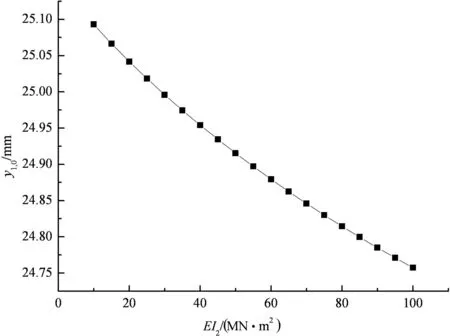
图6 y1,0与EI2的关系

由图7可见，当其它条件不变时，土工格室加筋垫层中点的挠度变形随着土工格室加筋垫层抗弯刚度的增大而减小，但减小幅度不大，当加筋垫层EI2从10 MN·m2增加到100 MN·m2时，土工格室加筋垫层中点的挠度变形y2,0从24.63 mm减少到24.30 mm.

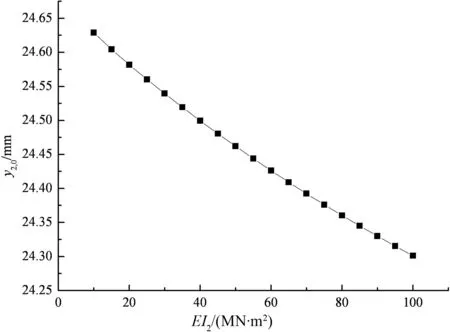
图7 y2,0与EI2的关系

对比图6、图7亦可见，由于荷载作用下，路堤填土自身的压缩性，路面板的挠曲变形略大于格室加筋垫层的挠曲变形.

3.3 路堤填土反力系数k1的影响

图8，图9为路面板中点的挠度变形y1,0、土工格室加筋垫层中点的挠度变形y2,0与路堤填土反力系数k1的关系曲线.

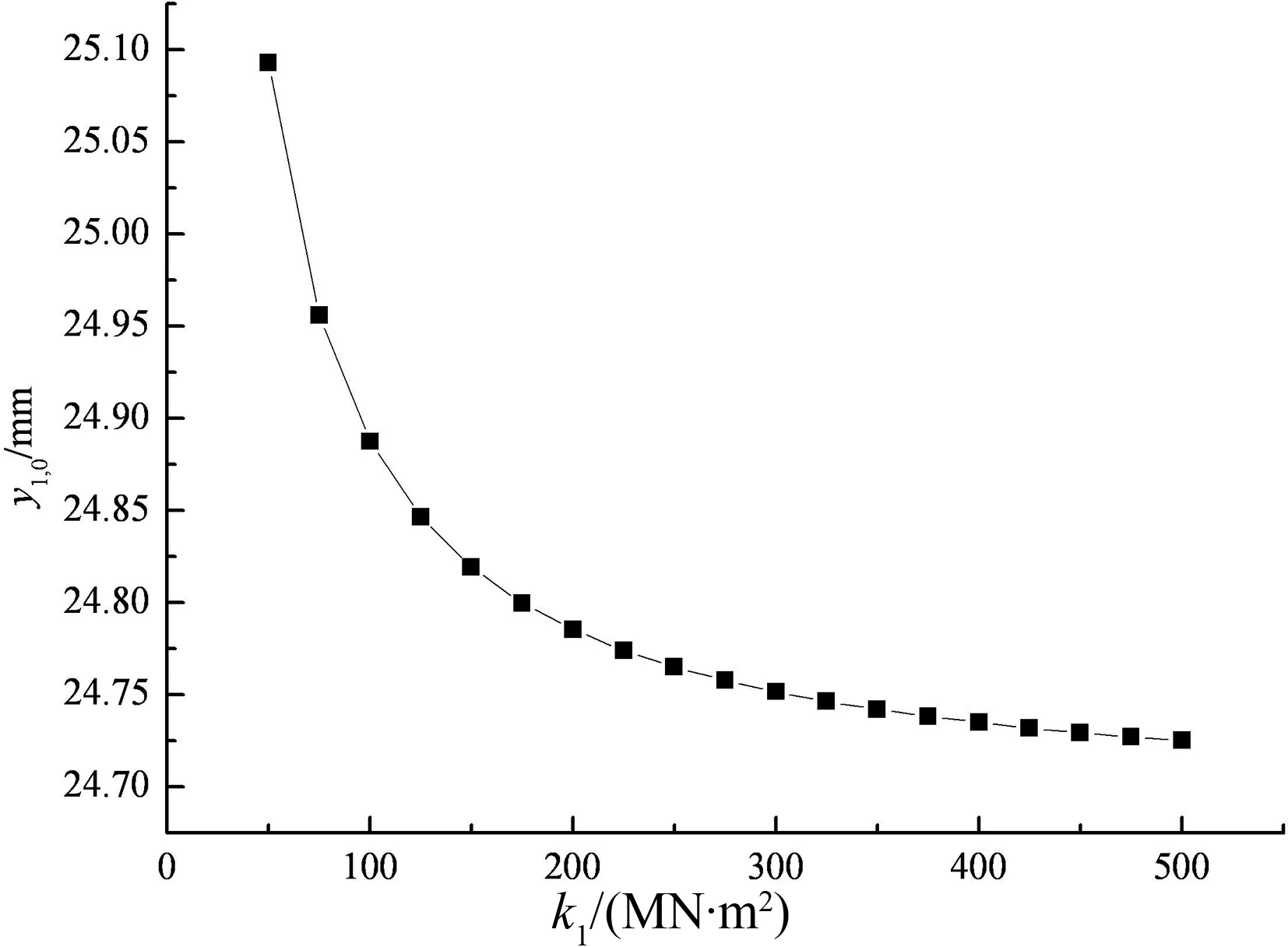
图8 y1,0与k1的关系

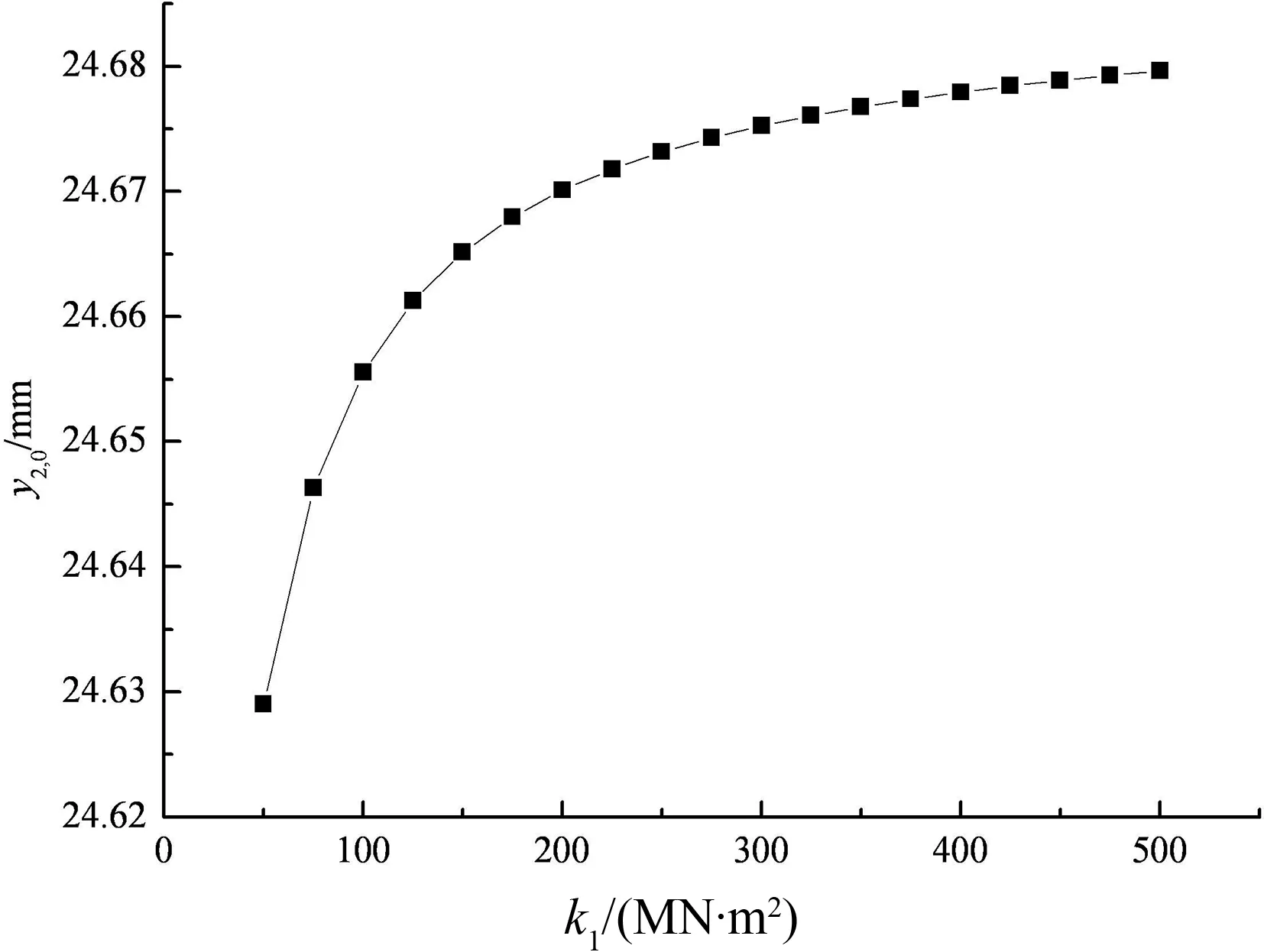
图9 y2,0与k1的关系

由图8，图9可见，当其它条件不变时，路面板中点的挠度变形随路堤填土反力系数的增大而减小；土工格室加筋垫层中点的挠度变形随着地基反力系数的增大而增大.当路堤填土反力系数k1从50 MN/m2增至500 MN/m2时，路面板中点的挠度变形y1,0从25.09 mm减少到24.73 mm，加筋垫层中点的挠度变形y2,0从24.63 mm增加到24.68 mm，变化幅度都不大.其原因可能是路堤填土密实度等物理力学特性越好，路堤填土反力系数越大，其可提供的竖向反力也越大，路面板就越不易产生挠曲变形，故路面板中点挠曲变形也就随路堤填土反力系数k1的增大而逐渐减小.而路堤填土地基反力系数越大，填土刚度越大，经路堤Winkler弹簧作用于格室体上反力越大,相应的挠曲变形也就越大，故格室体中点挠曲变形反而随路堤填土反力系数k1的增大而增大.

3.4 地基反力系数k2的影响

图10，图11为路面板中点的挠度变形y1,0、土工格室加筋垫层中点的挠度变形y2,0与地基反力系数k2的关系曲线.

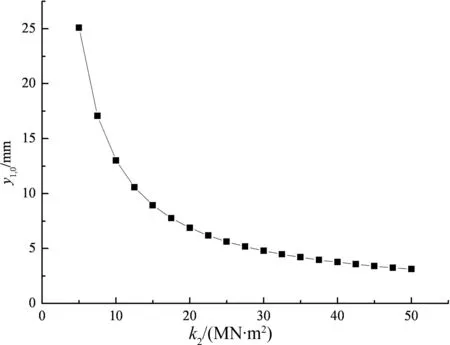
图10 y1,0与k2的关系

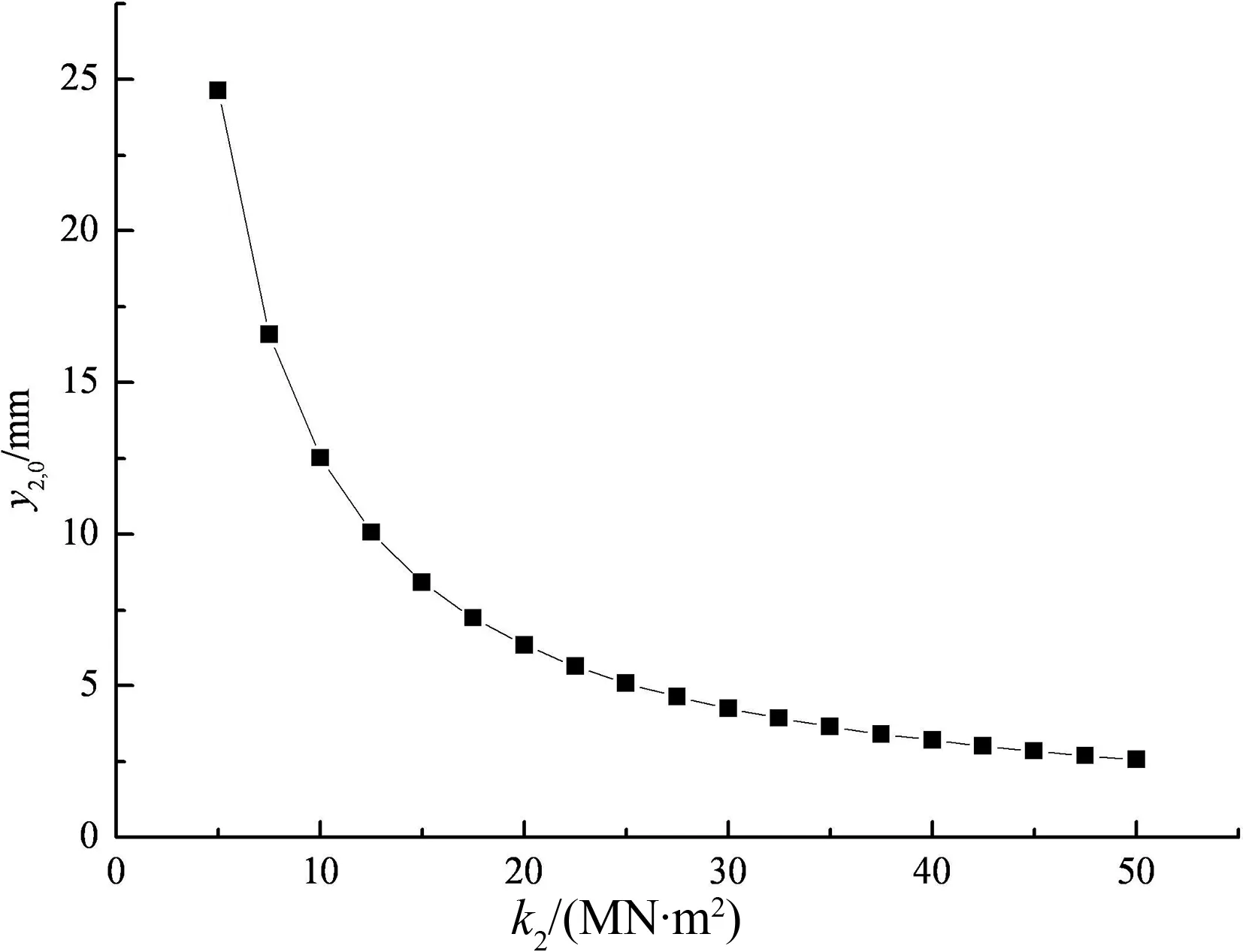
图11 y2,0与k2的关系

由图10，图11可见，当地基反力系数k2从5 MN/m2增至50 MN/m2时，路面板中点的挠度变形y1,0从25.09 mm.减少到3.12 mm，加筋垫层中点的挠度变形y2,0从24.63mm减少到2.56mm.其原因是当其它条件不变时，由于地基土物理力学特性越好，强度越大，从而地基反力系数越大，其可提供的竖向反力也越大，因此，路面板中点和土工格室加筋垫层中点的挠度变形都随着地基反力系数的增大而减小.但其对挠曲变形减小的趋势是先随k2的增加减小幅度较大，当k2大于某一值时，减小的幅度逐渐变小.如图10～图11，k2从5 MN/m2增至35 MN/m2时，y1,0从25.09 mm减少到4.20 mm，减小了83%，y2,0从24.63 mm减少到3.65 mm，减小了85%；但当k2从35 MN/m2增至50 MN/m2时，y1,0从4.20 mm减少到3.12 mm，减小了26%，y2,0从3.65 mm减少到2.56 mm，减小了30%.

由此可见，合理提高地基反力系数是控制路基过量沉降的有效措施之一，但当地基反力系数大于某一值时，提高地基反力系数对减小路基路面沉降的作用不再明显.

3.5 地基土固结度的影响

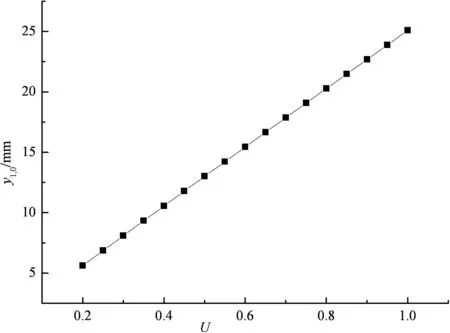
图12 y1,0与U的关系

图12，图13为路面板中点的挠度变形y1,0、土工格室加筋垫层中点的挠度变形y2,0与地基土固结度U的关系曲线.对于饱和软粘土地基，当其它条件不变时，随着时间的推移，地基土排水固结，固结变形不断增大，从而使得路面板中点和土工格室加筋垫层中点的挠度变形都随着地基土固结度的增大而增大.由图12，图13可见，当固结度U从20%增至100%时，路面板中点的挠度变形y1,0从5.62 mm增加到25.09 mm，加筋垫层中点的挠度变形y2,0从5.09 mm增加到24.63 mm.

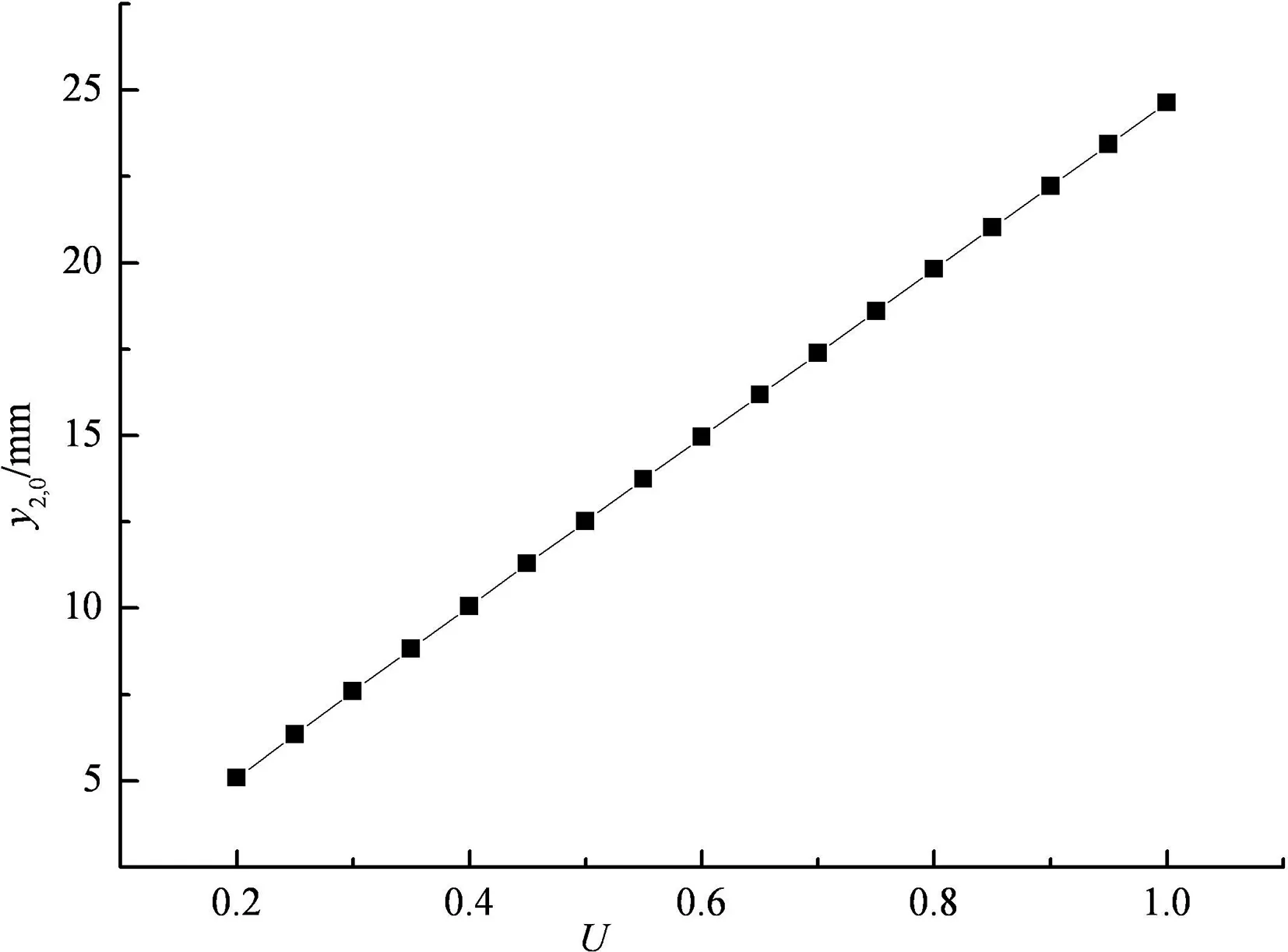
图13 y2,0与U的关系

4 结 语

1)将土工格室加筋路堤中的路面板结构视为上梁，土工格室加筋垫层视为下梁，采用Winkler弹性地基模型模拟路堤填土，Kelvin地基模型模拟垫层下地基土以考虑地基土体随时间的排水固结作用，基于Euler双层梁理论导得土工格室加筋体的挠曲变形微分方程，并获得解析解.通过与传统弹性地基梁法计算结果的比较分析验证了本文解答的正确性.

2)本文挠曲变形计算方法从车辆荷载是直接作用路面板结构，并经由路堤填土传递至格室加筋垫层，再通过加筋垫层作用于地基土的这一荷载传递实际出发，可考虑路面板-路堤填土-土工格室加筋垫层-地基土之间的相互作用对土工格室挠曲变形的影响.

3)基于本文理论，探讨分析了格室体刚度、路堤填土刚度、地基土刚度、地基土固结度等4个因素对路面板结构及土工格室加筋垫层受力变形的影响，研究表明：格室体刚度增大10倍，路面板结构及格室加筋垫层的挠取变形减小值在5%以内；但地基反力系数增大10倍，路面板结构及格室加筋垫层的挠取变形减小值在80%以上.因此在实际设计过程中可优先考虑通过有效地基处理增大地基土的刚度以达到减小路面沉降的目的.

[1] 刘金萍，黄安荣，石文建.土工格室的作用机理与工程应用现状[J].黑龙江交通科技，2015(8)：17-18.

LIU Jinping，HUANG Anrong，SHI Wenjian.The reinforc-ement mechanism and status in engineering application of geocell [J].Heilongjiang Science & Technology of Communications,2015(8)：17-18.(In Chinese)

[2] 李力，傅舰锋.土工格室作用机理与应用研究现状[J].山西交通科技，2003(S1)：63-65.

LI Li,FU Jianfeng.The reinforcement mechanism and status in applicationand study of geocell [J].Shanxi Science and Technology of Communications,2003 (S1)：63-65.(In Chinese)

[3] 张胜， 赵华宏.土工格室在软土地基处理中的应用与研究[J].公路交通科技，2004，21(4)：37―39，46.

ZHANG Sheng，ZHAO Huahong.Study on application of cellular geogrid system in soft ground treatment [J].Journal of Highway and Transportation Research and Development,2004，21(4)：37―39，46.(In Chinese)

[4] 郭庆淀，顾跃强，张立杰.高强土工格室在高速公路路基施工中的应用[J].山西建筑，2009，35(4)：298-299.

GUO Qingdian，GU Yueqiang，ZHANG Lijie.The high intensity geogrid application in express highway foundation construction [J].ShanXi Architecture,2009，35(4)：298-299.(In Chinese)

[5] 宗军良.土工格室加筋路基作用机理与应用技术探讨[J].路基工程，2011(3)：107-109.

ZONG Junliang.Discussion on action mechanism and application technology of geogrid reinforced subgrade[J].Subgrade Engineering，2011(3)：107-109 .(In Chinese)

[6] 杜勇立，高礼，杨果林.不同掺土量加筋煤矸石的界面摩擦试验研究[J].湖南大学学报：自然科学版，2014，41(4)：54-60.

DU Yongli,GAO Li,YANG Guolin.Experimental study of the interface friction characteristics between coal gangue and reinforcement with different qualities of soil [J].Journal of Hunan University：Natural Sciences，2014,41(4)：54-60.(In Chinese)

[7] 蒋德松，蒋冲.城市岩质边坡土工格室生态防护技术及其应用[J].湖南大学学报：自然科学版 ，2008，35(11)：12-16.

JIANG Desong ,JIANG Chong.Geotechnical grid bio-engineering protection of the rockmass slope in the city and its application[J].Journal of Hunan University：Natural Sciences,2008，35(11)：12-16 .(In Chinese)

[8] 赵明华，张玲，马缤辉,等.考虑水平摩阻效应的土工格室加筋体受力分析[J].工程力学，2010，27(3)：38-44.

ZHAO Minghua ，ZHANG Ling ，MA Binhui,etal.Force analysis of geocell reinforcement with consideration of horizontal resistance effect [J].Engineering Mechanics，2010,27(3)：38-44.(In Chinese)

[9] 赵明华，张玲，曹文贵,等.基于弹性地基梁理论的土工格室加筋体变形分析[J].岩土力学，2009，30(12)：3695-3699.

ZHAO Minghua，ZHANG Ling，CAO Wengui，etal.Deformation analysis of geocell reinforcement based on theory for beam on elastic foundation [J].Rock and Soil Mechanics,2009，30(12)：3695-3699 .(In Chinese)

[10] 张福海，俞仲泉.平面应变条件下土工格室加筋垫层的变形分析[J].岩土力学，2005(S1)：245-247.

ZHANG Fuhai，YU Zhongquan.Analysis of deformation of geocell reinforced mat under plane strain condition [J].Rock and Soil Mechanics,2005(S1)：245-247.(In Chinese)

[11] 边学成，宋广，陈云敏.Pasternak地基中土工格室加筋体的受力变形分析[J].工程力学，2012，29(5)：147-155.

BIAN Xuecheng ，SONG Guang ，CHEN Yunmin.Deformation behaviors of geocell reinforcement in Pasternak ground [J].Engineering Mechanics，2012，29(5)：147-155 .(In Chinese)

[12] 钱家欢，殷宗泽.土工原理与计算[M].北京：中国水利水电出版社,1996:414-417.

QIAN Jiahuan ，YIN Zongze .Principle and calculations of civil engineering[M].Beijing：China Water and Power Press,1996:414-417 .(In Chinese)

[13] 龙驭球.弹性地基梁的计算[M].北京：人民教育出版社,1981:6-12.

LONG Yuqiu .Calculation of the elastic foundation beam[M].Beijing：People’s Education Press,1981:6-12 .(In Chinese)

Deformation Calculation of Geocell Reinforcement Based on the Double Euler Beams Theory

ZHANG Ling†，CHENG Qingui，ZHAO Minghua

(College of Civil Engineering，Hunan University，Changsha 410082，China )

1674-2974(2017)09-0114-08

10.16339/j.cnki.hdxbzkb.2017.09.014

2016-07-23

国家自然科学基金资助项目(青年基金)(51208191)，National Natural Science Foundation of China(51208191)

张玲(1982-)，女，浙江临海人，湖南大学副教授，博士

†通讯联系人，E-mail：zhanglhd@163.com

TU443

A