超高性能轻型组合桥面设计指标近似计算方法*
李嘉,曾玉,易笃韬,邵旭东
(1.湖南大学 土木工程学院,湖南 长沙 410082;2. 中交第四航务工程勘察设计院有限公司,广东 广州 510000; 3. 风工程与桥梁工程湖南省重点实验室,湖南 长沙 410082)
超高性能轻型组合桥面设计指标近似计算方法*
李嘉1†,曾玉1,2,易笃韬1,3,邵旭东1,3
(1.湖南大学 土木工程学院,湖南 长沙 410082;2. 中交第四航务工程勘察设计院有限公司,广东 广州 510000; 3. 风工程与桥梁工程湖南省重点实验室,湖南 长沙 410082)
在有限元建模的基础上,通过正交试验设计,分别得到UHPC层最大拉应力、表面局部挠跨比和栓钉最大剪应力等结构设计指标的关键影响因素.采用拉丁超立方抽样方法,探究结构设计指标与各自的关键因素之间的内在联系,建立UHPC最大拉应力、表面局部挠跨比和栓钉最大剪应力的近似计算公式.对近似计算公式进行统计检验、经验判断及足尺模型、推出模型试验检验.研究表明:本文提出的设计指标近似计算公式,其线性相关与回归效果显著,且定性分析与一般工程经验相符,3个指标计算值与试验实测值的相对误差小于10%.
超高性能轻型组合桥面;近似计算;有限元;正交试验;拉丁超立方抽样
Abstract:For the purpose of engineering application of High-Performance Lightweight Composite Bridge Decks,it was necessary to study the approximate calculation method of structural design indices. On the basis of finite element modeling,orthogonal tests were designed to obtain the key factors influencing the maximum tensile stress of UHPC,the ratio of local deflection on bridge deck,and shear stress of stud. The Latin hypercube sampling method was used to find out the internal relations between structural design indices and their key factors. Approximate calculation formulas of the maximum tensile stress of UHPC,the ratio of local deflection ,and shear stress of stud were presented,which were examined by statistical tests,judgments based engineering experiences- full-scale model tests and push-out model tests The results show that the linear correlations and regression effects of the formulas were significant,and the qualitative analysis were consistent with the general engineering experiences. The relative error between the calculated value of the three indexes and the measured value is less than 10%. They are of good applicability.
Keywords:high-performance lightweight composite bridge decks ; approximate calculation; finite element; orthogonal experiment;Latin hypercube sampling
目前,国内外的钢桥面铺装通常采用柔性铺装或刚性铺装,其中柔性铺装凭借其自重轻、行车舒适等优点而被大量使用.然而,由于环氧沥青混凝土、SMA和浇筑式沥青混凝土等在重载、高温等作用下容易出现铺装层开裂、车辙、层间脱空等问题,且柔性铺装材料刚度较低,钢桥面结构局部应力幅较大,容易出现疲劳开裂[1-3].刚性铺装能提高桥面刚度,但存在厚度大、材料抗拉强度不足等缺点,不能广泛应用于大跨径钢桥[4].为综合解决钢桥面疲劳裂纹和铺装易损坏两大问题,作者研究团队提出超高性能轻型组合桥面,即将活性粉末混凝土(Reactive Powder Concrete,简称RPC)进行材料优化和密集配筋,形成适应钢桥面受力要求的超高性能混凝土(Ultra-high Performance Concrete,简称UHPC),UHPC与钢桥面板构成组合结构,其上铺筑薄磨耗层,钢面板以上总厚度为41~68 mm.前期研究表明:超高性能轻型组合桥面可以有效降低钢桥面结构的应力及变形、改善铺装层的受力状况,从而消除钢桥面疲劳开裂及铺装层开裂、车辙等风险[4-5].
超高性能轻型组合桥面已在广东马房大桥、广东佛陈大桥、北京通惠河大桥、天津海河大桥等投入使用.为了方便新技术的工程应用,有必要研究结构设计指标的近似计算方法.本文采用正交设计方法进行参数敏感性分析,运用拉丁超立方抽样法与数值仿真,分析设计控制指标与其关键参数的相关关系,提出UHPC层最大拉应力、表面局部挠跨比及栓钉剪应力的近似计算公式,并对其精确性进行检验,为制定设计规程提供技术支持.
1 有限元计算模型
以典型正交异性钢箱梁段为计算原型(图1),使用通用有限元计算软件ANSYS,建立“钢-UHPC-磨耗层”局部有限元模型.
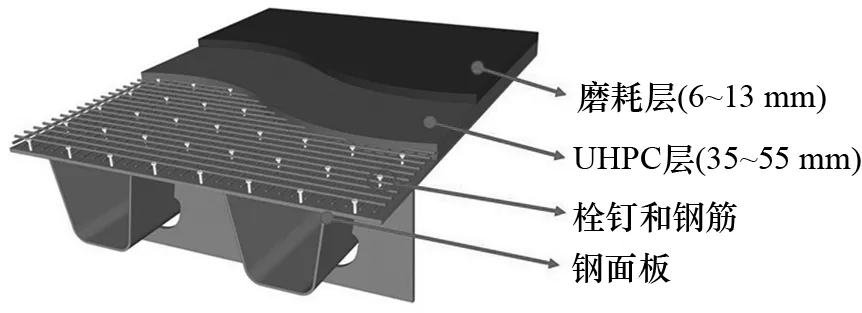
图1 正交异性轻型组合钢桥面
在横桥向选取6个U肋,纵桥向选择4块横隔板,有限元模型如图2所示.

图2 有限元整体模型和栓钉局部模型
在图2中,钢板采用4节点弹性壳单元SHELL63模拟,UHPC层与磨耗层均采用20节点实体单元SOLID95模拟,钢板与UHPC抗剪连接件为栓钉,栓钉采用SOLID45单元模拟,钢筋采用LINK8单元模拟.栓钉与UHPC交界处的节点完全耦合,栓钉最下端的节点与钢面板完全耦合,UHPC底面与钢面板顶面耦合竖直方向的自由度.为模拟混凝土与钢板间的自然粘结,钢板上表面和UHPC下表面分别建立TARGE170和CONTA173接触对单元,考虑0.2的切向摩擦系数与足够大的法向接触刚度,允许产生相对滑移,不允许相互穿透.边界条件为:钢桥面板、UHPC层和横隔板的顺桥向两侧完全固结;钢桥面顶板横桥向边缘无横向位移;横隔板下端约束纵、横向位移[6].
根据《公路桥涵设计通用规范》[7]选取局部分析所用计算荷载.由于正交异性桥面板明显的局部受力特性,在远离车轮荷载的部位受力不明显[8],故只施加轴重最大的一个轴的荷载,即施加一个140 kN轴重的后轴单轴轮载,加载面为两块200 mm× 600 mm的作用面积,并考虑30%的冲击作用.水平力为垂直荷载乘以0.5的水平系数[9].横、纵向荷载布置分别如图3、图4.
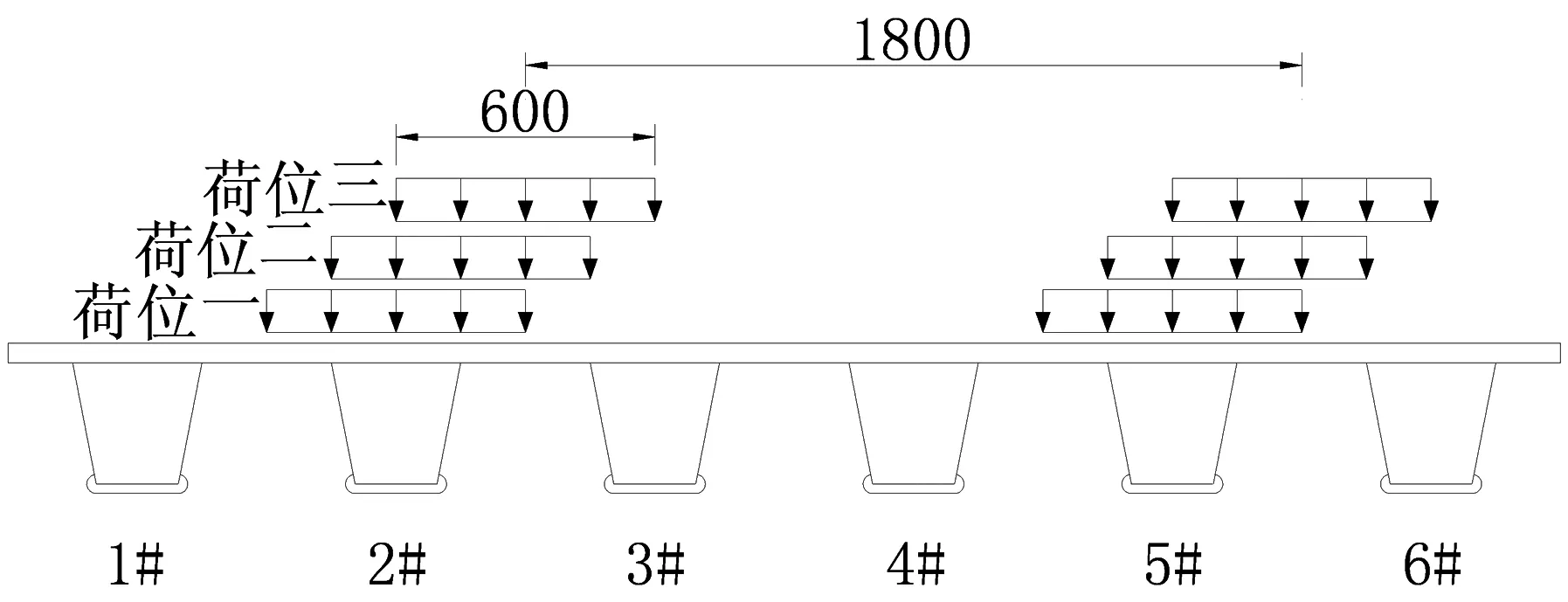
图3 钢桥横截面及荷载横桥向布置图(mm)

图4 荷载纵桥向布置图(mm)
2 结构设计指标及关键参数分析
试验表明,栓钉先于UHPC发生剪切破坏[10].本文以控制结构性破坏为目标,从轻型组合桥面的使用条件、工程实践、试验研究和受力特点等方面出发,选择UHPC层拉应力、表面局部挠跨比[11]、栓钉剪应力作为结构设计的控制指标.
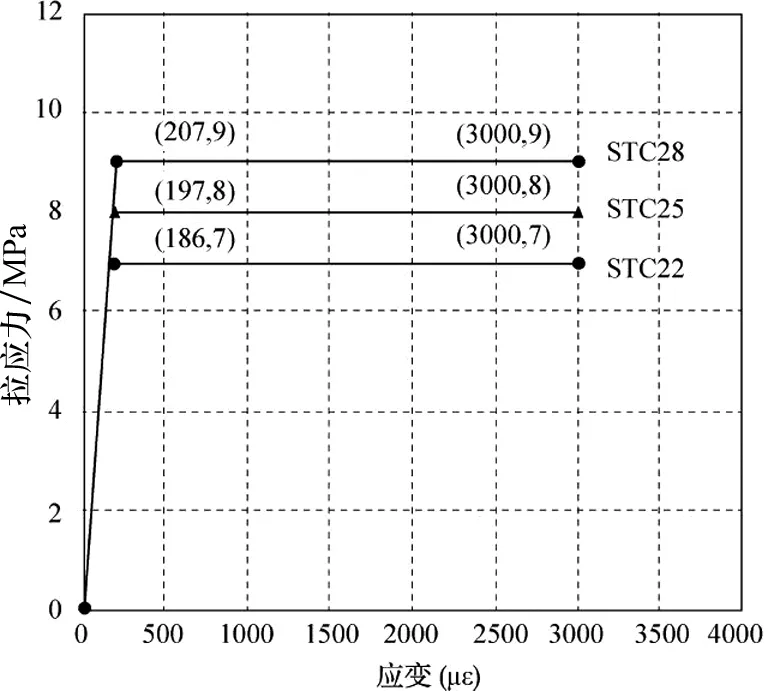
图5 不配筋UHPC的轴拉应力-应变曲线
参考欧洲规范4[12]和《超高性能轻型组合桥面结构技术规程》[9],影响正交异性钢桥面结构设计的相关因素多达13种,即:U肋间的距离d,U肋下宽b,U肋上宽u,U肋高h,U肋厚t,UHPC配筋率k,UHPC厚度T1、顶板钢板厚度T2、横隔板间距L、UHPC的弹性模量E、纵向荷位布置、横向荷位布置、栓钉直径D、栓钉间距s等.其中,钢筋直径为10 mm[9],配筋率由不同的钢筋间距计算可得.栓钉采用ML15号钢,其弹性模量取定值.不配筋的UHPC(原称STC)材料受拉应力-应变曲线如图5所示.图5中, STC22,STC25和STC28的轴拉强度设计值ftd分别取为7 MPa,8 MPa和9 MPa,极限拉应变设计值εtd取固定值3 000 με[9].
本文采用正交试验法确定结构设计指标的关键因素.基于目前国内外大跨径钢桥常用结构并参考相关规范,正交异性钢桥面结构设计参数常用取值范围见表1.

表1 结构设计参数取值范围
选择表1各参数的下限值、中间值 和上限值作为3个因素水平,即水平1、水平2和水平3,纵向荷位因素的水平1,2和3分别对应图4中的荷位1,2和3,横向荷位因素的水平1,2和3分别对应图3中的荷位1、2和3.按照正交表L27(313)进行正交试验(见表2),将表中各因素的水平值代入到有限元模型中,计算得到UHPC层最大拉应力σU、表面最大挠度值ξ以及栓钉最大剪应力τs,见表2.
2.1 有限元计算结果分析
以某次正交试验的有限元计算为例,分析各指标最大值出现的位置及其附近的应力分布情况.图6、图7分别为UHPC底面和栓钉的仰视图.从图6可看出,UHPC局部最大横向拉应力为12.988 MPa,出现在车轮边缘的UHPC底面靠近栓钉处.从图7可看出,栓钉最大剪应力19.381 MPa,出现在车轮区域内靠近边缘的栓钉根部.表面最大挠度0.658 mm,出现在左边及右边车轮中央.UHPC横向拉应力、栓钉剪应力均表现出很强的局部性,与峰值点的距离超过一个栓钉间距a处,其应力值迅速衰减至峰值的20%以下.
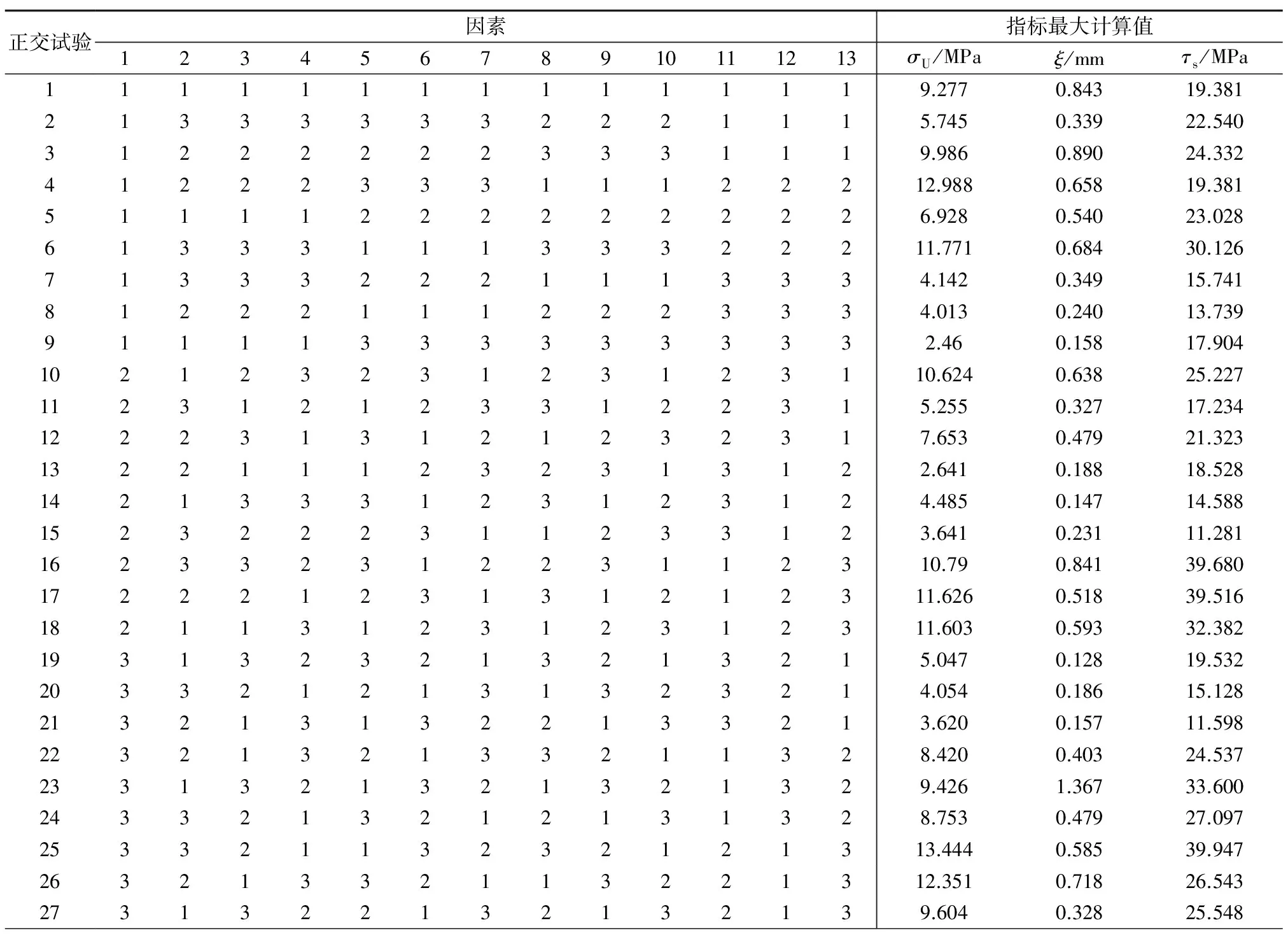
表2 UHPC拉应力及挠度值指标正交试验设计
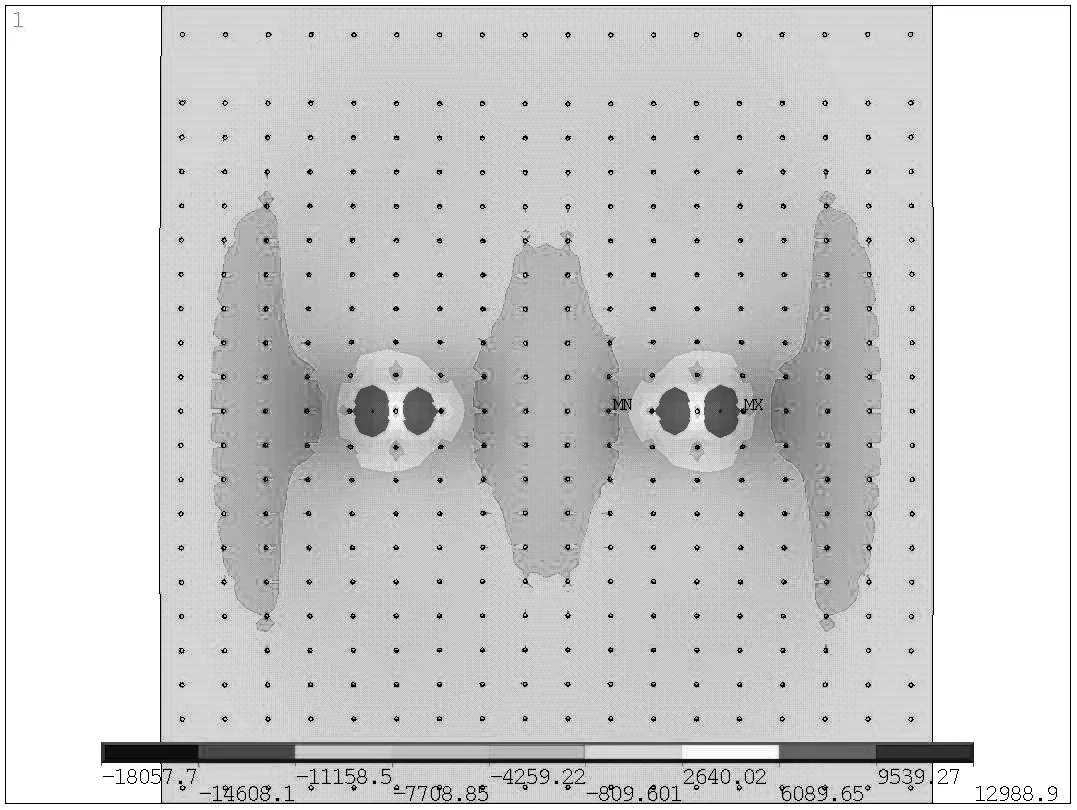
图6 UHPC横向拉应力分布图

图7 栓钉剪应力分布图
2.2 UHPC最大拉应力关键因素
文献[6]表明,UHPC横桥向受力较纵向更不利.故本文取UHPC最大横向拉应力作为结构设计指标.采用直观分析法对表2的正交试验结果进行极差分析,极差值R越大,说明该因素的影响越大,从而得到各因素影响程度排序,如表3所示.根据表3的排序,可知影响UHPC最大拉应力关键因素为:d,L,T1,E和T2.在纵向荷位这一列,K1最大,所以纵向最不利荷位是荷位1.同理,横向最不利荷位是荷位3.
2.3 局部挠跨比最大拉应力关键因素
采用直观分析法对表面局部挠跨比λ=ξ/L的正交试验结果进行极差分析,得到各因素影响大小排序,如表4所示.根据表4的排序,可知影响局部挠跨比关键因素为:T1,T2,L,d和h.在纵向荷位这一列,K1最大,所以纵向最不利荷位是荷位1.同理,横向最不利荷位是荷位3.
2.4 栓钉最大剪应力关键因素
采用直观分析法对栓钉最大剪应力的正交试验结果进行极差分析,得到各因素影响大小排序,如表5所示.根据表5的排序,可知影响局部挠跨比关键因素为:D,E,a.在纵向荷位这一列,K1最大,所以纵向最不利荷位是荷位1.同理,横向最不利荷位是荷位1.

表3 UHPC最大拉应力极差分析表
注:K1为某一因素水平为i时某一考核指标值得总和,极差R=Ki(max)-Ki(min).

表4 局部挠跨比极差分析表

表5 栓钉最大剪应力极差分析表
3 结构设计指标计算公式
为了探究UHPC最大拉应力σU、最大局部挠跨比λ和栓钉最大剪应力τs等结构设计指标与各自的关键因素之间的内在联系,需要对关键因素在其取值范围内进行更为均匀、细致的抽样.本文采用拉丁超立方抽样法(Latin Hypercube Sampling,简称LHS),它是一种多维分层抽样方法,基于均匀分布准则,保证采样点覆盖所有的采样区域,其抽样点分布既均匀又能快速达到收敛[13-14].
3.1 拉丁超立方抽样


注:FX(·)为累计概率分布函数,rand(0,1)为(0,1)内任一随机数,Φ-1(·)为标准正态累积分布的逆函数 图8 LHS抽样流程图
3.2 抽样及计算
根据图8编制抽样程序,分别得到各关键因素的抽样值,代入到有限元模型中计算,得到相对应的σU,λ和τs值.限于篇幅,仅列出σU的关键因素抽样和有限元计算结果,见表6.

表6 UHPC抽样与计算结果
3.3 结构设计指标数学模型
对关键因素抽样值、设计指标计算值取对数,表达如下:
ln(σUi);ln(d),ln(L),ln(T1),
ln(E),ln(T2),i=1,2,…,20
(1)
ln(λi);ln(T1),ln(T2),ln(L),
ln(d),ln(h),i=1,2,…,20
(2)
ln(τsi);ln(D),ln(E),ln(a),
i=1,2,…,20
(3)
设定式(1),(2)和(3)符合二次函数关系,即:
y=Xβ+ε
(4)
式中:y为结构设计指标的对数值;X为关键因素对数值的一次项、二次项和交叉项.
根据逐步回归方法,剔除那些对因变量贡献小或与其他独立变量相关性较大的变量,只取p个变量(p 3.3.1 UHPC最大拉应力模型 由式(1) 、式(4): ln(σU)=β0+β1ln2(d)+β2ln2(E)+ β3ln2(T2)+β4ln(L)·ln(T1)+β5ln(L)·ln(E) +β6ln(T2)×ln(E) (5) 设b0,b1,…,b6分别是上式参数β0,β1,…,β6的最小二乘估计,计算得式(5)的最小二乘估计值为: [b0,b1,b2,b3,b4,b5,b6]=[-0.874,0.046, -3.938,-0.154,-1.799,1.955,3.755] (6) 联立式(5)、式(6),得到UHPC最大拉应力计算公式: (7) 式(5)~(7)中:σU为UHPC最大拉应力;D为U肋间距;L为横隔板间距;T1为UHPC厚度;E为UHPC弹性模量;T2为顶板厚度. 3.3.2 表面局部挠跨比模型 由式(2)、式(4): ln(λ)=β0+β1ln(T1)+β2ln2(h)+β3ln(T1)× ln(T2)+β4ln(L)ln(T1)+β5ln(L)ln(T2)+ β6ln(d)ln(h) (8) 设b0,b1,…,b6分别是上式参数β0,β1,…,β6的最小二乘估计,计算得式(8)的最小二乘估计值为: [b0,b1,b2,b3,b4,b5,b6]=[-61.375,29.429, 0.136,-6.006,-1.746,2.715,0.028] (9) 联立式(8)、式(9),得到最大局部挠跨比计算公式: (10) 式(8)~(10)中:λ为最大局部挠跨比;T1为UHPC厚度;T2为顶板厚度;L为横隔板间距;d为U肋间距;h为U肋高. 3.3.3 栓钉最大剪应力模型 由式(3) 、式(4): ln(τs)=β0+β1ln2(E)+β2ln(a)ln(D)+β3ln(E)ln(a) (11) 设b0,b1,…,b3分别是上式参数β0,β1,…,β3的最小二乘估计,计算得式(11)的最小二乘估计值为: [b0,b1,b2,b3]=[2.464,-0.625,-0.137, 0.625] (12) 联立式(11)、式(12),得到栓钉最大剪应力计算公式: (13) 式(11)~(13)中:τs为栓钉最大剪应力;D为栓钉直径;E为UHPC弹性模量;a为栓钉间距. 为了检验UHPC最大拉应力计算公式(7)、表面局部挠跨比计算公式(10) 、栓钉最大剪应力计算公式(13)的可靠性,本文依次进行统计检验、经验检验、足尺模型试验检验. 4.1 统计检验 分别对式(7),(10),(13)进行F检验和复相关系数R检验,如表7所示. 表7 近似计算公式精度分析 表7表明,式(7),(10),(13)的回归效果及线性相关性显著. 分别用式(7),(10),(13)对原来的样本进行估计,将估计值与原值进行比较(图9). 图9 估计值与计算值比较 图9中,UHPC最大拉应力、局部挠跨比、栓钉最大剪应力的拟合值与有限元计算结果之间最大偏差分别为4.83%,4.88%和7.49%. 4.2 经验检验 由式(5),令y=ln(σU),求得UHPC表面最大拉应力与关键参数之间有如下规律: (14) (15) (16) (17) (18) 由式(14),(15)可知,U肋间距与横隔板间距增大均可导致整体结构刚度降低,使UHPC层最大拉应力增大.式(16),(18)则表明,顶板或UHPC厚度增大均可使UHPC层最大拉应力减小.式(17)表明,随着UHPC弹性模量增大,其最大拉应力也大幅增加. 由式(8),令y=ln(λ),求得表面局部挠跨比与关键参数之间有如下规律: (19) (20) (21) (22) (23) 由式(19),式 (20),钢板厚度与UHPC层的厚度增加均可使结构整体刚度增加,挠度和挠跨比都将减小.反之,由式(22),U肋间距增大导致整体结构刚度降低,从而挠跨比增大. 由式(11),令y=ln(τs),求得栓钉最大剪应力与关键参数之间有如下规律: (24) (25) (26) 由式(24)可知,栓钉间距增大时,栓钉受到的剪应力也增大.由式(25),式(26),当栓钉直径或UHPC弹性模量增大时,使栓钉最大剪应力减小.这些规律均与《超高性能轻型组合桥面结构技术规程》相一致. 检验说明上述规律均与一般工程经验相符. 4.3 试验检验 4.3.1 足尺模型试验检验 为测试超高性能轻型组合桥面的各关键结构指标,以广东佛陈新桥为原型,横向选择7个U肋,纵向选择4块横隔板,制作1∶1足尺试验模型,如图10所示.足尺模型主要参数如表8所示. 图10 足尺模型试验 考虑到佛新大桥实际的运营环境和交通状况,荷载选择最大轮重为70 kN,加载面积为0.6 m×0.2 m,采用千斤顶逐级加载,加载级别为:70 kN(1倍轮载)→91 kN(1.3倍轮载)→140 kN(2倍轮载)→210 kN(3倍轮载).本试验在常温(25 ℃)条件下进行. 当试验加载力为91 kN(1.3倍轮载),纵、横向加载位置分别为跨中(荷位1)、U肋间(荷位3)时,实测得到UHPC最大横向拉应力为6.51 MPa,面层最大挠度为ξ=0.253 mm,实测表面局部挠跨比为λ=ξ/L=1.01×10-4. 表8 足尺模型主要参数 将表8中的各项参数代入到式(7),式(13)中,分别得到σU,λ的计算值,见表9. 表9 足尺模型试验值与近似计算公式计算值对比 由表9可知,式(7)、式(13)的计算值与实测值相对误差小于10%. 4.3.2 推出模型试验检验 根据图7所示的有限元计算结果分析可知,栓钉剪应力均表现出很强的局部性.为测试栓钉剪应力指标,本研究团队制作了图11所示的推出试验模型[15],其中图11(a)的左右两侧各有4个栓钉.模型各参数如表10所示. 将表10的各参数代入到式(7)中计算可得τs=24.78 MPa,同时将各参数代入到图2的有限元模型中计算得到滑移量为0.050 mm。 (a)试验加载 ( b)栓钉尺寸 图11 推出试验 栓钉间距a/mm栓钉直径D/mmUHPC弹性模量/GPa栓钉弹性模量/GPa1201342.6206 由力学计算可知,受剪的2个相同的栓钉,若它们的滑移量相同,那么其根部最大剪应力也相同.试验中滑移量为0.05 mm时,加载力为24.0 kN,计算得栓钉平均剪应力为τ实=22.61 MPa,式(7)的计算值比实测值大9.6%.实测值偏小的主要原因是平均剪应力τ实小于栓钉所受的最大剪应力. 上述统计检验、经验检验、足尺模型实测检验表明:本文提出的UHPC最大拉应力计算公式、表面局部挠跨比计算公式、栓钉最大剪应力计算公式的线性相关与回归效果显著,且符合钢结构的一般经验规律,是合理和可行的. 1)正交试验直观分析和方差分析表明,影响UHPC最大拉应力的关键因素为:U肋间距、横隔板间距、UHPC厚度、UHPC弹性模量、顶板厚度.影响局部挠跨比的关键因素为:UHPC厚度、顶板厚度、横隔板间距、U肋间距、U肋高度.影响栓钉最大剪应力的关键因素为:栓钉直径、UHPC弹性模量、栓钉间距. 2)本文提出的UHPC最大拉应力近似计算公式、表面局部挠跨比、栓钉最大剪应力近似计算公式,其回归效果及线性相关性显著,且与一般工程经验相符. 3)UHPC最大拉应力计算值和表面局部挠跨比计算值与足尺模型试验实测值的偏差、栓钉剪应力计算值与推出试验实测值的偏差均小于10%,证明近似计算公式具有较高的精度. [1] 黄卫.大跨径桥梁钢桥面铺装设计[J]. 土木工程学报,2007,40(9):65-77. HUANG Wei. Design of deck pavement for long-span steel bridges[J].China Civil Engineering Journal,2007,40(9):65-77.(In Chinese) [2] ROMAN WOLCHUK. Lessons from weld cracks in orthotr-opic decks on three european bridges [J]. Journal of Structural Engineering,1990,116(1):75-84. [3] RASMUS W,JOHN F O,STAN H,etalAnalysis of an orthotropic deck stiffened with a cement-based overlay [J]. Journal of Bridge Engineering,ASCE,2007,12(3):350-363. [4] 李嘉,冯啸天,邵旭东,等. 正交异性钢桥面-RPC薄层组合铺装体系研究[J]. 湖南大学学报:自然科学版,2012,39(12):7-12. LI Jia,FENG Xiaotian,SHAO Xudong,etal. Research on composite paving system with orthotropic steel bridge deck and thin RPC layer [J]. Journal of Hunan University:Natural Sciences,2012,39(12):7-12. (In Chinese) [5] SHAO Xudong,YI Dutao,HUANG Zhengyu,etal. Basic performance of the composite deck system composed of orthotropic steel deck and ultrathin RPC layer [J]. ASCE’s Journal of Bridge Engineering,2013,18(5):417-428. [6] 张阳,鲍超,刘榕. 预制RPC柱降低大跨PC刚构桥跨中长期下挠分析[J]. 湖南大学学报:自然科学版,2016,43(3):8-14. ZHANG Yang,BAO Chao,LIU Rong. Analysis of precast RPC column on reducing long-term mid-span deflection of rigid frame bridge. [J]. Journal of Hunan University:Natural Sciences,2016,43(3):8-14. (In Chinese) [7] JTG D60-2015 公路桥涵设计通用规范[S].北京:人民交通出版社,2015:26-28. JTG D60-2015 General code for design of highway bridge and culverts[S]. Beijing:China Communications Press,2015:26-28. (In Chinese) [8] 李雪莲.正交异性钢桥面复合铺装结构研究[D].长沙:长沙理工大学交通运输工程学院,2008:40-54. LI Xuelian. The study on characters of bearing and fatigue of the asphalt pavement on orthotropic steel bridge deck[D]. Changsha:School of Traffic and Transportation Engineering in Changsha University of Science & Technology,2008:40-54. (In Chinese) [9] GDJTG/T A01-2015 超高性能轻型组合桥面结构技术规程[S].北京:人民交通出版社,2015:8-48. GDJTG/T A01-2015 Technical specification for ultra-high performance light-weighted composite deck structure [S]. Beijing:China Communications Press,2015:8-48. (In Chinese) [10] 邵旭东,周环宇,曹君辉. 钢-薄层RPC组合桥面结构栓钉的抗剪性能[J]. 公路交通科技,2013,30(4):34-39. SHAO Xudong,ZHOU Huanyu ,CAO junhui. Shear behavior of studs of composite deck system composed of steel and ultra-thin RPC layer[J]. Journal of Highway and Transportation Research and Development,2013,30(4):34-39. (In Chinese) [11] JTG D64-2015 公路钢结构桥梁设计规范[S].北京:人民交通出版社,2015:95-97. JTG D64-2015 Code for design of highway steel structure bridge[S]. Beijing:China Communications Press,2015:95-97. (In Chinese) [12] EN 1994 Eurocode 4:Design of composite concrete and steel structures[S]. Brussels,Belgium:European Committee for Standardization,2005:29-57. [13] OLSSONl A M J, SANDBERG G E. Latin hypercube sampling for stochastic finite element[J]. ASCE’s Journal of Engineering Mechanics,2002,128(1):121-125. [14] YIN Y H ,LIU M Q. Orthogonal latin hypercube designs for Fourier-polynomial models[J]. Journal of Statistical Planning and Inference,2013,143:307-314. [15] 李嘉,杨波,邵旭东,等.钢桥面-薄层CRRPC组合结构栓钉连接件抗剪疲劳性能研究[J]. 土木工程学报,2016,49(6):67-75. LI Jia,YANG Bo,SHAO Xudong,etal. Research on shear fatigue of studs for composite deck system of steel slab and thin CRRPC layer. [J]. China Civil Engineering Journal,2016,49(6):67-75. (In Chinese) Approximate Calculation of Design Indices for High-Performance Lightweight Composite Bridge Decks LI Jia1†,ZENG Yu1,2,YI Dutao1,3,SHAO Xudong1,3 (1. College of Civil Engineering,Hunan University,Changsha 410082,China; 2. CCCC-FHDI Engineering Co.,Ltd,Guangzhou 510000,China; 3. Key Laboratory of Wind Engineering and Bridge Engineering in Hunan Province,Changsha 410082,China) 1674-2974(2017)09-0001-09 10.16339/j.cnki.hdxbzkb.2017.09.001 2016-06-20 国家自然科学基金资助项目(51678229),National Natural Science Foundation of China(51678229) 李嘉(1962—),女,湖南长沙人,湖南大学教授 †通讯联系人,E-mail:lijia@hnu.edu.cn U416.2 A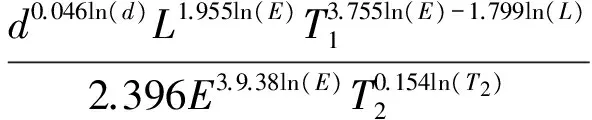

4 可靠性检验






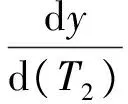
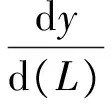

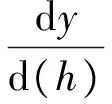
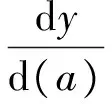







5 结 论

