考虑车-桥耦合振动及桥面平整度退化影响的拱桥吊杆疲劳分析*
殷新锋,丰锦铭,刘扬,蔡春声
(长沙理工大学 桥梁工程安全控制省部共建教育部重点实验室,湖南 长沙 410114)
考虑车-桥耦合振动及桥面平整度退化影响的拱桥吊杆疲劳分析*
殷新锋†,丰锦铭,刘扬,蔡春声
(长沙理工大学 桥梁工程安全控制省部共建教育部重点实验室,湖南 长沙 410114)
现有拱桥吊杆疲劳分析中,较少考虑车-桥耦合振动及考虑桥面平整度退化的影响,致使分析成果具有一定的局限性.根据在役桥面平整度等级国际通用评价体系,模拟了运营阶段桥面平整度退化历程.结合已编制随机车流-桥梁耦合振动分析程序,建立了可考虑车-桥耦合振动及考虑桥面退化等因素的拱桥吊杆疲劳分析模型.以某拱桥为工程背景,对比研究了不同因素作用下拱桥典型吊杆的疲劳损伤及疲劳寿命.结果表明,车-桥耦合振动及桥面平整度退化因素对拱桥吊杆疲劳影响较大,在考虑车-桥耦合及桥面平整度退化共同影响下,计算得到的吊杆疲劳寿命值比不考虑两者影响所得值少15~30年.研究成果对桥梁结构正常使用状态评估有一定的工程应用价值.
桥面平整度退化;车-桥耦合;吊杆;疲劳;随机车流
Abstract:The existing studies on the fatigue analysis for suspender of arch bridges have been found with limited consideration of the vehicle-bridge coupled vibration and road surface progressive deterioration,and those previous studies cannot reflect the actual fatigue property of the suspender.Based on the international general evaluation system of pavement roughness,a model of road surface progressive deterioration of each operation stage was established.A new model of fatigue analysis was then established by considering the effects of random traffic load model and road surface progressive deterioration.An arch bridge was taken as an example,and the differences of the fatigue performance analysis results for the typical suspender were analyzed and compared by the two situations with or without consideration of the conditions of the bridge deterioration and vehicle-bridge coupled vibration.Compared with the existing numerical method,the analysis results obtained by the proposed method show that the effects of vehicle-bridge couple vibration and road surface progressive deterioration on the suspender fatigue are significant,and the suspender fatigue value obtained by considering the above two factors can be improved by 15 years to 30 years.Therefore,the numerical results are significant for the maintenance of existing arch bridges.
Keywords:road surface progressive deterioration;vehicle-bridge coupled vibration;suspender;fatigue;stochastic traffic flows
拱桥吊杆是拱肋结构与桥面系之间的传力构件.现有在役拱桥吊杆疲劳性能研究中,常采用实桥试验及数值分析两种方法.实桥试验研究在时间、经济以及实现手段上存在诸多限制,致使试验研究较少采用,而常采用数值模拟分析.数值分析时常将疲劳荷载谱加载到拱桥模型中得到吊杆的应力谱,进而评估吊杆损伤及疲劳寿命值[1-3].
然而以往分析只考虑了交通量随时间的增长而忽略了车-桥耦合振动及桥面平整度退化等因素的影响[3-6].实际上在车辆荷载及其他不利环境因素的长期作用下,桥面在运营期间不断磨损甚至严重破坏,车辆超载率高的地区,桥面平整度退化速度已远超设计预测[5].然而部分桥面损坏严重的桥梁仍在继续服役,加剧了车辆与桥梁间动力相互作用,进而加剧了桥梁构件的疲劳损伤[7-10].
因此,更加精确的吊杆疲劳分析结果,需同时考虑车-桥耦合振动及桥面等级退化等参数的影响,并需建立新的考虑车-桥耦合的吊杆疲劳计算分析模型.本文根据国际通用的在役桥面平整度等级评价体系,建立了可模拟桥梁各个运营阶段桥面平整度的退化模型.基于随机车流荷载数据,考虑车-桥耦合振动影响,建立了新的拱桥吊杆疲劳分析模型.以某拱桥为工程背景,对比研究了拱桥不同因素作用下典型吊杆的疲劳损伤及疲劳寿命.
1 桥面退化模型的建立
1.1 桥面平整度标准
常用的桥面平整度功率谱函数如式(1)所示.[9]
Gd(n)=Gd(n0)×(n/n0)-w.
(1)
式中:n表示空间频率,m-1;n0表示参考空间频率,其值为0.1 m-1;Gd(n0)表示位移功率谱密度,m3;w表示频率系数,它决定了PSD的频率结构,一般取2.
位移功率谱密度与速度功率谱密度之间的转换关系为[9]:
Gv(n)=Gd(n)·(2πn)2.
(2)
式中:Gv(n)表示速度功率谱密度.
GB/T 7031—2005中的道路分级见表1.
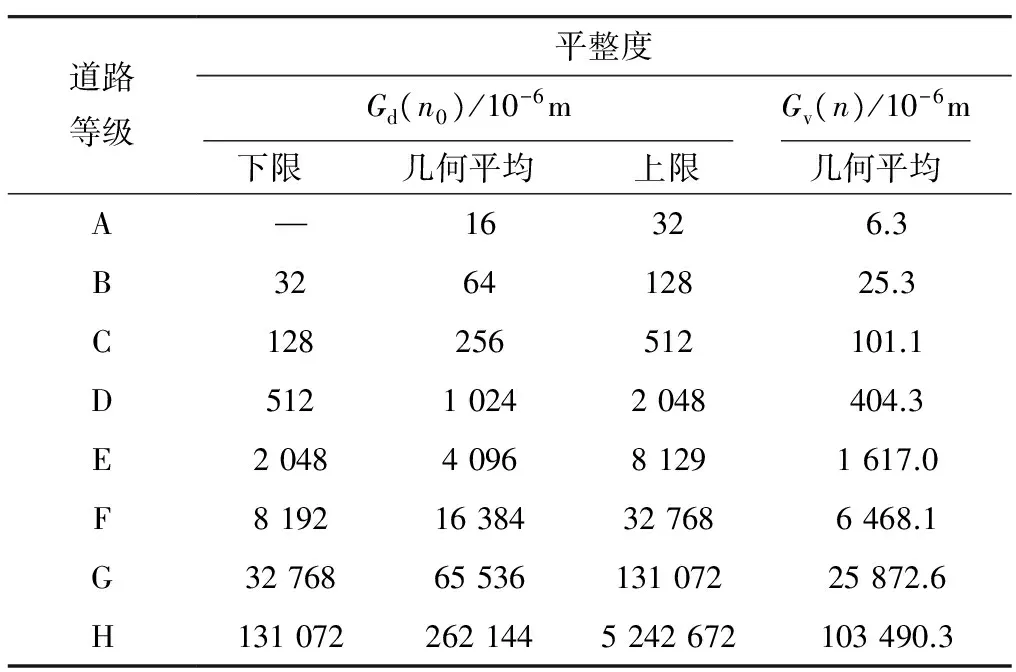
表1 GB/T 7031—2005道路分级
1.2 桥面退化理论模型
目前使用较多的桥面平整度为国际平整度指数IRI,桥面功率谱密度与国际平整度指数的关系式见式(3)[8].
(3)
由于ω=2πf=2πvn,可得如下关系:
(4)
式中:IRI为国际平整度指数;v为速度;ω为角频率;Hs(ω)为理论车辆模型中簧载质量的频率响应函数.
采用空间频率范围(0.02,2)对式(4)进行积分运算,可简化为式(5).
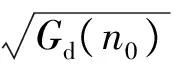
(5)
式中:a0为系数,取a0=103m-1.5.
不同等级桥面所对应不同国际平整度指数值见表2.
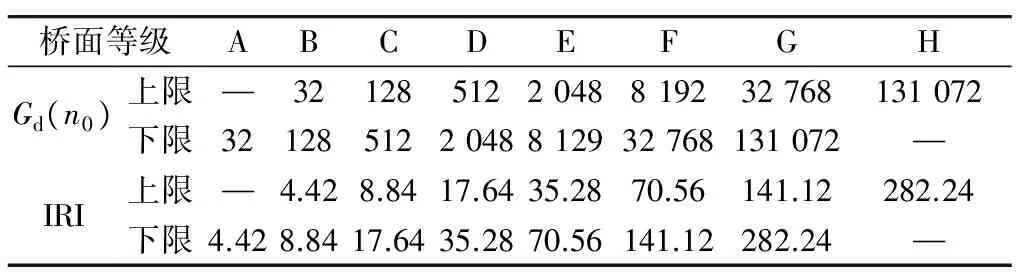
表2 不同IRI值范围与桥面等级对应表
国际平整度指数与运营时间的关系式如下:
IRIt=1.04eη t·IRI0+263(1+SNC)-5·
(CESAL)t.
(6)
式中:η为根据干湿状态与冻结条件确定的环境系数,取值范围为0.01~0.7;IRI0为桥面建造完成后,但未正式运营通车之前的初始国际平整度指数;t为桥梁运营时间,年;SNC为根据桥面各结构层厚度确定的结构系数;(CESAL)t为根据车流量情况随时间变化换算100 kN累计当量轴次,以百万次计.
综合以上各式可得桥面平整度系数随时间变化的计算式:
Gd(n0)=
(7)
2 建立桥梁模型
以某中承式拱桥为工程背景,分析其桥面平整度随运营时间增长的退化历程,以及桥面退化对吊杆疲劳分析的影响.拱桥主桥跨径530 m,设双向4个行车道及双侧人行道.桥梁设计荷载等级为公路荷载Ⅰ级.主桥的立面布置如图1所示.
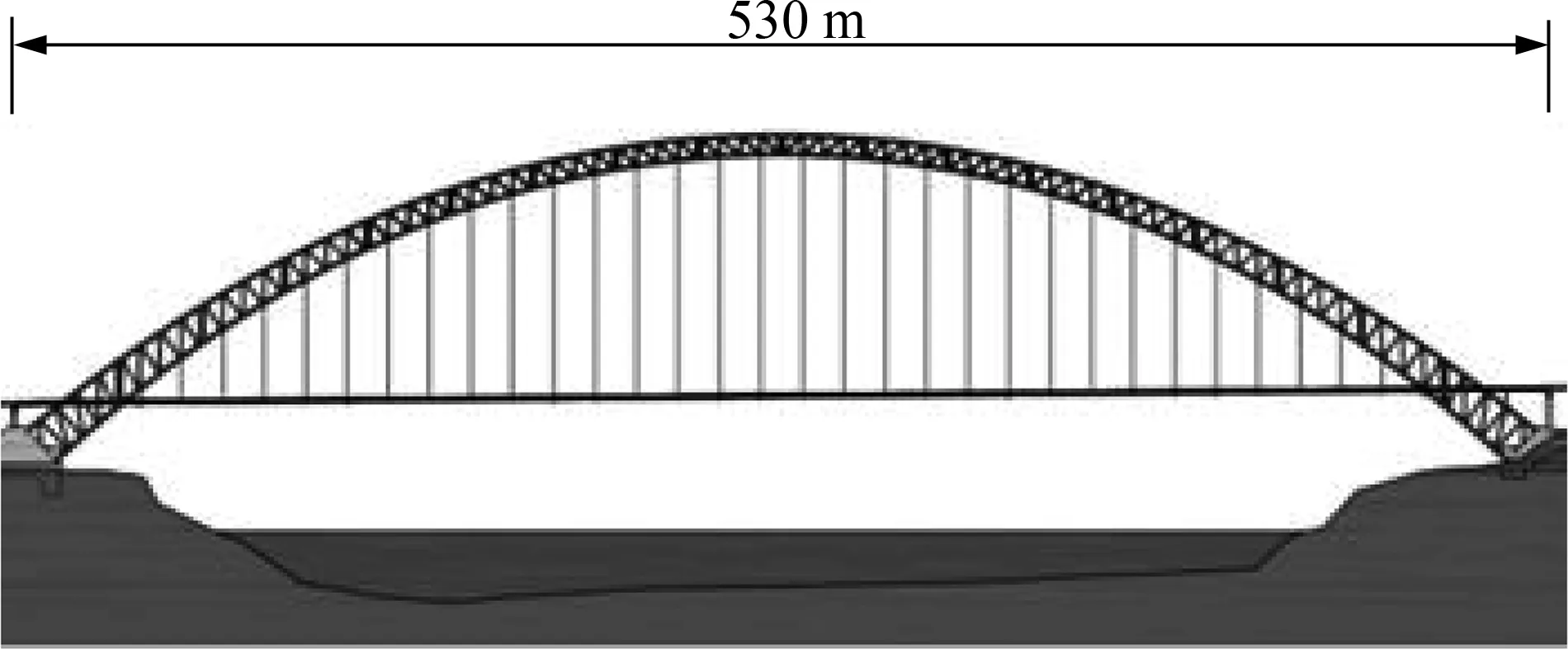
图1 拱桥主桥布置图
通过桥梁有限元方法建立拱桥数值模型,如图2所示.
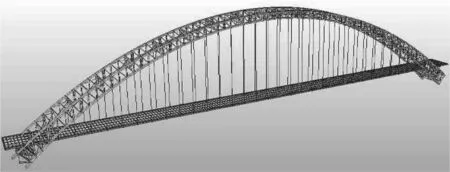
图2 桥梁有限元模型
选择端部两根短吊杆1#和2#,跨中两根长吊杆4#和5#,以及1/4跨处吊杆3#作为典型吊杆进行疲劳分析.如图3所示.
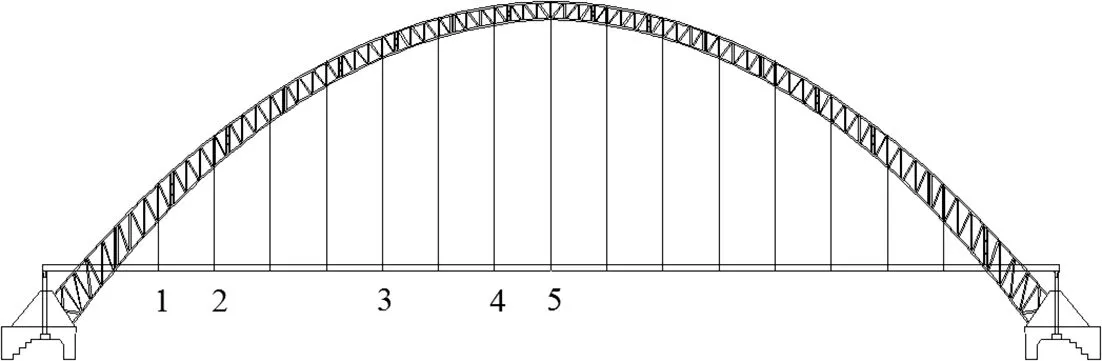
图3 桥梁典型吊杆
3 桥面平整度退化分析及模拟
3.1 桥面平整度退化分析
基于某拱桥的结构特征、气候环境条件、交通量、保养维护水平等各个因素,假定该桥梁最初桥面平整度等级为A级,桥面条件无退化,拟定式(6)中根据桥面各结构层厚度确定的结构系数SNC=4,根据干湿状态与冻结条件确定的环境系数η=0.2[8].根据该桥2014年某个工作日24 h(0:00—24:00)交通量实测数据,将年交通量平均增长率分为γ=0%、γ=3%、γ=5%三个等级进行对比分析.可预测某桥超车道和行车道未来15年内的桥面平整度系数和国际平整度指数,两者变化趋势分别如图4与图5所示.
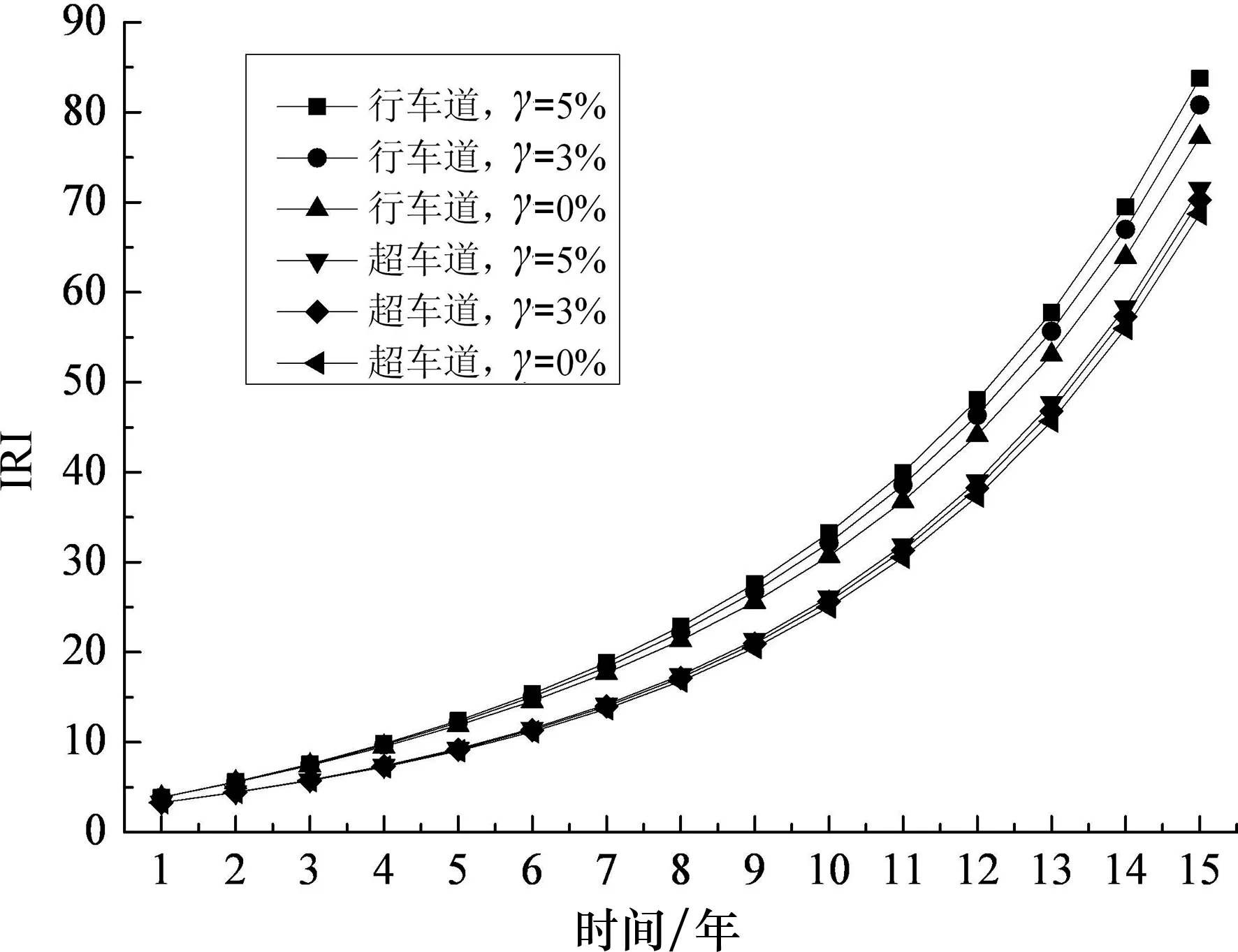
图4 国际平整度指数15年变化值
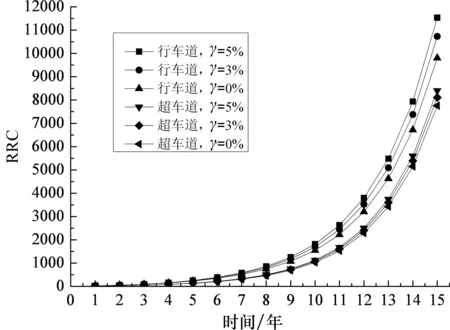
图5 桥面平整度系数15年变化值
由图4和图5可知,国际平整度指数和桥面平整度系数均呈非线性变化趋势,且随着时间增长,其变化速率越来越快,如交通量年增长率γ=5%时,超车道在第1~2年桥面等级为A级,第3~4年桥面等级为B级,第5~8年桥面等级为C级,第9~11年桥面等级为D级,第12~14年桥面等级为E级,第15年桥面等级为F级.而行车道在第1年桥面等级为A级,第2~3年桥面等级为B级,第4~6年桥面等级为C级,第7~9年桥面等级为D级,第10~14年桥面等级为E级,第15年桥面等级为F级.
3.2 桥面平整度退化模拟
用三角级数法进行桥面平整度模型的模拟,桥面平整度函数如式(8)所示[8-9].
(8)
式中:Gd(n)=Gd(n0)t·(n/n0)-2,有效频率上限和下限分别为nd=0.2 m-1和nu=2 m-1,参考频率nd=0.1 m-1,φi为0~2π之间均匀分布的随机数.桥面平整度系数也可通过图4和图5得到.图6所示为交通量年平均增长率γ=0%时,拱桥超车道桥面平整度样本曲线图.
如图6所示,桥面平整度波动程度更加剧烈,波峰和波谷的峰值也越来越大.交通量年平均增长率γ=0%的情况下,超车道第1年的竖向峰值为1.234 cm,第5年竖向峰值为4.849 cm,第10年竖向峰值为8.126 cm,第15年竖向峰值为13.839 cm.
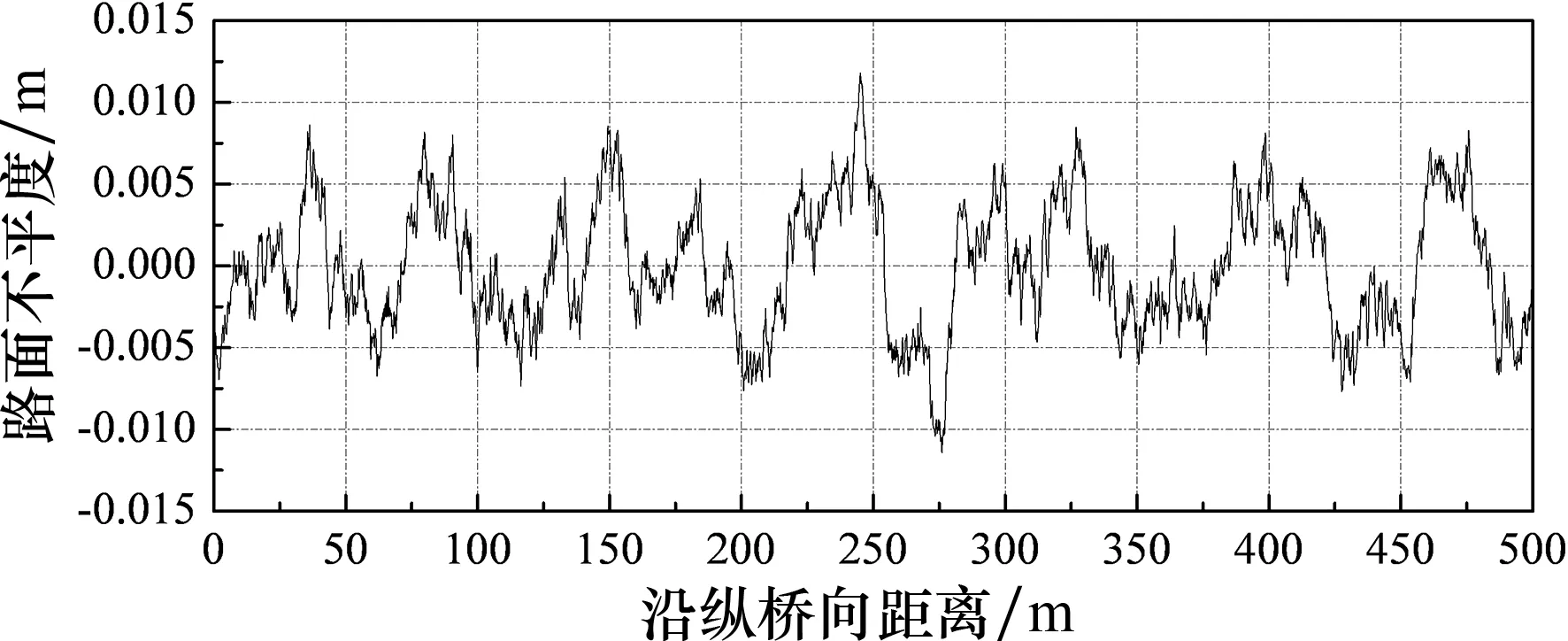
(a) 第1年桥梁桥面平整度样本
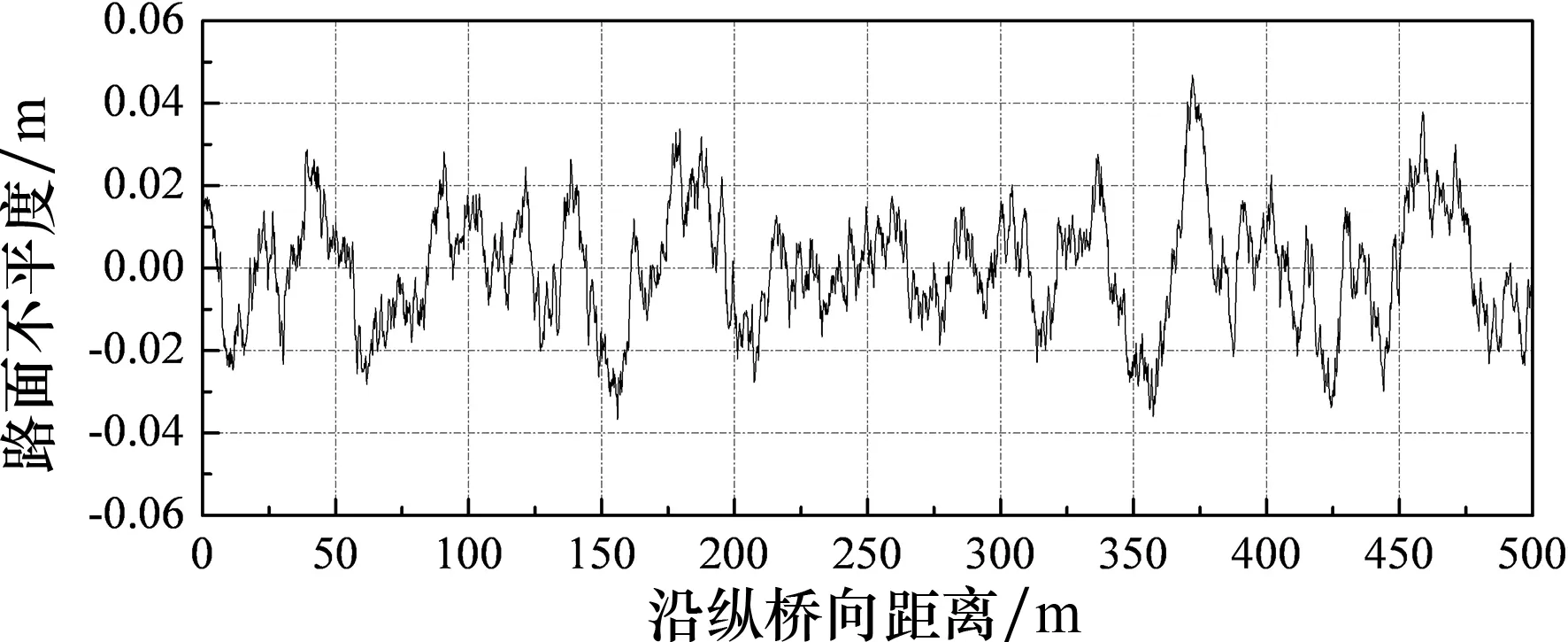
(b) 第5年桥梁桥面平整度样本
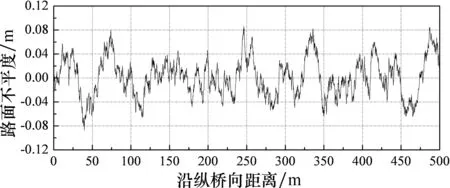
(c) 第10年桥梁桥面平整度样本
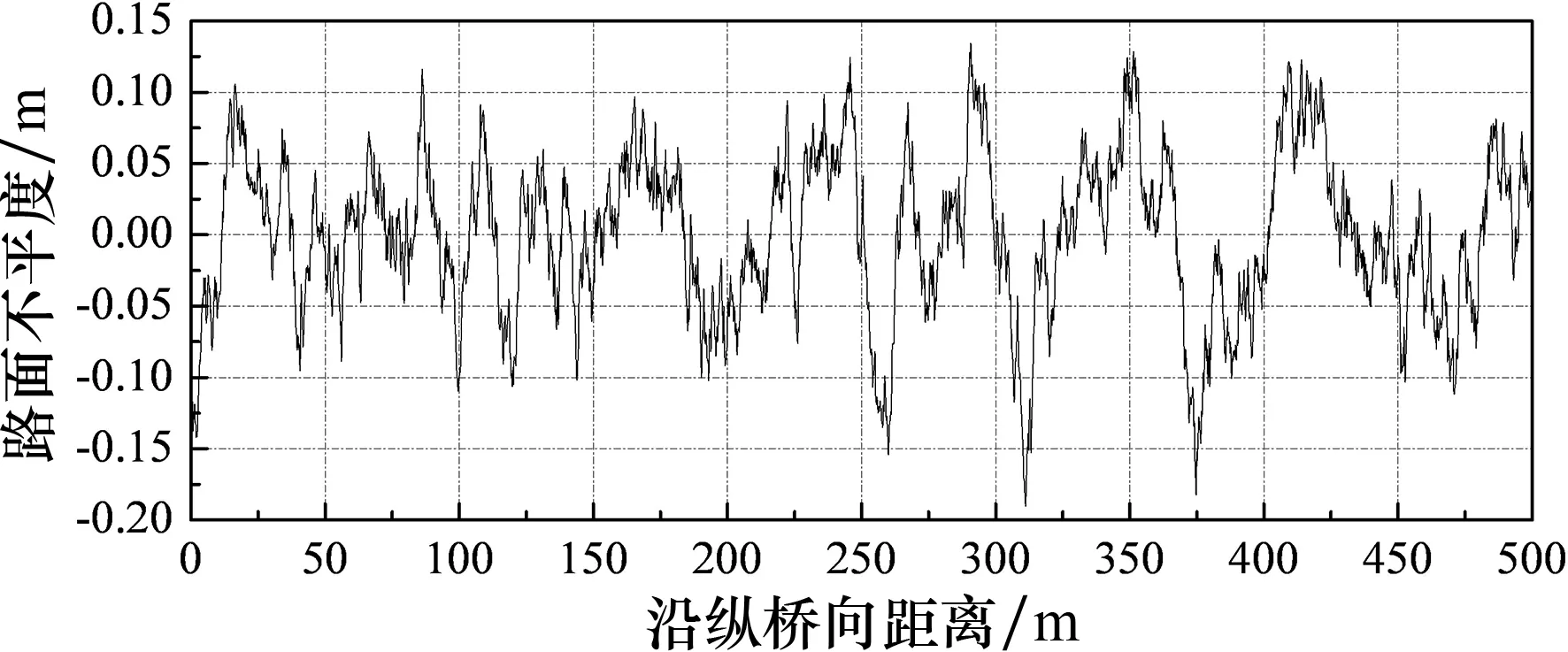
(d) 第15年桥梁桥面平整度样本 图6 桥梁桥面平整度样本曲线
4 随机车流模型
以某拱桥2014年某个工作日24 h(0:00—24:00)车流实测数据为基础来建立随机车流模型.通过交通调查得到的样本数量为15 266辆,通过查阅当地交通管理部门的资料可知,该桥该月平均日交通量为16 000辆,两者相对差值为4.8%.将公路桥梁车辆简化为5类典型车辆模型.典型车通行量、轴重及轴距等具体参数见表3.
根据蒙特卡洛原理,车型、车道位置、车辆间距、车重等都是相互独立的随机值.根据统计研究可知,车道参数服从均值分布,车型参数服从均值分布,车重服从极值Ⅰ型分布,车间距服从对数正态分布[11-12].通过对某桥的24 h车流数据的统计以及随机车流代表车型的分类,可知,车型参数从V1至V5所占(0,1)区间的比例分别为0.740、0.213、0.013、0.031、0.003,通过均匀分布随机抽样产生.车重服从极值Ⅰ型分布,各类车型平均车重和车重标准差见表4.
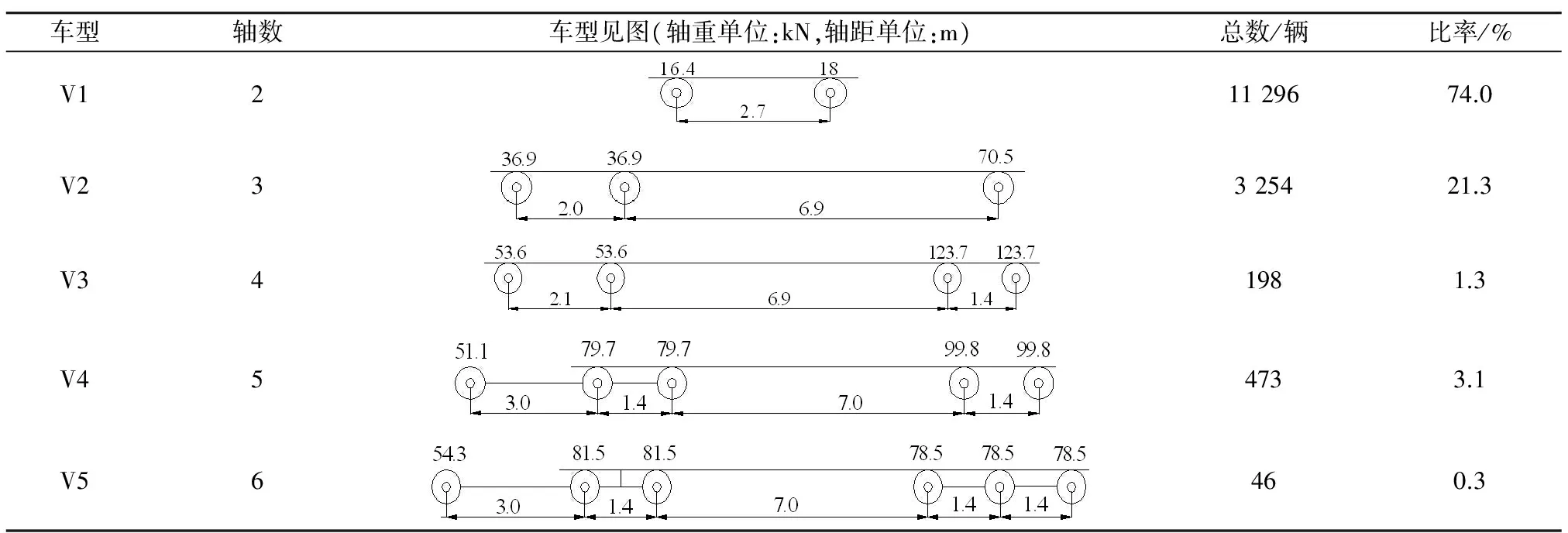
表3 五类模型车辆荷载频值谱
表4车重和轴重标准差
Tab.4Theweightstandarddeviationofvehicleandaxle
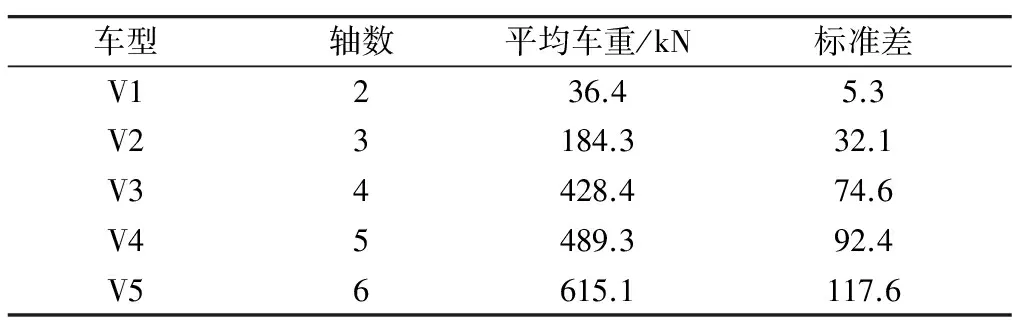
车型轴数平均车重/kN标准差V1236.45.3V23184.332.1V34428.474.6V45489.392.4V56615.1117.6
通过各车型车重标准差可求得随机车重,车道分布参数的求解与车型分布相似,由于某桥模型为双向4车道模型,车道分布参数在超车道和行车道所占(0,1)区间的比例分别为0.3和0.7,通过均匀分布随机抽样产生.车辆间距参数服从对数正态分布,根据车型轴重比例可求得随机轴重.本文随机车流模型中车辆车间距参数均值及标准差分别为4.8 m、1.1 m.将车速划分为40 km/h、60 km/h、80 km/h、100 km/h、120 km/h,车速也可通过均匀分布随机抽样产生.
5 吊杆疲劳分析
5.1 恒载作用下吊杆内力
由于拱桥横向结构对称,上下游吊杆受力基本一致,且达到60根.故只列出一侧拱肋上吊杆的恒载作用下内力图,如图7所示.
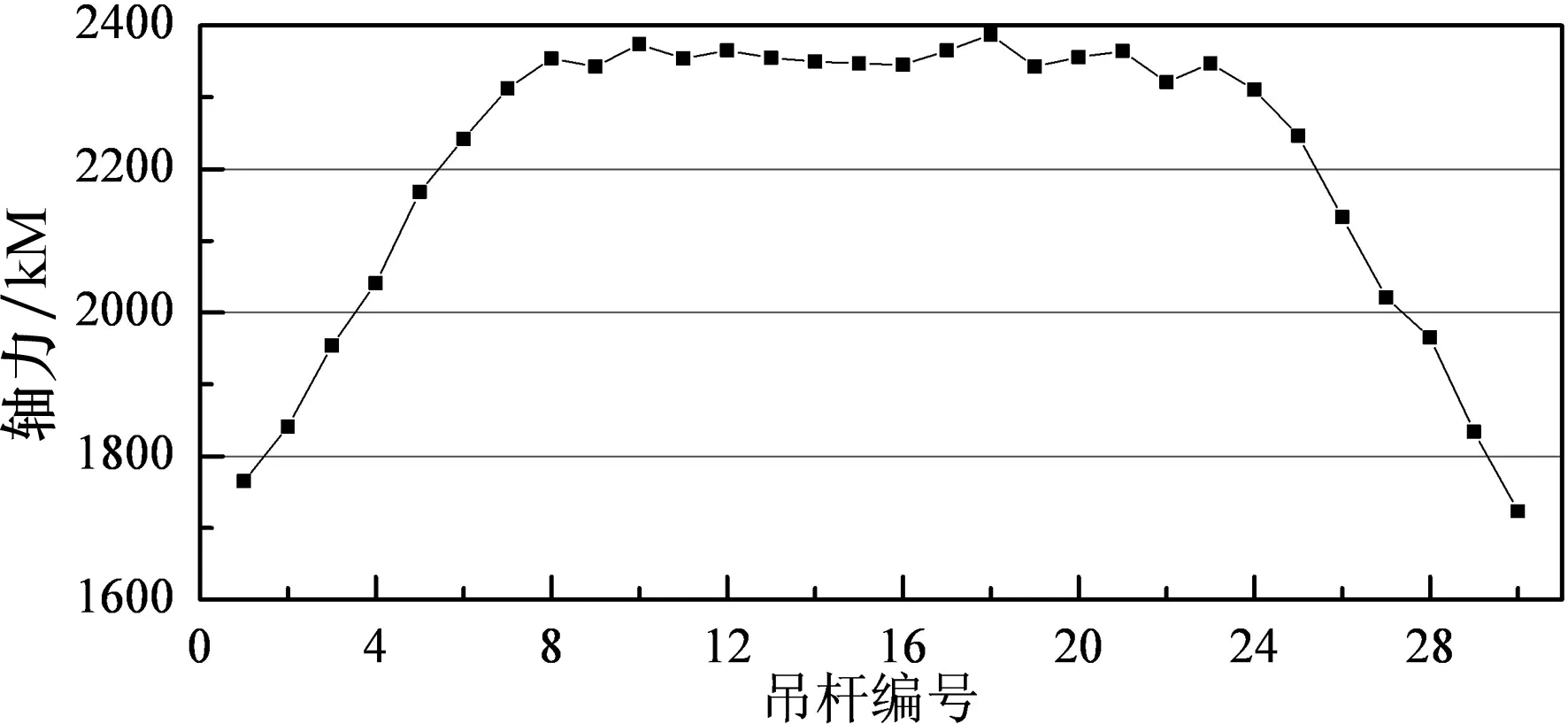
图7 恒载作用下吊杆轴力图
从图7可知,在恒载作用下吊杆的轴力由靠近端部的1号吊杆1 787 kN逐步上升至8号吊杆的2 375 kN,从8号吊杆至23号吊杆轴力平稳无波动,从23至30号吊杆轴力逐渐降低至1 754 kN.总体来说两侧的短吊杆轴力值小于其他吊杆轴力值,中间吊杆内力基本一致,与试验所测吊杆轴力分布规律一致.
5.2 单车作用下吊杆应力曲线
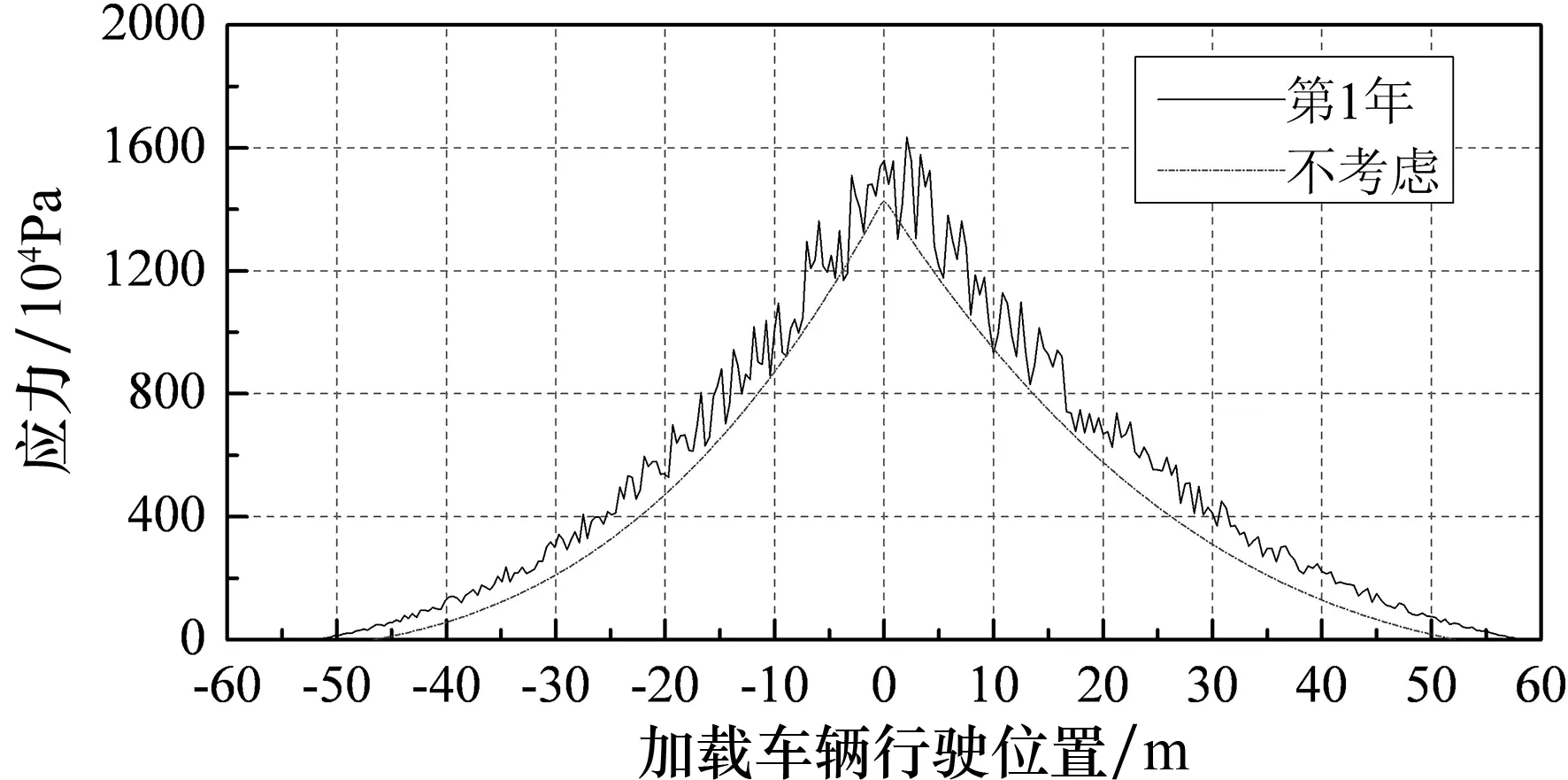
车辆加载时,忽略恒载对分析结果的影响,假设恒载作用吊杆应力为初始值零.限于篇幅仅列出两轴标准车辆以相同速度通过桥面平整度等级为A~F级时各个典型吊杆的应力历程.如图8和图9所示,图中分别为V1标准车辆以80 km/h的速度通过桥面平整度等级为A级(第1年)、C级(第5年)、D级(第10年)及F级(第15年)桥面时,1#和5#典型吊杆的应力历程.图中虚线表示不考虑桥面平整度等级及车桥耦合的情况下车辆通过桥梁时应力曲线;图8和图9中实线部分则表示在考虑桥面平整度等级及车桥耦合振动的情况下吊杆的应力曲线.
(a)A级桥面
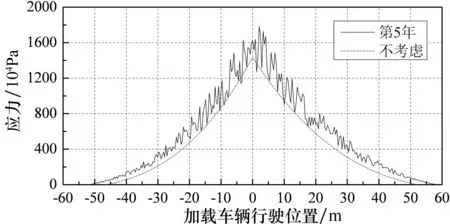
(b) C级桥面
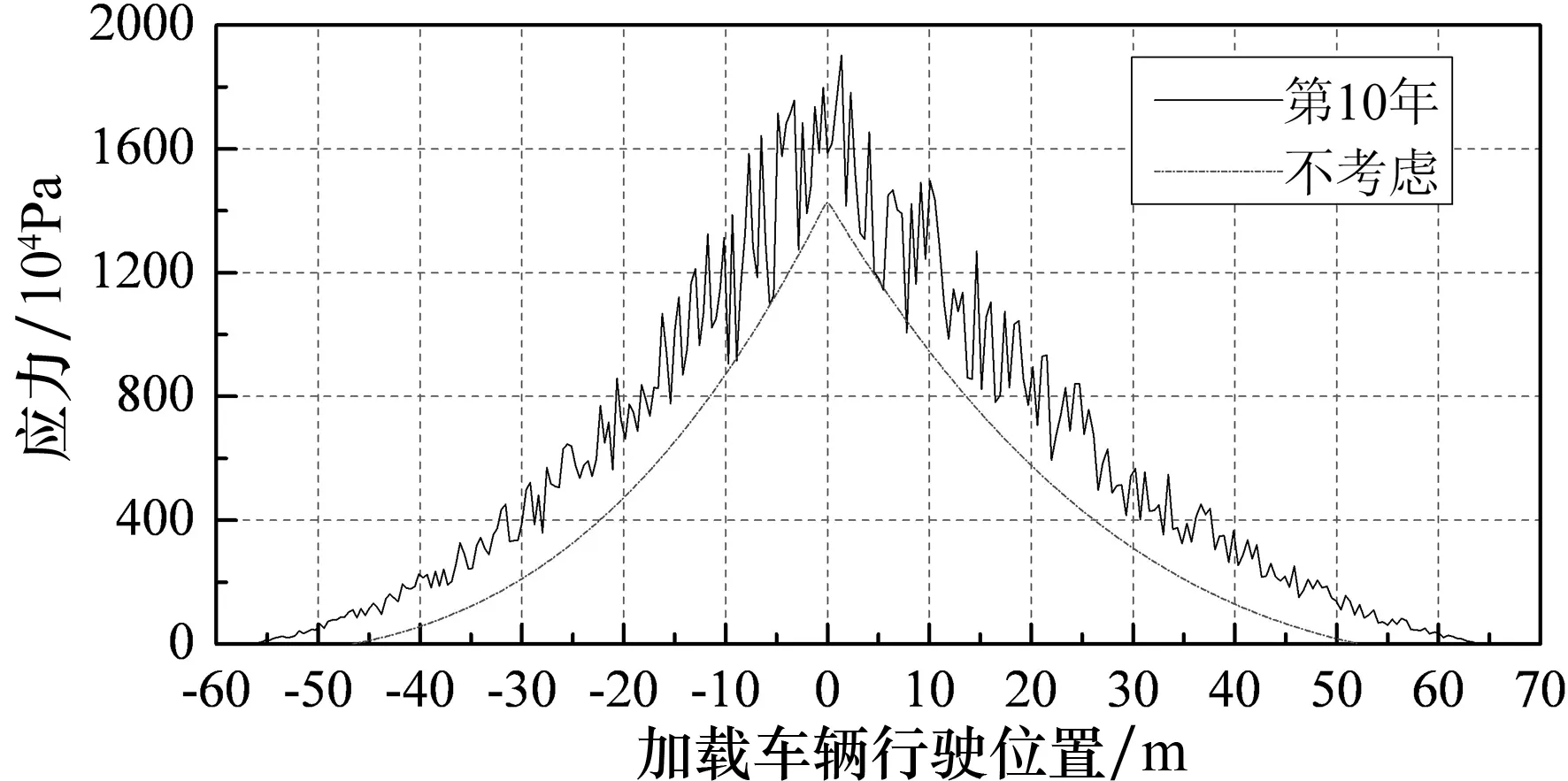
(c)D级桥面
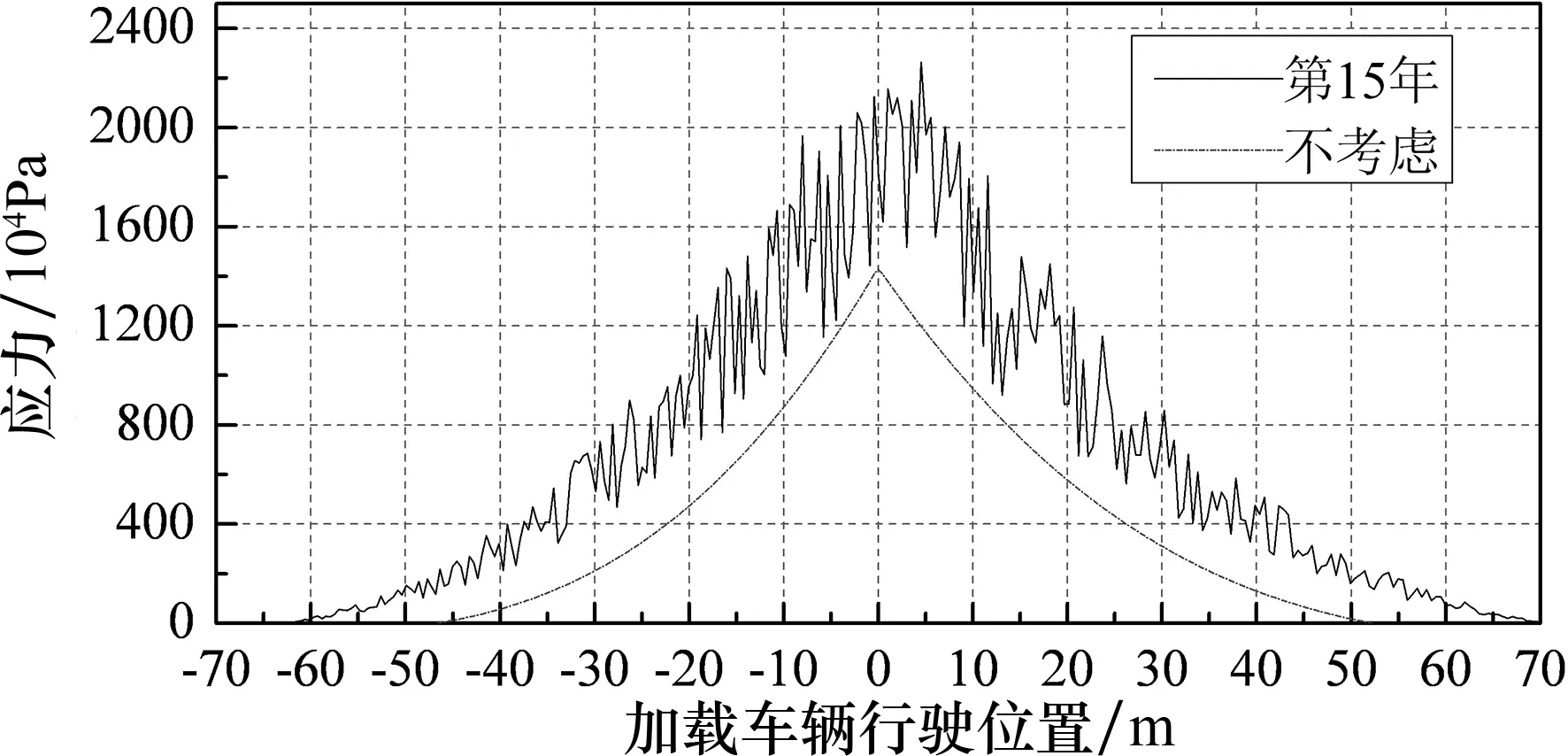
(d)F级桥面 图8 V1(80 km/h )单车作用下1#吊杆应力曲线
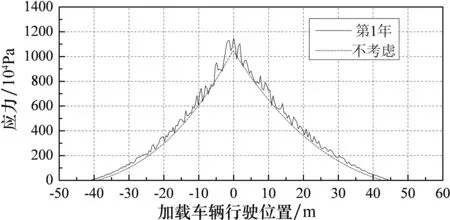
(a)A级桥面
(b) C级桥面
(c) D级桥面
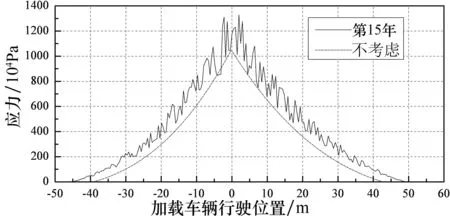
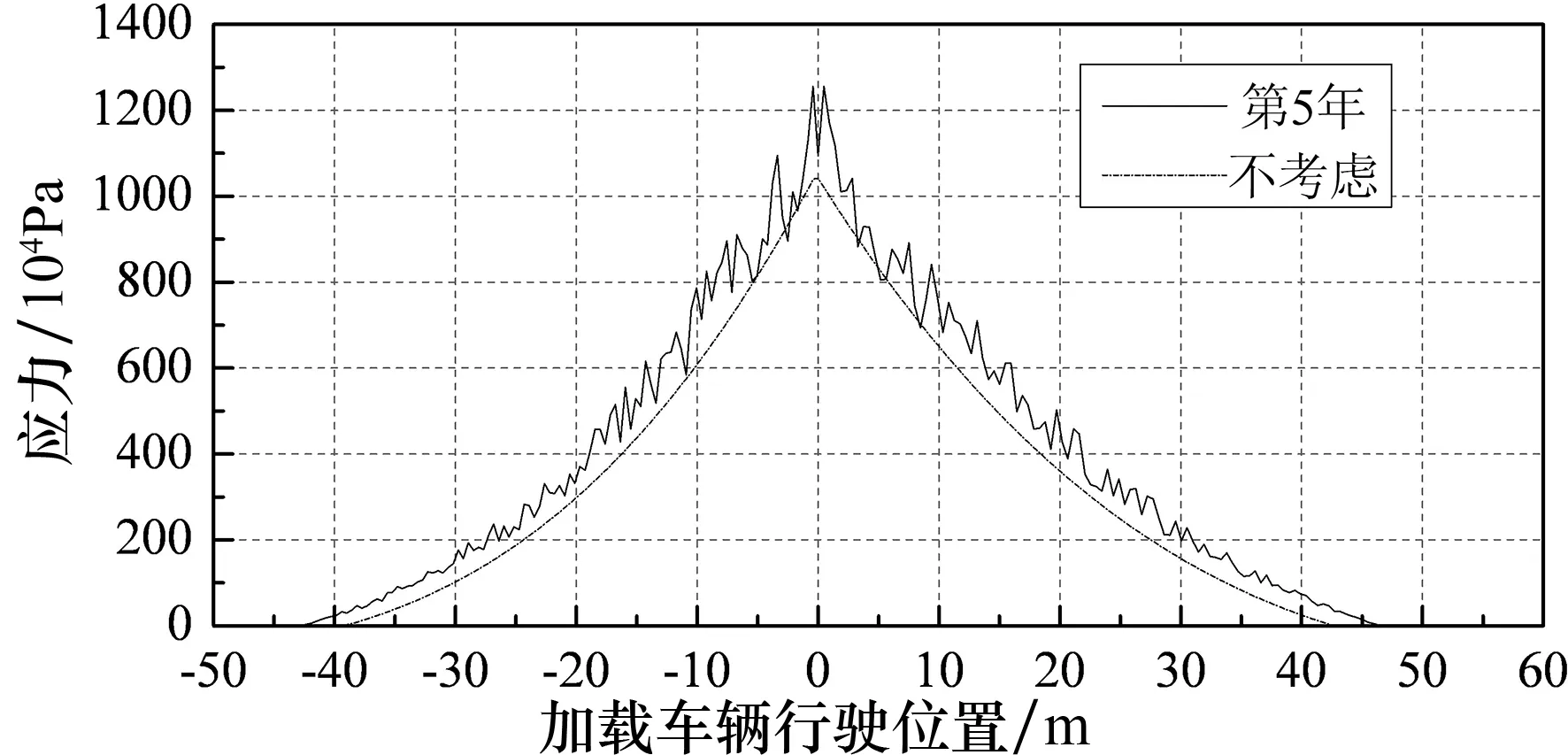
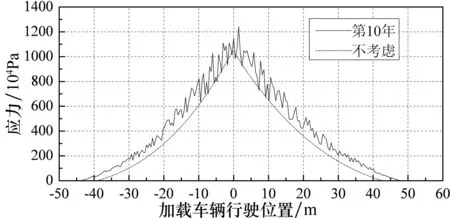
(d) F级桥面 图9 V1(80 km/h )单车作用下5#吊杆应力曲线
由图8和图9可知,在疲劳荷载作用下,靠近端部短吊杆比中部吊杆应力幅值更大,振动更加剧烈,在设计过程中应给予足够的重视.
同时,桥面平整度等级对吊杆应力曲线存在一定影响.桥面越不平整,吊杆的应力极值越大,吊杆应力曲线的波动也随着桥面状况变差而更加剧烈,出现正应力的范围也在增大.如不考虑桥面平整度等级时1#吊杆的应力幅值最大为14.2 MPa;考虑桥面平整度(桥面等级为F级)时,吊杆最大应力幅值为22.1 MPa,是前者的1.55倍.吊杆应力曲线的波动幅度随着桥面状况变差而逐渐变大.
5.3 随机车流作用下吊杆应力历程分析
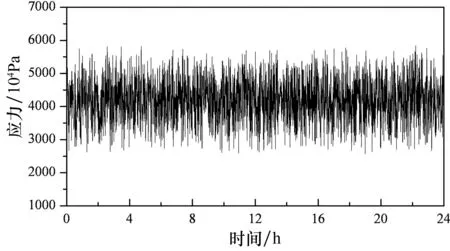
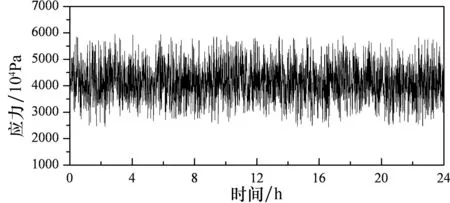
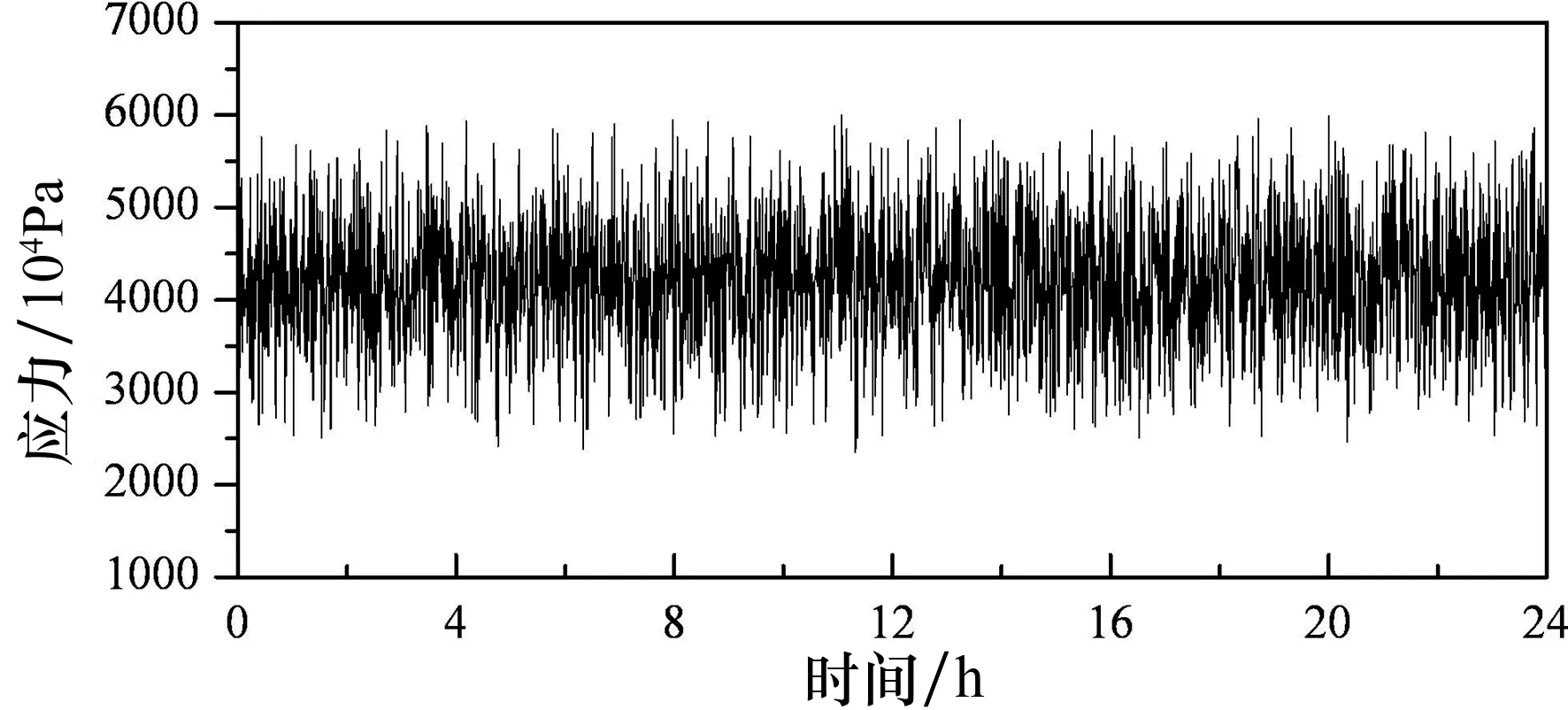
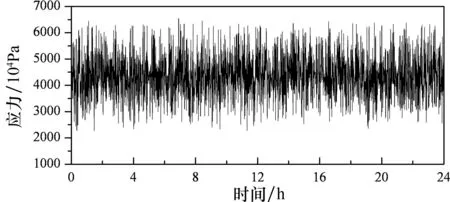
基于已编制随机车流-桥梁耦合计算程序[8-9],获得随机车流通过不同平整度等级桥面时典型吊杆24 h的应力时程曲线,对比分析随机车流荷载下桥面退化对吊杆应力时程的影响.图10为随机车流通过桥面平整度等级为B~F级桥面时1#吊杆的24 h应力时程曲线.
(a)B级桥面
(b)C级桥面
(c)D级桥面
(d)E级桥面
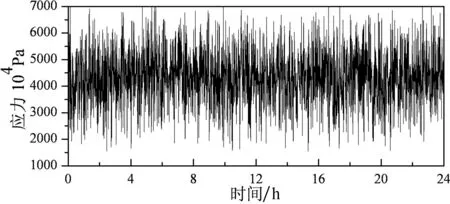
(e)F级桥面 图10 随机车流作用下1#吊杆应力时程曲线
由图10可知,不同桥面平整度等级对吊杆应力时程曲线的影响不仅体现在单车荷载中,随机车流荷载作用下吊杆的应力幅值和应力历程波动剧烈程度也随着桥面状况的退化而逐渐增大,这将影响到拱桥吊杆正常使用过程中疲劳分析结果.
5.4 吊杆疲劳损伤计算
交通量的增长对吊杆疲劳寿命的影响不仅在于荷载车辆的增加使吊杆承担更大工作负荷,而且会加速桥面退化,强化车辆-桥梁耦合振动激励.因此对于交通量增长因素的研究不能片面进行,应综合考虑.
为全面分析车-桥耦合系统中桥面退化、交通量增长等参数对在役拱桥吊杆的疲劳寿命分析的影响,将是否考虑桥面退化及交通量增长率两因素作为主要参数,将模型分为6种计算模型,具体见表5,其中初始桥梁桥面平整度等级为A级.图11所示为不同模型条件下典型吊杆在不同服役时间的年疲劳损伤.

表5 各模型参数
如图11所示,吊杆在桥面等级退化因素和交通量增加因素单独或共同作用下,早期疲劳损伤发展较慢,随着时间的增长,年疲劳损伤发展也会加快,这也许是由于交通量和桥面退化因素都是以时间为横轴的增长函数,运营时间越长,对吊杆疲劳损伤的影响越明显.以1#吊杆为例,第1年的年疲劳损伤值为8.326×10-3,若不考虑交通量的增长只考虑桥面退化因素,则第15年1#吊杆的年疲劳损伤值为12.443×10-3(见模型2);若只虑交通量的增长不考虑桥面退化因素,则交通量年平均增长率为γ=5%的情况下,第15年1#吊杆的年疲劳损伤值为13.526×10-3(见模型5);若交通量的增长和桥面退化因素共同考虑,则交通量年平均增长率为γ=5%的情况下,第15年F级桥面等级条件吊杆的年疲劳损伤值为15.156×10-3(见模型6).由上可知在不考虑桥面退化等因素时算出的吊杆疲劳损伤值偏小.
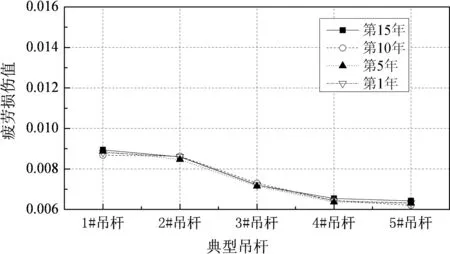
(a)模型1
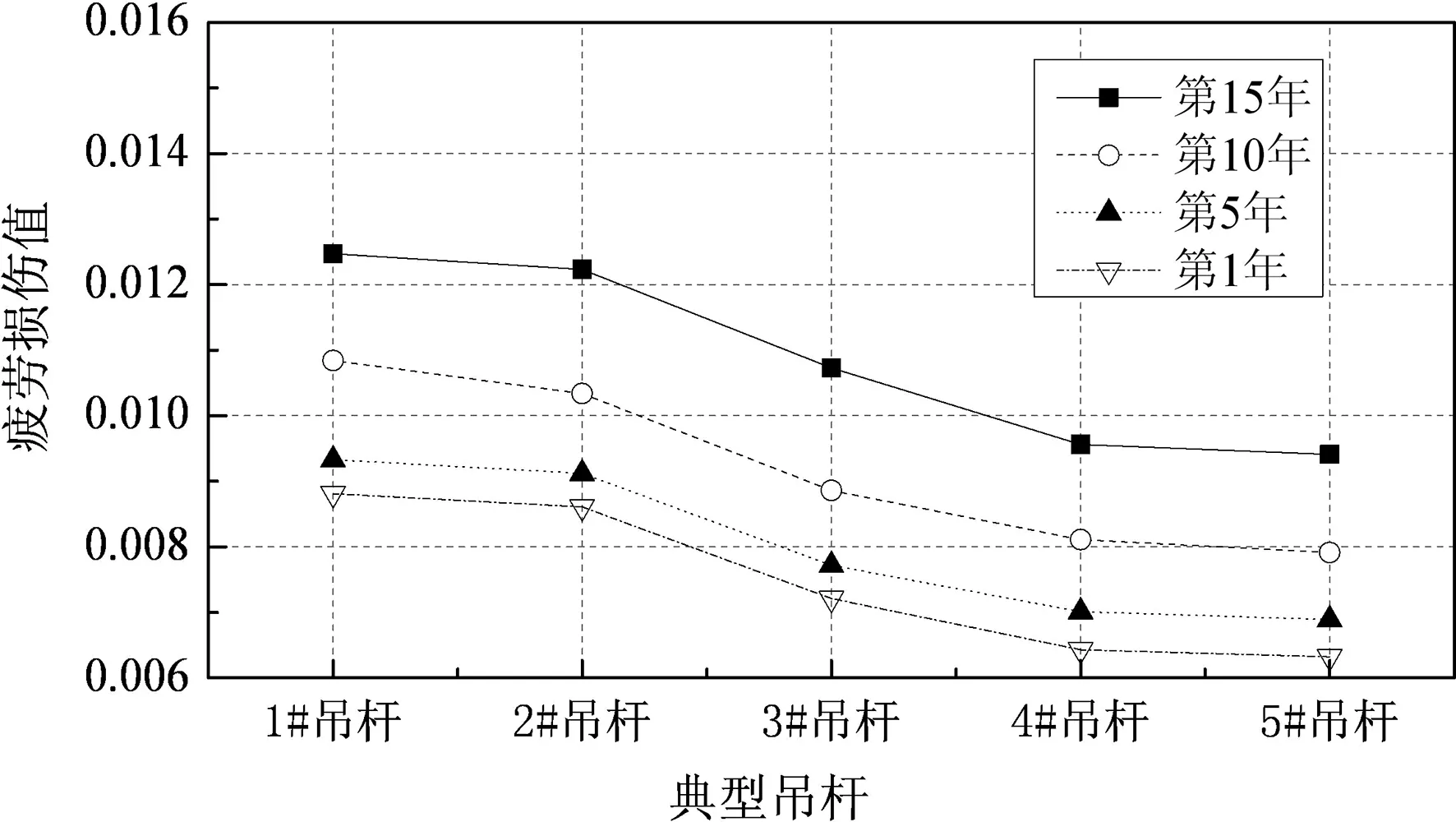
(b)模型2
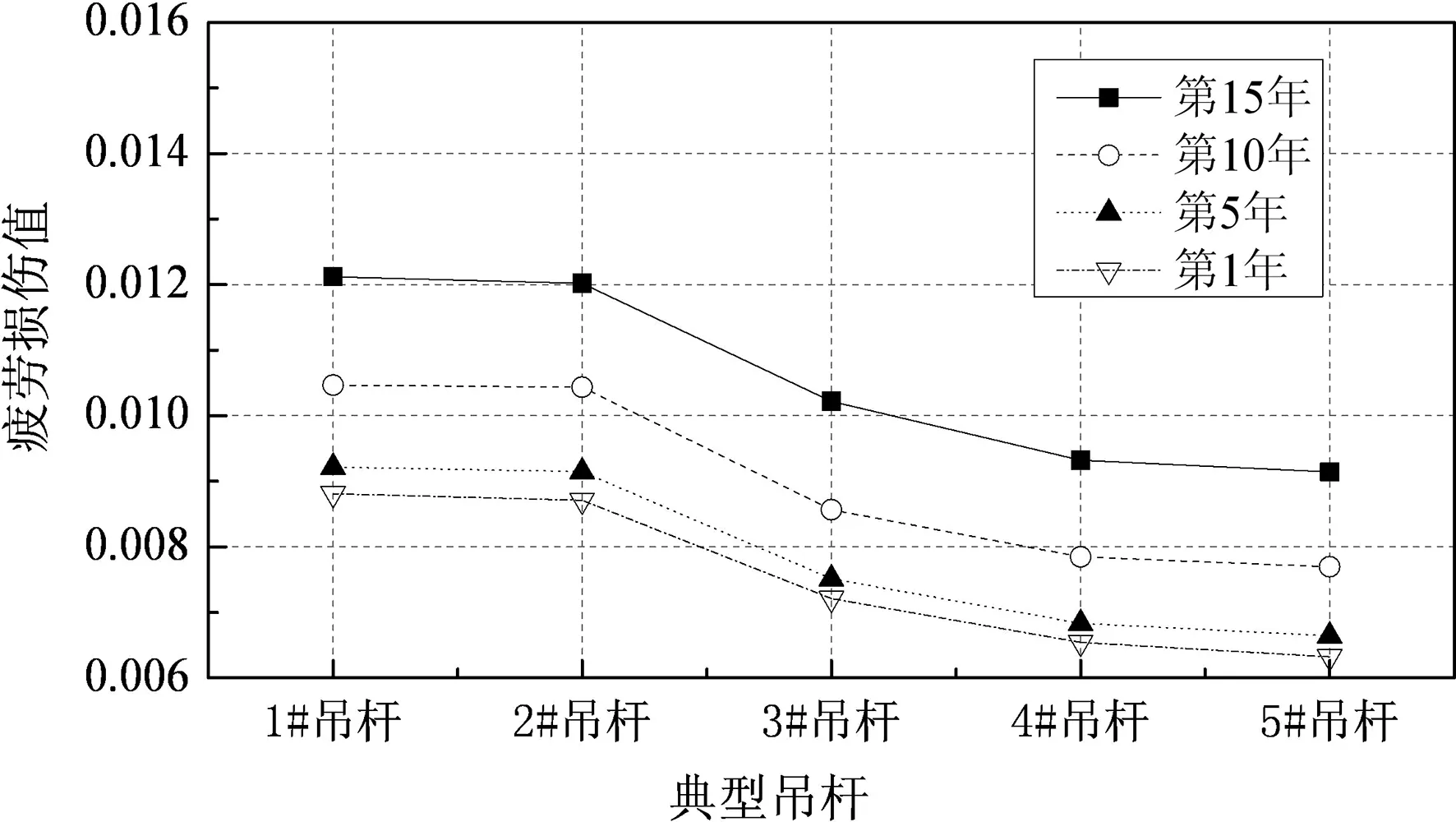
(c)模型3
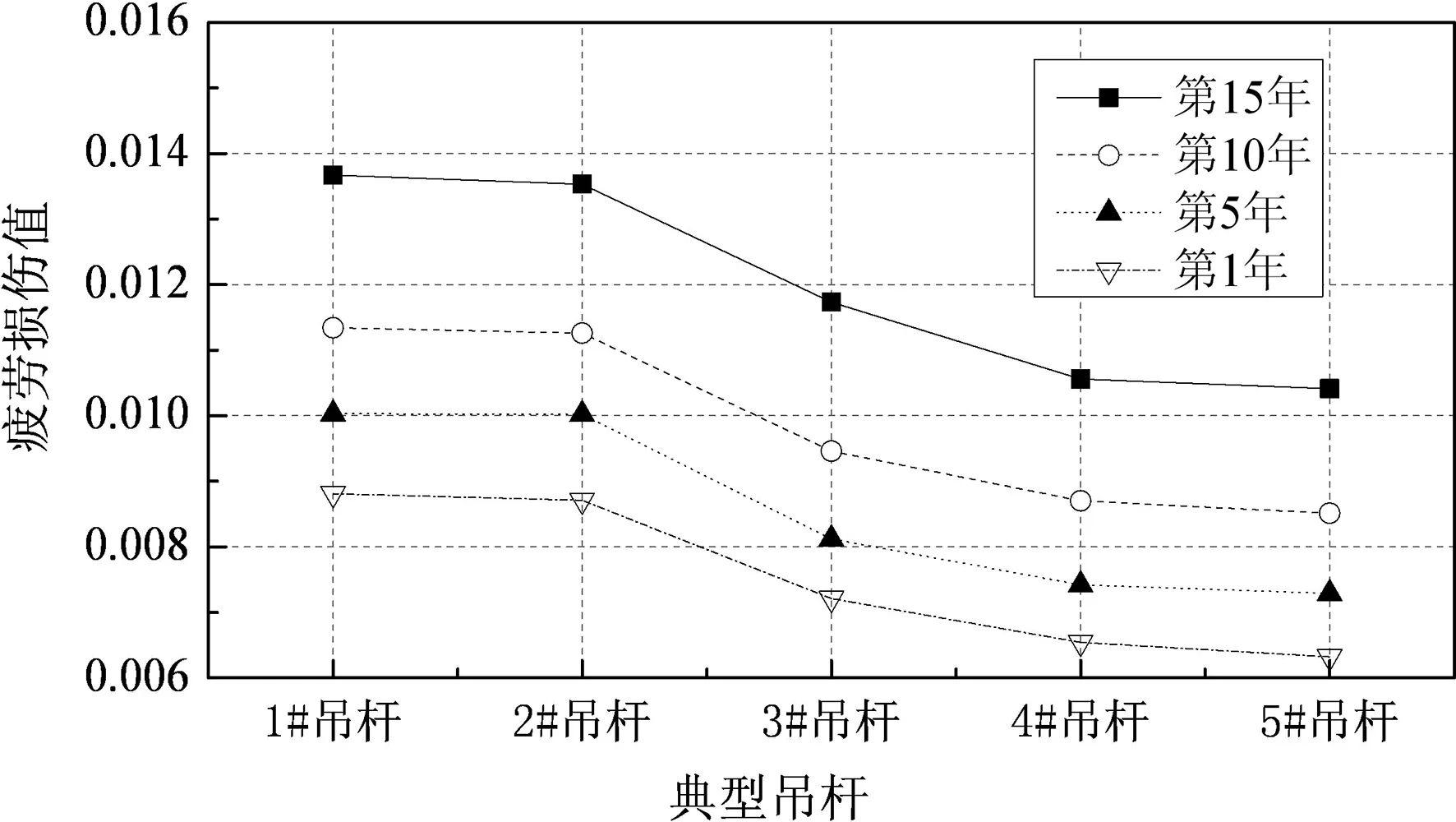
(d)模型4
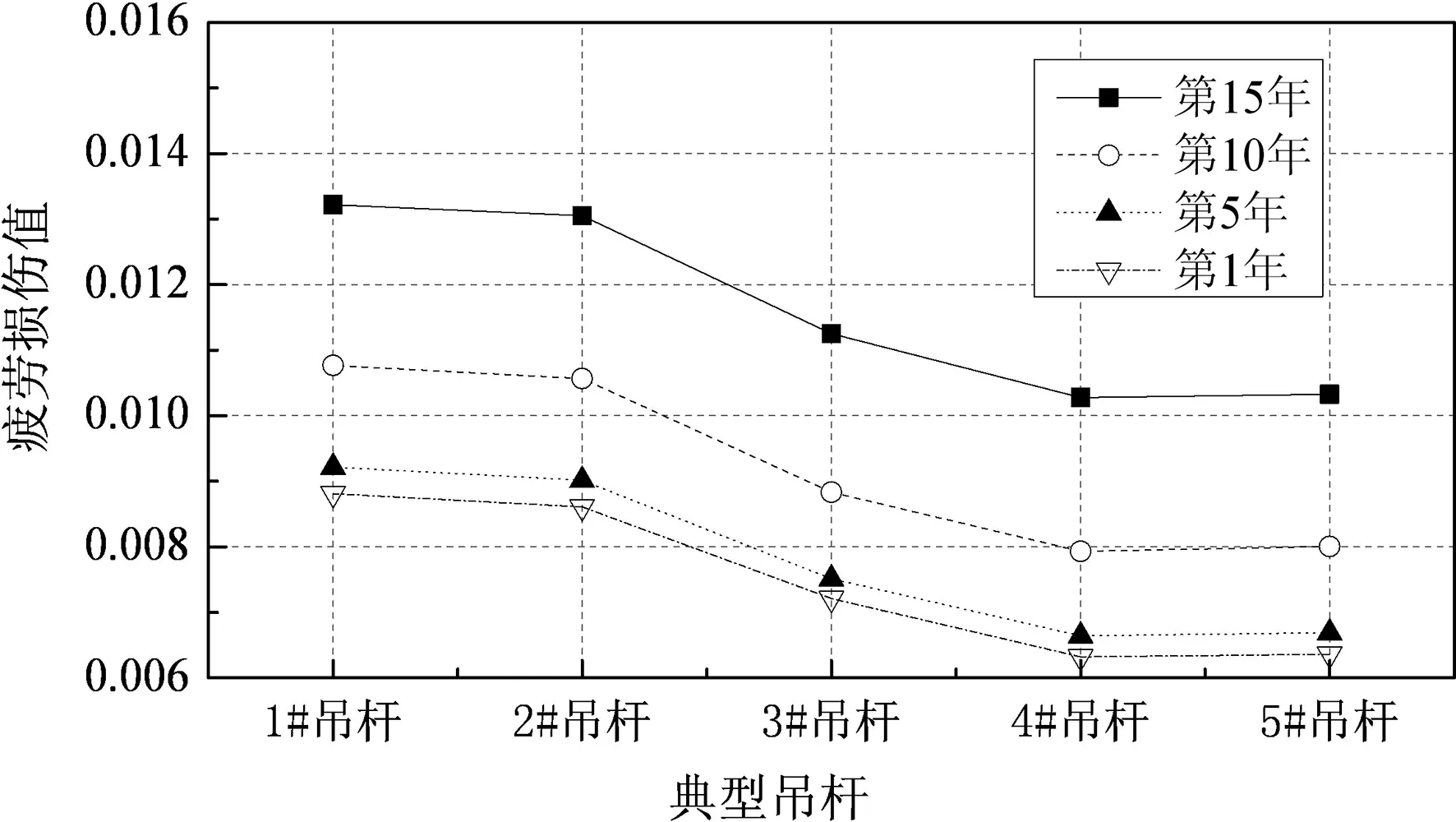
(e) 模型5
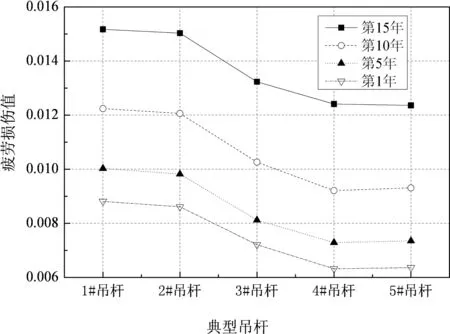
(f)模型6 图11 各模型典型吊杆年疲劳损伤
由模型6可求得考虑交通量增长、桥面退化条件下各吊杆的疲劳寿命,拱桥上下游各边除端部8根短吊杆疲劳寿命少于设计基准期,其余各吊杆疲劳寿命皆超过设计基准期.对比发现,考虑车-桥耦合及桥面退化共同影响下,计算得到的吊杆疲劳寿命值比不考虑两者影响所得值少15~30年.具体如图12所示.
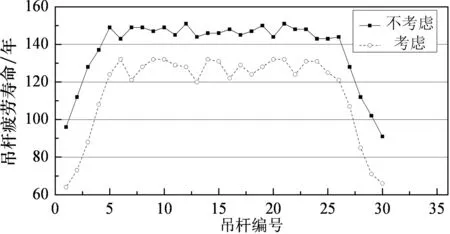
图12 各吊杆疲劳寿命图
6 结 论
本文根据在役桥面平整度等级国际通用评价体系,模拟了运营阶段桥面平整度退化历程.结合已编制随机车流-桥梁耦合振动分析程序,建立了可考虑车-桥耦合振动及考虑桥面退化等因素的拱桥吊杆疲劳分析模型.以某拱桥为工程背景,对比研究了不同因素作用下拱桥典型吊杆的疲劳损伤及疲劳寿命.结论如下:
1)在疲劳荷载作用下,不论是否考虑车-桥耦合及桥面等级退化等因素,靠近端部短吊杆比中部吊杆应力幅值更大且振动更加剧烈,也对桥面等级退化因素的反应更加敏感,在设计过程中应给予足够的重视.
2)考虑车-桥耦合振动及桥面退化影响的拱桥吊杆疲劳计算模型的分析结果更加精确.考虑车-桥耦合及桥面退化共同影响下,计算得到的吊杆疲劳寿命值比不考虑两者影响所得值少15~30年.
3)桥面平整度等级对吊杆应力历程存在一定影响.吊杆应力曲线的波动及应力幅值均随着桥面状况变差而更加剧烈,且出现正应力的范围也在增大.如不考虑桥面平整度等级时1#吊杆的应力幅值最大为14.2 MPa;考虑桥面平整度(桥面等级为F级)时,吊杆最大应力幅值为22.1 MPa,是前者的1.55倍.
[1] 夏禾.车辆与结构动力相互作用[M].北京:科学出版社,2005:154-164.
XIA He.Vehicle structure interaction[M].Beijing:Science Press,2005:154-164.(In Chinese)
[2] YIN X F,FANG Z,CAI C S.Lateral vibration of high-pier bridges under moving vehicular loads[J].Journal of Bridge Engineering,2011,16(3):400-412.
[3] DENG L,CAI C S.Bridge model updating using response surface method and genetic algorithm[J].Journal of Bridge Engineering,2010,15(5):553-564.
[4] 曾勇,陈艾荣,谭红梅.基于实测车流的悬索桥吊杆钢丝寿命期内的疲劳评定[J].防灾减灾工程学报,2014,34(2):185-191.
ZENG Yong,CHEN Airong,TAN Hongmei.Fatigue assessment of hanger suspension bridges in operation life based on in-situ traffic flow[J].Journal of Disaster Prevention and Mitigation Engineering,2014,34(2):185-191.(In Chinese)
[5] 李岩,吕大刚,盛洪飞.考虑随机车载-风载联合作用的斜拉桥拉索疲劳可靠性分析[J].中国公路学报,2012,25(2):60-66.
LI Yan,LÜ Dagang,SHENG Hongfei.Fatigue reliability analysis on cable of cable-stayed bridge under random vehicle load and wind load[J].China Journal of Highway and Transport,2012,25(2):60-66.(In Chinese)
[6] CHEN S R,CAI C S.Equivalent wheel load approach for slender cable-stayed bridge fatigue assessment under traffic and wind:feasibility study[J].Journal of Bridge Engineering,2007,12(6):55-64.
[7] ZHANG W,CAI C S.Fatigue reliability assessment for existing bridges considering vehicle speed and road surface conditions[J].Journal of Bridge Engineering,2012,17(3):443-453.
[8] 殷新锋,邓露.随机车流作用下桥梁冲击系数分析[J].湖南大学学报:自然科学版,2015,42(9):68-75.
YIN Xinfeng,DENG Lu.Impact factory analysis of bridge under random traffic loads[J].Journal of Hunan University:Natural Sciences,2015,42(9):68-75.(In Chinese)
[9] 殷新锋,丰锦铭,刘扬.考虑桥面等级退化影响的风-车流-桥梁耦合振动分析[J].工程力学,2016,33(3):87-94.
YIN Xinfeng,FENG Jinming,LIU Yang.Vibration of the bridge-traffic-wind system considering road surface progressive deterioration[J].Journal of Engineering Mechanics,2016,33(3):87-94.(In Chinese)
[10] 方志,向宇,匡镇,等.钢纤维含量对活性粉末混凝土抗疲劳性能的影响[J].湖南大学学报:自然科学版,2011,38(6):6-12.
FANG Zhi,XIANG Yu,KUANG Zhen,etal.Fatigue properties of reactive powder concrete with different steel fiber ratios[J].Journal of Hunan University:Natural Sciences,2011,38(6):6-12.(In Chinese)
[11] 卿宏军,韩旭,陈志夫,等.某轿车结构载荷谱采集与分析[J].湖南大学学报:自然科学版,2012,39(12):32-36.
QING Hongjun,HAN Xu,CHEN Zhifu,etal.Acquisition and analysis of loading spectral of a car structure[J].Journal of Hunan University:Natural Sciences,2012,39(12):32-36.(In Chinese)
[12] ZHOU Y F,CHEN S R.Dynamic simulation of a long-span bridge-traffic system subjected to combined service and extreme loads[J].Journal of Structural Engineering,2015,121(9):546-554.
Fatigue Analysis for Suspenders of Arch Bridge Addressing Vehicle-bridge Coupled Vibration and Road Surface Progressive Deterioration
YIN Xinfeng†,FENG Jinming,LIU Yang,CAI Chunsheng
(Key Laboratory of Safety Control of Bridge Engineering of Ministry of Education and Hunan Province, Changsha University of Science and Technology,Changsha 410114,China)
1674-2974(2017)09-0017-09
10.16339/j.cnki.hdxbzkb.2017.09.003
2016-09-05
国家重点基础研究发展计划(973计划)项目(2015CB057701,2015CB057702),National Program on Key Basic Research Project (973 Program) (2015CB057701,2015CB057702)
殷新锋(1980—),男,安徽岳西人,长沙理工大学副教授,博士
†通讯联系人,E-mail:yinxinfeng@163.com
TU311.3;TU352.1
A

