基于Teager能量算子和深度置信网络的滚动轴承故障诊断
陶洁,刘义伦,付卓,杨大炼,汤芳
基于Teager能量算子和深度置信网络的滚动轴承故障诊断
陶洁1, 2,刘义伦1, 3,付卓4,杨大炼1,汤芳1
(1. 中南大学机电工程学院,湖南长沙,410083;2. 湖南科技大学知识处理与网络化制造实验室,湖南湘潭,411201;3. 中南大学轻合金研究院,湖南长沙,410083;4. 长沙学院机电工程系,湖南长沙,410022)
针对传统的分类器对滚动轴承早期微弱故障进行诊断时泛化能力不强的问题,提出基于Teager能量算子(TEO)和深度置信网络(DBN)的滚动轴承故障诊断方法。先用TEO提取滚动轴承振动信号中的瞬时能量,构造相应的特征向量;采用层次优化算法调整DBN结构参数,生成合适的分类器。应用美国西储大学轴承实验振动信号,对不同类型、不同损伤程度的滚动轴承进行故障诊断,对比分析DBN、支持向量机(SVM)和邻近算法(KNN)的分类准确性。研究结果表明:DBN能更准确、稳定地识别滚动轴承各种故障,具有较强的泛化能力。
深度置信网络;Teager能量算子;滚动轴承;故障诊断
滚动轴承在机械设备中广泛应用,其使用过程通常经历了从正常到失效的演变。传统的故障诊断主要对滚动轴承的故障类型和部位进行研究,对早期微弱故障及其损伤情况研究较少[1]。事实上,许多设备出现早期轻微故障时并不需要停机或更换零部件,而及时准确地掌握滚动轴承的故障损伤情况,对保障机械设备安全运行、避免经济损失和灾难性事故具有重要的意义。Teager能量算子通过计算离散信号的机械能,对信号的瞬态变化具有较高的时间分辨率和较强的自适应能力[2],因此,可以利用TEO瞬时能量构造特征向量,以识别滚动轴承的各种故障。王天金等[3−6]利用Teager能量算子及其改进方法实现了滚动轴承的各种故障诊断,但这些研究中特征提取方法比较复杂,所采用的频谱分析法对轴承故障不同损伤程度的诊断结果不稳定。深度置信网络是一种新型的机器学习方法,其深层网络结构能从高维度大数据中逐层提取数据特征,实现数据的分类识别[7]。与传统的支持向量机(SVM)、最邻近距离(KNN)等浅层分类器相比,DBN避免了局部极值和数据维度灾难等问题,能更准确、高效地实现数据分类[8−9]。目前,DBN在语音、图像、手写体识别等领域[10−11]取得了良好效果,并在故障诊断领域得到初步应用。TRAN等[12]利用TEO提取压缩机的各种状态信号特征,用DBN对阀门故障进行模式识别;SUN等[13]应用DBN对电动机故障状态进行模式识别,取得较好的效果;TAMILSELVAN等[14]利用DBN对飞机发动机和变压器进行故障诊断;李艳峰等[15]采用DBN多分类器实现了滚动轴承的故障诊断,但要采集较长的振动信号进行奇异值分解。目前,对DBN结构设置大多仅凭经验得到合适的DBN分类器。为此,本文作者提出基于TEO和DBN的滚动轴承故障诊断方法,对不同类型不同损伤程度的轴承故障,通过层次优化算法生成DBN分类器,使模型具有较强的自适应性和泛化能力。
1 Teager能量算子解调法
KAISER[2]提出TEO信号分析法,用以跟踪非线性语音信号的瞬时能量。对于离散信号(),TEO定义为

(2)
()经TEO运算后得到

(3)

同理可得,()的瞬时频率和瞬时幅值为:
(5)

2 基于层次优化的DBN分类器
通常DBN的学习能力随隐层数和隐节点数的增加而提高,但当隐层数和隐节点数达到阈值后,盲目增加其数量可能导致DBN的识别能力下降[16]。在滚动轴承故障诊断中,DBN的模型结构需要与特征向量维度相适应,若DBN结构过于简单,则无法实现故障特征向量的分类识别;若DBN结构过于复杂,则不仅浪费训练时间,而且可能无法辨别故障信息。因此,本文提出层次优化算法,用TEO提取振动信号的瞬时能量,直接构造相应的特征向量;利用特征向量的维度设置隐层及隐节点临界值,根据训练样本集的分类错误率逐层优化调整DBN模型结构,得到合适的DBN分类器。图1所示为基于TEO和DBN的故障诊断基本过程。
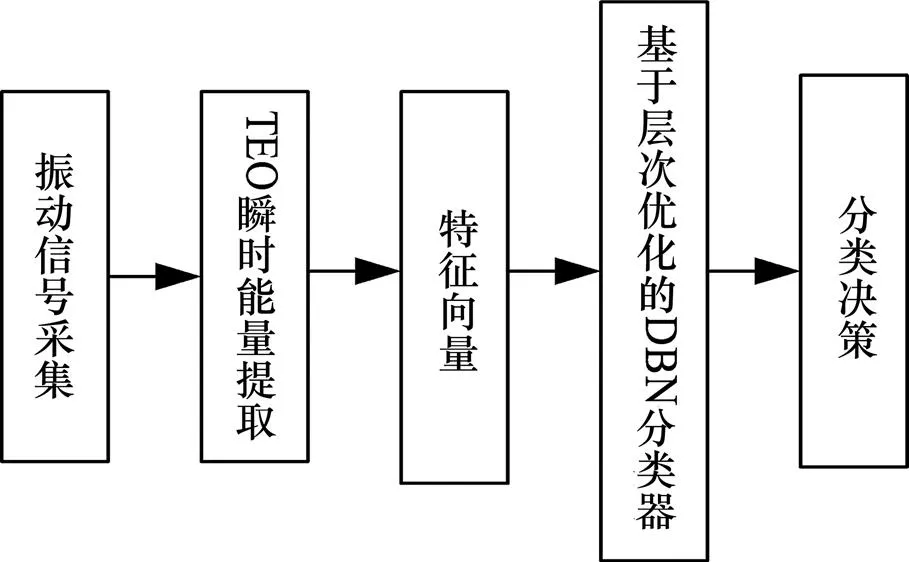
图1 基于TEO和DBN的故障诊断基本过程
2.1 DBN基本原理
DBN是一种基于能量的概率生成模型[9],由若干个受限玻尔兹曼机(restrict Boltzmann machine,RBM)和1个反向神经网络(BPNN)组成,其中一个RBM的隐层作为下一个RBM的显层,不断叠加构成DBN深层网络结构。图2所示为DBN的基本结构图,其中:v为显节点;h为隐节点;v和h有向全连接;为显节点偏置项;为隐节点偏置项;w为显节点到隐节点的连接权重;,和w构成模型的参数集;= 1, 2, 3;=1,2, 3。

图2 DBN基本结构图
给定显层向量,隐节点h的激活概率为

给定隐层向量,可视节点v的激活概率为
(8)

(10)
2.2 DBN层次优化算法
在DBN无监督训练过程中,通常采用批处理随机梯度下降法,来计算各节点的激活概率,调整节点的权值。因此,设置隐层及隐层结点数的临界值,并用训练集的分类准确率作为模型优化的阈值,逐层优化模型参数。若模型的分类准确率达到阈值,则生成DBN分类器,否则增加隐层数或隐节点数以得到合适的DBN分类器。图3所示为DBN层次优化算法流程图,步骤如下。
1) 初始化DBN结构参数:隐节点数,隐层数,学习率,隐节点临界值,隐层临界值,分类最小错误率,隐节点调整步长和学习率调整步长;构造参数集;=0,1,…,;=1,2,…,;=1,2,…,。
5) 若DBN的隐层数和隐节点数分别超出临界值和,则输出分类错误率最小的,得到DBN分类器。
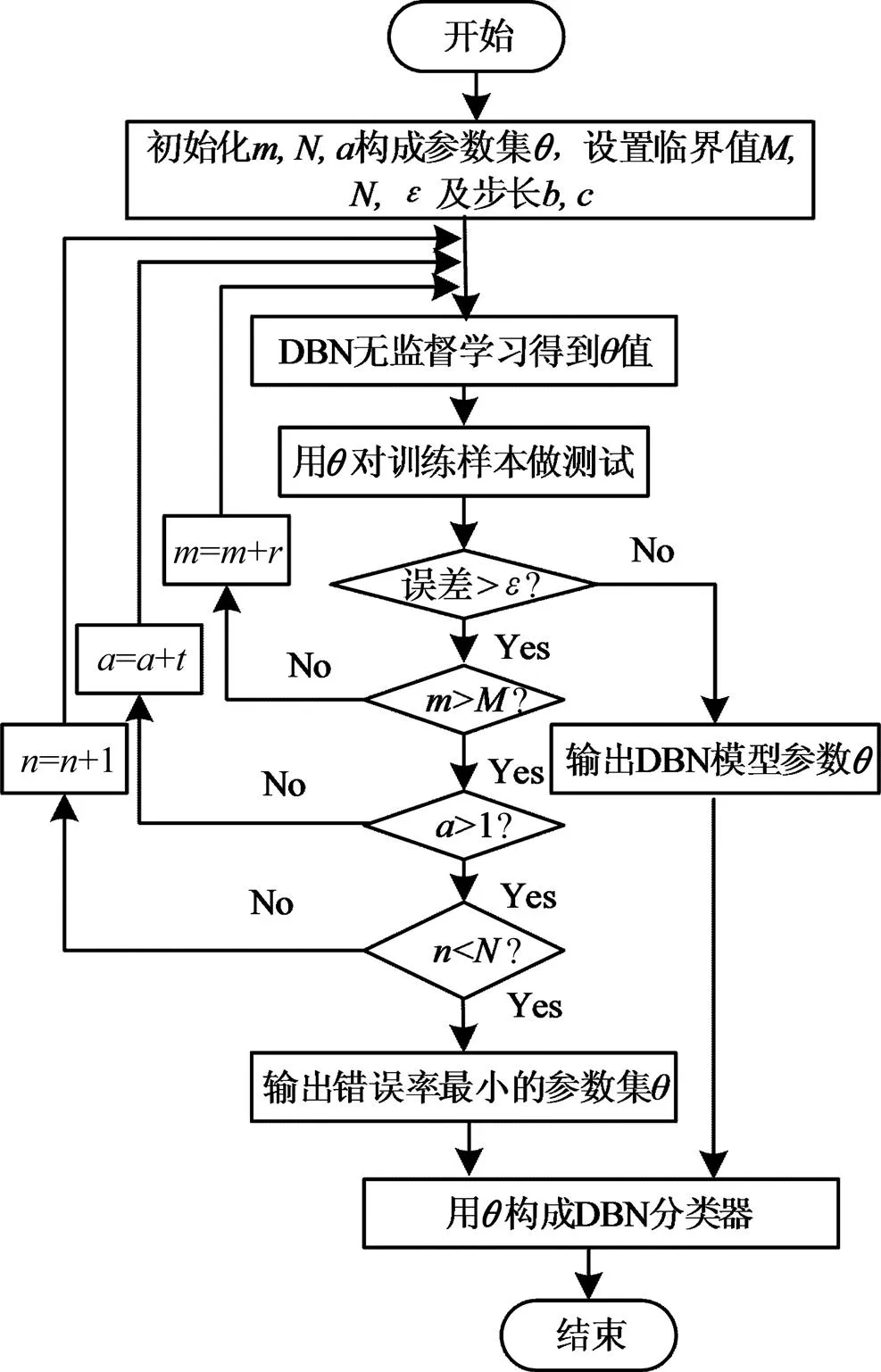
图3 DBN层次优化流程图
DBN无监督训练算法[8]步骤如下。
1) 显层初始化:0为输入样本向量,为参数集随机初始化,为迭代次数。
2) 利用式(7)和(8)计算特征向量0,1和1。
3) 利用式(9)得到RBM初始状态与更新状态下联合概率分布,代入式(10)修正参数集得到+1。
4) 取下一个训练样本,重复步骤2)和3)。
5) 重复步骤2)~4),迭代次。
6) 在模型顶端设置1个BPNN,用反向传播算法把误差传递回各层并对各层的参数进行微调,使整个模型的参数达到最优解。
3 应用实例分析
3.1 数据来源
为验证所提方法的可行性和有效性,采用美国西储大学电气工程实验室轴承实验振动信号数据[17],分别对滚动轴承内圈、外圈、滚动体的故障信号进行模式识别。
实验台主要由1.47 kW电动机、扭矩传感器、译码器、电器控制、测力器等装置组成,实验轴承为SKF公司生产的6205-2RS深沟球轴承。实验中,故障轴承安装在电机的驱动端,采样频率为12 kHz,转速为1 797 r/min,不同损伤程度的故障点蚀直径分别为0.18,0.36和0.53 mm,点蚀深度均为0.28 mm。
图4所示为各种状态下滚动轴承的振动信号时域波形图。从图4可以看到各种振动信号的波形比较相似,难以区分故障的类型及损伤程度。

(a) 正常轴承;(b) 内圈点蚀直径0.18 mm;(c) 内圈点蚀直径0.36 mm;(d) 内圈点蚀直径0.53 mm;(e) 外圈点蚀直径0.18 mm;(f) 外圈点蚀直径0.36 mm;(g) 外圈点蚀直径0.53 mm;(h) 滚动体点蚀直径0.18 mm;(i) 滚动体点蚀直径0.36 mm;(j) 滚动体点蚀直径0.53 mm
3.2 TEO瞬时能量特征提取
当滚动轴承有局部损伤时,其损伤点通过其他元件时会出现振动能量突变,而不同类型的故障引起能量突变的程度和时间不同[3]。基于TEO特征提取的步骤如下。
1) 采集轴承旋转1周的信号采样点构成1个数据样本=[1,2,…,x];个数据样本构成振动信号样本集={1,2,…,}。
2) 利用式(6)计算的瞬时幅值得到A=[1,2,…,a],由振动信号样本集={1,2,…,}得到瞬时振幅样本集={1,2,…,}。
3) 对瞬时振幅进行归一化处理,得到TEO瞬时特征向量=[1,2,…,e]。其中,。由瞬时振幅样本集={1,2,…,}构成TEO特征向量集={1,2,…,}。
根据上述步骤,每段截取400个信号采样点构成1个数据样本(即试件旋转1周的振动信号作为1个数据样本)。在每种状态下,连续采集40 000个振动信号,构成100个数据样本,数据集如表1所示。其中:A,B和C为不同故障类型的滚动轴承振动信号数据;D,E和F为不同损伤程度的振动信号数据。在每种状态下选取100个数据样本构成训练集,另外随机选取100个数据样本构成测试集。对表1中振动信号提取TEO瞬时能量,各种信号样本提取的TEO瞬时能量特征波形如图5所示。
由图5可知:整个TEO特征向量不仅保留了故障信号能量冲击、周期、幅值等方面的特性,而且记录了能量变化的时间点。因此,可以通过TEO瞬时能量序列来描述故障类型及其损伤情况。
3.3 诊断结果与分析
实验中,初始化DBN模型参数,隐节点数=50,隐层数=1,学习率=0.1,隐节点阈值400,隐层数阈值=4,分类准确率阈值0.03,隐节点数增加步长10,学习率增加步长=0.1,用训练集对模型进行无监督训练。若训练集的分类错误率小于或等于0.03,则用构成DBN分类器;若训练集错误率大于0.03,则增加DBN隐层数或隐层节点数,提高DBN模式识别的准确率;若隐层数和隐层节点数超出阈值,则输出训练集错误率最小的参数集构成DBN分类器。6组实验的DBN模型结构参数如表2所示。
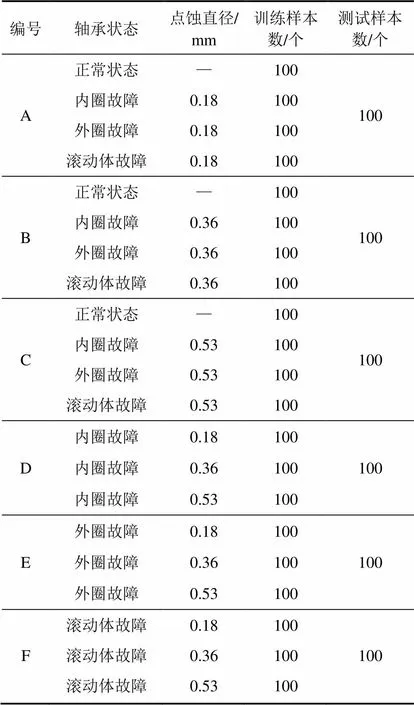
表1 轴承故障样本参数
由表2可知:6组实验中故障类型(A,B和C)分类器的隐层数和隐层节点数比故障程度(D,E和F)分类器要少;滚动体(F)损伤程度诊断的隐层数比内圈(D)和外圈(E)的隐层数要多。
DBN分类器的学习能力主要由隐层数和隐节点数决定。层次优化算法得到结构相对简单的DBN即可完成故障类型的诊断,说明滚动轴承故障类型的诊断相对损伤程度诊断要容易[1]。在损伤程度故障诊断中,由于滚动体表面出现局部损伤时不仅有滚动现象,而且有滑动现象,而滚动体的损伤点不能与内圈或外圈保持周期性接触,从而导致滚动体故障的振动信号出现随机性,使滚动体的故障诊断相对内、外圈的故障诊断困难。实验中,内圈(D)和外圈(E)的损伤程度诊断采用2层DBN模型结构即可完成分类识别任务,对于特征复杂的滚动体(F)损伤程度诊断,则需要增加隐层数及隐层节点数才能使DBN拥有更强的学习能力,完成滚动体故障程度的分类识别。

(a) 正常轴承;(b) 内圈点蚀直径0.18 mm;(c) 内圈点蚀直径0.36 mm;(d) 内圈点蚀直径0.53 mm;(e) 外圈点蚀直径0.18 mm;(f) 外圈点蚀直径0.36 mm;(g) 外圈点蚀直径0.53 mm;(h) 滚动体点蚀直径0.18 mm;(i) 滚动体点蚀直径0.36 mm;(j) 滚动体点蚀直径0.53 mm

表2 不同实验中DBN模型结构参数
为验证DBN模式识别的性能,选择最邻近距离分类器(KNN)和支持向量机(SVM)进行对比实验。其中SVM采用径向基函数惩罚因子为0.993 2,核参数为1.082 3,KNN采用欧式距离作为判别标准。3个分类器对训练集和测试集的故障诊断结果分别如表3和表4所示。

表3 训练集分类准确率
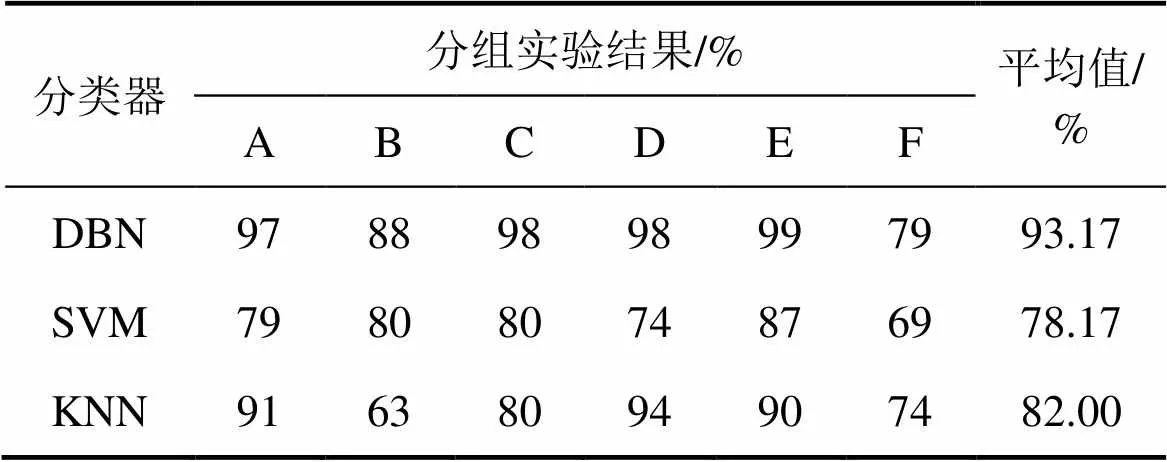
表4 测试集分类准确率
从表3和表4可见:DBN对训练集的平均分类准确率为94.67%,对测试集的平均分类准确率为93.17%;SVM对训练集的平均分类准确率98.83%,对测试集的平均分类准确率为78.17%;KNN对训练集平均分类准确率为90.50%,对测试集平均分类准确率为82.00%。
DBN,SVM和KNN都是对训练集进行学习后对测试数据进行分类,但分类的稳定性和泛化能力不同。如图6所示,试验中DBN对训练集和测试集的分类准确率基本吻合,表现出较强的泛化能力。在D组实验中,受层次优化阈值的约束,DBN训练集的准确率为97.00%,对测试集的准确率为98.00%。SVM对训练集的分类效果很好,对测试集的分类准确率却明显下降。KNN对训练集分类准确率随训练准确率变化而变化,但都下降了5%~10%。

(a) DBN诊断结果;(b) SVM诊断结果;(c) KNN诊断结果
实验中,训练集从各种故障状态下顺序选取数据样本,并有序地构成训练样本集;而测试集中是从各种状态下随机选取样本构成测试集,无论是样本所属类别和样本排列顺序都是随机的。SVM对数据进行分类识别时,主要依靠样本集对基函数进行训练,而基函数的训练对样本质量及样本分布依赖性较大[8]。KNN对数据进行分类识别时,主要由距离函数决定分类器的效果,而距离函数一旦选定就不能变换,因此,SVM和KNN对训练集的准确率较高,对测试集的准确率明显下降。DBN作为一种基于概率的学习模型,对数据样本具有较强的无监督学习能力,对训练集和测试集的分类准确性比较稳定,表现出较强的泛化能力。
4 结论
1) 基于TEO和DBN的故障诊断方法,直接采用滚动轴承旋转1周的瞬时能量作为特征向量,避免了冗长的信号采集和复杂的特征提取。
2) 与传统的分类器相比,DBN对高维度数据无监督学习能力,使分类准确率更加稳定。
3) 在不同类型、不同损伤程度的滚动轴承故障诊断中,通过层次优化算法调整DBN结构参数,使分类器具有较强的自适应能力。
[1] 王国彪, 何正嘉, 陈雪峰, 等. 机械故障诊断基础研究“何去何从”[J]. 机械工程学报, 2013, 49(1): 63−72.WABG Guobiao, HE Zhengjia, CHEN Xuefeng, et al. Basic research on machinery fault diagnosis:what is the prescription[J]. Journal of Mechanical Engineering, 2013, 49(1): 63−72.
[2] KAISER J F. On a simple algorithm to calculate the ‘energy’ of a signal[C]// Proceedings of IEEE International Conference on Axoustics, Speech, and Signal Processing. Piscataway, NJ, 1990: 381−384.
[3] 王天金, 冯志鹏, 郝如江, 等. 基于Teager能量算子的滚动轴承故障诊断研究[J]. 振动与冲击, 2012, 31(2): 1−5. WANG Tianjin, FENG Zhipeng, HAO Rujiang, et al. Fault diagnosis of rolling element bearing based on Teager energy operator[J]. Journal of Vibration and Shock,2012, 31(2): 1−5.
[4] 胥永刚, 崔涛, 马朝永, 等. 基于LCD和Teager能量算子的滚动轴承故障诊断[J]. 北京工业大学学报, 2015, 41(3): 340−346. XU Yonggang, CUI Tao, MA Chaoyong, et al. Fault diagnosis of bearing based on LCD and Teager energy operator[J]. Journal of Beijing University of Technology, 2015, 41(3): 340−346.
[5] 杨青乐, 梅检民, 肖静, 等. Teager能量算子增强倒阶次谱提取轴承微弱故障特征[J]. 振动与冲击, 2015, 34(6): 1−5.YANG Qingle, MEI Jianmin, XIAO Jing, et al. Weak fault feature extraction for bearing based on order cepstrum enhanced by Teager energy operator[J]. Journal of Vibration and Shock, 2015, 34(6): 1−5.
[6] 梅检民, 赵慧敏, 陈祥龙, 等. Teager算子和极坐标级联增强时频特征算法及轴承微弱故障特征提取[J]. 振动工程学报, 2014, 17(1): 152−158. MEI Jianmin, ZHAO Huimin, CHEN Xianglong, et al. Cascading enhancement of time-frequency feature based on Teager energy operator and polar diagram and its application of extracting bearing’s weak fault[J]. Journal of Vibration Engineering, 2014, 17(1): 152−158.
[7] HINTON G E, OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527−1554.
[8] 袁胜发, 褚福磊. 支持向量机及其在机械故障诊断中的应用[J]. 振动与冲击, 2007, 26(11): 29−35. YUAN Shengfa, CHU Fulei. Support vector mechines and its Applications in machine fault diagnosis[J]. Journal of Vibration and Shock, 2007, 26(11): 29−35.
[9] HINTON G E, SALAKHUTDINOV R. Reducion the dimensionality of data with neural networks[J]. Science, 2006, 313: 504−507.
[10] 陈宇, 郑德权, 赵铁军. 基于Deep Belief Nets的中文名实体关系抽取[J]. 软件学报, 2012, 23(10): 2572−2585. CHEN Yu, ZHENG Dequan, ZHAO Tiejun. Chinese relation extraction based on deep belief nets[J]. Journal of Software, 2012, 23(10): 2572−2585.
[11] SCHMIDHUBER J. Deep learning in neural networks: an overview[J]. Neural Networks, 2015, 61(9): 85−117.
[12] TRAN V T, ALTHOBIANI F, BALL A. An approach to fault diagnosis of reciprocating compressor valves using Teager-Kaeser energy operator and deep belief networks[J]. Expert Systems with Application, 2014, 41(9): 4113−4122.
[13] SUN J, WYSS R, STEINECKER A, et al. Automated fault detection using deep belief networks for the quality inspection of electromotors[J]. tm-Technisches Messen, 2014, 81(5): 255−263.
[14] TAMILSELVAN P, WANG Yibin, WANG Pingfeng. Deep belief network based state classification for structural health diagnosis[J]. Reliability Engineering and System Safety, 2013, 115(3): 124−135.
[15] 李艳峰, 王新晴, 张梅军, 等. 基于奇异分解和深度置信网络多分类器的滚动轴承故障诊断方法[J]. 上海交通大学学报, 2015, 49(5): 681−686. LI Yanfeng, WANG Xinqing, ZHANG Meijun, et al. An approach to fault diagnosis of rolling bearing using SVD and multiple DBN classifiers[J]. Journal of Shanghai Jiaotong University, 2015, 49(5): 681−686.
[16] 刘建伟, 刘媛, 罗雄麟. 深度学习研究进展[J]. 计算机应用研究, 2014, 31(7): 1921−1930. LIU Jianwei, LIU Yuan, LUO Xionglin. Research and development on deep learning[J]. Application Research of Computers, 2014, 31(7): 1921−1930.
[17] LOPAROK A. Bearings vibration dataset, case western reserve university[EB/OL]. [2015−06−18]. http://www.eees.ewru.edu/ laboratory/bearing/download.htm.
(编辑 陈灿华)
Fault damage degrees diagnosis for rolling bearing based on Teager energy operator and deep belief network
TAO Jie1, 2, LIU Yilun1, 3, FU Zhuo4, YANG Dalian1, TANG Fang1
(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;2. Key Laboratory of Knowledge Processing and Networked Manufacturing, Hunan University of Science and Technology, Xiangtan 411201, China;3. Light Alloy Research Institute, Central South University, Changsha 410083, China;4. Department of Mechanical and Electrical Engineering, Changsha University, Changsha 410022, China)
Considering that the traditional classifiers’ generalization ability is not strong in the early fault diagnosis of rolling bearings, the fault diagnosis method based on Teager energy operator (TEO) and deep belief network (DBN) were put forward. Firstly, the instantaneous amplitudes of the vibration signal were calculated by TEO, and the instantaneous energies of the signal were extracted. Then the characteristic vectors were constituted with the instantaneous energies. DBN classifiers were used to identify the faults of rolling bearing. For different types of fault diagnosis, DBN structure parameters were adjusted according to the classification error rate of training sets. Using the bearing fault experiments’ data of American West Storage University, the classification accuracy of SVM and KNN was compared. The results show that the suggested methods are more effective and stable for the identification of rolling bearing fault diagnosis in various situations.
deep belief network; Teager energy operator; rolling bearings; fault diagnosis
10.11817/j.issn.1672-7207.2017.01.009
TAH133.33
A
1672−7207(2017)01−0061−08
2016−01−02;
2016−03−22
国家自然科学基金资助项目(51375500);国家重点基础研究发展计划(973计划)项目(2014CB046300);湖南省科技计划项目(2016GK2005) (Project(51375500) supported by the National Natural Science Foundation of China; Project(2014CB046300) supported by the National Basic Research Development Program (973 Program) of China; Project(2016GK2005) supported by Key Research and Development Projects of Hunan Province)
刘义伦,博士,教授,从事信号处理与机械故障诊断研究;E-mail: ylliu@csu.edu.cn

