航天器蓄电池放电发热量测试方法系统误差分析

王亚龙，孙腾飞，王帅，杨居翰，朱其荫



航天器蓄电池放电发热量测试方法系统误差分析

王亚龙，孙腾飞，王帅，杨居翰，朱其荫

（北京空间飞行器总体设计部空间热控技术北京市重点实验室，北京100094）

蓄电池发热量是航天器蓄电池热控设计的重要参数，其测试准确度直接影响热控设计状态和在轨工作温度。文章采用真空绝热量热法对蓄电池发热量测试系统进行了漏热分析，并给出了修正方法；以模拟蓄电池为研究对象，分析了蓄电池发热量测试误差，并提出了改善系统测量准确度的解决方案。结果表明，当放电时间大于1h，航天器蓄电池发热功率在2～25W范围内时，测试误差不超过6%，且发热功率越大误差越小；当发热功率大于10W时，测试误差不超过3%，可以满足工程要求；对于发热功率较小（绝对值小于0.5W）的小电流放电或充电，测试误差较大，但绝对值仍然较小，对实际工程影响不大。

航天器蓄电池；真空绝热量热法；发热量；系统误差

0 引言

在地影期、发射主动段、太阳电池板展开之前，航天器上仪器设备均由蓄电池组供电[1]。蓄电池组放电时会因自身发热引起温度显著变化，而其对工作温度范围与单体间温差有严格要求[2-4]，若不能对蓄电池进行有效的热控制，则蓄电池不但不能在最佳状态下工作，而且使用寿命会极大地缩短，进而直接影响到航天器的寿命。因此，对蓄电池正常充放电条件下的比热容、发热量等热特性进行研究，对于蓄电池组热控设计具有非常重要的意义[5-7]。

为了研究蓄电池充放电热特性，国内外众多研究者针对不同蓄电池类型建立了相应的热学模型[8-10]，目前的蓄电池热学模型理论描述相差不大，并且均需要通过试验方法获得。绝热量热法是使用最为广泛的一种热特性测量手段[11-12]，目前我国的绝大多数航天器单体蓄电池发热量均通过这种方法获得[13-14]。但由于试验中无法保证蓄电池处于理想绝热状态，蓄电池与环境之间存在漏热，从而影响该测试方法的准确性；由于测试系统比较复杂并且测试精度要求高，导致系统误差难以量化，特别是在蓄电池发热功率较小时难度更大；由于蓄电池表面温度不均匀[5]，所以必须合理设计试验系统，并仔细观察试验过程，及时进行必要的近似处理。

本文建立了绝热量热法测试试验平台，进行了蓄电池发热量测量过程漏热分析，并给出了测量结果修正方法；以模拟蓄电池为研究对象，试验研究了蓄电池在不同发热功率下的测试误差，结果可用于指导后续试验误差评估。

1 试验原理

理想热学试验应遵循2条基本原则：其一是保持系统为孤立系统；其二是测量一个系统的状态参量时，保持系统处于稳态[15]。对于一个孤立系统，系统内部所产生的热量全部被系统自身所吸收，即在绝热的情况下，物体所产生的热量全部用于系统自身的温度变化。

在绝热条件下，蓄电池的产热速率是蓄电池内部产热以及蓄电池各组分的比热容的函数。在真空绝热环境下，试件吸收或放出的热量用于自身温度的上升。可以根据试件的温升、比热容和质量来计算其发热量。对于实际试验系统，考虑系统向外散热损失，由热平衡方程可得

=(Δ放电–Δ系漏Δ放电)， (1)

式中：为试件发出或吸收的热量，J；为试件的比热容，J/(kgK)；为试件的质量，kg；Δ放电为试件的温升，K；Δ系漏为系统漏热率，K/s；Δ放电为放电时间，s。

当试件自身不发出或吸收热量，即=0时，即可得到系统漏热率

Δ系漏=(末–始)/(末–始)， (2)

式中：末和始分别为试件的终止和初始温度；末和始分别为试验终止和初始时间。

实际试验中，加在试件上的热功率绝大多数用于试件自身温度的上升，试件比热容可根据电加热器阻值、加热电流以及被试件温升计算得到，即：当试件通过电加热器输入恒定功率时，其比热容为

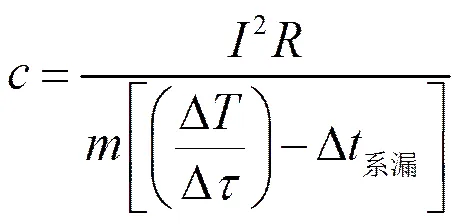
式中：为电加热器加热电流，A；为加热器电阻，Ω。

将式(2)、(3)代入式(1)，即可得到蓄电池放电时的发热量。

2 试验装置

试验装置主要由真空容器、防护筒、模拟蓄电池、温度传感器和温差热电偶等组成，如图1所示。模拟蓄电池用低导热率的尼龙绳悬挂在防护筒内，以减小蓄电池的传热损失；蓄电池外表面与防护筒内表面之间用低发射率隔热膜来减少辐射散热。试验时容器内抽高真空，利用温差热电偶进行跟踪控温，保证防护筒与蓄电池的温度一致，以尽量减少蓄电池向外界漏热。

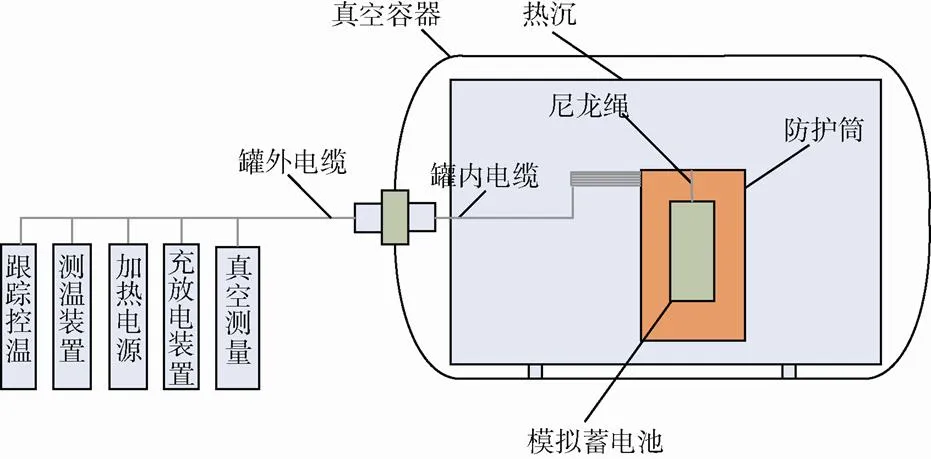
图1 试验系统示意图

目前航天器常用的蓄电池有镉镍蓄电池、氢镍蓄电池、锂离子蓄电池等，各类蓄电池的比热容一般在800～1100J/(kgK)之间。为了更准确测定蓄电池发热量误差范围，模拟蓄电池为与常用单体蓄电池的比热容和外形尺寸等均较为接近的空心圆柱体（材质为硬铝2A12，尺寸为100mm×160mm，质量为2.096kg）。防护筒为由2mm厚的紫铜板制成的圆柱筒（尺寸为220mm×360mm），带有上、下平盖，安装方式如图2所示。

图2 蓄电池单体发热量测试安装示意图

试验中的主要设备包括KM1真空容器、电子天平、Agilent 34980A万用表、Euro3504温控仪、Agilent 6655A电源，试件在KM1内的安装状态见图3。

图3 试件安装状态

3 系统漏热分析与修正

3.1 系统漏热分析

对于蓄电池发热量测试，理想状态是在绝热环境下测量蓄电池的自身温度变化。但实际试验中无法模拟理想绝热状态，蓄电池辐射漏热、导热漏热、加热器及传感器自身热容对测量结果均有影响。绝热量热法测试为稳定测试方法，故本文按稳态状态建立数学模型，对漏热进行分析。

系统漏热主要由3部分组成，即

系漏=1+2+3， (4)

其中：1为辐射漏热；2为导热漏热；3为加热器及传感器的自热。

3.1.1 辐射漏热分析

防护筒表面的加热回路与蓄电池单体和防护筒上的控温热电偶对组成跟踪控温加热器，保证二者温度一致，从而为蓄电池单体提供一个绝热的环境。试件与防护筒之间的辐射换热可以通过两者所处的温度和蓄电池的几何尺寸、表面发射率确定，即

1=电池()， (5)

其中：为等效发射率；为斯忒藩–玻耳兹曼常量；电池为蓄电池表面积；电池和防护筒分别为蓄电池和防护筒的平均温度。

图4为蓄电池温度为20℃时，不同发射率及温差对辐射漏热功率的影响。可以看出，跟踪控温温差在1℃以内时，减小发射率可以大幅减小辐射漏热损失。在蓄电池外表面与防护筒内表面加双面镀铝薄隔热膜，其等效发热率将小于0.05，此时蓄电池与防护筒的辐射换热功率将减小到0.02W以内，蓄电池的辐射漏热可以忽略不计。

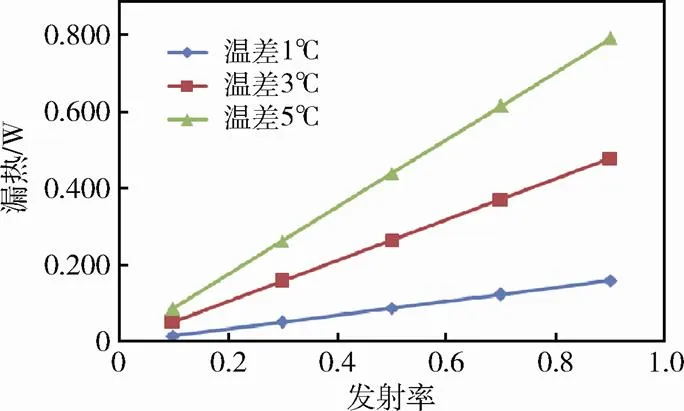
图4 不同发射率及温差对辐射漏热功率的影响

3.1.2 导热漏热分析

蓄电池单体通过尼龙绳吊挂在防护筒内，充放电引线、加热器引线和测控传感器引线均连接到罐外测试设备，即蓄电池与外界存在导热漏热。防护筒与蓄电池温度基本一致，且尼龙绳导热率较低，因此通过吊挂尼龙绳的漏热可以忽略不计。防护筒内外环境温度差异很大，蓄电池与外部之间存在较大的导热漏热，这一部分热量通过导热与辐射传递走。按照傅里叶定律，有

2=-电缆(d/d)， (6)

该试验系统的罐内充放电及电加热电缆共64根镀银铜导线，导线的规格为AF200 19×0.16，单根导线面积约0.382mm2。根据以往试验经验，取电缆集束100mm长度的温度变化量为20℃。铜的导热系数为386W/(mK)，通过充放电电缆的导热漏热量为。

试验中热电偶共16对，热电偶丝的直径约为0.2mm，单根导线面积约0.0314mm2。同样，取电缆束100mm长度的温度变化量为20℃。康铜的导热系数为20.2W/(mK)，通过热电偶测试电缆的导热漏热为。

因此，总的导热漏热量为1.92W。其中充放电及加热电缆的导热漏热对测试结果影响较大，测温传感器引线的导热漏热可以忽略不计。电缆皮的导热系数远远小于铜的导热系数，故尽管其截面积较大，但是通过电缆皮的导热漏热仍远小于通过导线的导热漏热，可以忽略不计。

3.1.3 加热器及传感器自热分析

电加热器加热功率一部分用于蓄电池温升，另一部分用于电加热片及传感器自身温升。1m长热电偶的质量约为1g左右；电加热片由聚酰亚胺膜、康铜丝组成，质量约为4～6g，远小于蓄电池的质量，因此在同样温升情况下，电加热片及传感器自身带走的热量可忽略不计。

3.2 系统漏热修正

由以上分析可知系统漏热主要为电缆导热漏热。为了减小电缆导热漏热，需对蓄电池单体充放电电缆进行漏热补偿跟踪控温，并且对测、控温热电偶引线从蓄电池单体表面开始直至过渡插座处均包覆双面镀铝聚酯膜，如图5所示。采取漏热控制措施后，漏热可以减小到0.1W以内。

图5 蓄电池单体电缆漏热补偿跟踪控温示意图

漏热修正值仅为温度的函数。为确定系统漏热损失大小，利用KM1试验测试系统，选择一般蓄电池正常工作温度范围（-10～40℃），对不同温度点下的系统漏热率进行了测试，结果见表1。

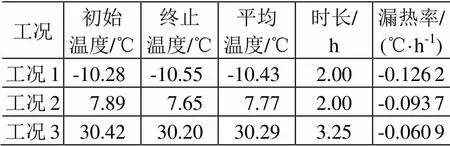
表1 系统漏热率测试结果

通过对漏热率与模拟蓄电池平均温度进行拟合，可得到不同温度下的系统漏热率为

Δ系漏=0.001平均–0.108， (7)

在计算蓄电池发热量时，通过式(2)和式(7)计算得到该过程中的系统漏热率修正值，再通过式(1)即可得到修正后蓄电池的发热量。

4 试验工况及结果分析

根据试验要求及测试原理，在真空室内进行比热容及发热量测试。真空室热沉采用液氮制冷，压力小于1.3×10-3Pa。由3.1.1节辐射漏热分析可知，当模拟蓄电池温度均匀，防护筒与模拟蓄电池间温差小于1℃时，即可认为蓄电池处于绝热状态。

测量误差主要是仪表基本误差，其次是附加误差，在正常使用条件下附加误差可以忽略，仪表测量误差见表2。

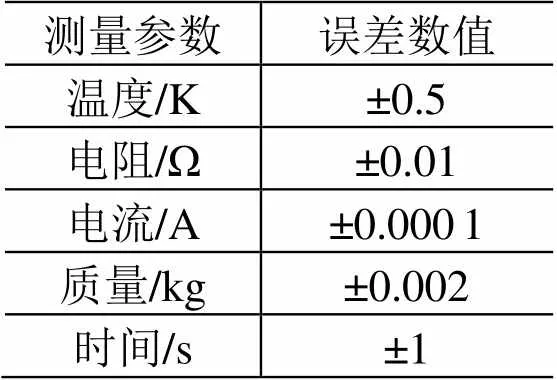
表2 仪表测量误差

根据发热量计算公式，得到发热量的误差传递函数为

其中根据公式(3)测得模拟蓄电池的比热容= 900.48J/(kgK)。

通过式(8)可以得到各参数测试误差变量对发热功率误差的影响因子。假设模拟蓄电池加热时长均为1h，系统误差与测温精度的关系如图6所示。可以看出，系统误差随着仪表测温精度的提高而减小，在发热功率较小的情况下尤为明显。当测温精度由0.5K提高到0.1K时，发热功率为2W时的系统误差可由13.5%减小到3.0%，发热功率为25W时的系统误差可由1.5%减小到0.7%。由此可以看出，当加热时长一定时，在不同加热功率下，仪表测温精度显著影响测试结果。提高测量仪器精度，特别是提高测温精度可以进一步减小系统误差。

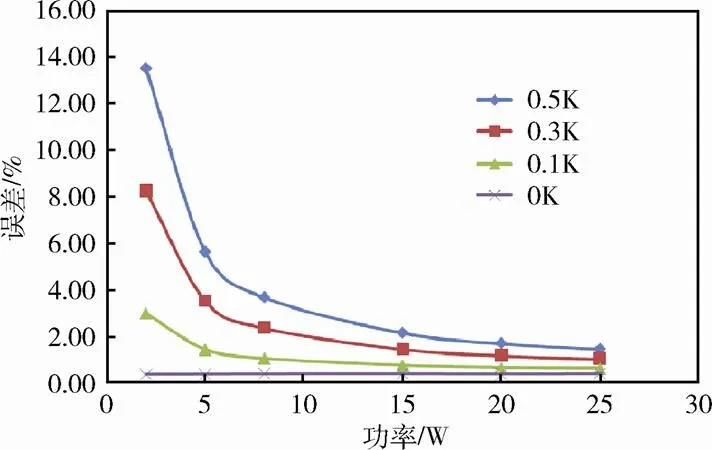
图6 不同测温精度时系统误差变化曲线

同样根据公式(8)，假设测温系统精度为0.5K，系统误差与加热时长的关系如图7所示。可以看出，加热功率为2W时，当加热时长由0.5h增加到2.5h时，系统理论误差可由16.7%减小到5.7%。系统误差随着加热时间的增加而减小，当加热时间小于1h时，系统误差快速增加，时长将显著影响系统误差。因此在实际试验中，特别当蓄电池放电功率较小时，延长测试时间可大大减小系统误差。

图7 不同放电时长下系统误差变化曲线

单体蓄电池充放电发热功率一般在0～25W范围内，在此功率区间内分6个工况进行了测试，加热时长均为1h，结果见表3。表中的温度为蓄电池外表面平面温度。

【中医解读】亢龙有悔、飞龙在天等招式，让不少武侠迷心存向往。从某种意义上来说，动物的确是人类的养生导师。通过模仿动物来强身健体，是我国传统的保健方式。

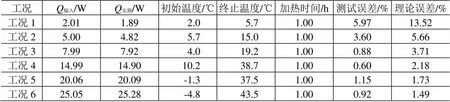
表3 不同发热功率下系统误差结果

图8为不同功率下系统理论误差与实测误差比较。可以看出，系统理论误差与实测误差变化趋势基本一致，实测误差小于理论误差，其主要原因是测量仪器真实误差小于其最大基本误差。当加热时长超过1h，蓄电池发热功率在2～25W时，测试误差小于6%，测试误差随着发热功率的增大而减小。当蓄电池发热功率小于10W时，随着发热功率的增大，测试误差呈线性快速减小，其原因是发热功率较小时，蓄电池温度变化速率较小，温度变化量较小，测温精度对测试结果产生显著的影响，与图6的分析结果一致。当蓄电池发热功率大于10W时，测试误差随着蓄电池发热功率增大趋于稳定，发热功率测试误差可以控制在3%以内。单体蓄电池在小电流放电或充电时，发热功率通常小于0.5W，此时，其发热量测试误差将会放大很多，但其绝对值仍然较小，对实际工程影响不大。

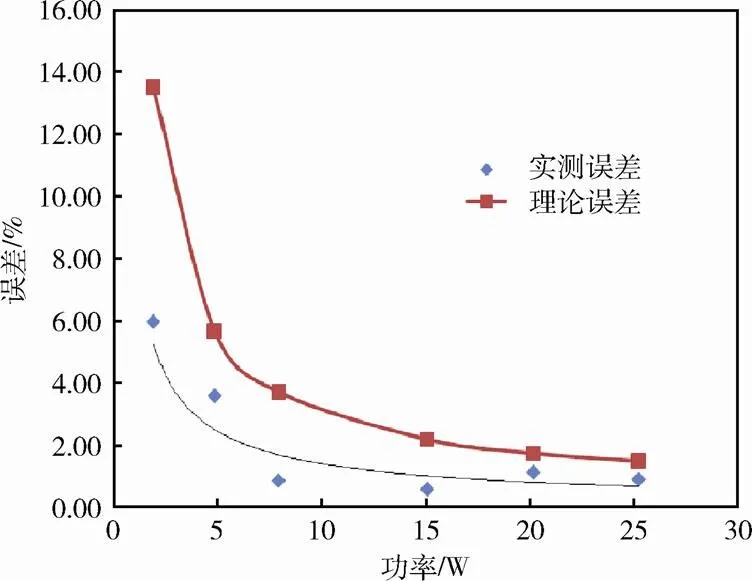
图8 不同功率下系统理论误差与实测误差比较

5 某型号锂离子蓄电池放电发热量测试

采用上述方法，对某型号50AhNCA锂离子蓄电池进行了比热容和放电发热量测试，测试所用设备与前述相同。该锂离子蓄电池的尺寸为55mm×240mm，质量为1.074kg。试验前首先对系统漏热进行了测试，通过漏热测试数据得到

Δ系漏=0.014平均–0.892。 (9)

表4为50AhNCA锂离子蓄电池在不同放电温度下发热量测试结果，放电始初状态蓄电池均充满电。试验中测得其比热容为1150.7J/(kgK)。

表4 50Ah锂离子蓄电池系统误差结果

注：其中20%DOD表示放电深度为20%。

试验过程中，蓄电池温度随放电时间的变化如图9所示：在放电初始阶段，蓄电池温度没有明显变化；当放电时间超过10min后，蓄电池处于稳态，蓄电池温度呈线性增长。表4中的发热功率实测为蓄电池在稳态下测得的结果。由表4可以看出，当放电电流为25.0～30.0A，放电时间由72min缩短到30min时，系统理论误差由7.4%增加到29.05%，与上一节分析结果一致。当蓄电池放电电流为34.5A，放电时间为72min时，随着放电初始温度的升高，蓄电池发热功率由6.58W减小到4.60W，减小30.1%，主要原因为低温时电化学体系极化高，反应活性降低，锂离子迁移速率变慢，电池内阻比高温时大，产热速率快。

图9 蓄电池温度随放电时间的变化

6 结束语

本文采用真空绝热量热法，对蓄电池发热量测试过程的漏热进行了分析，并给出了修正方法，探讨了测试系统误差及改善系统测量准确度的解决方案。结果表明提高测控温精度、延长放电测试时间可以进一步减小系统误差，特别在蓄电池发热功率较小时对系统误差有显著影响。

以模拟蓄电池为研究对象，通过试验研究了单体蓄电池在不同发热功率下的误差范围，试验测试误差与理论误差基本一致。需要说明的是，每类电池组分不一样，实际的蓄电池单体表面温度是不均匀的，各部位温度变化幅度略有差异，需仔细观察试验过程中各区域温度的变化。

（References）

[1] 马卉, 赵海峰. 航天器用蓄电池充电控制技术的研究与探索[J]. 电源技术, 2009, 33(6): 519-522

MA H, ZHAO H F. Research and exploration of battery charging control technology for aerocraft[J]. Chinese Journal of Power Sources, 2009, 33(6): 519-522

[2] 乔明, 陈琦, 曾毅, 等. 航天器用氢镍蓄电池钝化技术研究[J]. 航天器环境工程, 2012, 29(1): 83-87

QIAO M, CHEN Q, ZENG Y, et al. Passivation of hydrogen-nickel batteries for spacecraft[J]. Spacecraft Environment Engineering, 2012, 29(1): 83-87

[3] 刘百麟, 周佐新. 热控涂层红外发射率对GEO卫星蓄电池温度波动的影响[J]. 航天器环境工程, 2012, 21(6): 54-59

LIU B L, ZHOU Z X. Effect of thermal control battery temperature coatings infrared emittance on variation in GEO satellite[J]. Spacecraft Environment Engineering, 2012, 21(6): 54-59

[4] JOSSEN A, SPATH V, DORING H, et al. Battery management systems (BMS) for increasing battery life time[C]//The 21stInternational Telecommunication Energy Conference. Copenhagen, 1999. Doi: 10.1109/INTLEC.1999.794018

[5] 刘恒伟, 李建军, 谢潇怡, 等. 加速量热仪在锂离子电池热测试中的应用[J]. 集成技术, 2015(1): 51-59

LIU H W, LI J J, XIE X Y, et al. Application of accelerating rate calorimeter in the lithium-ion battery thermal test[J]. Journal of Integration Technology, 2015(1): 51-59

[6] CHACKO S, CHUNG Y M. Thermal modeling of Li-ionpolymer battery for electric vehicle drive cycles[J]. Journal of Power Sources, 2012, 213: 296-303

[7] EDDAHECH A, BRIAT O, VINASSA J M. Thermal characterization of a high-power lithium-ion battery: potentiometric and calorimetric measurement of entropy changes[J]. Energy, 2013, 61: 432-439

[8] 何常明, 许思传, 陈磊涛, 等. 车载镍氢电池热学模型的建立与试验[J]. 同济大学学报（自然科学版）, 2012, 40(10): 1548-1553

HE C M, XU S C, CHEN L T, et al. Thermal model and experimental investigation of vehicle-mounted Ni-MH power battery[J]. Journal of Tongji University (Natural Science), 2012, 40(10): 1548-1553

[9] NELSON P, DEES D, AMINE K, et al. Modeling thermal management of lithium-ion PNGV batteries[J]. Journal of Power Sources, 2002(110): 349

[10] SHI J Z, WU F. Thermal analysis of rapid charging nickel/metal hydride batteries[J]. Journal of Power Sources, 2006(157): 592

[11] 胡巩, 陈则韶. 量热技术和热物性测定[M]. 合肥: 中国科学技术大学出版社, 2009: 56-83

[12] 白清源, 张兴娟, 杨春信. 锂/二氧化硫电池比热容的测量与分析[J]. 电子机械工程, 2011, 27(6): 1-3

BAI Q Y, ZHANG X J, YANG C X. Test and analysis of the specific heat capacity of lithium/sulfur dioxide battery[J]. Electro-Mechanical Engineering, 2011, 27(6): 1-3

[13] 郭赣. 真空热试验的温度测量系统[J]. 航天器环境工程, 2009, 26(1): 33-36

GUO G. Temperature measurement system for spacecraft thermal vacuum tests[J]. Spacecraft Environment Engineering, 2009, 26(1): 33-36

[14] 中国空间技术研究院. 航天器蓄电池比热容和放电时发热量测试方法: Q/W 1340—2012[S]

[15] 曾丹苓, 熬越, 张新铭, 等. 工程热力学[M]. 北京: 高等教育出版社, 2004: 49

（编辑：张艳艳）

A systematic measurement error analysis of heat generation of battery by discharging for spacecraft

WANG Yalong, SUN Tengfei, WANG Shuai, YANG Juhan, ZHU Qiyin

(Beijing Key Laboratory of Space Thermal Control Technology, Beijing Institute of Spacecraft System Engineering, Beijing 100094, China)

For the heat generation of battery by discharging, the measurement accuracy could affect the thermal control design and the work temperature of the battery in orbit directly. In this paper, the vacuum adiabatic measuremeat method is used to analyze the heat leak of the test system, and a revision model is developed. And the measurement errors of the heat generation from an analogue battery are studied, and the solutions to improve the measurement accuracy are proposed. The experimental results show that the measurement error is less than 6% when the power of the heat generation is between 2～25W and the discharging time is longer than 1h, and it decreases with the increase of the power. When the power is beyond 10W, the error is less than 3%, which meets the engineering requirements. It is meaningless to measure a mini-watt battery, whose absolute value of power of heat generation is less than 0.5W, since the measurement error will be relatively large yet.

battery for spacecraft; vacuum adiabatic measuremeat method; heat generation; system error

TM912; V416

A

1673-1379(2017)02-0207-07

10.3969/j.issn.1673-1379.2017.02.017

2016-08-09；

2017-03-20

王亚龙（1984—），男，硕士学位，主要从事航天器热控设计及试验技术研究。E-mail: wangyalong501@163.com。

http://www.bisee.ac.cn

E-mail: htqhjgc@126.com

Tel: (010)68116407, 68116408, 68116544