基于分频段加权的加速振动试验方法

朱学旺，张思箭，刘青林，农绍宁



基于分频段加权的加速振动试验方法

朱学旺，张思箭，刘青林，农绍宁

（中国工程物理研究院总体工程研究所，绵阳621999）

振动环境工程研究现行采用的加速试验方法中，都只考虑了加速因子与频率无关这种情形，这不仅提高了试验设备的推力要求，也增加了位移指标要求。文章提出了一种分频段加权的加速振动试验方法，即通过对低频段加速因子的权重的优化设计，实现较小的位移指标要求，且疲劳损伤累积等效。给出了基于Dirlik方法和TB方法疲劳损伤等效的加速试验设计方法和工程实现流程。针对该方法开展了应用实例的计算，结果表明：在疲劳损伤等效的前提下，显著降低了振动台的位移，且推力基本维持不变。

加速振动试验；疲劳损伤等效；分频段加权；疲劳损伤分析；Dirlik方法；TB方法

0 引言

基于疲劳损伤等效的加速试验方法常常用于装备的振动环境适应性研究，国内外主流标准都推荐了具体的加速振动试验方法。例如，美军标MIL- STD-810F/G[1-2]和我国军标GJB 150.16A[3]都给出了加速试验的等效关系式

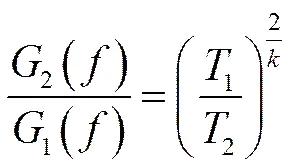
式中：1()、2()分别为原始试验条件和加速试验条件对应的功率谱密度；1、2分别为原始试验条件和加速试验条件对应的试验时间；为试验频率范围内的任意频率；为-曲线确定的材料常数之一，sN=。

这种加速试验方法的基本原理是基于疲劳损伤等效[4]，即通过提高试验条件量级和压缩试验时间来实现加速试验前、后被试产品（试验件）的疲劳损伤等效，广泛应用于各种产品的运输环境适应性研究[5-7]。分析式(1)不难发现，当确定了加速试验的时间压缩比(1/2)之后，以功率谱密度描述的加速试验条件在全频段范围内的任意频率上的加速比例（加速因子）是恒定的。这样做，至少要重点关注如下两个方面的限制：1）最低频率处能量的加速可能需要具有更大位移能力的试验设备，因为振动台的位移主要由低频条件确定[8]；2）试验件固有频率处附近的能量放大不能导致试验件发生非线性响应。

实际上，加速试验的疲劳损伤等效并没有对低频或试验件的固有频率处附近的试验条件量级有特别的要求，式(1)只是提供了实现加速试验疲劳损伤等效的方式之一。

本文提出另一种基于疲劳损伤等效的分频段加权加速试验方法，即通过构造加速因子随频率变化的功率谱密度，以实现低频试验条件和试验件固有频率处附近试验条件的优化设计。为了导出功率谱密度随频率变化的加速关系式，选择业界认定的与雨滴计数方法精度最为接近的疲劳损伤估计的两种频域方法[9-11]——Dirlik方法[12]和TB方法[13-14]，并应用疲劳损伤累积的线性模型（Palmgren-Miner模型），以获得加速试验条件确定的方法和步骤。

1 Dirlik方法和TB方法

针对宽带随机振动载荷的疲劳损伤分析，有多种频域估计方法可供选择[15-16]。本文提出的分频段加权加速试验方法采用Dirlik方法和TB方法以建立疲劳损伤等效关系。为方便计，先简单介绍这两种方法。

1.1 Dirlik方法[9,12]

Dirlik方法考虑了宽带随机振动的2个谱宽参数1、2对疲劳损伤累积的影响，将应力循环的幅值概率分布函数（PDF）描述为1个指数分布和2个Rayleigh分布的和，其PDF公式为

式中：=/σ，是循环幅值的标准化量；σ为载荷随机过程的总方均根值；1=2(12-22)/(1-22)；2=(1-2-1-12)/(1-)；3=1-1-2；=1.25× (2-3-2)，=(2-12-12)/(1-2-1+12)，其中1、2可以由随机过程的谱矩定义，即

。 (3)

值得注意的是，当载荷随机过程的功率谱密度为()时，σ就是式(3)描述的零阶矩阵。

于是，可以根据线性累积疲劳损伤的Palmgrem-Miner模型及材料的-曲线，估计出疲劳损伤率（单位时间的疲劳损伤）为

式中：v为随机载荷的峰值穿越率；、为-曲线确定的材料常数，sN=。

将式(2)代入式(4)，便得到Dirlik方法估计的宽带随机载荷的疲劳损伤率为

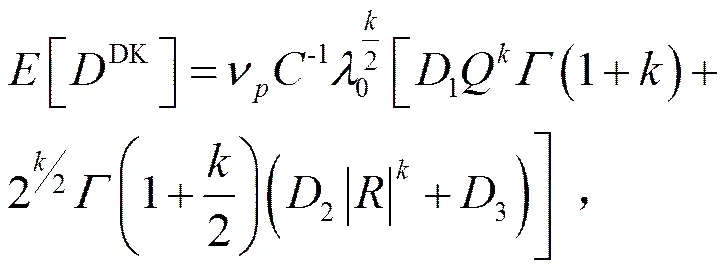
1.2 TB方法[13-14]

与Dirlik方法类似，TB方法分析宽带随机振动的疲劳损伤时也考虑了2个谱宽参数1、2对疲劳损伤累积的影响。直接给出TB方法公式：

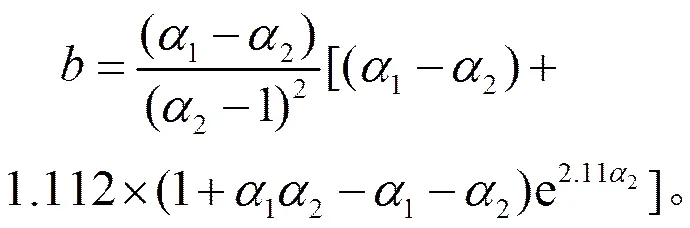
2 分频段加速试验条件设计

无论选择哪种方法分析随机振动的疲劳损伤，根据Palmgren-Miner模型，疲劳损伤等效公式都可以表示为

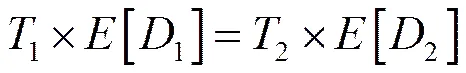
式中：为随机振动的作用时间；为疲劳损伤率，角标1、2分别代表加速前、后。

不难验证，当全频段具有相同的加速因子，即2()/1()=（为常数）对任意频率都成立时，选择Dirlik方法或TB方法进行疲劳损伤分析，其全部的模型参数如Dirlik模型的v、1、2、3、、和TB模型的v、2、等在振动加速前、后都具有相同的值。这样，时间压缩关系为

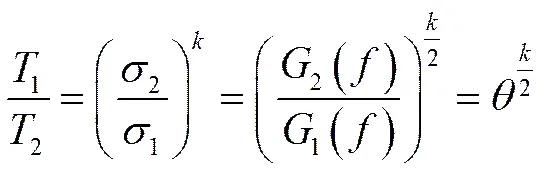
式中：1、2分别为加速前、后的随机振动1()、2()对应的总方均根值。式(9)正是式(1)描述的加速试验等效关系。

考虑分频段加速试验，此时以PSD之比定义的加速因子不再是常数，而是随频率变化的函数。选定一种疲劳损伤分析方法（如Dirlik方法或TB方法），应用式(8)可以获得分频段加速试验的通用等效关系。

为说明分析过程，以下假设为简单阶跃函数：

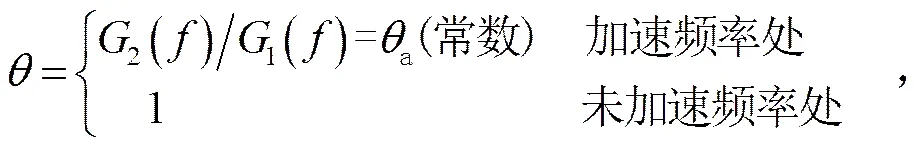
则加速试验条件2()的阶谱矩为

。 (11)

计

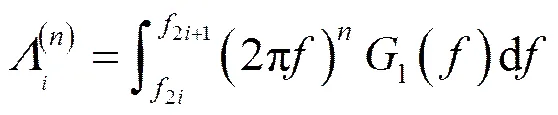
。 (13)

式(11)可简化为

其中为加速的频率段数，<。

这样，基于Dirlik方法和TB方法的分频段加速试验设计的步骤可归纳如下：

1）按式(3)计算未加速随机振动1()（作用时间1）的谱矩参数0、1、2、4，谱宽参数1、2和峰值穿越率ν。

2）根据需要加速的频段，计算未加速随机振动1()的阶谱矩分量。

3）给定加速因子a的初始值。

4）根据式(14)计算加速随机振动1()（作用时间2）的谱矩参数0、1、2、4，谱宽参数1、2和峰值穿越率ν。

5）针对加速前、后的随机振动分别计算模型参数。如选择Dirlik模型，则两组模型参数分别为1(1)、2(1)、3(1)、(1)、(1)和1(2)、2(2)、3(2)、(2)、(2)；如选择TB模型，则两个模型参数为1、2。

6）计算疲劳损伤比：

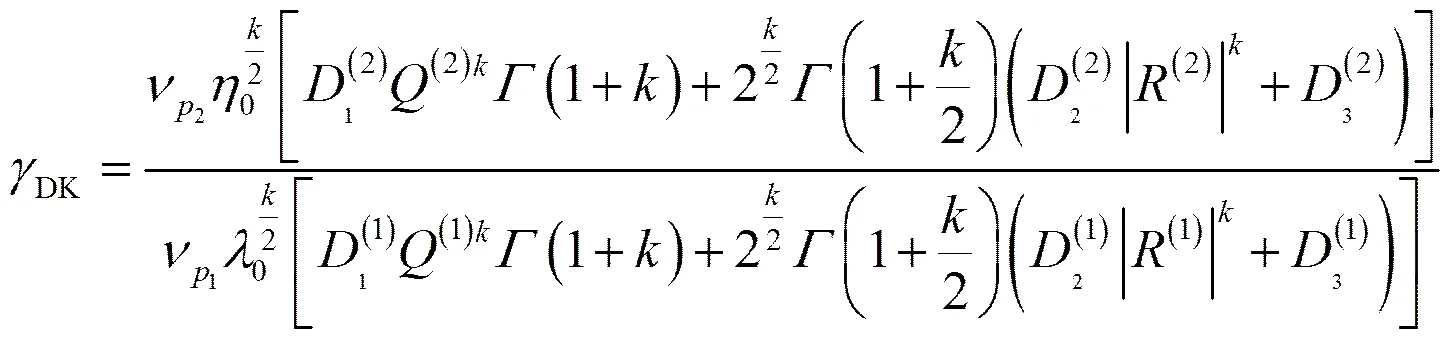
。(16)

7）根据给定的加速试验的时间压缩比进行加速因子均衡分析。若/2＞DK或/2＞TB，则应加大加速因子a的取值，重复步骤4）～步骤6）；若/2＞DK或/2＞TB，则应减小加速因子a的取值，重复步骤4）～步骤6）；均衡迭代的结束条件为/2≈DK或/2≈TB。

3 算例及讨论

1）算例1

以国军标GJB150.16A推荐的高速公路卡车运输条件为分析对象，设计分频段加速试验条件，并讨论其对设备能力的要求。如图1所示，1()为GJB150.16A推荐的高速公路卡车运输条件，试验1h相当行驶1600km。如果实际运输卡车速度为80km/h，则时间压缩比为20，这样可以导出未加速的卡车运输条件0()（材料常数为12时）。按照1～250Hz频段不加速，250～500Hz频段加速，时间压缩比不变，则基于TB方法的加速条件为2()，基于Dirlik方法的加速条件为3()。

图1 标准条件的分频段加速

注意到一个有趣的现象，图1中4个条件的总方均根值分别为0.861、1.106、1.110和1.059，这表明本文方法与标准推荐的方法相比，并没有增加对振动台的推力要求。但是按照标准推荐的方法进行加速试验，振动台的位移能力按照经验公式[8]计算约为130mm（峰-峰值），而采用本文方法进行高频段加速，位移仅需101mm，这对于试验的实施无疑是具有正面意义的。改变加速频段的起始频率，也会得出类似的结论。例如当加速起始频率为15Hz时，分频段的加速因子分别为1.77（TB方法）和1.76（Dirlik方法），对应的总方均根值分别为1.102和1.098。

2）算例2

图2中的a()为现场实测获得的某装备运输环境条件。按照时间压缩比为10设计加速试验条件，b()为标准推荐方法得出的结果（材料常数设为12），其加速因子在全频段均为1.468，总方均根值为0.966。采用本文方法分频段加速，加速频段为15～35Hz、55～200Hz，其他频段不加速，结果见图2中c()和d()，分频段放大因子分别为1.748（TB方法）和1.705（Dirlik方法），对应的总方均根值分别为0.962、0.966。不难计算，按照标准方法实施加速试验，位移要求是57mm（峰-峰值），而按照本文方法位移仅需要47mm，且对设备的推力要求基本相同。

如果试验前能够准确估计待试装备的共振频率区间，则可以有意识地将这一段频率设计为不加速，这样可以降低因为装备共振带来的非线性对试验构成的风险。算例中35～55Hz频段不加速便是基于这一考虑。

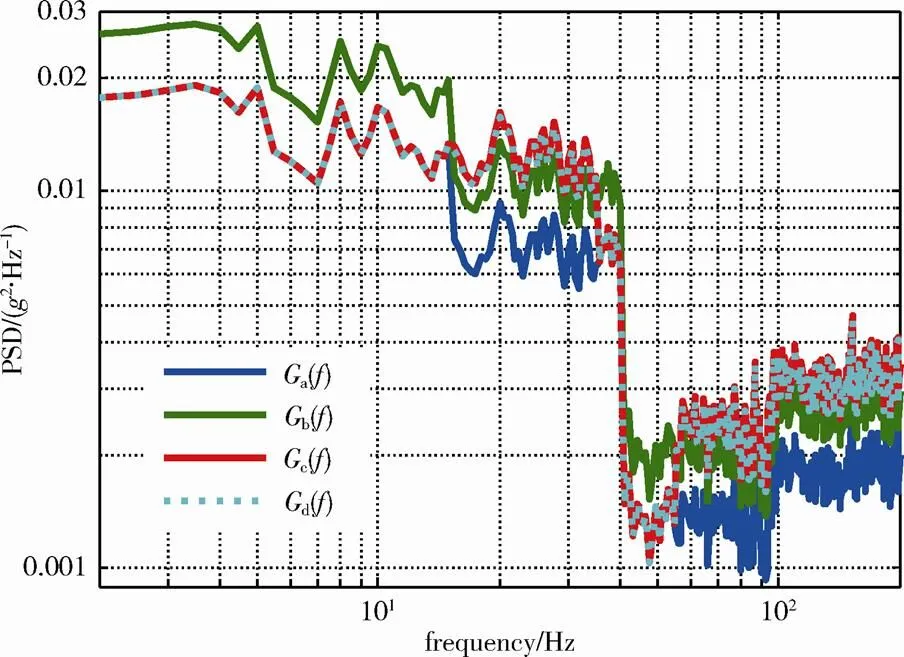
图2 实测条件的分频段加速

4 结束语

文章基于Dirlik方法和TB方法提出了一种分频段加权的加速振动试验方法，即通过控制低频段的加速因子的权重，实现了加速试验的疲劳损伤等效，且可以显著降低其对振动台的位移能力要求。两个算例既演示了本方法的应用过程，又验证了其有效性，结果表明不仅能实现加速试验的疲劳损伤等效，而且在不增加试验设备位移能力的前提下同样不增加对推力的要求。

本文仅针对加速频段的PSD放大因子相同这种简单工况进行了讨论；当需要对不同频段实施不一样的加速效果时，可以参照本方法进行加速试验的设计。

（References）

[1] Environmental engineering considerations and laboratory tests: Method 514.5 Vibration: MIL-STD-810F[S]

[2]Environmental engineering considerations and laboratory tests: Method 514.6 Vibration: MIL-STD-810G[S]

[3]军用装备实验室环境试验方法: 第16部分振动试验: GJB 150.16A－2009[S]

[4] 朱学旺. 疲劳损伤等效在随机振动试验中的应用[J]. 装备环境工程, 2007, 4(1): 11-13

ZHU X W. Application of fatigue damage equivalence in random vibration test[J]. Equipment Environmental Engineering, 2007, 4(1): 11-13

[5]POTHULA A, GUPTA A, KATHAWATE G R. Fatigue failure in random vibration and accelerated testing[J]. Journal of Vibration and Control, 2012, 18(8): 1199-1206

[6] SHIRES D. On the time compression (test acceleration) of broadband random vibration tests[J]. Packaging Technology and Science, 2011, 24: 75-87

[7] 朱学旺, 张思箭, 刘青林, 等. 包装产品公路运输环境模拟试验的加速因子[J]. 包装工程, 2014, 35(15): 44-47

ZHU X W, ZHANG S J, LIU Q L, et al. Discussions on the accelerated factor of highway transportation environmental test for packaged products in lab[J]. Packaging Engineering, 2014, 35(15): 44-47

[8] 胡志强, 法庆衍, 洪宝林, 等. 随机振动试验应用技术[M]. 北京: 中国计量出版社, 1996: 190

[9] BENASCIUTTI D, TOVO R.Comparison of spectral methods for fatigue analysis of broad-band Gaussian random processes[J]. Probabilistic Engineering Mechanics, 2006, 21: 287-299

[10] 曹明红, 邵闯, 齐丕骞. 宽带随机振动疲劳寿命的频域分析与试验对比研究[J]. 机械科学与技术, 2013, 32(6) : 839-844

CAO M H, SHAO C, QI P Q. Comparision of frequency domain analysis and the tests results for a wide-band random vibration fatique probiem[J]. Mechanical Science and Technology for Aerospace Engineering, 2013, 32(6): 839-844

[11] BOUYSSY V, NABOISHIKOV S M, RACKWITZ R. Comparison of analytical counting methods for Gaussian processes[J]. Struct Saf, 1993, 12: 35-57

[12] DIRLIK T. Application of computers in fatigue analysis[D]. UK: University of Warwich, 1985

[13] TOVO R. Cycle distribution and fatigue damage under broad-band random loading[J]. Int J Fatigue, 2002, 24(11): 37-47

[14] Benasciutti D, Tovo R. Spectral methods for lifetime prediction under wide-band stationary random processes[J]. Int J Fatigue, 2005, 27: 867-877

[15] 王冬梅, 谢劲松. 随机振动试验加速因子的计算方法[J]. 环境技术, 2010(2): 47-50

WANG D M, XIE J S. Acceleration factor calculation method of random vibration test[J]. Environmental Technology, 2010(2): 47-50

[16] 朱学旺, 张思箭, 宁佐贵, 等. 3准则应用对结构疲劳损伤评价的影响分析[J]. 航天器环境工程, 2014, 31(6): 609-613

ZHU X W, ZHANG S J, NING Z G, et al. Effects of 3clipping on the fatigue damage accumulation analysis result[J]. Spacecraft Environment Engineering, 2014, 31(6): 609-613

（编辑：肖福根）

An accelerated random testing procedure based on frequency band weighting approach

ZHU Xuewang, ZHANG Sijian, LIU Qinglin, NONG Shaoning

(Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621999, China)

The acceleration factor without consideration of the frequencies in the vibration engineering will require large displacements and forces for the shaker. A new accelerated random testing method is proposed based on the frequency band weighting and the required displacement for the shaker is less than that of the standard method due to the weighting factor design in the low frequency bands. A design procedure and an engineering scheme are developed according to two spectral models of the fatigue damage estimation, namely, the Dirlik model and the TB model. The numerical examples show that the proposed program can be used for the accelerated vibration testing design without large shaker displacement.

accelerated vibration testing; fatigue damage equivalent; frequency band weighting; fatigue damage estimation; Dirlik model; TB model

O324; O211

A

1673-1379(2017)02-0115-05

10.3969/j.issn.1673-1379.2017.02.001

2017-01-13；

2017-03-12

朱学旺（1963—），男，研究员，长期从事复杂结构动力学及振动环境试验研究。E-mail: x.w.zhu@163.com。

http://www.bisee.ac.cn

E-mail: htqhjgc@126.com

Tel: (010)68116407, 68116408, 68116544