配准误差下的多基地雷达目标检测算法

胡勤振 苏洪涛 刘子威 周生华 杨 阳



配准误差下的多基地雷达目标检测算法

胡勤振 苏洪涛*刘子威 周生华 杨 阳

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071);(西安电子科技大学信息感知技术协同创新中心 西安 710071)

在多基地雷达系统中，即使进行了空间配准处理，也很难实现完美的空间配准。该文研究了分布式MIMO雷达系统存在配准误差时的目标检测问题。根据是否利用已知先验配准误差信息对目标位置信息进行估计，给出了MAP-GLRT和ML-GLRT两种检测器。由于MAP-GLRT检测器利用了先验信息，因此其检测性能优于ML-GLRT检测器。在配准误差条件下，两种检测器的性能要优于传统的融合检测算法。通过仿真实验验证了所提算法的有效性。

多基地雷达；配准误差；目标检测

1 引言

在分布式多输入多输出(Multiple-Input Multiple-Output, MIMO)雷达系统中，发射站和接收站在空间上分散布置，利用目标的空间散射特性可以得到空间分集增益，从而提高目标检测性能。各个发射站发射正交信号，接收站通过与发射信号对应的匹配滤波器组得到对应的回波信号，因此每一对发射站和接收站构成一个空间分集通道。在传统的融合检测算法中，假设空间是完全配准的，即在将各接收站的观测转换到公共坐标系的过程中不存在配准误差，根据搜索空间中的检测区域可以准确搜索到各空间分集通道中需要融合的回波数据。然而在实际工程应用中，由于存在雷达站址误差、测距误差和时间误差，不同雷达站照射到目标的时间也不一定相同。特别是对于机载雷达、弹载雷达、舰载雷达等运动平台，在进行协同探测时，很难满足空间完全配准条件。

针对分布式雷达系统的配准误差校正，目前已经提出了大量的配准算法，主要包括基于测量级的配准算法和基于跟踪级的配准算法。虽然这些算法能够很好地校正未知非随机的系统偏差，由于还存在随机的测量误差，因此不能完全消除配准误差。另外，在配准误差校正之后的观测中，随机测量误差仍然会影响雷达系统中回波数据在公共坐标系中的转换。因此，即使进行了系统的配准误差校正，在公共坐标系中，各空间分集通道仍然会存在比较小的空间配准误差。由于配准误差的影响，在公共坐标系中，待检测目标会出现在一个包含多个采样点的不确定区域内。而传统的融合检测方法在融合各空间分集通道中的观测时，认为空间是完全配准的，因此会将含有期望目标的回波信号与不含有期望目标的回波信号进行融合，从而导致信噪比损失，降低空间分集增益，造成检测性能的下降[14]。文献[15,16]考虑了在有限观测集合下的目标检测问题，在每个空间分集通道中，从连续多个空间采样中估计出目标回波延时，并给出似然比检测算法，然而，不足之处是没有考虑空间配准误差分布情况。

到目前为止，针对空间未配准条件下的分布式MIMO雷达目标检测问题的研究相对较少，文献[17]给出了信噪比已知时的未配置信号融合算法，考虑到在各空间分集通道中，目标会出现在一个不确定区域内，在进行采样后，为一有限观测集合。本文研究了存在空间配准误差时且信噪比未知时的目标检测问题。首先利用最大后验估计方法估计出每个空间分集通道中期望目标回波信号幅度。然后，根据相应的配准方法，当各空间分集通道中目标在不确定区域内的概率分布先验已知时，利用最大后验估计方法估计出每个空间分集通道中期望目标回波信号所在的位置，然后将估计值代入似然函数中，得到似然比检验统计量。当配准误差的概率分布未知时，则认为服从均匀分布，此时给出虚警概率的显式表达式。为说明所提算法的有效性，在实验仿真中，比较了在配准误差条件下所提算法与传统融合检测算法的检测性能，分析了不同配准误差对检测器检测性能影响。

2 配准误差信号模型

假设分布式MIMO雷达系统具有空间分散布置的t个发射天线和r个接收天线。发射天线和接收天线的空间位置分别为和。每组发射天线和接收天线构成一组空间分集通道。目标服从Swerling I模型，其空间位置为。发射天线发射时长为，带宽为的正交波形信号，并满足：

(3)

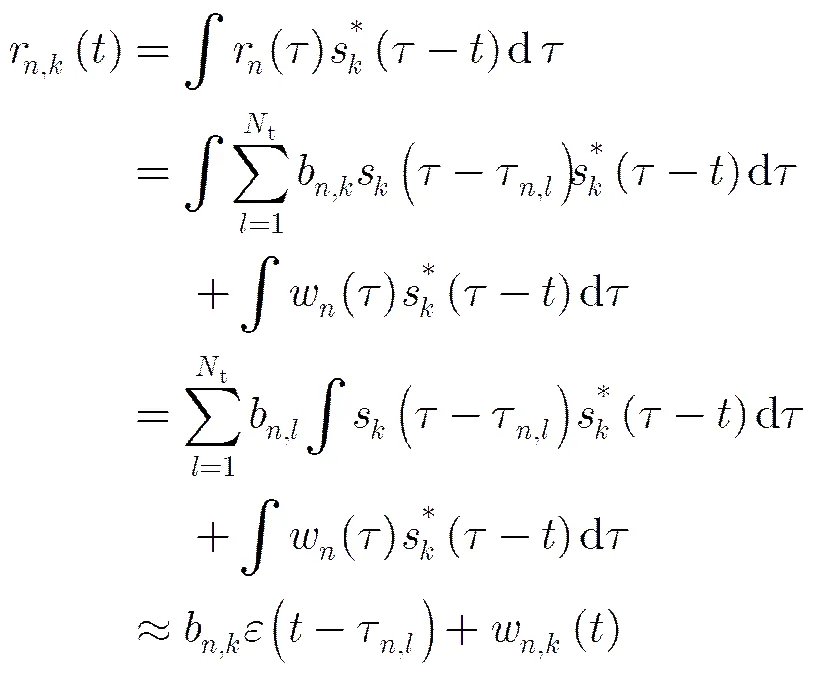
在传统的检测融合算法分析中，常常假设各空间分集通道是空间配准的，因此根据空间检测区域，得到不同空间分集通道的时延，进行信号融合检测。然而在实际应用中，即使进行了空间配准处理，仍然会存在一定的空间配准误差。此时，在每个空间分集通道中，目标会出现在一个不确定区域内。参考文献[2]，空间分辨单元的尺寸为，针对每个空间分辨单元进行采样，则该不确定区域内，可得到有限观测集合。

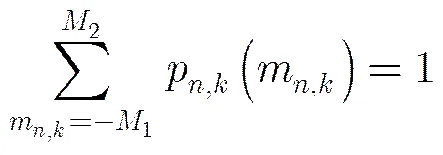
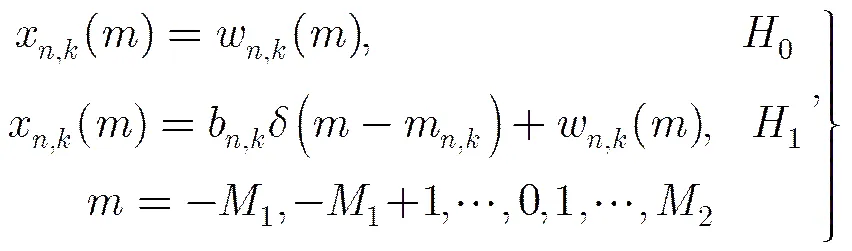
(7)

和

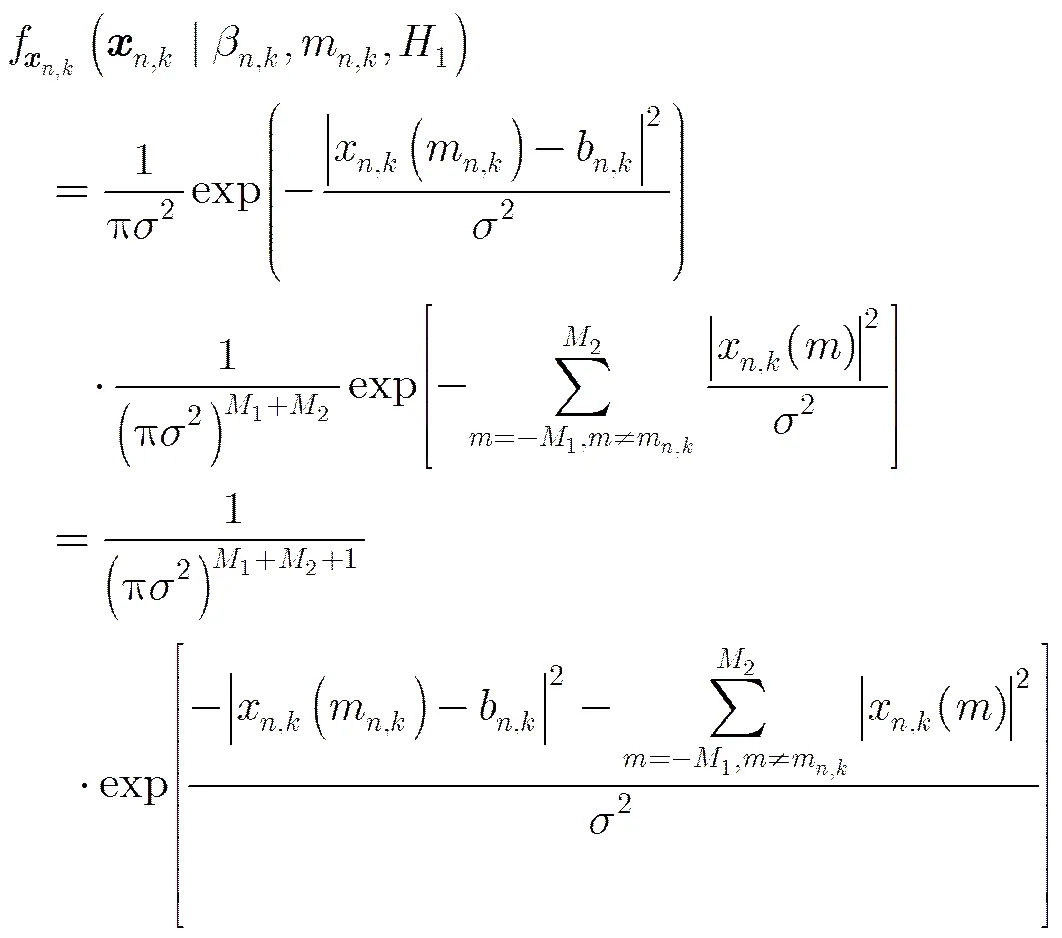
(9)

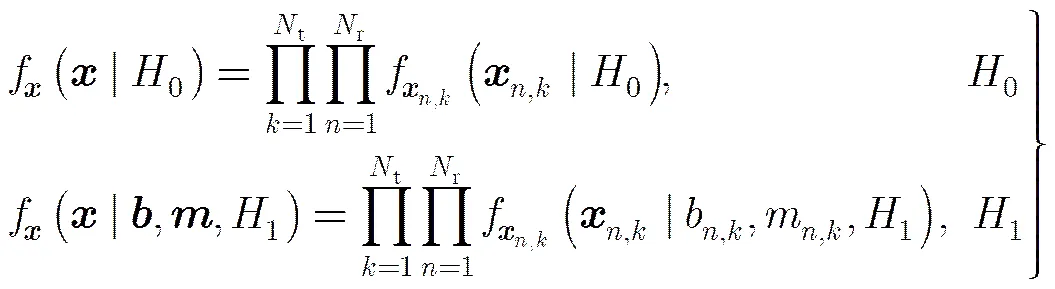
3 检测器设计

在分析配准误差下的目标检测问题中，需要考虑的未知参数为目标信号复幅度和目标回波位置。广义似然比检验(Generalized Likelihood Ratio Test, GLRT)是对概率密度函数中的含有未知参数时常用的检测方法，是似然比检验的次优检测方法。本文采用GLRT判决准则，对未知的目标信号复幅度进行最大似然(Maximum Likelihood, ML)估计得到。若已知的先验概率分布，对未知的目标回波位置进行最大后验(Maximum A Posteriori, MAP)估计得到；若未知先验信息，则认为服从均匀分布，对未知的目标回波位置进行ML估计得到。根据目标回波位置的MAP估计和ML估计，则对应两种GLRT检测器：MAP-GLRT和ML-GLRT。

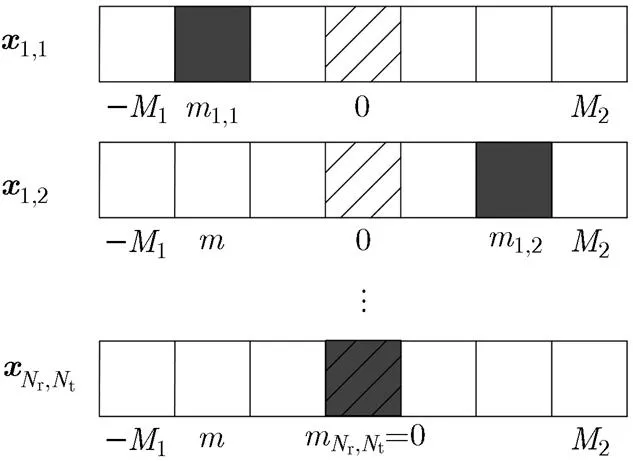
图1存在配准差时的有限观测集合模型

3.1 MAP-GLRT检测器

在已知配准误差概率分布的情况下，MAP- GLRT检测器可以表示为

(12)

我们有

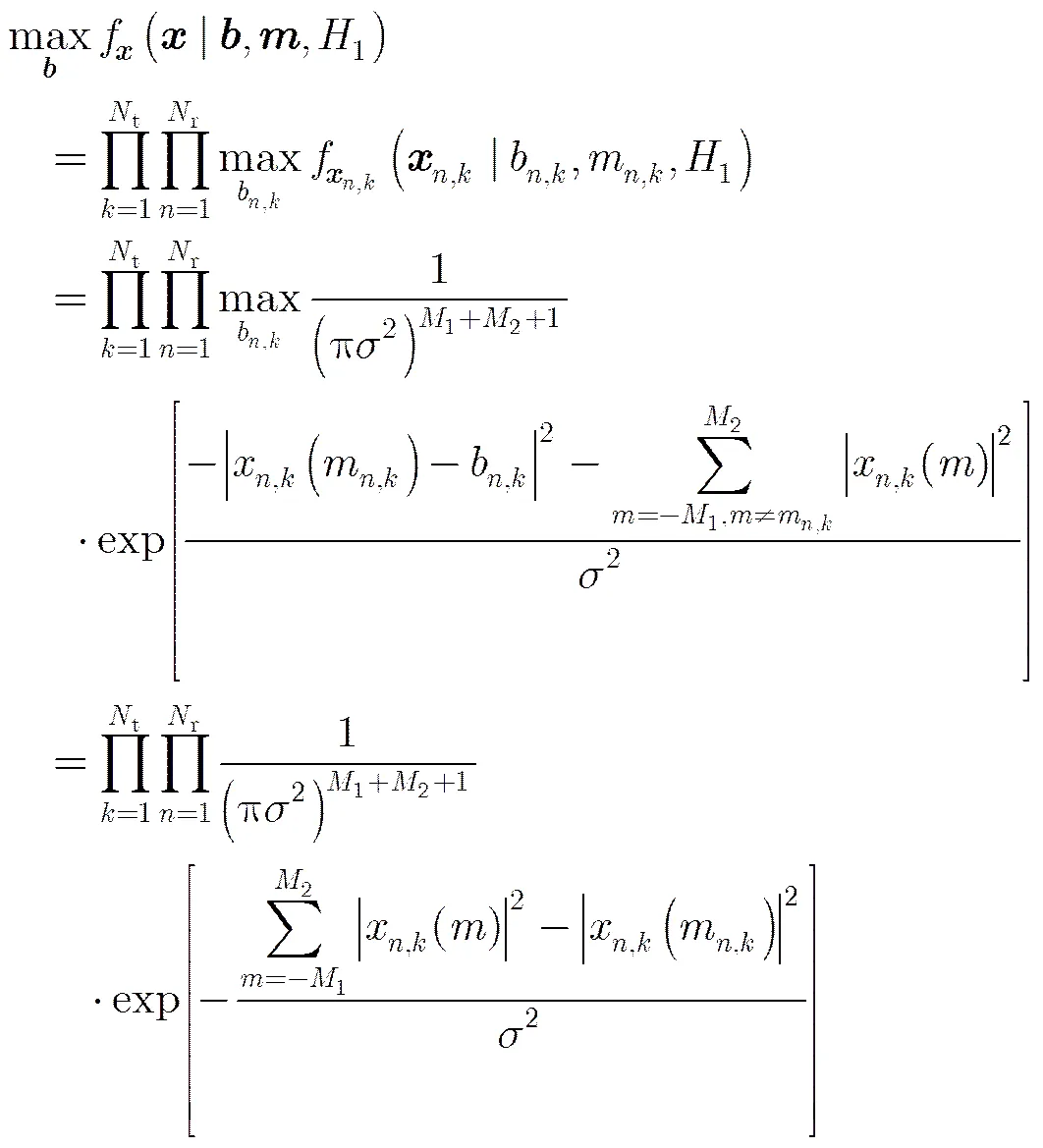
将式(13)代入式(14)可得

(15)

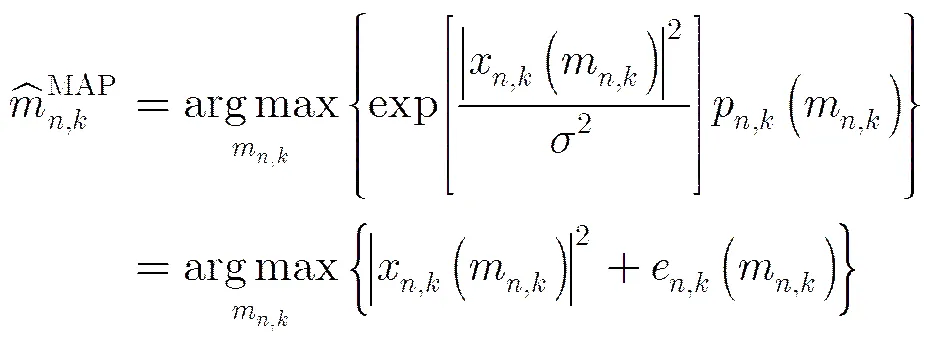
将式(16)代入式(11)，可得广义似然比为

经过化简，最终的MAP-GLRT检测器可以表示为

(18)

3.2 ML-GLRT检测器

在未知配准误差概率分布的情况下，ML-GLRT检测器可以表示为

(20)

可得

(22)

经过简化，最终的ML-GLRT检测器可以表示为

(25)

(27)

由于两种检测器都是对目标幅度进行了ML估计，因此两种检测器都适应于信噪比未知的环境。同时两种检测器都需要知道不确定区域的大小。当配准误差分布未知时，无法使用MAP-GLRT检测器，但可以使用ML-GLRT检测器。由于MAP- GLRT检测器利用了先验信息，因此可以得到比ML-GLRT检测器更好的检测性能。

4 仿真实验

图3给出了ML-GLRT检测器的虚警概率理论值和Monte Carlo仿真值对比。图中，Monte Carlo试验次数为107次，空间通道数为6。从图中可以看出，在不同的配准误差下，式(26)的理论推导与Monte Carle仿真结果基本吻合，因此可以说明理论推导的正确性。

图4给出了不同的配准误差大小对各个检测性能的影响，图4(a)和图4(b)中，空间通道数分别为4和6，通道信噪比设置分别为8 dB和7 dB。图中，最优检测性能为假设空间完美配准条件下得到的，单基地雷达检测概率也不涉及到空间配准问题，因此二者的检测概率曲线与配准误差大小没有关系。从图中可以看出，随着配准误差的增大，传统的LRT检测器，MAP-GLRT检测器和ML-GLRT检测器的检测概率逐渐降低，MAP-GLRT检测器优于传统的LRT检测器和ML-GLRT检测器，原因是MAP- GLRT检测器利用了配准误差的先验信息。还可以看出，在配准误差较小的情况下，传统的LRT检测器优于ML-GLRT检测器，但随着配准误差的增大，传统的LRT检测器性能损失加快，低于ML-GLRT检测器性能。对于两种提出的检测算法，当配准误差标准差大于一定值时，其检测性能要低于单基地雷达系统。

图5给出了不同配准误差下，MAP-GLRT检测器和ML-GLRT检测器的检测概率随SNR的变化。图4(a)和图4(b)中，空间通道数分别为4和6。从图中可以看出，当配准误差标准偏差时，MAP-GLRT检测器性能与传统LRT检测器性能相似，并接近于最优检测器性能，而ML-GLRT检测器有1 dB的信噪比损失。当配准误差标准偏差时，MAP-GLRT检测器和ML-GLRT检测器相比于最优检测器，有2~4 dB的性能损失，但是在高信噪比条件下，仍然可以获得比单基地雷达更好的检测性能。而传统的似然比检测器的性能损失较大，且低于单基地雷达系统的检测性能。可以看出，配准误差会严重降低信号融合的检测性能，所提两种检测算法虽然在一定程度上可以改善检测性能，但在较大的配准误差下，仍然会有较大的性能损失。

图3 ML-GLRT检测器的虚警概率理论值和仿真值对比 图4 检测性能随配准误差变化

图5 检测性能曲线

5 结论

在多基地雷达系统中，即使进行了空间配准处理，也很难实现完美的空间配准。本文研究了分布式MIMO雷达系统存在配准误差时的目标检测问题。针对配准误差导致多基地雷达传统的LRT检测器性能损失，提出了MAP-GLRT和ML-GLRT两种检测器，分别用MAP估计和ML估计方法对目标的空间位置估计，由于MAP-GLRT利用了先验配准误差信息，因此其检测性能优于ML-GLRT。在存在配准误差的情况下，两种检测器的性能会优于传统的似然比检测器。仿真实验验证了所提算法的有效性。

[1] Liu Jun, Li Hongbin, and HIMED B. Persymmetric adaptive target detection with distributed MIMO radar[J]., 2015, 51(1): 372-382. doi: 10.1109/TAES.2014.130652.

[2] Haimovich A, Blum R, Cimini L,MIMO radar with widely separated antennas[J]., 2008, 25(1): 116-129. doi: 10.1109/MSP.2008. 4408448.

[3] Frankford M T, Stewart K B, Majurec N,Numerical and experimental studies of target detection with MIMO radar[J]., 2014, 50(2): 1569-1577. doi: 10.1109/ TAES.2014.120180.

[4] 金镇, 谢良贵, 文树梁. 分布式MIMO雷达单脉冲测角[J]. 雷达学报, 2014, 3(4): 474-479. doi: 10.3724/SP.J.1300.2014. 13077.

JIN Z, XIE L G, and WEN S L. Distributed MIMO radar monopulse angular estimation[J]., 2014, 3(4): 474-479. doi: 10.3724/SP.J.1300.2014.13077.

[5] LI Hongbin, WANG Zhe, LIU Jun,Moving target detection in distributed MIMO radar on moving platforms[J]., 2015, 9(8): 1524-1535. doi: 10.1109/JSTSP.2015.2467355.

[6] Radmard M, Chitgarha M M, Majd M N,Antenna placement and power allocation optimization in MIMO radar detection[J]., 2014, 50(2): 1468-1478. doi: 10.1109/ TAES.2014.120776.

[7] Liu Hongwei, Zhou Shenghua, Su Hongtao,Detection performance of spatial-frequency diversity MIMO radar[J]., 2014, 50(4): 3137-3155. doi: 10.1109/TAES.2013.120040.

[8] HU Qinzhen, SU Hongtao, ZHOU Shenghua,Two-stage constant false alarm rate detection for distributed multiple- input multiple-out radar[J].,&, 2016, 10(2): 264-271. doi: 10.1049/iet-rsn.2015.0026.

[9] Zhou Y F and Leung H. An exact maximum likelihood registration algorithm for data fusion[J]., 1997, 45(6): 1560-1572. doi: 10.1109/ 78.599998.

[10] Okello N and Ristic B. Maximum likelihood registration for multiple dissimilar sensors[J]., 2003, 39(3): 1074-1083. doi: 10.1109/TAES.2003.1238759.

[11] Huang D L, Leung H, and Bosse E. A pseudo- measurement approach to simultaneous registration and track fusion[J]., 2012, 48(3): 2315-2331. doi: 10.1109/ TAES.2012.6237594.

[12] Ristic B, Clark D, and Gordon N. Calibration of multi-target tracking algorithms using non-cooperative targets[J]., 2013, 7(3): 390-398. doi: 10.1109/TSTSP.2013. 2256877.

[13] HAO Mengxi, YUAN Xianghui, and HAN Chongzhao. Recursive joint track-to-track association and sensor nonlinear bias estimation based on generalized Bayes risk[C]. 18th International Conference on Information Fusion, Washington, DC, 2015: 1519-1525.

[14] Thomopoulos S and Okello N. Distributed and centralized multisensor detection with misaligned sensors[J]., 1994, 77(1): 293-323. doi: 10.1016/ 0020-0255(94)9006-X.

[15] Tajer A, Jajamovich G H, Wang X D,Optimal joint target detection and parameter estimation by MIMO radar[J]., 2010, 4(1): 127-145. doi: 10.1109/TSTSP.2010. 2040104.

[16] Moustakidex G V, Jajamovich G H, Tajer A,Joint detection and estimation: optimum tests and applications[J]., 2012, 58(7): 4215-4229. doi: 10.1109/TIT.2012.2184260.

[17] HU Qinzhen, SU Hongtao, ZHOU Shenghua,. Target detection in distributed MIMO radar with registration errors[J]., 2016, 52(1): 438-450. doi: 10.1109/TAES.2015. 140479.

[18] Bhargava R and Khatri C. The distribution of product of independent beta random variables with application to multivariate analysis[J]., 1981, 33(1): 287-296. doi: 10.1007/ BF02480942.

胡勤振： 男，1988年生，博士生，研究方向为雷达目标检测、统计信号处理.

苏洪涛： 男，1974年生，教授，研究方向为自适应信号处理、超视距雷达信号处理.

刘子威： 男，1989年生，博士生，研究方向为雷达抗干扰技术、超视距雷达信号处理.

Target Detection Algorithm for Multistatic Radar with Registration Errors

HU Qinzhen SU Hongtao LIU Ziwei ZHOU Shenghua YANG Yang

(,,’710071,);(,,’710071,)

In a multistatic radar system, perfect registration is unavailable in practice even after a registration process. In this paper, a target detection problem for a distributed Multiple-Input Multiple-Output (MIMO) radar with registration errors is considered. To estimate target positions by weather using a knowinginformation of registration errors or not, a MaximumGeneralized Likelihood Ratio Test (MAP-GLRT) detector and a Maximum Likelihood GLRT (ML-GLRT) detector are proposed. The MAP-GLRT detector outperforms the ML-GLRT detector due to the prior information. The two proposed algorithms have better detection performance over the conventional detection fusion algorithm with registration errors. Simulation results verify the effectiveness of the proposed detection algorithms.

Multistatic radar; Registration errors; Target detection

TN957.51

A

1009-5896(2017)01-0088-07

10.11999/JEIT160207

2016-03-07；改回日期：2016-07-12；

2016-10-09

苏洪涛 suht@xidian.edu.cn

国家自然科学基金(61372134, 61401329)

The National Natural Science Foundation of China (61372134, 61401329)