基于MATLAB的腔体滤波器耦合矩阵诊断调试

姚 远，谢 晓，高 雅，曹 亮



基于MATLAB的腔体滤波器耦合矩阵诊断调试

姚 远，谢 晓，高 雅，曹 亮

（中国电子科技集团公司第26研究所，重庆 400060）

根据柯西法提取耦合系数，结合遗传优化算法构建滤波器耦合矩阵的诊断模型，并在Matlab中编程实现了腔体带通滤波器的诊断。通过诊断即从仿真或测试的滤波器参数中提取的耦合矩阵，与综合的理想耦合矩阵进行比较，对滤波器下一步调谐的方向和幅度进行指导。以一个七阶交叉耦合腔体滤波器的研制为例，通过Matlab与HFSS联合仿真，诊断优化后的回波损耗满足预期指标，验证了该诊断方法的有效性。

腔体滤波器；耦合矩阵；参数提取；柯西法；协同仿真；滤波器诊断

腔体滤波器因其具有损耗低、承受功率高等特点，在各种电子系统中具有广泛的应用。特别是国内一些通信设备厂家在移动基站和直放站等系统中对腔体滤波器的需求较大，促进了滤波器的设计、制造技术的发展。因而对腔体滤波器设计技术的研究，无论从理论上还是从实际应用方面讲，都是非常有意义的，并可带来一定的经济价值。

腔体滤波器的设计离不开调谐，而滤波器的计算机辅助诊断调试技术为实际的调试工作带来极大方便。诊断的过程即为：从测试或仿真的参数(散射参数)中提取耦合矩阵，通过对比提取的耦合矩阵与综合出的理想耦合矩阵之间的差异，可以知道哪一部分是造成滤波器响应未达到设计要求的主要因素，从而指导滤波器的下一步调谐。诊断调试技术可以加快滤波器的调谐过程进而缩短滤波器的生产和研发周期，成为目前研究的一个热点。

1 诊断的基本原理及步骤

在一个无耗的滤波器电路模型中，输入输出端口处没有引入传输线。但在实际的滤波器模型中需要考虑三个非理想因数：(1) 输入输出传输线引入的参数相位加载；(2) 高阶模引起的相位加载；(3) 每个谐振腔的损耗。为了消除这三个影响诊断结果的因素，本文通过五参数优化方法移除仿真或测试参数的相移效应，而采用频域归一化修正变换公式移除滤波器的损耗因素。然后使用柯西法确定相移移除后的仿真或测试参数的特征多项式和，最后耦合矩阵通过参数得到，并使用已有的技术[1-2]将得到的横向耦合矩阵简化为实际物理拓扑的耦合矩阵。

1.1 五参数法与遗传优化算法结合移除相位效应

定义5个未知的参数01，01，02，02和u，其中01和02分别是输入输出端口处的相位加载，01和02分别是输入输出端在中心频率0处的等效电长度，每个谐振腔具有相同的无载值，为u。

这5个未知参数可以使用遗传算法优化目标函数（式1）求得。遗传算法（GA）使用类似于生物进化的过程，通过对代的选择、交叉、重插入等操作，选择全局最优的解，用于求解目标函数的最大或最小值。

1.2 求解多项式，和的系数

散射参数11、21可由三个特征多项式，和近似，建立有理多项式模型如式(3)[3-4]所示：

由于柯西法[3-4]通常要求被取样数据为无耗的，因此通过从带通频域归一化到低通频域′的频率修正的变换公式（4），假定每个谐振腔具有相同的无载u，则滤波器的损耗因素被移除，计算出的，和多项式在域是无耗的。

从滤波器的仿真结果或实测响应中取个频率点，建立方程组求解多项式的系数、，方程组用矩阵表示如下：

为滤波器的阶数，为传输零点的个数，m为范德蒙矩阵，其元素为

式（5）的解通过对矩阵使用奇异值分解获得，在Matlab中则为调用svd函数。在滤波器的相位加载被移除，同时损耗因素消除后，由svd函数求解出多项式()()的系数，最后根据Feldkeller方程计算出()。

1.3 耦合矩阵的提取

滤波器的综合与诊断调试理论均统一于耦合矩阵。从已知滤波器测得参数中提取能够反映实际腔体结构和频响之间关系的耦合矩阵，即为滤波器的诊断[5-7]。从已知的响应曲线中取样，继而构建多项式模型，求出滤波器的传输和反射函数，最后得到耦合矩阵。当前响应对应的耦合矩阵求出后，与理论综合的标准矩阵比较，即可确定滤波器调试的方向与幅度。

由传输函数21和反射函数11的多项式，和，求出对应的导纳参数[Y]，将网络导纳矩阵进行部分分式展开，即可得到极点和对应的留数：和。导纳参数[Y]用留数矩阵形式可表示为：

由等效电路法综合滤波网络的导纳函数[Y]，可以表示为：

联立两个方程式，可得出

由于本文采用非完全规范的滤波函数的拓扑结构，即源和负载之间无耦合，因此取0=0。

由此滤波网络的横向耦合矩阵则全部求解出来。然后用已有技术将横向耦合矩阵，进行一系列相似变换化简为实际物理实现的拓扑结构形式。

2 诊断对调谐的指导及应用实例

耦合结构腔体带通滤波器的设计和实现步骤主要包括以下四步：

（1）根据滤波器设计指标，选择滤波器拓扑结构，综合耦合矩阵，记为﹡；

（2）选择谐振腔类型，在电磁仿真软件（如HFSS）中建立单腔、双腔仿真模型并对物理尺寸进行参数扫描，根据﹡以及扫描结果确定滤波器的初始尺寸参数，仿真得到参数；

（3）利用仿真参数以及Matlab代码实现的第二节中算法对滤波器进行诊断，提取耦合矩阵记为，比较和﹡值，得到调谐的方向与幅度。通过重复“仿真→诊断→调谐”这一优化过程，该过程为Matlab代码控制HFSS自动执行，即协同仿真，最后得到所需的频率响应。

（4）由于实际加工等因素对滤波器性能的影响，在测试过程中对滤波器加入调谐螺钉等方式进行调谐。通过重复“测试→诊断→调谐”这一调谐过程直到获得所需的频率响应。

本文以七阶腔体带通滤波器设计为实例，验证了上文中的诊断方法对调谐过程的指导作用。

该七阶滤波器指标要求如下：

通带损耗：1 785~1 805 MHz <2 dB

回波损耗：1 785~1 805 MHz <–15 dB

衰减：1 710~1 770 MHz >50 dB

1 820~1 898 MHz >25 dB

采用Caneron的分析法[8-9]综合出不包含源与负载耦合的+2阶耦合矩阵，并利用相似变换技术变换到一个适合于实现的拓扑结构的耦合矩阵，即为标准耦合矩阵﹡。

表1 标准耦合矩阵（对角线已转化为谐振腔频率）

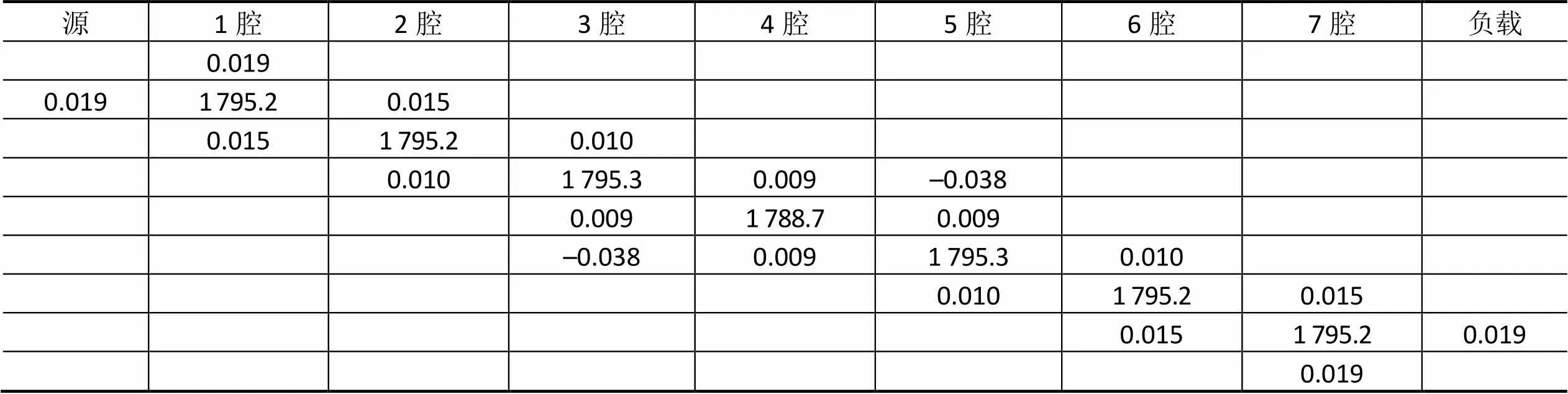
Tab.1 Standard coupling matrix (diagonal element converted to frequency)

在HFSS中建立仿真模型（图1），通过Matlab和HFSS协同仿真优化后仿真所得参数如图2所示，通带内反射小于–15 dB。诊断提取的耦合矩阵应尽量与标准耦合矩阵相同。

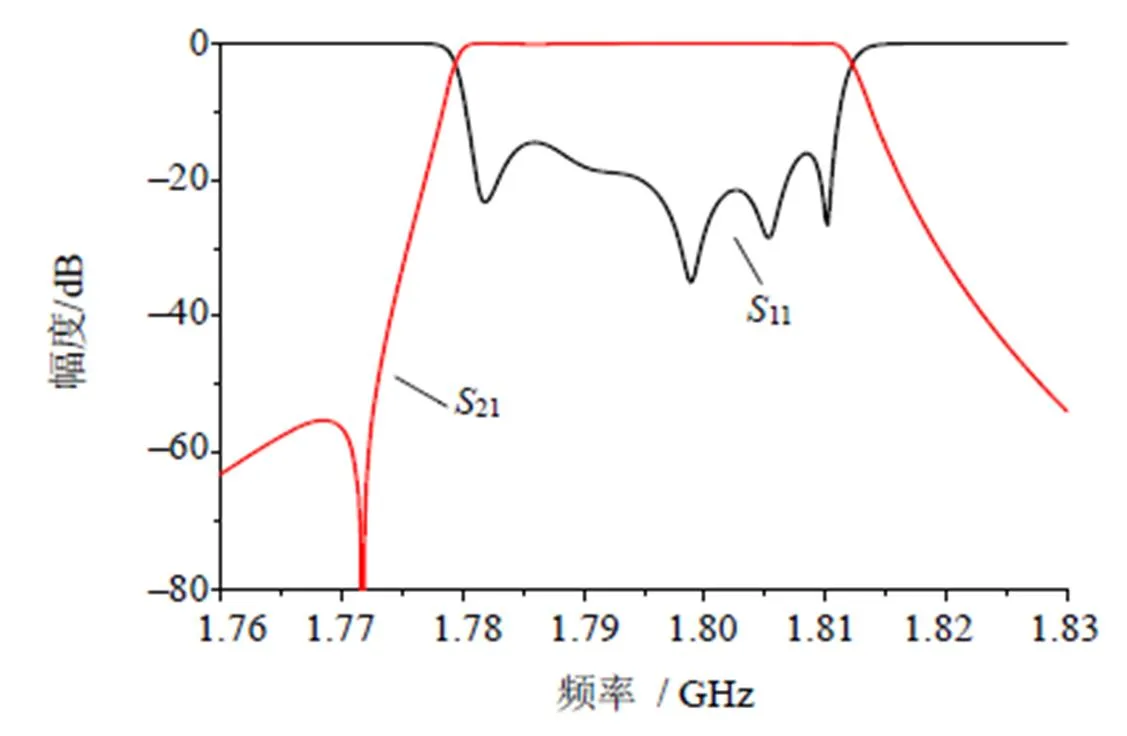
图2 优化后仿真的S参数

图3是经实际加工制作后实测的参数，与仿真曲线非常相似。通过前述方法从实测参数中提取耦合矩阵并与标准耦合矩阵﹡对比，它们之间的差异如表2所示。由于交叉耦合35腔系数相差略大（见表2），导致最终测试曲线传输零点没有计算曲线的传输零点尖锐。腔2的频率比目标值偏差1 MHz，所以通带中回波损耗在1.8 GHz附近与图2中标准曲线有一些差别。此外12腔，56腔耦合系数较标准值大，所以实测曲线也比标准曲线带宽略宽。

表2 实测提取参数与标准耦合矩阵（表1）的差异

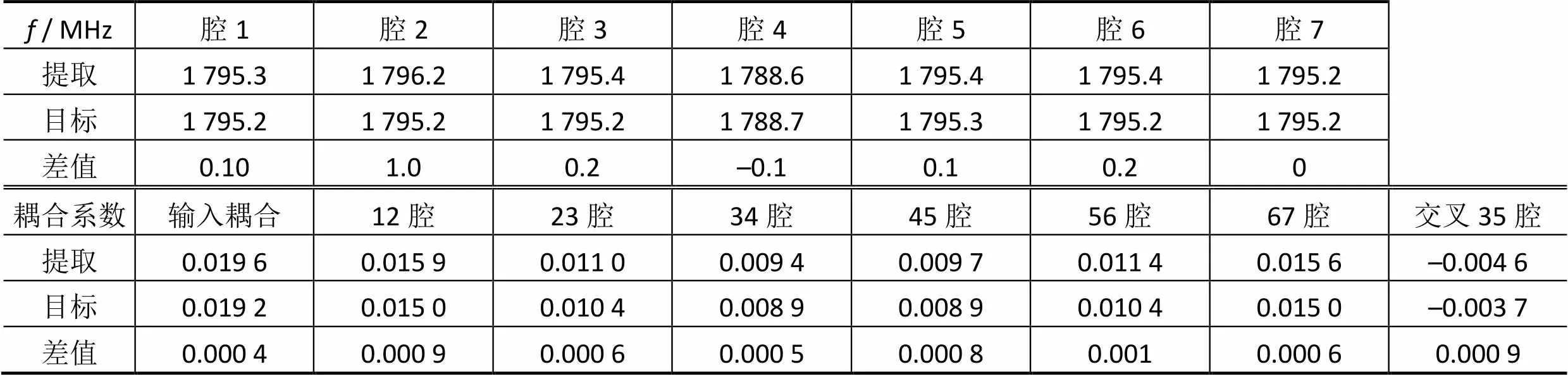
Tab.2 Differences between standard coupling martix(Tab.1) and coupling matrix extracted from measurement

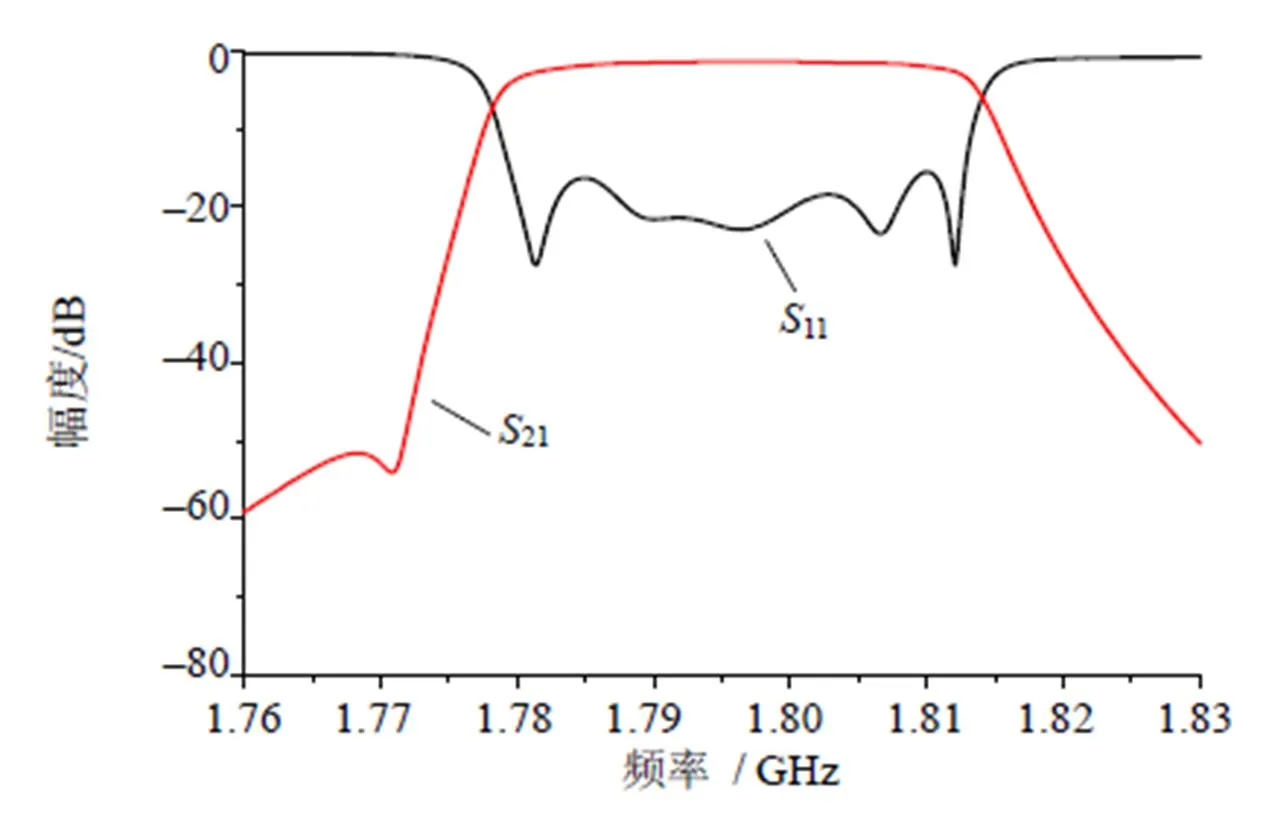
图3 滤波器实物测试曲线

3 结论

本文采用五参数优化方法，移除仿真或测试参数的相移效应并获得每个谐振腔的无载值（本文假设每个腔有相同的无载值）（并通过频域归一化修正变换公式，移除滤波器的损耗因素），然后使用柯西法确定相移移除后的仿真或测试参数的特征多项式，和，最后耦合矩阵通过参数得到，并使用已有的技术将得到的横向耦合矩阵简化为实际物理拓扑的耦合矩阵。通过对比提取的耦合矩阵与根据指标综合出的耦合矩阵之间的差异，进而明确下一步滤波器调谐的方向和幅度。

[1] 韩世虎, 王锡良, 樊勇. 广义切比雪夫滤波器耦合矩阵的优化提取 [J]. 电波科学学报, 2007, 22(1): 153-157.

[2] 李忻, 聂在平. 交叉耦合模型及其在腔体滤波器中的实现 [J]. 电子科技大学学报, 2004, 33(4): 354-367.

[3] 陈佳, 陈建忠, 赖鑫, 等. 腔体滤波器计算机辅助诊断与调谐 [C]// 2009年全国微波毫米波会议论文集（下册）. 西安: 中国电子学会, 2009: 1714-1717.

[4] 王瑞. 微波无源器件综合与诊断技术研究[D]. 成都: 电子科技大学, 2012.

[5] 张永亮. 微波无源器件综合新技术及其计算机辅助调试的研究 [D]. 西安: 西安电子科技大学, 2013.

[6] 韩应宾, 赵永久, 路宏敏. 微波滤波器的耦合矩阵诊断调试法 [J]. 西安电子科技大学学报(自然科学版), 2008, 35(4): 703-706.

[7] 张永亮, 苏涛, 吴边, 等. 改进柯西法的多工器有理模型的提取方法 [J]. 西安电子科技大学学报(自然科学版), 2013, 40(3): 201-204.

[8] CAMERON R J. Advanced coupling matrix synthesis techniques for microwave filters [J]. IEEE Trans Microwave Theory Tech, 2003, 51(1): 1-10.

[9] CAMERON R J. General coupling matric synthesis methods for Chebyshev filtering function [J]. IEEE Trans Microwave Theory Tech, 1999, 47(4): 433-442.

（编辑：陈丰）

Diagnosis and debugging of cavity filter coupling matrix based on Matlab

YAO Yuan, XIE Xiao, GAO Ya , CAO Liang

(CETC No.26 Research Institute, Chongqing 400060, China)

The coupling coefficient was extracted by Cauchy method. Combined with genetic algorithm, the diagnosis model of coupling matrix was constructed, and the diagnosis programs (Matlab codes) of the cavity band-pass filter were developed. The coupling matrix was extracted from the simulated or testedparameters of the filter, and then compared with the ideal coupling matrix. The differences between two matrixes gave the direction and amplitude of the next tuning of the filter. Taking the development of a 7 order cavity filter as an example, Matlab and HFSS co-simulation were carried out. After the simulation and optimization process, the return loss meets the expected target, and the validity of the method is verified.

cavity filter; coupling matrix; parameter extraction; Cauchy method; co-simulation; diagnosis of filter

10.14106/j.cnki.1001-2028.2017.01.008

TN713

A

1001-2028（2017）01-0044-04

2016-11-04

姚远

姚远（1981－），男，重庆人，高级工程师，主要从事声表面波滤波器、谐振器及声表传感器设计开发，E-mail: Xibeifeiying@foxmail.com 。

http://www.cnki.net/kcms/detail/51.1241.TN.20161230.1018.008.html

网络出版时间：2016-12-30 10:18:57